2.4 自由落体运动—【新教材】人教版(2019)高中物理必修第一册同步练习
文档属性
| 名称 | 2.4 自由落体运动—【新教材】人教版(2019)高中物理必修第一册同步练习 |  | |
| 格式 | doc | ||
| 文件大小 | 936.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-18 14:48:27 | ||
图片预览




文档简介
2.4
自由落体运动(同步练习)
1.(2020春?阳江期末)据说,当年牛顿躺在树下被一个从树上掉下的苹果砸中,从而激发灵感发现了万有引力定律。若苹果以的速度砸中牛顿头部,不计空气阻力,取重力加速度大小,则该苹果下落前距牛顿头部的高度为
A.
B.
C.
D.
2.(2020秋?辽阳月考)在研究力和运动的关系时,伽利略提出了著名的理想实验,示意图如图所示。伽利略提出该理想实验是为了说明
A.物体运动不需要力来维持
B.力可以改变物体的运动
C.物体运动时就会产生惯性
D.力是维持物体运动的原因
3.(2020春?渝中区校级期末)如图所示,小球甲从空中的点静止释放,下落了时,小球乙从点下方处的点静止释放,经历一段时间后,两个小球同时落地(不计空气阻力),则点离地高度为
A.
B.
C.
D.
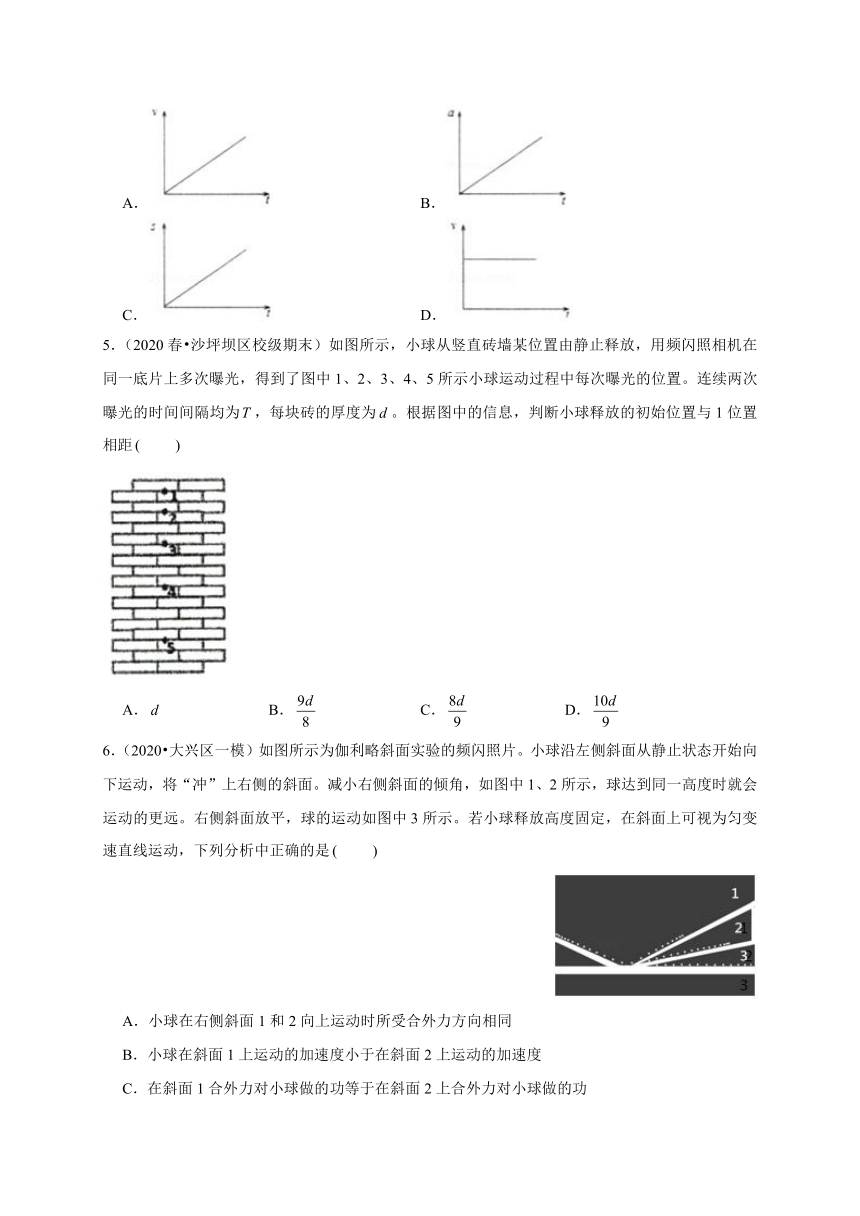
4.(2020春?温州期末)一个苹果从树上无初速度地自由下落,将苹果看成质点,忽略空气阻力,取向下为正方向。设苹果下落过程中的速度为、加速度为、位移为、下落时间为,则下列描述各物理量与时间变化图象中正确的是
A.
B.
C.
D.
5.(2020春?沙坪坝区校级期末)如图所示,小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5所示小球运动过程中每次曝光的位置。连续两次曝光的时间间隔均为,每块砖的厚度为。根据图中的信息,判断小球释放的初始位置与1位置相距
A.
B.
C.
D.
6.(2020?大兴区一模)如图所示为伽利略斜面实验的频闪照片。小球沿左侧斜面从静止状态开始向下运动,将“冲”上右侧的斜面。减小右侧斜面的倾角,如图中1、2所示,球达到同一高度时就会运动的更远。右侧斜面放平,球的运动如图中3所示。若小球释放高度固定,在斜面上可视为匀变速直线运动,下列分析中正确的是
A.小球在右侧斜面1和2向上运动时所受合外力方向相同
B.小球在斜面1上运动的加速度小于在斜面2上运动的加速度
C.在斜面1合外力对小球做的功等于在斜面2上合外力对小球做的功
D.因为在水平面上小球受到向前的冲力,所以小球在水平面3上运动的更远
7.(2020春?锦州期末)一小球自高处自由下落,当它与水平地面每碰撞一次后,速度大小减小为碰撞前的,不计空气阻力,取,则下列说法正确的是
A.第一次下落的时间与第二次下落的时间之比为
B.第二次弹起的高度为第一次弹起时高度的
C.小球运动的总时间约为
D.小球运动的总位移为
8.(2019秋?连云港期末)伽利略为了研究自由落体运动的规律,将落体实验转化为“斜面实验”,对于这个研究过程下列说法正确的是
A.“斜面实验”冲淡了重力作用,便于测量时间
B.“斜面实验”“放大”了重力作用,便于测量位移
C.“斜面实验”可以直接得到自由落体运动规律
D.伽利略对自由落体运动的研究,是科学实验和逻辑推理的完美结合
9.(2020春?金安区校级月考)如图所示,在足够高的空间内,小球位于空心管的正上方处,空心管长为,小球的球心与管的轴线重合,并在竖直线上,小球直径小于管的内径,不计空气阻力,则下列判断正确的是
A.两者均无初速度同时释放,小球在空中能过空心管
B.小球自由下落、管固定不动,小球穿过管的时间
C.小球自由下落、管固定不动,小球穿过管的时间
D.两者均无初速度释放,但小球提前△时间释放,则小球穿过管的时间
10.(2019秋?剑川县校级期末)已知月球表面附近的重力加速度是地球表面的重力加速度的,先后分别在月球和地球表面上高处释放一个小球,空气阻力不计时,下列说法正确的是
A.在月球和地球上小球的下落快慢是一样
B.在月球和地球上小球的速度比为
C.小球在月球和地球上的落地时的速度之比为
D.小球在月球和地球上的落地时间之比为
三.填空题(共4小题)
11.(2020春?浦东新区校级期中)从某一高度相隔先后释放两个相同的小球,不计空气阻力,它们在空中任一时刻的间距 (选填“越来越大”、“越来越小”、“保持不变”
,速度之差 (选填“越来越大”、“越来越小”、“保持不变”
。
12.(2019?吉林学业考试)小萌同学在塔楼顶部由静止释放一铅球,已知该塔楼高度为,重力加速度取.若忽略空气阻力,铅球在空中运动时间为 ;落地时速度为 。
13.(2019秋?荔湾区校级月考)一物体作自由落体运动,经过3秒物体落地,则它在最后内下落的高度是 ;物体在下落的第内、第内、第内的平均速度之比是 。取;
14.(2019春?南昌期末)利用水滴下落可以测出重力加速度,调节水龙头,让水一滴一滴地流出,在水龙头的正下方放一个盘子,调整盘子的高度,使一水滴刚碰到盘子时,恰好有另一水滴从水龙头开始下落,而空中还有3个正在下落的水滴。测出水龙头到盘子间的距离为。再用秒表测时间,从第一滴水滴离开水龙头开始计时,到第滴水滴落到盘中,共用时间为。
(1)当第一滴水滴落到盘中时,第二滴水滴离开水龙头的距离为 ;
(2)测得的重力加速度为 。
15.(2020春?祁门县校级期中)某自来水管的管口定时滴下水滴,现在管口的正下方放置以金属盘,水滴滴到盘上发出响声,逐渐向上平移金属盘直到看见水滴从管口刚好滴出时,恰好听到水滴滴到盘底的响声,记录盘底的高度,再继续上移盘,第二次,第三次看见水从管口滴出同时听到水滴落到盘底的响声,分别测出盘底离地面的高度和,实验测得,,,.求:
(1)相邻水滴滴出的时间间隔;
(2)自来水管的管口离地面的高度。
16.(2020春?濂溪区校级月考)如图所示,竖直悬挂一根长的直杆,在杆的正下方距离杆下端观察点处有一内径大于杆的直径的圆环。求:
(1)当杆做自由落体运动,直杆全部通过处环所需的时间。
(2)当直杆开始自由下落的瞬间,将环以竖直向上抛出,求直杆全部通过环所需的时间。取,杆和环距离地面足够高,杆的一端进入到另一端离开为通过)
17.(2019秋?常德期末)如图所示,某同学测出一棵苹果树树干部分的高度约为,一个苹果从树冠顶端的树梢上由于受到扰动而自由下落,该同学测出苹果经过树干所用的时间为,重力加速度取,则:
(1)苹果树树冠部分的高度约为多少?
(2)苹果落地时的速度为多大?
18.(2019秋?上月考)一根轻质细线将2个薄铁垫圈、(大小可忽略)连接起来,、间细线长为,距地面一定高度,放手后、自由下落,若、落地时间相差,,求:
(1)距地面的高度;
(2)落地时的速度。
19.(2019春?蓝田县期中)如图所示,悬挂着的一根长为的直杆,在直杆正下方处有一个无底圆筒,若将悬线剪断,直杆通过圆筒所用的时间为,,求:
(1)无底圆筒的长度;
(2)直杆下端穿过圆筒所用的时间是多少?(计算结果保留根号)
答案
1、【分析】苹果做自由落体运动,根据求该苹果下落前距牛顿头部的高度。
【解答】解:根据得:
因当年牛顿躺在树下,那么苹果下落前距牛顿头部的高度为,故正确,错误。
故选:。
2、【分析】本题考查了伽利略斜面实验的物理意义,明确伽利略通过“理想斜面实验”推翻了力是维持运动的原因的错误观点。
【解答】解:亚里士多德认为,力是维持物体运动的原因;伽利略等人认为,力是改变物体运动状态的原因。现在人们普遍认为力是改变物体运动状态的原因的观点是正确的;
而伽利略设计这个理想实验,其目的是为了说明亚里士多德的力是维持物体运动状态的原因的结论是错误的,物体运动不需要力来维持,故错误,正确。
故选:。
3、【分析】小球甲乙分别做自由落体运动,求得甲乙下落的时间,根据同时落体即可求得小球甲的高度。
【解答】解:设小球甲距地面的高度为,下落的时间为,则,解得
小球甲下落所需时间为,则,解得
小球乙下落的时间为,则,解得
联立解得:,故错误,正确;
故选:。
4、【分析】物体做自由落体运动的条件:①只在重力作用下;②从静止开始。只在重力作用下保证了物体的加速度为;从静止开始保证了物体初速度等于零。所以自由落体运动是初速度为0的匀加速直线运动。
【解答】解:、自由落体运动的速度,速度与时间成正比,故正确,错误;
、自由落体运动的加速度为重力加速度,是不变的,故错误;
、位移为,与的图象为过原点的抛物线,故错误。
故选:。
5、【分析】已知小球在连续相等的时间内位移,运用位移差公式和平均速度公式可求出加速度及某点的瞬时速度,再根据速度与位移关系求位移,进而求解。
【解答】解:小球由2到3和1到2的位移差,得;
小球到2点的瞬时速度;
设小球下落点到2点距离,由得,;
小球释放的初始位置与1位置,故正确;
故选:。
6、【分析】根据小球在斜面上的运动情况分析合外力方向关系;根据牛顿第二定律分析在斜面1和斜面2上加速度的大小;根据动能定理确定合外力对小球做的功大小;结合惯性概念分析小球在水平面3上运动的原因。
【解答】解:、小球在右侧斜面1和2向上都做匀减速运动,合外力方向均沿斜面向下,知合外力方向不同,故错误;
、设任一斜面的倾角为,根据牛顿第二定律得,得,所以,小球在斜面1上运动的加速度大于在斜面2上运动的加速度,故错误;
、根据动能定理知,合外力对小球做的功等于小球动能的变化量,而小球动能的变化量相等,所以在斜面1合外力对小球做的功等于在斜面2上合外力对小球做的功,故正确;
、在水平面上小球不受向前的冲力,由于惯性,所以小球在水平面3上运动的更远,故错误。
故选:。
7、【分析】设小球第一次落地时速度为,进而可表示出,,,,根据速度时间关系求解时间之比;
根据速度位移关系求解位移之比;
归纳出小球从开始下落到第次与地面相碰经过时间,根据等比数列前项和公式求解时间;
根据位移的概念求解位移。
【解答】解:、设小球第一次落地时速度为,则有
那么第二次、第三次、第次落地速度分别为,,,
根据速度时间关系可得:
则小球第一次下落的时间与第二次下落的时间之比为:,故正确;
、小球开始下落到第一次与地相碰经过的路程为
小球第一次与地相碰后弹起的高度是:
小球第二次与地相碰后弹起的高度是,则
所以第二次弹起的高度与第一次弹起时高度之比为:,
所以第二次弹起的高度为第一次弹起时高度的,故错误;
、小球第1下落时间为:
小球从第1次与地面相撞到第2次与地面相撞经过的时间为:
小球从第2次与地面相撞到第3次与地面相撞经过的时间为:
小球从第次与地面相撞到第次与地面相撞经过的时间为:
所以小球运动的总时间为:
代入数据解得:,故正确;
、小球最终静止在地面上,所以整个过程中小球运动的总位移为,方向向下,故正确。
故选:。
8、【分析】本题考查了有伽利略“斜面实验”的知识,根据其历史背景我们知道,之所以采用“斜面实验”,注意碍于当时对时间的测量技术、手段落后。
【解答】解:、伽利略时代,没有先进的测量手段和工具,为了“减小”重力作用,采用斜面实验,其实就是为了使物体下落时间长些,便于时间的测量,减小实验误差,故正确,错误;
、根据实验结果,伽利略将实验结论进行合理的外推,得到落体的运动规律,但不能进行直接的计算,故错误;
、伽利略根据实验结果,伽利略将实验结论进行合理的外推,得到落体的运动规律,是科学实验和逻辑推理的完美结合,故正确;
故选:。
9、【分析】根据位移关系可知,要使小球穿过空心管,则小球的位移应比空心管的位移多,根据匀变速直线运动的位移时间公式列式求解小球穿过空心管所用的时间。
若两者无初速度同时释放,则两者都做自由落体运动,小球在空中不能穿过空心管。
【解答】解:、若两者无初速度同时释放,则两者都做自由落体运动,在相同时间内下降的高度相同,可知小球在空中不能穿过空心管,故错误;
、若小球自由下落、管固定不动,小球穿过管的时间是小球到达管的下端与到达管的上端的时间差,根据自由落体运动公式可知:,故错误,正确;
、两者均无初速度释放,但小球提前△时间释放,以管为参考系,小球相对管匀速运动,则有:△,,可知小球穿过管的时间:,故正确。
故选:。
10、【分析】根据加速度大小比较下落快慢,由加速度和自由落体规律求得小球的速度比和落地时间比。
【解答】解:、由为在地球上重力加速度大,故在地球自由下落时和月球上下落时快慢程度不一样,故错误;
、根据自由落体运动规律可知,落地速度可知,落地速度在高度相同的情况下与重力加速度的平方根据成正比,故错误,正确;
、根据自由落体运动规律可知,下落所用时间,下落时间在下落高度相同的情况下与重力加速度的平方根成反比,故正确。
故选:。
11、【分析】两球均做自由落体运动,由速度时间公式求出速度之差与时间的关系式。
【解答】解:两球做自由落体运动,加速度都为重力加速度;以释放第二球开始计时,第一球的速度,经过时间后,第一球的速度,第二球的速度,则两球的速度差为:△。两球的速度之差保持不变。
此后先释放的小球的位移为:
后释放的小球的位移为::
它们之间的距离差为:△
可知它们的间距越来越大
故答案为:越来越大;保持不变
12、【分析】铅球做自由落体运动,由位移公式和速度公式可求解。
【解答】解:铅球做自由落体运动,由位移公式得:
铅球在空中运动时间:
由速度公式得:
故答案为:3,30
13、【分析】自由落体运动是初速度为0的匀加速直线运动,在开始通过连续相等时间内的位移比为,连续相等位移的时间比为,根据求解平均速度。由此分析即可。
【解答】解:根据,内的位移为:
内的位移为:
所以第内的位移为:
根据匀变速直线运动的导出公式可知第内、第内、第内的时间之比为:
根据平均速度公式可得:
故答案为:25,
14、【分析】(1)当一滴水碰到盘子时,恰好有另一滴水从水龙头开始下落,而空中还有3个正在下落的水滴,知水滴将分成时间相等的4份,根据初速度为0的匀加速运动,在相等时间内的位移比为,求出第二滴水离盘子的高度。
(2)从第一滴水离开水龙头开始,到第滴水落至盘中,共用时间为,知道两滴水间的时间间隔,根据求出重力加速度。
【解答】解:(1)由题意可知,水滴将分成时间相等的4份,4份相等时间内位移比为,
总高度为,所以第二滴水滴离水龙头的高度为:,
故第二个水滴离开水龙头的距离为。
(2)从第一滴水离开水龙头开始,到第滴水落至盘中(即滴水离开水龙头),共用时间为,
知道两滴水间的时间间隔为:,
根据得:
解得:
故答案为:,。
15、【分析】(1)水滴做的是自由落体运动,根据△,可以计算时间将的大小;
(2)利用平均速度的关系可以求得第二次时瞬时速度的大小,再计算下降的高度。
【解答】解:(1)设相邻水滴的时间间隔为,由题:
,,
由匀变速直线运动的导出公式:,
解得:
(2)利用公式求得:,
故水管口离第二次小水滴位置的高度:,
因此自来水水管离地面的高度:
答:(1)相邻水滴出的时间间隔为;
(2)自来水水管口离地面的高度为。
16、【分析】(1)杆全部通过点的距离为,根据位移公式可求速度;杆全部通过点需时间为杆的上端到达点的时间减去杆的下端到达点的时间,根据自由落体位移时间公式即可求解;
(2)二者都运动时,分别求出杆与环相遇的时间与分离的时间,然后求出差即可。
【解答】解:(1)根据自由落体位移公式:①
得到下落时间公式:②
杆下端到达点所经过的位移:,代入②式解得③
杆上端到达点所经过的位移:,代入②式解得④
杆通过点所需的时间为:△⑤
(2)将环以竖直向上抛出,杆与环相遇的时间为,则:⑥
杆与环分离的时间为,则:⑦
直杆全部通过环所需的时间:△⑧
联立可得:△⑨
答:(1)当杆做自由落体运动,直杆全部通过处环所需的时间是。
(2)直杆全部通过环所需的时间也是。
17、【分析】设开始下落到达树干的时间为,结合位移关系列式,从而根据位移时间公式求出物体开始下落时树冠的高度,根据求出末速度。
【解答】解:设开始下落到达树干的上沿的时间为,有:
△
代入数据解得:。
则:。
苹果落地的速度为:
答:(1)苹果树树冠部分的高度约为
(2)苹果落地时的速度为。
18、【分析】(1)根据自由落体运动的位移时间公式分别求出两球下落的时间,然后结合两球落地的时间差求出距地面的高度;
(2)结合速度时间公式求出球落地时球的速度。
【解答】解:(1)由匀变速直线运动的位移公式得:①
②
又:△③
④
代入数据解得:,;
(2)球落地的时间与运动的时间相等,此时球的速度为:⑤
代入数据可得:。
答:(1)距地面的高度是;
(2)落地时的速度为。
19、【分析】(1)直杆做的是自由落体运动,根据自由落体运动的规律可以求得下降时杆的速度的大小,再由位移公式可以求得在内杆下降的距离,此距离即为杆和圆筒的总长度的大小;
(2)直杆下端穿过圆筒所用的时间是从杆点落到筒端开始,到杆的端落到端结束,结合位移时间公式进行求解。
【解答】解:取杆的下端点为研究对象,
设下降时点的速度的大小为,根据可得:
直杆通过圆筒的时间是从点进入圆筒开始,到点离开圆筒时结束,
设杆长为,圆筒的长度为,则在内杆下降的距离为,
由位移公式可得:,
解得:,
(2)到时间为,则:
到的时间为,则:
直杆下端穿过圆筒所用时间为:△
联立解得:
答:(1)无底圆筒的长度为;
(2)直杆下端穿过圆筒所用的时间是
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/10/13
0:33:47;用户:梦青;邮箱:orFmNt3xQq6ez0-hcFH4Sf27Af1M@weixin.m;学号:38022509
自由落体运动(同步练习)
1.(2020春?阳江期末)据说,当年牛顿躺在树下被一个从树上掉下的苹果砸中,从而激发灵感发现了万有引力定律。若苹果以的速度砸中牛顿头部,不计空气阻力,取重力加速度大小,则该苹果下落前距牛顿头部的高度为
A.
B.
C.
D.
2.(2020秋?辽阳月考)在研究力和运动的关系时,伽利略提出了著名的理想实验,示意图如图所示。伽利略提出该理想实验是为了说明
A.物体运动不需要力来维持
B.力可以改变物体的运动
C.物体运动时就会产生惯性
D.力是维持物体运动的原因
3.(2020春?渝中区校级期末)如图所示,小球甲从空中的点静止释放,下落了时,小球乙从点下方处的点静止释放,经历一段时间后,两个小球同时落地(不计空气阻力),则点离地高度为
A.
B.
C.
D.
4.(2020春?温州期末)一个苹果从树上无初速度地自由下落,将苹果看成质点,忽略空气阻力,取向下为正方向。设苹果下落过程中的速度为、加速度为、位移为、下落时间为,则下列描述各物理量与时间变化图象中正确的是
A.
B.
C.
D.
5.(2020春?沙坪坝区校级期末)如图所示,小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5所示小球运动过程中每次曝光的位置。连续两次曝光的时间间隔均为,每块砖的厚度为。根据图中的信息,判断小球释放的初始位置与1位置相距
A.
B.
C.
D.
6.(2020?大兴区一模)如图所示为伽利略斜面实验的频闪照片。小球沿左侧斜面从静止状态开始向下运动,将“冲”上右侧的斜面。减小右侧斜面的倾角,如图中1、2所示,球达到同一高度时就会运动的更远。右侧斜面放平,球的运动如图中3所示。若小球释放高度固定,在斜面上可视为匀变速直线运动,下列分析中正确的是
A.小球在右侧斜面1和2向上运动时所受合外力方向相同
B.小球在斜面1上运动的加速度小于在斜面2上运动的加速度
C.在斜面1合外力对小球做的功等于在斜面2上合外力对小球做的功
D.因为在水平面上小球受到向前的冲力,所以小球在水平面3上运动的更远
7.(2020春?锦州期末)一小球自高处自由下落,当它与水平地面每碰撞一次后,速度大小减小为碰撞前的,不计空气阻力,取,则下列说法正确的是
A.第一次下落的时间与第二次下落的时间之比为
B.第二次弹起的高度为第一次弹起时高度的
C.小球运动的总时间约为
D.小球运动的总位移为
8.(2019秋?连云港期末)伽利略为了研究自由落体运动的规律,将落体实验转化为“斜面实验”,对于这个研究过程下列说法正确的是
A.“斜面实验”冲淡了重力作用,便于测量时间
B.“斜面实验”“放大”了重力作用,便于测量位移
C.“斜面实验”可以直接得到自由落体运动规律
D.伽利略对自由落体运动的研究,是科学实验和逻辑推理的完美结合
9.(2020春?金安区校级月考)如图所示,在足够高的空间内,小球位于空心管的正上方处,空心管长为,小球的球心与管的轴线重合,并在竖直线上,小球直径小于管的内径,不计空气阻力,则下列判断正确的是
A.两者均无初速度同时释放,小球在空中能过空心管
B.小球自由下落、管固定不动,小球穿过管的时间
C.小球自由下落、管固定不动,小球穿过管的时间
D.两者均无初速度释放,但小球提前△时间释放,则小球穿过管的时间
10.(2019秋?剑川县校级期末)已知月球表面附近的重力加速度是地球表面的重力加速度的,先后分别在月球和地球表面上高处释放一个小球,空气阻力不计时,下列说法正确的是
A.在月球和地球上小球的下落快慢是一样
B.在月球和地球上小球的速度比为
C.小球在月球和地球上的落地时的速度之比为
D.小球在月球和地球上的落地时间之比为
三.填空题(共4小题)
11.(2020春?浦东新区校级期中)从某一高度相隔先后释放两个相同的小球,不计空气阻力,它们在空中任一时刻的间距 (选填“越来越大”、“越来越小”、“保持不变”
,速度之差 (选填“越来越大”、“越来越小”、“保持不变”
。
12.(2019?吉林学业考试)小萌同学在塔楼顶部由静止释放一铅球,已知该塔楼高度为,重力加速度取.若忽略空气阻力,铅球在空中运动时间为 ;落地时速度为 。
13.(2019秋?荔湾区校级月考)一物体作自由落体运动,经过3秒物体落地,则它在最后内下落的高度是 ;物体在下落的第内、第内、第内的平均速度之比是 。取;
14.(2019春?南昌期末)利用水滴下落可以测出重力加速度,调节水龙头,让水一滴一滴地流出,在水龙头的正下方放一个盘子,调整盘子的高度,使一水滴刚碰到盘子时,恰好有另一水滴从水龙头开始下落,而空中还有3个正在下落的水滴。测出水龙头到盘子间的距离为。再用秒表测时间,从第一滴水滴离开水龙头开始计时,到第滴水滴落到盘中,共用时间为。
(1)当第一滴水滴落到盘中时,第二滴水滴离开水龙头的距离为 ;
(2)测得的重力加速度为 。
15.(2020春?祁门县校级期中)某自来水管的管口定时滴下水滴,现在管口的正下方放置以金属盘,水滴滴到盘上发出响声,逐渐向上平移金属盘直到看见水滴从管口刚好滴出时,恰好听到水滴滴到盘底的响声,记录盘底的高度,再继续上移盘,第二次,第三次看见水从管口滴出同时听到水滴落到盘底的响声,分别测出盘底离地面的高度和,实验测得,,,.求:
(1)相邻水滴滴出的时间间隔;
(2)自来水管的管口离地面的高度。
16.(2020春?濂溪区校级月考)如图所示,竖直悬挂一根长的直杆,在杆的正下方距离杆下端观察点处有一内径大于杆的直径的圆环。求:
(1)当杆做自由落体运动,直杆全部通过处环所需的时间。
(2)当直杆开始自由下落的瞬间,将环以竖直向上抛出,求直杆全部通过环所需的时间。取,杆和环距离地面足够高,杆的一端进入到另一端离开为通过)
17.(2019秋?常德期末)如图所示,某同学测出一棵苹果树树干部分的高度约为,一个苹果从树冠顶端的树梢上由于受到扰动而自由下落,该同学测出苹果经过树干所用的时间为,重力加速度取,则:
(1)苹果树树冠部分的高度约为多少?
(2)苹果落地时的速度为多大?
18.(2019秋?上月考)一根轻质细线将2个薄铁垫圈、(大小可忽略)连接起来,、间细线长为,距地面一定高度,放手后、自由下落,若、落地时间相差,,求:
(1)距地面的高度;
(2)落地时的速度。
19.(2019春?蓝田县期中)如图所示,悬挂着的一根长为的直杆,在直杆正下方处有一个无底圆筒,若将悬线剪断,直杆通过圆筒所用的时间为,,求:
(1)无底圆筒的长度;
(2)直杆下端穿过圆筒所用的时间是多少?(计算结果保留根号)
答案
1、【分析】苹果做自由落体运动,根据求该苹果下落前距牛顿头部的高度。
【解答】解:根据得:
因当年牛顿躺在树下,那么苹果下落前距牛顿头部的高度为,故正确,错误。
故选:。
2、【分析】本题考查了伽利略斜面实验的物理意义,明确伽利略通过“理想斜面实验”推翻了力是维持运动的原因的错误观点。
【解答】解:亚里士多德认为,力是维持物体运动的原因;伽利略等人认为,力是改变物体运动状态的原因。现在人们普遍认为力是改变物体运动状态的原因的观点是正确的;
而伽利略设计这个理想实验,其目的是为了说明亚里士多德的力是维持物体运动状态的原因的结论是错误的,物体运动不需要力来维持,故错误,正确。
故选:。
3、【分析】小球甲乙分别做自由落体运动,求得甲乙下落的时间,根据同时落体即可求得小球甲的高度。
【解答】解:设小球甲距地面的高度为,下落的时间为,则,解得
小球甲下落所需时间为,则,解得
小球乙下落的时间为,则,解得
联立解得:,故错误,正确;
故选:。
4、【分析】物体做自由落体运动的条件:①只在重力作用下;②从静止开始。只在重力作用下保证了物体的加速度为;从静止开始保证了物体初速度等于零。所以自由落体运动是初速度为0的匀加速直线运动。
【解答】解:、自由落体运动的速度,速度与时间成正比,故正确,错误;
、自由落体运动的加速度为重力加速度,是不变的,故错误;
、位移为,与的图象为过原点的抛物线,故错误。
故选:。
5、【分析】已知小球在连续相等的时间内位移,运用位移差公式和平均速度公式可求出加速度及某点的瞬时速度,再根据速度与位移关系求位移,进而求解。
【解答】解:小球由2到3和1到2的位移差,得;
小球到2点的瞬时速度;
设小球下落点到2点距离,由得,;
小球释放的初始位置与1位置,故正确;
故选:。
6、【分析】根据小球在斜面上的运动情况分析合外力方向关系;根据牛顿第二定律分析在斜面1和斜面2上加速度的大小;根据动能定理确定合外力对小球做的功大小;结合惯性概念分析小球在水平面3上运动的原因。
【解答】解:、小球在右侧斜面1和2向上都做匀减速运动,合外力方向均沿斜面向下,知合外力方向不同,故错误;
、设任一斜面的倾角为,根据牛顿第二定律得,得,所以,小球在斜面1上运动的加速度大于在斜面2上运动的加速度,故错误;
、根据动能定理知,合外力对小球做的功等于小球动能的变化量,而小球动能的变化量相等,所以在斜面1合外力对小球做的功等于在斜面2上合外力对小球做的功,故正确;
、在水平面上小球不受向前的冲力,由于惯性,所以小球在水平面3上运动的更远,故错误。
故选:。
7、【分析】设小球第一次落地时速度为,进而可表示出,,,,根据速度时间关系求解时间之比;
根据速度位移关系求解位移之比;
归纳出小球从开始下落到第次与地面相碰经过时间,根据等比数列前项和公式求解时间;
根据位移的概念求解位移。
【解答】解:、设小球第一次落地时速度为,则有
那么第二次、第三次、第次落地速度分别为,,,
根据速度时间关系可得:
则小球第一次下落的时间与第二次下落的时间之比为:,故正确;
、小球开始下落到第一次与地相碰经过的路程为
小球第一次与地相碰后弹起的高度是:
小球第二次与地相碰后弹起的高度是,则
所以第二次弹起的高度与第一次弹起时高度之比为:,
所以第二次弹起的高度为第一次弹起时高度的,故错误;
、小球第1下落时间为:
小球从第1次与地面相撞到第2次与地面相撞经过的时间为:
小球从第2次与地面相撞到第3次与地面相撞经过的时间为:
小球从第次与地面相撞到第次与地面相撞经过的时间为:
所以小球运动的总时间为:
代入数据解得:,故正确;
、小球最终静止在地面上,所以整个过程中小球运动的总位移为,方向向下,故正确。
故选:。
8、【分析】本题考查了有伽利略“斜面实验”的知识,根据其历史背景我们知道,之所以采用“斜面实验”,注意碍于当时对时间的测量技术、手段落后。
【解答】解:、伽利略时代,没有先进的测量手段和工具,为了“减小”重力作用,采用斜面实验,其实就是为了使物体下落时间长些,便于时间的测量,减小实验误差,故正确,错误;
、根据实验结果,伽利略将实验结论进行合理的外推,得到落体的运动规律,但不能进行直接的计算,故错误;
、伽利略根据实验结果,伽利略将实验结论进行合理的外推,得到落体的运动规律,是科学实验和逻辑推理的完美结合,故正确;
故选:。
9、【分析】根据位移关系可知,要使小球穿过空心管,则小球的位移应比空心管的位移多,根据匀变速直线运动的位移时间公式列式求解小球穿过空心管所用的时间。
若两者无初速度同时释放,则两者都做自由落体运动,小球在空中不能穿过空心管。
【解答】解:、若两者无初速度同时释放,则两者都做自由落体运动,在相同时间内下降的高度相同,可知小球在空中不能穿过空心管,故错误;
、若小球自由下落、管固定不动,小球穿过管的时间是小球到达管的下端与到达管的上端的时间差,根据自由落体运动公式可知:,故错误,正确;
、两者均无初速度释放,但小球提前△时间释放,以管为参考系,小球相对管匀速运动,则有:△,,可知小球穿过管的时间:,故正确。
故选:。
10、【分析】根据加速度大小比较下落快慢,由加速度和自由落体规律求得小球的速度比和落地时间比。
【解答】解:、由为在地球上重力加速度大,故在地球自由下落时和月球上下落时快慢程度不一样,故错误;
、根据自由落体运动规律可知,落地速度可知,落地速度在高度相同的情况下与重力加速度的平方根据成正比,故错误,正确;
、根据自由落体运动规律可知,下落所用时间,下落时间在下落高度相同的情况下与重力加速度的平方根成反比,故正确。
故选:。
11、【分析】两球均做自由落体运动,由速度时间公式求出速度之差与时间的关系式。
【解答】解:两球做自由落体运动,加速度都为重力加速度;以释放第二球开始计时,第一球的速度,经过时间后,第一球的速度,第二球的速度,则两球的速度差为:△。两球的速度之差保持不变。
此后先释放的小球的位移为:
后释放的小球的位移为::
它们之间的距离差为:△
可知它们的间距越来越大
故答案为:越来越大;保持不变
12、【分析】铅球做自由落体运动,由位移公式和速度公式可求解。
【解答】解:铅球做自由落体运动,由位移公式得:
铅球在空中运动时间:
由速度公式得:
故答案为:3,30
13、【分析】自由落体运动是初速度为0的匀加速直线运动,在开始通过连续相等时间内的位移比为,连续相等位移的时间比为,根据求解平均速度。由此分析即可。
【解答】解:根据,内的位移为:
内的位移为:
所以第内的位移为:
根据匀变速直线运动的导出公式可知第内、第内、第内的时间之比为:
根据平均速度公式可得:
故答案为:25,
14、【分析】(1)当一滴水碰到盘子时,恰好有另一滴水从水龙头开始下落,而空中还有3个正在下落的水滴,知水滴将分成时间相等的4份,根据初速度为0的匀加速运动,在相等时间内的位移比为,求出第二滴水离盘子的高度。
(2)从第一滴水离开水龙头开始,到第滴水落至盘中,共用时间为,知道两滴水间的时间间隔,根据求出重力加速度。
【解答】解:(1)由题意可知,水滴将分成时间相等的4份,4份相等时间内位移比为,
总高度为,所以第二滴水滴离水龙头的高度为:,
故第二个水滴离开水龙头的距离为。
(2)从第一滴水离开水龙头开始,到第滴水落至盘中(即滴水离开水龙头),共用时间为,
知道两滴水间的时间间隔为:,
根据得:
解得:
故答案为:,。
15、【分析】(1)水滴做的是自由落体运动,根据△,可以计算时间将的大小;
(2)利用平均速度的关系可以求得第二次时瞬时速度的大小,再计算下降的高度。
【解答】解:(1)设相邻水滴的时间间隔为,由题:
,,
由匀变速直线运动的导出公式:,
解得:
(2)利用公式求得:,
故水管口离第二次小水滴位置的高度:,
因此自来水水管离地面的高度:
答:(1)相邻水滴出的时间间隔为;
(2)自来水水管口离地面的高度为。
16、【分析】(1)杆全部通过点的距离为,根据位移公式可求速度;杆全部通过点需时间为杆的上端到达点的时间减去杆的下端到达点的时间,根据自由落体位移时间公式即可求解;
(2)二者都运动时,分别求出杆与环相遇的时间与分离的时间,然后求出差即可。
【解答】解:(1)根据自由落体位移公式:①
得到下落时间公式:②
杆下端到达点所经过的位移:,代入②式解得③
杆上端到达点所经过的位移:,代入②式解得④
杆通过点所需的时间为:△⑤
(2)将环以竖直向上抛出,杆与环相遇的时间为,则:⑥
杆与环分离的时间为,则:⑦
直杆全部通过环所需的时间:△⑧
联立可得:△⑨
答:(1)当杆做自由落体运动,直杆全部通过处环所需的时间是。
(2)直杆全部通过环所需的时间也是。
17、【分析】设开始下落到达树干的时间为,结合位移关系列式,从而根据位移时间公式求出物体开始下落时树冠的高度,根据求出末速度。
【解答】解:设开始下落到达树干的上沿的时间为,有:
△
代入数据解得:。
则:。
苹果落地的速度为:
答:(1)苹果树树冠部分的高度约为
(2)苹果落地时的速度为。
18、【分析】(1)根据自由落体运动的位移时间公式分别求出两球下落的时间,然后结合两球落地的时间差求出距地面的高度;
(2)结合速度时间公式求出球落地时球的速度。
【解答】解:(1)由匀变速直线运动的位移公式得:①
②
又:△③
④
代入数据解得:,;
(2)球落地的时间与运动的时间相等,此时球的速度为:⑤
代入数据可得:。
答:(1)距地面的高度是;
(2)落地时的速度为。
19、【分析】(1)直杆做的是自由落体运动,根据自由落体运动的规律可以求得下降时杆的速度的大小,再由位移公式可以求得在内杆下降的距离,此距离即为杆和圆筒的总长度的大小;
(2)直杆下端穿过圆筒所用的时间是从杆点落到筒端开始,到杆的端落到端结束,结合位移时间公式进行求解。
【解答】解:取杆的下端点为研究对象,
设下降时点的速度的大小为,根据可得:
直杆通过圆筒的时间是从点进入圆筒开始,到点离开圆筒时结束,
设杆长为,圆筒的长度为,则在内杆下降的距离为,
由位移公式可得:,
解得:,
(2)到时间为,则:
到的时间为,则:
直杆下端穿过圆筒所用时间为:△
联立解得:
答:(1)无底圆筒的长度为;
(2)直杆下端穿过圆筒所用的时间是
声明:试题解析著作权属所有,未经书面同意,不得复制发布
日期:2020/10/13
0:33:47;用户:梦青;邮箱:orFmNt3xQq6ez0-hcFH4Sf27Af1M@weixin.m;学号:38022509
