5.2平行线及其判定 同步练习(含详解)
文档属性
| 名称 | 5.2平行线及其判定 同步练习(含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 327.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 15:16:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
5.2平行线及其判定
学校:___________姓名:___________班级:___________考号:___________
一、单选题
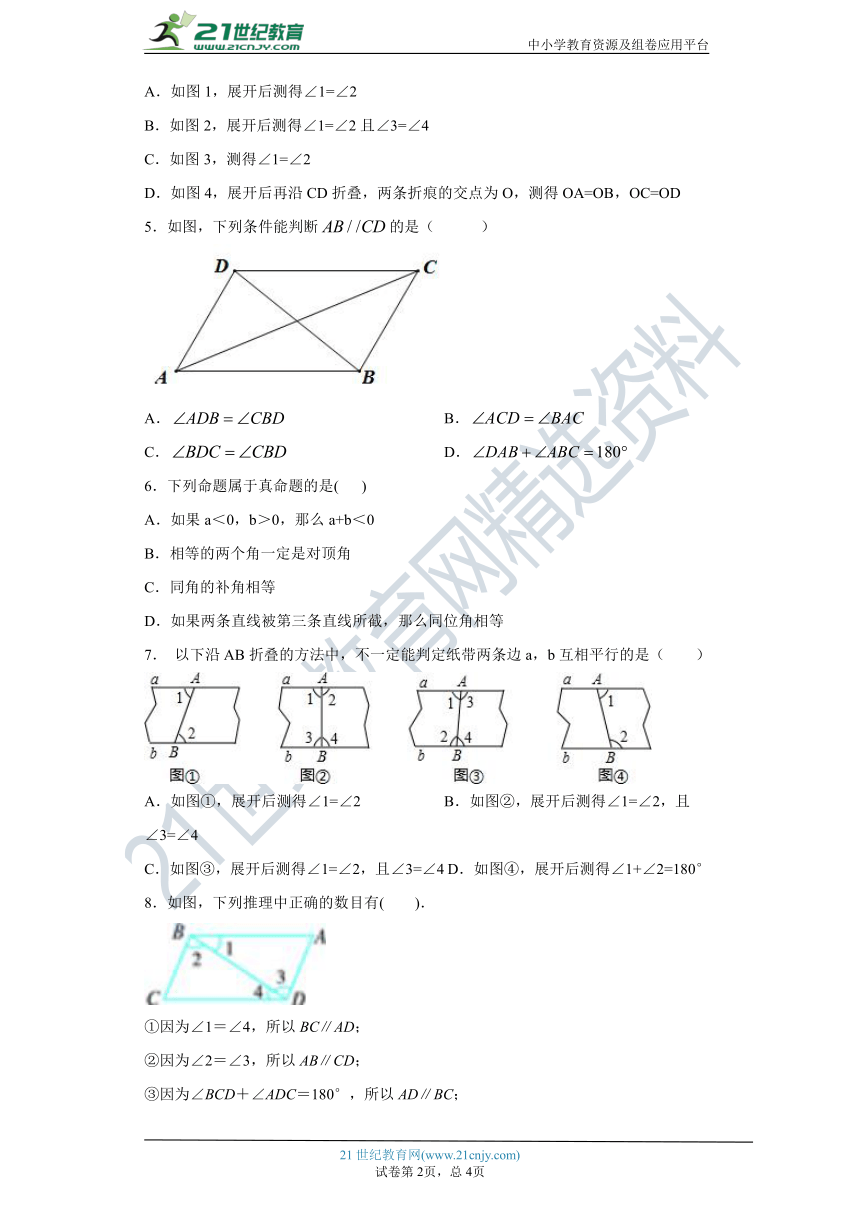
1.如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )
A.∠3=∠4 B.∠D+∠ACD=180°
C.∠D=∠DCE D.∠1=∠2
2.如图,,要使,则的大小是( )
A. B. C. D.
3.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
4.以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2
B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2
D.如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
5.如图,下列条件能判断的是( )
A. B.
C. D.
6.下列命题属于真命题的是( )
A.如果a<0,b>0,那么a+b<0
B.相等的两个角一定是对顶角
C.同角的补角相等
D.如果两条直线被第三条直线所截,那么同位角相等
7. 以下沿AB折叠的方法中,不一定能判定纸带两条边a,b互相平行的是( )
A.如图①,展开后测得∠1=∠2 B.如图②,展开后测得∠1=∠2,且∠3=∠4
C.如图③,展开后测得∠1=∠2,且∠3=∠4 D.如图④,展开后测得∠1+∠2=180°
8.如图,下列推理中正确的数目有( ).
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠C=180°,所以BC∥AD.
A.1个 B.2个
C.3个 D.4个
二、填空题
9.如图,直线a∥b,∠1=55°,则∠2=_____.
10.如图,请写出能判定CE∥AB的一个条件________
11.如图,已知AB∥CD,BC∥DE,那么∠B +∠D =__________.
12.如图,已知直线l与a,b相交,请添加一个条件 ,使a∥b(填一个你认为正确的条件即可)
三、解答题
13.已知AB∥CD,∠1=30°,∠2=50°,∠3=60°,求∠4.
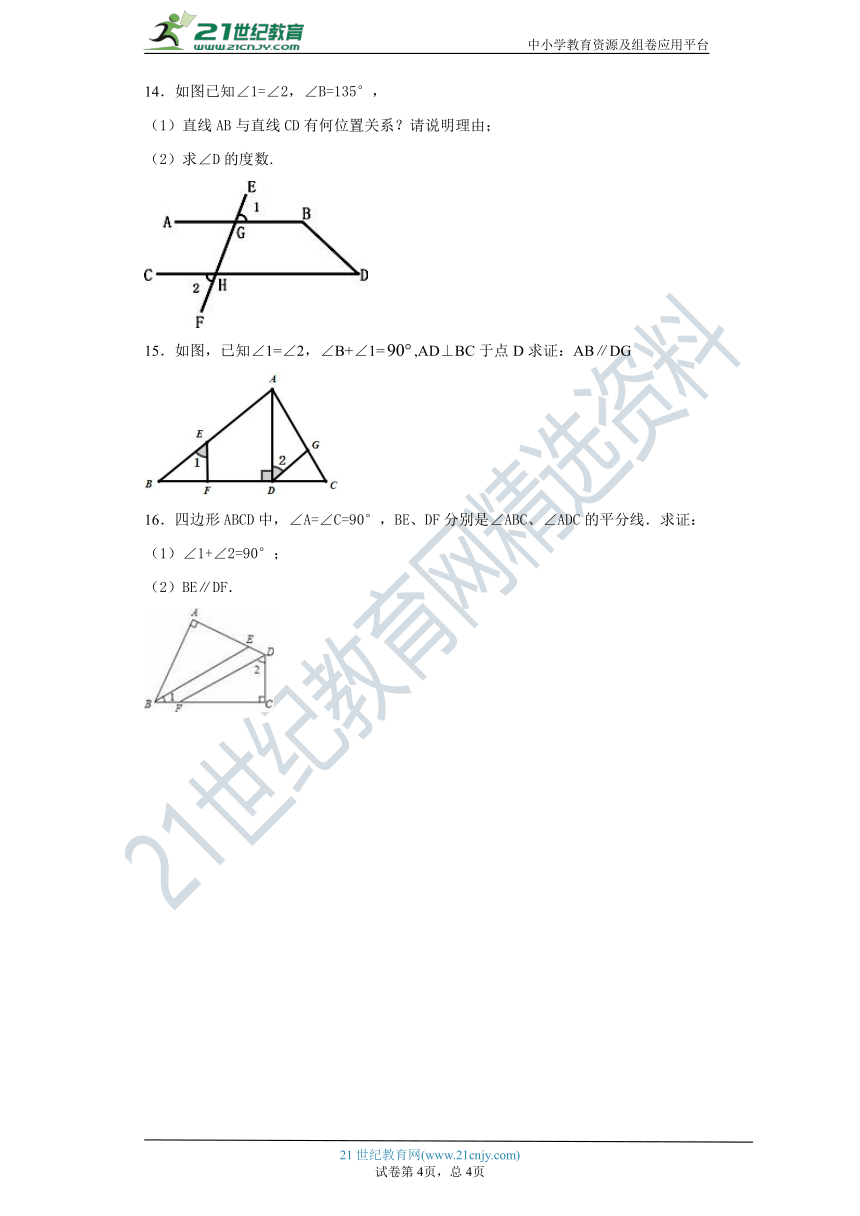
14.如图已知∠1=∠2,∠B=135°,
(1)直线AB与直线CD有何位置关系?请说明理由;
(2)求∠D的度数.
15.如图,已知∠1=∠2,∠B+∠1=,AD⊥BC于点D求证:AB∥DG
16.四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.求证:
(1)∠1+∠2=90°;
(2)BE∥DF.
参考答案
1.D
解析:
详解:
解:A、∵∠3=∠4,∴AC∥BD,故A选项不合题意;
B、∵∠D+∠ACD=180°,∴AC∥BD,故B选项不合题意;
C、∵∠D=∠DCE,∴AC∥BD,故C选项不合题意;
D、∵∠1=∠2,∴AB∥CD,故D选项符合题意.
故选:D.
点睛:
此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.
2.D
解析:
根据同位角相等,两直线平行即可求解.
详解:
解:如果, 那么.
所以要使,则的大小是.
故选D.
点睛:
本题考查的是平行线的判定定理,掌握同位角相等,两直线平行是解题的关键.
3.A
解析:
试题分析:判定两条直线是平行线的方法有:内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补两直线平行等,应结合题意,具体情况,具体分析.
由图形得,有两个相等的同位角,所以只能依据:同位角相等,两直线平行,
故选A.
考点:本题考查的是平行线的判定
点评:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
4.C
解析:
试题分析:A、∠1=∠2,根据内错角相等,两直线平行进行判定,故正确;
B、∵∠1=∠2且∠3=∠4,由图可知∠1+∠2=180°,∠3+∠4=180°,
∴∠1=∠2=∠3=∠4=90°,∴a∥b(内错角相等,两直线平行),故正确;
C、测得∠1=∠2,∵∠1与∠2即不是内错角也不是同位角,∴不一定能判定两直线平行,故错误;
D、在△AOB和△COD中,
,∴△AOB≌△COD,∴∠CAO=∠DBO,
∴a∥b(内错角相等,两直线平行),故正确.故选C.
考点:平行线的判定.
5.B
解析:
根据平行线的判定方法求解.
详解:
解:如果∠ADB=∠CBD,则AD//BC,A错误;
如果∠ACD=∠BAC,则AB//CD,B正确;
如果∠BDC=∠CBD,则CD=CB,而AB//CD不一定成立,C错误;
如果∠DAB+∠ABC=180°,则AD//BC,D错误.
故选B.
点睛:
本题考查平行线的判定,熟练掌握平行线的判定方法是解题关键.
6.C
解析:
综合正负数、绝对值、对顶角、补角、平行线的判定等知识逐个判断4个选项的正误.
详解:
A. 不是真命题,真命题应为“如果a<0,b>0,且|a|>|b|,那么a+b<0”.
B. 不是真命题,真命题应为“两个对顶角相等”.
D. 不是真命题,真命题应为“如果两条平行的直线被第三条直线所截,那么同位角相等”.
故选C.
点睛:
本题考查真假命题的判断,要采用排除法一一判断,其中考查了正负数、绝对值、对顶角、补角、平行线的判定等知识点.
7.C
解析:
根据平行线的判定定理,进行分析,即可解答.
详解:
解:A、∵∠1=∠2,∴a∥b,(内错角相等,两直线平行),
故正确;
B、∵∠1=∠2且∠3=∠4,由图可知∠1+∠2=180°,∠3+∠4=180°,
∴∠1=∠2=∠3=∠4=90°,
∴a∥b(内错角相等,两直线平行),
故正确;
C、测得∠1=∠2,且∠3=∠4
∵∠1与∠2,∠3=∠4,即不是内错角也不是同位角,
∴不一定能判定两直线平行,
故错误;
D、∵∠1+∠2=180°,∴a∥b,(同旁内角互补,两直线平行),
故正确.
故选:C.
点睛:
本题考查了平行线的判定,解决本题的关键是熟记平行线的判定定理.
8.A
解析:
(1)由∠1=∠2不能推导出BC∥AD,所以①中的推理错误;
(2)由∠2=∠3不能推导出AB∥CD,所以②中的推理错误;
(3)由∠BCD+∠ADC=180°能推导出BC∥AD,所以③中推理正确;
(4)由∠BCD+∠ABC=180°不能推导出BC∥AD,所以④中推理错误;
即4个推理中,只有③正确.
故选A.
点睛:在由平行线的判定定理:(1)同位角相等,两直线平行;(2)内错角相等,两直线平行;(3)同旁内角互补,两直线平行;推导得到“两直线平行时”,需注意结论中“平行的直线”是形成条件中的“同位角、内错角和同旁内角”时,被截的两直线.
9.125°.
解析:
先根据平行线的性质求出∠3的度数,再由两角互补的性质求出∠2的度数即可.
详解:
∵直线a∥b,∠1=55°,
∴∠3=∠1=55°,
∵∠2+∠3=180°,
∴∠3=180°﹣∠2=180°﹣55°=125°.
故答案为:125°.
点睛:
本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.熟练的掌握平行线的性质是关键.
10.∠DCE=∠A或∠BCE=∠B或∠ACE+∠A=180?
解析:
根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行添加条件即可.
详解:
∵∠DCE=∠A或∠BCE=∠B或∠ACE+∠A=180?
∴CE∥AB.
故答案为∠DCE=∠A或∠BCE=∠B或∠ACE+∠A=180?.
点睛:
本题考查了平行线的判定,平行线的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考常见题,一般难度不大,需熟练掌握.
11.180°
解析:
试题分析:本题主要利用平行线的性质进行做题.
解:∵AB∥CD,
∴∠B=∠C.
又∵BC∥DE,
∴∠C+∠D=180°,
即∠B+∠D=180度.
故填180.
点评:本题重点考查了平行线的性质,是一道较为简单的题目.
12.∠1=∠3.
解析:
试题分析:根据同位角相等,两直线平行可以判定直线平行.
考点:平行线的判定
13.140°
解析:
试题分析:设直线FE交AB于W,交CD于Q,根据三角形外角性质求出∠AWE,根据平行线的性质求出∠Q,根据三角形外角性质求出∠FCQ,即可求出答案.
解:设直线FE交AB于W,交CD于Q,如图,
∵∠1=30°,∠2=50°,
∴∠AWE=∠2﹣∠1=20°,
∵AB∥CD,
∴∠Q=∠AWE=20°,
∵∠3=60°,
∴∠FCQ=∠3﹣∠Q=40°,
∴∠4=180°﹣∠FCQ=140°.
考点:平行线的性质.
14.(1)见解析;(2)450
解析:
试题分析:根据对顶角相等和同位角相等,两直线平行说明即可;(2)根据两直线平行,同旁内角互补求解即可.
(1)AB∥CD
∵∠2= ∠EHD
又∵∠2= ∠1
∴∠1= ∠EHD
∴AB∥CD
(2)∵AB∥CD
∴∠B+∠D=180?
又∵∠B=135?
∴∠D=180?-135?=45?
15.见解析
解析:
由AD⊥BC可证∠2+∠CDG=90°,根据等角的余角相等可得∠CDG=∠B,从而AB∥DG.
详解:
∵AD⊥BC,
∴∠2+∠CDG=90°,
∵∠1=∠2,∠B+∠1=,
∴∠CDG=∠B,
∴AB∥DG.
点睛:
本题考查了行线的判定方法,熟练掌握平行线的行线的判定方法是解答本题的关键.平行线的判定方法:①两同位角相等,两直线平行;?②内错角相等,两直线平行;③同旁内角互补,两直线平行.也考查了余角的性质.
16.(1)证明见解析;(2)证明见解析.
解析:
试题分析:(1)根据四边形的内角和,可得∠ABC+∠ADC=180°,然后,根据角平分线的性质,即可得出;
(2)由互余可得∠1=∠DFC,根据平行线的判定,即可得出.
试题解析:(1)∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°;
(2)在△FCD中,∵∠C=90°,
∴∠DFC+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE∥DF.
点睛:本题主要考查了平行线的判定和性质,关键是掌握四边形内角和为360°,同位角相等,两直线平行.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
5.2平行线及其判定
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示,点E在AC的延长线上,下列条件中不能判断AC∥BD的是( )
A.∠3=∠4 B.∠D+∠ACD=180°
C.∠D=∠DCE D.∠1=∠2
2.如图,,要使,则的大小是( )
A. B. C. D.
3.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
4.以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2
B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2
D.如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
5.如图,下列条件能判断的是( )
A. B.
C. D.
6.下列命题属于真命题的是( )
A.如果a<0,b>0,那么a+b<0
B.相等的两个角一定是对顶角
C.同角的补角相等
D.如果两条直线被第三条直线所截,那么同位角相等
7. 以下沿AB折叠的方法中,不一定能判定纸带两条边a,b互相平行的是( )
A.如图①,展开后测得∠1=∠2 B.如图②,展开后测得∠1=∠2,且∠3=∠4
C.如图③,展开后测得∠1=∠2,且∠3=∠4 D.如图④,展开后测得∠1+∠2=180°
8.如图,下列推理中正确的数目有( ).
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠C=180°,所以BC∥AD.
A.1个 B.2个
C.3个 D.4个
二、填空题
9.如图,直线a∥b,∠1=55°,则∠2=_____.
10.如图,请写出能判定CE∥AB的一个条件________
11.如图,已知AB∥CD,BC∥DE,那么∠B +∠D =__________.
12.如图,已知直线l与a,b相交,请添加一个条件 ,使a∥b(填一个你认为正确的条件即可)
三、解答题
13.已知AB∥CD,∠1=30°,∠2=50°,∠3=60°,求∠4.
14.如图已知∠1=∠2,∠B=135°,
(1)直线AB与直线CD有何位置关系?请说明理由;
(2)求∠D的度数.
15.如图,已知∠1=∠2,∠B+∠1=,AD⊥BC于点D求证:AB∥DG
16.四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.求证:
(1)∠1+∠2=90°;
(2)BE∥DF.
参考答案
1.D
解析:
详解:
解:A、∵∠3=∠4,∴AC∥BD,故A选项不合题意;
B、∵∠D+∠ACD=180°,∴AC∥BD,故B选项不合题意;
C、∵∠D=∠DCE,∴AC∥BD,故C选项不合题意;
D、∵∠1=∠2,∴AB∥CD,故D选项符合题意.
故选:D.
点睛:
此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.
2.D
解析:
根据同位角相等,两直线平行即可求解.
详解:
解:如果, 那么.
所以要使,则的大小是.
故选D.
点睛:
本题考查的是平行线的判定定理,掌握同位角相等,两直线平行是解题的关键.
3.A
解析:
试题分析:判定两条直线是平行线的方法有:内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补两直线平行等,应结合题意,具体情况,具体分析.
由图形得,有两个相等的同位角,所以只能依据:同位角相等,两直线平行,
故选A.
考点:本题考查的是平行线的判定
点评:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
4.C
解析:
试题分析:A、∠1=∠2,根据内错角相等,两直线平行进行判定,故正确;
B、∵∠1=∠2且∠3=∠4,由图可知∠1+∠2=180°,∠3+∠4=180°,
∴∠1=∠2=∠3=∠4=90°,∴a∥b(内错角相等,两直线平行),故正确;
C、测得∠1=∠2,∵∠1与∠2即不是内错角也不是同位角,∴不一定能判定两直线平行,故错误;
D、在△AOB和△COD中,
,∴△AOB≌△COD,∴∠CAO=∠DBO,
∴a∥b(内错角相等,两直线平行),故正确.故选C.
考点:平行线的判定.
5.B
解析:
根据平行线的判定方法求解.
详解:
解:如果∠ADB=∠CBD,则AD//BC,A错误;
如果∠ACD=∠BAC,则AB//CD,B正确;
如果∠BDC=∠CBD,则CD=CB,而AB//CD不一定成立,C错误;
如果∠DAB+∠ABC=180°,则AD//BC,D错误.
故选B.
点睛:
本题考查平行线的判定,熟练掌握平行线的判定方法是解题关键.
6.C
解析:
综合正负数、绝对值、对顶角、补角、平行线的判定等知识逐个判断4个选项的正误.
详解:
A. 不是真命题,真命题应为“如果a<0,b>0,且|a|>|b|,那么a+b<0”.
B. 不是真命题,真命题应为“两个对顶角相等”.
D. 不是真命题,真命题应为“如果两条平行的直线被第三条直线所截,那么同位角相等”.
故选C.
点睛:
本题考查真假命题的判断,要采用排除法一一判断,其中考查了正负数、绝对值、对顶角、补角、平行线的判定等知识点.
7.C
解析:
根据平行线的判定定理,进行分析,即可解答.
详解:
解:A、∵∠1=∠2,∴a∥b,(内错角相等,两直线平行),
故正确;
B、∵∠1=∠2且∠3=∠4,由图可知∠1+∠2=180°,∠3+∠4=180°,
∴∠1=∠2=∠3=∠4=90°,
∴a∥b(内错角相等,两直线平行),
故正确;
C、测得∠1=∠2,且∠3=∠4
∵∠1与∠2,∠3=∠4,即不是内错角也不是同位角,
∴不一定能判定两直线平行,
故错误;
D、∵∠1+∠2=180°,∴a∥b,(同旁内角互补,两直线平行),
故正确.
故选:C.
点睛:
本题考查了平行线的判定,解决本题的关键是熟记平行线的判定定理.
8.A
解析:
(1)由∠1=∠2不能推导出BC∥AD,所以①中的推理错误;
(2)由∠2=∠3不能推导出AB∥CD,所以②中的推理错误;
(3)由∠BCD+∠ADC=180°能推导出BC∥AD,所以③中推理正确;
(4)由∠BCD+∠ABC=180°不能推导出BC∥AD,所以④中推理错误;
即4个推理中,只有③正确.
故选A.
点睛:在由平行线的判定定理:(1)同位角相等,两直线平行;(2)内错角相等,两直线平行;(3)同旁内角互补,两直线平行;推导得到“两直线平行时”,需注意结论中“平行的直线”是形成条件中的“同位角、内错角和同旁内角”时,被截的两直线.
9.125°.
解析:
先根据平行线的性质求出∠3的度数,再由两角互补的性质求出∠2的度数即可.
详解:
∵直线a∥b,∠1=55°,
∴∠3=∠1=55°,
∵∠2+∠3=180°,
∴∠3=180°﹣∠2=180°﹣55°=125°.
故答案为:125°.
点睛:
本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.熟练的掌握平行线的性质是关键.
10.∠DCE=∠A或∠BCE=∠B或∠ACE+∠A=180?
解析:
根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行添加条件即可.
详解:
∵∠DCE=∠A或∠BCE=∠B或∠ACE+∠A=180?
∴CE∥AB.
故答案为∠DCE=∠A或∠BCE=∠B或∠ACE+∠A=180?.
点睛:
本题考查了平行线的判定,平行线的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考常见题,一般难度不大,需熟练掌握.
11.180°
解析:
试题分析:本题主要利用平行线的性质进行做题.
解:∵AB∥CD,
∴∠B=∠C.
又∵BC∥DE,
∴∠C+∠D=180°,
即∠B+∠D=180度.
故填180.
点评:本题重点考查了平行线的性质,是一道较为简单的题目.
12.∠1=∠3.
解析:
试题分析:根据同位角相等,两直线平行可以判定直线平行.
考点:平行线的判定
13.140°
解析:
试题分析:设直线FE交AB于W,交CD于Q,根据三角形外角性质求出∠AWE,根据平行线的性质求出∠Q,根据三角形外角性质求出∠FCQ,即可求出答案.
解:设直线FE交AB于W,交CD于Q,如图,
∵∠1=30°,∠2=50°,
∴∠AWE=∠2﹣∠1=20°,
∵AB∥CD,
∴∠Q=∠AWE=20°,
∵∠3=60°,
∴∠FCQ=∠3﹣∠Q=40°,
∴∠4=180°﹣∠FCQ=140°.
考点:平行线的性质.
14.(1)见解析;(2)450
解析:
试题分析:根据对顶角相等和同位角相等,两直线平行说明即可;(2)根据两直线平行,同旁内角互补求解即可.
(1)AB∥CD
∵∠2= ∠EHD
又∵∠2= ∠1
∴∠1= ∠EHD
∴AB∥CD
(2)∵AB∥CD
∴∠B+∠D=180?
又∵∠B=135?
∴∠D=180?-135?=45?
15.见解析
解析:
由AD⊥BC可证∠2+∠CDG=90°,根据等角的余角相等可得∠CDG=∠B,从而AB∥DG.
详解:
∵AD⊥BC,
∴∠2+∠CDG=90°,
∵∠1=∠2,∠B+∠1=,
∴∠CDG=∠B,
∴AB∥DG.
点睛:
本题考查了行线的判定方法,熟练掌握平行线的行线的判定方法是解答本题的关键.平行线的判定方法:①两同位角相等,两直线平行;?②内错角相等,两直线平行;③同旁内角互补,两直线平行.也考查了余角的性质.
16.(1)证明见解析;(2)证明见解析.
解析:
试题分析:(1)根据四边形的内角和,可得∠ABC+∠ADC=180°,然后,根据角平分线的性质,即可得出;
(2)由互余可得∠1=∠DFC,根据平行线的判定,即可得出.
试题解析:(1)∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∴2(∠1+∠2)=180°,
∴∠1+∠2=90°;
(2)在△FCD中,∵∠C=90°,
∴∠DFC+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE∥DF.
点睛:本题主要考查了平行线的判定和性质,关键是掌握四边形内角和为360°,同位角相等,两直线平行.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
