5.1.2垂线 同步练习(含详解)
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
5.1.2垂线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
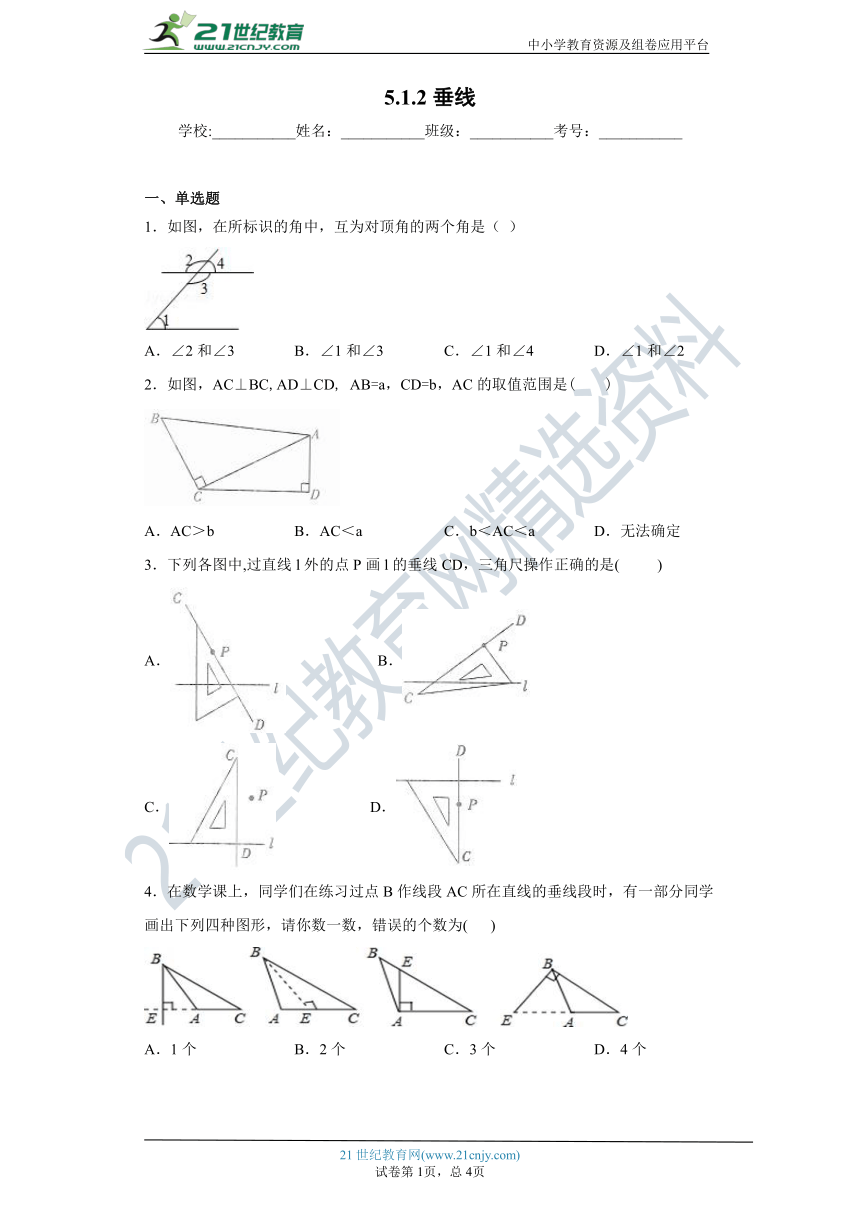
1.如图,在所标识的角中,互为对顶角的两个角是( )
A.∠2和∠3 B.∠1和∠3 C.∠1和∠4 D.∠1和∠2
2.如图,AC⊥BC,AD⊥CD, AB=a,CD=b,AC的取值范围是( )
A.AC>b B.AC<a C.b<AC<a D.无法确定
3.下列各图中,过直线l外的点P画l的垂线CD,三角尺操作正确的是( )
A. B. C. D.
4.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,请你数一数,错误的个数为( )
A.1个 B.2个 C.3个 D.4个
5.通过观察你能肯定的是( )
A.图形中线段是否相等 B.图形中线段是否平行
C.图形中线段是否相交 D.图形中线段是否垂直
6.下列图形中,线段PQ的长度表示点P到直线L的距离的是( )
A. B. C. D.
7.如图,三角形中,,于点,则下列说法错误的是
A.点到直线的距离为线段的长度
B.点到直线的距离为线段的长度
C.点到直线的距离为线段的长度
D.点到直线的距离为线段的长度
8.已知直角三角形ABC中,∠ACB=90°,AC=4,BC=3,AB=5,点D从点A到点B沿AB运动,CD=x,则x的取值范围是( ) .
A. ≤x≤3 B. ≤x<4 C. ≤x≤4 D. ≤x≤5
二、填空题
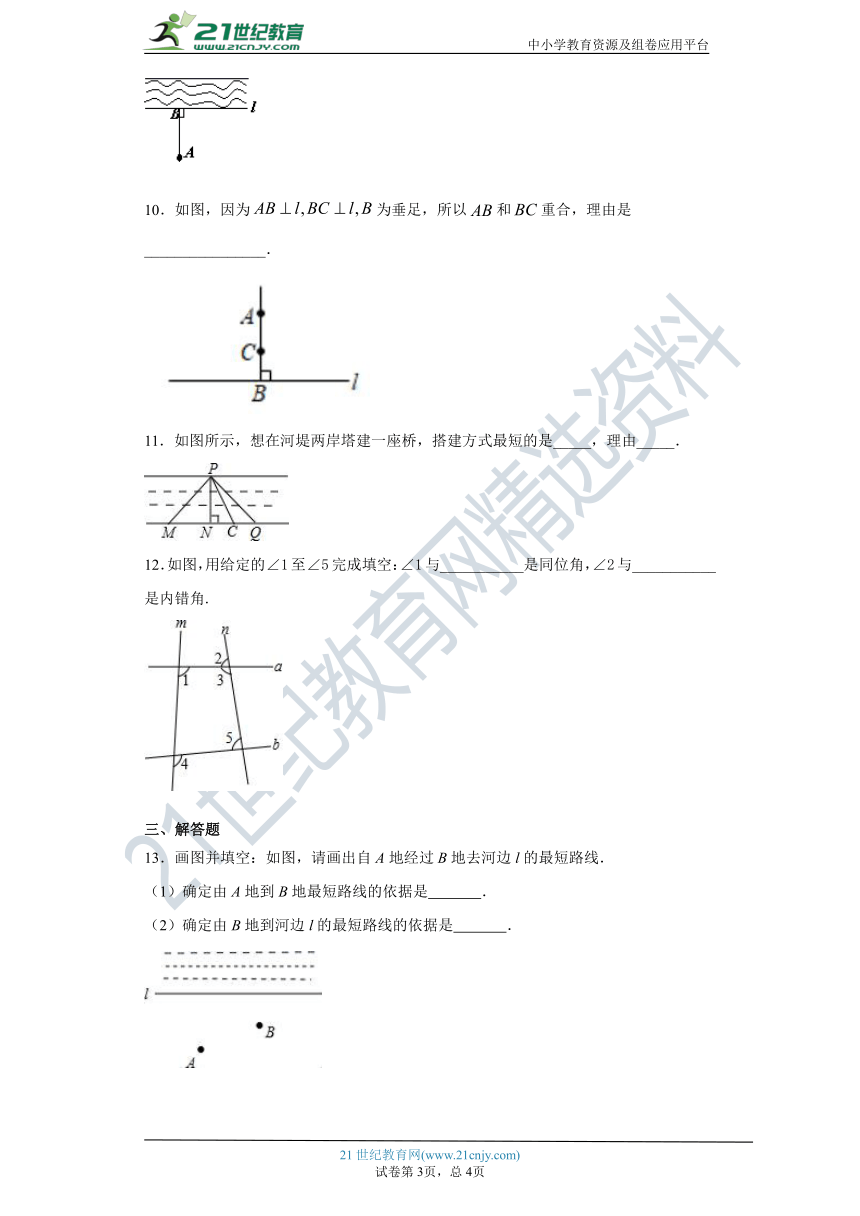
9.如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短.
理由是_______________________.
10.如图,因为为垂足,所以和重合,理由是________________.
11.如图所示,想在河堤两岸塔建一座桥,搭建方式最短的是_____,理由_____.
12.如图,用给定的∠1至∠5完成填空:∠1与___________是同位角,∠2与___________是内错角.
三、解答题
13.画图并填空:如图,请画出自A地经过B地去河边l的最短路线.
(1)确定由A地到B地最短路线的依据是 .
(2)确定由B地到河边l的最短路线的依据是 .
14.如图,直线AB、CD相交于点O,OE⊥AB,且∠DOE=4∠COE,求∠AOD的度数.
15.如图,已知点E在直线AB外,请用三角板与直尺画图,并回答第(3)题:
(1)过E作直线CD,使CD∥AB;
(2)过E作直线EF,使EF⊥AB,垂足为F;
(3)请判断直线CD与EF的位置关系,并说明理由.
16.如图,BE是AB的延长线,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?
(1)∠A和∠D;
(2)∠A和∠CBA;
(3)∠C和∠CBE.
参考答案
1.A
解析:
试题分析:两条直线相交后,所得的只有一个公共顶点,且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角.
解:根据同位角、同旁内角、邻补角、对顶角的定义进行判断,
A、∠2和∠3是对顶角,正确;
B、∠1和∠3是同旁内角,错误;
C、∠1和∠4是同位角,错误;
D、∠1和∠2的邻补角是内错角,错误.
故选A.
【点评】解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.
2.C
解析:
根据垂线段最短即可得到AC的取值范围.
详解:
∵AC⊥BC,AD⊥CD,AB=a,CD=b,
∴CD<AC<AB,
即b<AC<a.
故选C.
点睛:
本题考查了垂线段最短的性质,准确识图是解题的关键.
3.D
解析:
解:根据垂线的作法,用直角三角板的一条直角边与l重合,另一条直角边过点P后沿直角边画直线,可得D的画法正确.故选D.
4.D
解析:
试题解析:从左向右第一个图形中,BE不是线段,故错误;
第二个图形中,BE不垂直AC,所以错误;
第三个图形中,是过点E作的AC的垂线,所以错误;
第四个图形中,过点C作的BE的垂线,也错误.
故选D.
5.C
解析:试题解析:图形中的线段能否相等、平行、垂直往往目测不准,但是能判断两条直线是否相交,当有一个交点时即可相交,
故选C.
6.C
解析:
根据点到直线的距离概念,逐一判断选项,即可得到答案.
详解:
A. PQ不垂直于直线l,故不符合题意,
B. PQ不垂直于直线l,故不符合题意,
C. PQ⊥l,即:线段PQ的长度表示点P到直线l的距离,故符合题意,
D. PQ不垂直于直线l,故不符合题意,
故选C.
点睛:
本题主要考查点到直线的距离概念,掌握“点与直线之间的垂线段的长度,叫做点到直线的距离”是解题的关键.
7.A
解析:
根据点到直线的距离为点到直线的垂线段的长度来分析即可.
详解:
解:∵∠ACB=90°,
∴AC⊥BC
根据点到直线的距离为点到直线的垂线段的长度来分析:
A:点A到直线BC的距离为线段AC的长度,而不是线段AB的长度,故A错误.
故选:A.
点睛:
本题考查了点到直线的距离的基本概念,属于基础题型,难度不大.
8.C
解析:
分析:点D在A点时,x值最大,当点D运动到CD⊥AB时,x值最小,求出x的值即可.
详解:点D在A点时,x值最大,此时x=4,
当点D运动到CD⊥AB时,x值最小,
根据直角三角形的面积公式,得AC?BC=AB?CD,
则CD==,
故 ≤x≤4,
故选:C.
点睛:此题考查了点到直线的距离和直角三角形的性质,根据直角三角形的面积等于两条直角边的乘积的一半,也等于斜边与斜边上的高的积的一半,进行计算.
9.垂线段最短
解析:
试题分析:点到直线的所有线段中垂线段最短.
考点:垂线段的性质
10.在同一平面内,过一点有且只有一条直线与已知直线垂直
解析:
根据垂线的性质解答即可.
详解:
解:如图,因为为垂足,所以和重合,理由是:在同一平面内,过一点有且只有一条直线与已知直线垂直.
故答案为:在同一平面内,过一点有且只有一条直线与已知直线垂直.
点睛:
此题考查了垂线的性质,正确把握垂线的性质是解题的关键.
11.PN, 垂线段最短
解析:
详解:
∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为PM,垂线段最短.
12.∠4 ∠1
解析:
根据同位角的定义可知∠1与∠4是同位角,
根据内错角的定义可知∠2与∠1是内错角,
故答案为:∠4,∠1.
13.(1)图详见解析,两点之间,线段最短;(2)图详见解析,垂线段最短.
解析:
(1)根据两点之间,线段最短,连接AB,线段AB即为由A地到B地最短路线;
(2)根据垂线段最短,过点B作BD⊥l,垂足为点D,线段BD即为由B地到河边l的最短路线.
详解:
解:连接AB,过点B作BD⊥l,垂足为点D,自A地经过B地去河边l的最短路线,如图所示.
(1)确定由A地到B地最短路线的依据是两点之间,线段最短.
(2)确定由B地到河边l的最短路线的依据是垂线段最短.
点睛:
此题考查的是路径的最值问题,掌握两点之间,线段最短和垂线段最短是解决此题的关键.
14.126º
解析:
试题分析:由∠DOE=4∠COE结合平角的定义可求得∠COE的度数,再结合垂直的定义求解即可.
∵∠DOE=4∠COE,∠DOE+∠COE=180°
∴∠COE=36°
∵OE⊥AB
∴∠BOE=90°
∴∠COB=126°
∴∠AOD=∠COB=126°.
考点:平角的定义,垂直的定义,角的比较大小,对顶角相等
点评:本题属于基础应用题,只需学生熟练掌握角的大小关系,即可完成.
15.(1)、(2)如图所示:
(3)CD⊥EF.理由见解析
解析:
试题分析:(1)根据平行线的作法用直尺和三角板作图即可;(2)利用三角板的两条直角边作图即可;(3)根据平行线的性质和垂直的定义说明.
解:(1)如图;
(2)如图;
(3)CD⊥EF.
∵EF⊥AB ,
∴∠EFB=90?,
∵CD∥AB,
∴∠DEF+ ∠EFB=180?,
∴∠DEF=180?-90?=90?,
∴CD⊥EF.
16.见解析
解析:
试题分析:(1)(2)同旁内角,“同旁”指在第三条直线的同侧;“内”指在被截两条直线之间.
(3)内错角,“内”指在被截两条直线之间;“错”即交错,在第三条直线的两侧.(一个角在第三直线左侧,另一角在第三直线右侧)
试题解析:(1)∠A和∠D是由直线AE、CD被直线AD所截形成的,它们是同旁内角;
(2)∠A和∠CBA是由直线AD、BC被直线AE所截形成的,它们是同旁内角;
(3)∠C和∠CBE是由直线CD、AE被直线BC所截形成的,它们是内错角.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
5.1.2垂线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在所标识的角中,互为对顶角的两个角是( )
A.∠2和∠3 B.∠1和∠3 C.∠1和∠4 D.∠1和∠2
2.如图,AC⊥BC,AD⊥CD, AB=a,CD=b,AC的取值范围是( )
A.AC>b B.AC<a C.b<AC<a D.无法确定
3.下列各图中,过直线l外的点P画l的垂线CD,三角尺操作正确的是( )
A. B. C. D.
4.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,请你数一数,错误的个数为( )
A.1个 B.2个 C.3个 D.4个
5.通过观察你能肯定的是( )
A.图形中线段是否相等 B.图形中线段是否平行
C.图形中线段是否相交 D.图形中线段是否垂直
6.下列图形中,线段PQ的长度表示点P到直线L的距离的是( )
A. B. C. D.
7.如图,三角形中,,于点,则下列说法错误的是
A.点到直线的距离为线段的长度
B.点到直线的距离为线段的长度
C.点到直线的距离为线段的长度
D.点到直线的距离为线段的长度
8.已知直角三角形ABC中,∠ACB=90°,AC=4,BC=3,AB=5,点D从点A到点B沿AB运动,CD=x,则x的取值范围是( ) .
A. ≤x≤3 B. ≤x<4 C. ≤x≤4 D. ≤x≤5
二、填空题
9.如图,把小河里的水引到田地A处就作AB⊥l,垂足为B,沿AB挖水沟,水沟最短.
理由是_______________________.
10.如图,因为为垂足,所以和重合,理由是________________.
11.如图所示,想在河堤两岸塔建一座桥,搭建方式最短的是_____,理由_____.
12.如图,用给定的∠1至∠5完成填空:∠1与___________是同位角,∠2与___________是内错角.
三、解答题
13.画图并填空:如图,请画出自A地经过B地去河边l的最短路线.
(1)确定由A地到B地最短路线的依据是 .
(2)确定由B地到河边l的最短路线的依据是 .
14.如图,直线AB、CD相交于点O,OE⊥AB,且∠DOE=4∠COE,求∠AOD的度数.
15.如图,已知点E在直线AB外,请用三角板与直尺画图,并回答第(3)题:
(1)过E作直线CD,使CD∥AB;
(2)过E作直线EF,使EF⊥AB,垂足为F;
(3)请判断直线CD与EF的位置关系,并说明理由.
16.如图,BE是AB的延长线,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?
(1)∠A和∠D;
(2)∠A和∠CBA;
(3)∠C和∠CBE.
参考答案
1.A
解析:
试题分析:两条直线相交后,所得的只有一个公共顶点,且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角.
解:根据同位角、同旁内角、邻补角、对顶角的定义进行判断,
A、∠2和∠3是对顶角,正确;
B、∠1和∠3是同旁内角,错误;
C、∠1和∠4是同位角,错误;
D、∠1和∠2的邻补角是内错角,错误.
故选A.
【点评】解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.
2.C
解析:
根据垂线段最短即可得到AC的取值范围.
详解:
∵AC⊥BC,AD⊥CD,AB=a,CD=b,
∴CD<AC<AB,
即b<AC<a.
故选C.
点睛:
本题考查了垂线段最短的性质,准确识图是解题的关键.
3.D
解析:
解:根据垂线的作法,用直角三角板的一条直角边与l重合,另一条直角边过点P后沿直角边画直线,可得D的画法正确.故选D.
4.D
解析:
试题解析:从左向右第一个图形中,BE不是线段,故错误;
第二个图形中,BE不垂直AC,所以错误;
第三个图形中,是过点E作的AC的垂线,所以错误;
第四个图形中,过点C作的BE的垂线,也错误.
故选D.
5.C
解析:试题解析:图形中的线段能否相等、平行、垂直往往目测不准,但是能判断两条直线是否相交,当有一个交点时即可相交,
故选C.
6.C
解析:
根据点到直线的距离概念,逐一判断选项,即可得到答案.
详解:
A. PQ不垂直于直线l,故不符合题意,
B. PQ不垂直于直线l,故不符合题意,
C. PQ⊥l,即:线段PQ的长度表示点P到直线l的距离,故符合题意,
D. PQ不垂直于直线l,故不符合题意,
故选C.
点睛:
本题主要考查点到直线的距离概念,掌握“点与直线之间的垂线段的长度,叫做点到直线的距离”是解题的关键.
7.A
解析:
根据点到直线的距离为点到直线的垂线段的长度来分析即可.
详解:
解:∵∠ACB=90°,
∴AC⊥BC
根据点到直线的距离为点到直线的垂线段的长度来分析:
A:点A到直线BC的距离为线段AC的长度,而不是线段AB的长度,故A错误.
故选:A.
点睛:
本题考查了点到直线的距离的基本概念,属于基础题型,难度不大.
8.C
解析:
分析:点D在A点时,x值最大,当点D运动到CD⊥AB时,x值最小,求出x的值即可.
详解:点D在A点时,x值最大,此时x=4,
当点D运动到CD⊥AB时,x值最小,
根据直角三角形的面积公式,得AC?BC=AB?CD,
则CD==,
故 ≤x≤4,
故选:C.
点睛:此题考查了点到直线的距离和直角三角形的性质,根据直角三角形的面积等于两条直角边的乘积的一半,也等于斜边与斜边上的高的积的一半,进行计算.
9.垂线段最短
解析:
试题分析:点到直线的所有线段中垂线段最短.
考点:垂线段的性质
10.在同一平面内,过一点有且只有一条直线与已知直线垂直
解析:
根据垂线的性质解答即可.
详解:
解:如图,因为为垂足,所以和重合,理由是:在同一平面内,过一点有且只有一条直线与已知直线垂直.
故答案为:在同一平面内,过一点有且只有一条直线与已知直线垂直.
点睛:
此题考查了垂线的性质,正确把握垂线的性质是解题的关键.
11.PN, 垂线段最短
解析:
详解:
∵PM⊥MN,
∴由垂线段最短可知PM是最短的,
故答案为PM,垂线段最短.
12.∠4 ∠1
解析:
根据同位角的定义可知∠1与∠4是同位角,
根据内错角的定义可知∠2与∠1是内错角,
故答案为:∠4,∠1.
13.(1)图详见解析,两点之间,线段最短;(2)图详见解析,垂线段最短.
解析:
(1)根据两点之间,线段最短,连接AB,线段AB即为由A地到B地最短路线;
(2)根据垂线段最短,过点B作BD⊥l,垂足为点D,线段BD即为由B地到河边l的最短路线.
详解:
解:连接AB,过点B作BD⊥l,垂足为点D,自A地经过B地去河边l的最短路线,如图所示.
(1)确定由A地到B地最短路线的依据是两点之间,线段最短.
(2)确定由B地到河边l的最短路线的依据是垂线段最短.
点睛:
此题考查的是路径的最值问题,掌握两点之间,线段最短和垂线段最短是解决此题的关键.
14.126º
解析:
试题分析:由∠DOE=4∠COE结合平角的定义可求得∠COE的度数,再结合垂直的定义求解即可.
∵∠DOE=4∠COE,∠DOE+∠COE=180°
∴∠COE=36°
∵OE⊥AB
∴∠BOE=90°
∴∠COB=126°
∴∠AOD=∠COB=126°.
考点:平角的定义,垂直的定义,角的比较大小,对顶角相等
点评:本题属于基础应用题,只需学生熟练掌握角的大小关系,即可完成.
15.(1)、(2)如图所示:
(3)CD⊥EF.理由见解析
解析:
试题分析:(1)根据平行线的作法用直尺和三角板作图即可;(2)利用三角板的两条直角边作图即可;(3)根据平行线的性质和垂直的定义说明.
解:(1)如图;
(2)如图;
(3)CD⊥EF.
∵EF⊥AB ,
∴∠EFB=90?,
∵CD∥AB,
∴∠DEF+ ∠EFB=180?,
∴∠DEF=180?-90?=90?,
∴CD⊥EF.
16.见解析
解析:
试题分析:(1)(2)同旁内角,“同旁”指在第三条直线的同侧;“内”指在被截两条直线之间.
(3)内错角,“内”指在被截两条直线之间;“错”即交错,在第三条直线的两侧.(一个角在第三直线左侧,另一角在第三直线右侧)
试题解析:(1)∠A和∠D是由直线AE、CD被直线AD所截形成的,它们是同旁内角;
(2)∠A和∠CBA是由直线AD、BC被直线AE所截形成的,它们是同旁内角;
(3)∠C和∠CBE是由直线CD、AE被直线BC所截形成的,它们是内错角.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
