5.3.1平行线的性质 同步练习(含详解)
文档属性
| 名称 | 5.3.1平行线的性质 同步练习(含详解) |
|
|
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
5.3.1平行线的性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下面四个图形中,与是邻补角的是( )
A. B. C. D.
2.如图,AB // CD,AD=CD,∠1=70°,则∠2的度数是( )
A.40° B.50° C.55° D.60°
3.下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行
B.两直线被第三条直线所截,同旁内角互补
C.不相交的两条直线叫平行线
D.邻补角的平分线互相垂直
4.如图,Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,若∠BCE=35°,则∠A的度数为( )
A. B. C. D.
5.如图,将一张含有角的三角形纸片的两个顶点放在直尺的两条对边上,若,则的度数是( )
A. B. C. D.
6.如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2的度数是( )
A.55° B.65° C.75° D.85°
7.如图,AB∥CD,DE⊥CE,∠1=36°,则∠DCE的度数为( )
A.36° B.44° C.66° D.54°
8.如图,AB∥DC,ED∥BC,AE∥BD,那么图中与△ABD面积相等的三角形有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,直线,直线与直线,都相交.若,则_______.
10.如右图,已知直线、被直线所截,∠1=60°, 则当∠2= °时,∥.
11.如图,把一个直角三角尺的直角顶点放在直尺的一边上,若∠1=52°,则∠2= _______°.
12. 如图,已知直线,点C,D在直线a上,点在直线b上,线段相交于点E,若的面积为,,,则的面积为?_______________________?.
13.如图,已知AB∥CD,∠EAF =∠EAB,∠ECF=∠ECD ,∠AFC=62°,则∠AEC度数是________
三、解答题
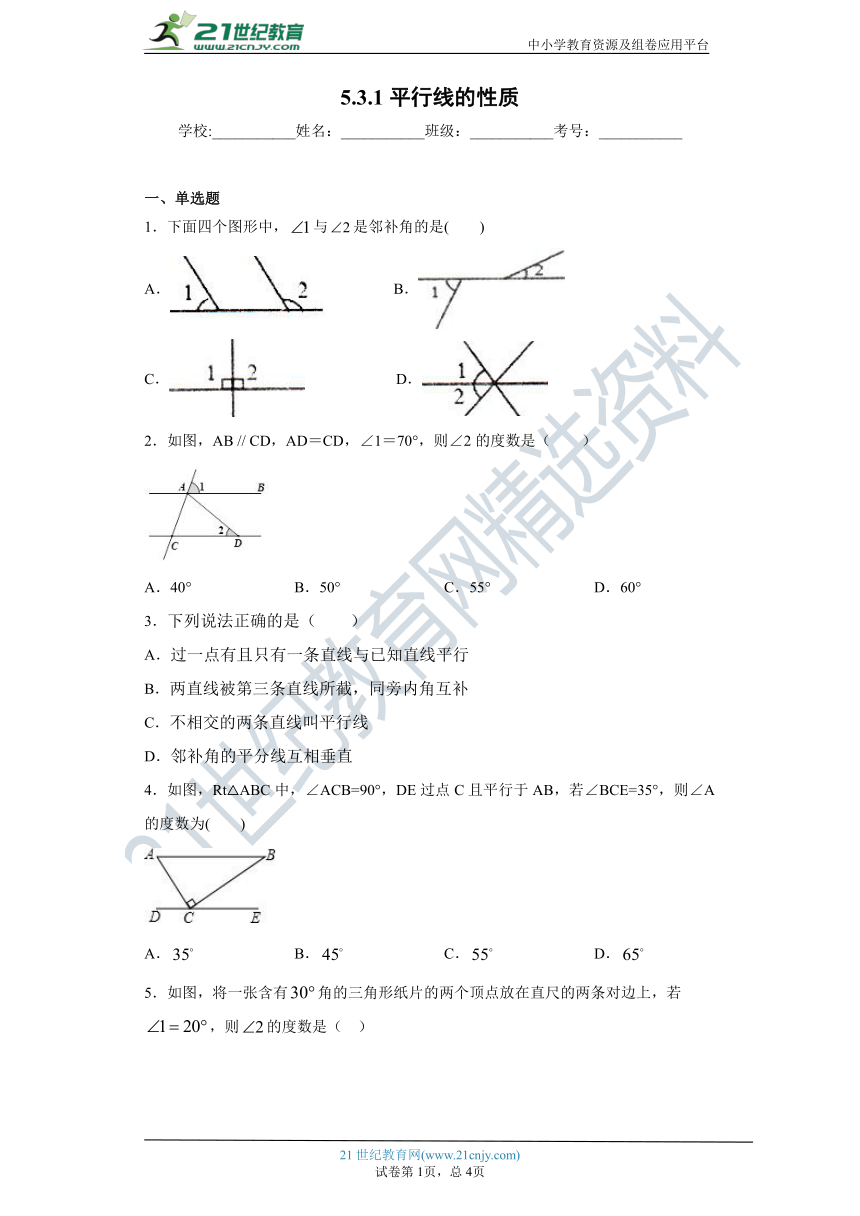
14.如图,,,试说明:.
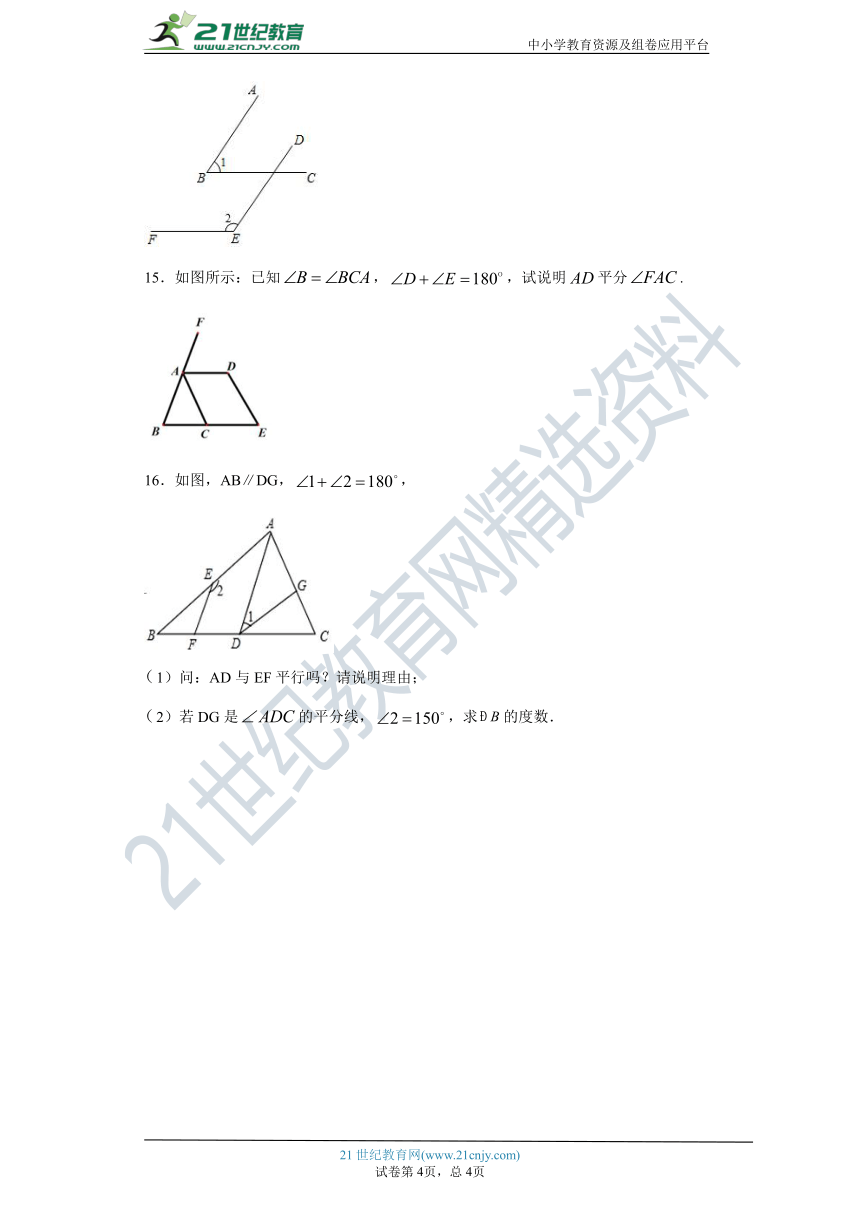
15.如图所示:已知,,试说明平分.
16.如图,AB∥DG,,
1)问:AD与EF平行吗?请说明理由;
2)若DG是的平分线,,求的度数.
参考答案
1.C
解析:
根据邻补角的定义,相邻且互补的两个角互为邻补角进行判断.
详解:
解:A、B选项,∠1与∠2没有公共顶点且不相邻,不是邻补角;
C选项互补且相邻,是邻补角;
D选项∠1与∠2不互补,不是邻补角;
故选C.
点睛:
本题考查邻补角的定义,是一个需要熟记的内容.
2.A
解析:
先根据平行线的性质求出∠ACD的度数,再由AC=CD得出∠CAD的度数,根据三角形内角和定理即可得出结论.
详解:
解:∵AB∥CD,∠1=70°,
∴∠ACD=∠1=70°.
∵AD=CD,
∴∠CAD=∠ACD=70°,
∴∠2=180°-∠ACD-∠CAD=180°-70°-70°=40°.
故选:A.
点睛:
本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.
3.D
解析:A选项正确说法应该是:过直线外一点有且只有一条直线与已知直线平行,故是错误的;
B选项正确说法应该是:两条平行线被第三条直线所截,同旁内角互补,故是错误的;
C选项正确说法应该是:在同一平面内,不相交的两条直线叫平行线,故是错误的;
D选项是正解的;
故选D。
4.C
解析:
分析:题中有三个条件,图形为常见图形,可先由AB∥DE,∠BCE=35°,根据两直线平行,内错角相等求出∠B,然后根据三角形内角和为180°求出∠A.
详解:∵AB∥DE,∠BCE=35°,∴∠B=∠BCE=35°(两直线平行,内错角相等).
又∵∠ACB=90°,∴∠A=90°﹣35°=55°(在直角三角形中,两个锐角互余).
故选C.
点睛:看到两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.
5.C
解析:
利用平行线的性质,三角形的外角的性质解决问题即可;
详解:
解:如图,
∵AB∥CD,
∴∠3=∠2,
∴∠3=∠1+30°,
∵∠1=20°,
∴∠3=∠2=50°;
故选:C.
点睛:
本题主要考查平行线的性质,三角形的外角等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
6.B
解析:
根据两直线平行,同旁内角互补可求出∠AFD的度数,然后根据对顶角相等求出∠2的度数.
详解:
∵AB∥CD,
∴∠1+∠AFD=180°,
∵∠1=115°,
∴∠AFD=65°,
∵∠2和∠AFD是对顶角,
∴∠2=∠AFD=65°,
故选B.
点睛:
本题主要考查了平行线的性质,解题的关键是掌握两直线平行,同旁内角互补.
7.D
解析:
∵DE⊥CE,
∴∠CED=90?,
∴∠BEC=180 ?-90 ?-36 ?=54 ?.
∵AB∥CD,
∴∠DCE=∠BEC=54 ?.
故选D.
8.C
解析:
根据等高模型,同底等高的三角形的面积相等即可判断;
详解:
解:∵AE∥BD,
∴S△ABD=S△BDE,
∵DE∥BC,
∴S△BDE=S△EDC,
∵AB∥CD,
∴S△ABD=S△ABC,
∴与△ABD面积相等的三角形有3个,
故选C.
点睛:
本题考查平行线的性质、等高模型等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
9.
解析:
根据“两直线平行,同旁内角互补”解答.
详解:
解:,
.
故答案为:.
点睛:
本题考查平行线的性质定理,熟练掌握定理是解答关键.
10.120
解析:
试题分析:平行线的性质:两直线平行,同旁内角互补.
∵∥,∠1=60°
∴∠2=180°-∠1=120°.
考点:平行线的性质
点评:本题属于基础应用题,只需学生熟练掌握平行线的性质,即可完成.
11.38
解析:
先根据平行线的性质求出∠3的度数,再由余角的定义即可得出结论.
详解:
∵直尺的两边互相平行,∠1=52°,
∴∠3=52°.
∵∠2+∠3=180-90°,
∴∠2=38°.
故答案为:38.
点睛:
本题考查了平行线的性质,熟记性质并准确识图是解题的关键.
12.8
解析:
通过的和底边计算出直线之间的距离,即为的高.
详解:
解:设直线a,b之间的距离为h,则
故答案为:8
点睛:
本题考查了三角形的面积,解题的关键是熟知平行线间的距离处处相等.
13.93°
解析:
连接AC,设∠EAF=x°,∠ECF=y°,则∠EAB=3x°,∠ECD=3y°,可得∠BAF=2x°,∠DCF=2y°,由AB∥CD,三角形的内角和定理,可得∠AFC=2(x°+y°)=62°,计算得到x°+y°=31°,则∠AEC=3(x°+y°),即可得到答案.
详解:
解,如图,连接AC,设∠EAF=x°,∠ECF=y°,
∴∠EAB=3x°,∠ECD=3y°,
∴∠BAF=2x°,∠DCF=2y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠BAF+∠FAC+∠ACF+∠DCF=180°,
∵∠FAC+∠ACF+∠AFC=180°,
∴∠AFC=∠BAF+∠DCF=2(x°+y°)=62°,
∴x°+y°=31°.
同理可求:∠AEC=∠BCE+∠DCE=3(x°+y°),
∴∠AEC=.
故答案为:93°.
点睛:
本题考查了平行线性质和三角形内角和定理的应用,根据题意作出辅助线,构造出三角形,利用三角形内角和定理求解是解答此题的关键.
14.见解析.
解析:
依据AB∥DE,即可得出∠1=∠3,再根据∠1+∠2=180°,即可得到∠3+∠2=180°,进而判定BC∥EF.
详解:
证明:∵AB∥DE,
∴∠1=∠3,
又∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴BC∥EF.
点睛:
本题主要考查了平行线的判定与性质,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
15.见解析
解析:
根据,得到,根据平行线的性质及即可得出,此题得解.
详解:
证明:
.
又
平分.
点睛:
本题考查了平行线的判定与性质以角平分线的定义,熟练掌握平行线的判定与性质定理是解题的关键.
16.(1) AD与EF平行,见解析;(2)
解析:
(1)根据平行线的性质可得,利用等量代换可得,然后根据平行线的判定定理即可证出结论;
(2)先求出,得到,根据平行线的性质即可得到的度数.
详解:
解:(1)AD与EF平行
∵AB∥DG
∴
∵
∴
∴AD∥EF
(2)∵,
∴
∵DG是的平分线
点睛:
此题主要考查平行线的性质及判定,解题的关键是熟知平行线的性质、判定和角平分线的定义.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
5.3.1平行线的性质
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下面四个图形中,与是邻补角的是( )
A. B. C. D.
2.如图,AB // CD,AD=CD,∠1=70°,则∠2的度数是( )
A.40° B.50° C.55° D.60°
3.下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行
B.两直线被第三条直线所截,同旁内角互补
C.不相交的两条直线叫平行线
D.邻补角的平分线互相垂直
4.如图,Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,若∠BCE=35°,则∠A的度数为( )
A. B. C. D.
5.如图,将一张含有角的三角形纸片的两个顶点放在直尺的两条对边上,若,则的度数是( )
A. B. C. D.
6.如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2的度数是( )
A.55° B.65° C.75° D.85°
7.如图,AB∥CD,DE⊥CE,∠1=36°,则∠DCE的度数为( )
A.36° B.44° C.66° D.54°
8.如图,AB∥DC,ED∥BC,AE∥BD,那么图中与△ABD面积相等的三角形有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,直线,直线与直线,都相交.若,则_______.
10.如右图,已知直线、被直线所截,∠1=60°, 则当∠2= °时,∥.
11.如图,把一个直角三角尺的直角顶点放在直尺的一边上,若∠1=52°,则∠2= _______°.
12. 如图,已知直线,点C,D在直线a上,点在直线b上,线段相交于点E,若的面积为,,,则的面积为?_______________________?.
13.如图,已知AB∥CD,∠EAF =∠EAB,∠ECF=∠ECD ,∠AFC=62°,则∠AEC度数是________
三、解答题
14.如图,,,试说明:.
15.如图所示:已知,,试说明平分.
16.如图,AB∥DG,,
1)问:AD与EF平行吗?请说明理由;
2)若DG是的平分线,,求的度数.
参考答案
1.C
解析:
根据邻补角的定义,相邻且互补的两个角互为邻补角进行判断.
详解:
解:A、B选项,∠1与∠2没有公共顶点且不相邻,不是邻补角;
C选项互补且相邻,是邻补角;
D选项∠1与∠2不互补,不是邻补角;
故选C.
点睛:
本题考查邻补角的定义,是一个需要熟记的内容.
2.A
解析:
先根据平行线的性质求出∠ACD的度数,再由AC=CD得出∠CAD的度数,根据三角形内角和定理即可得出结论.
详解:
解:∵AB∥CD,∠1=70°,
∴∠ACD=∠1=70°.
∵AD=CD,
∴∠CAD=∠ACD=70°,
∴∠2=180°-∠ACD-∠CAD=180°-70°-70°=40°.
故选:A.
点睛:
本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.
3.D
解析:A选项正确说法应该是:过直线外一点有且只有一条直线与已知直线平行,故是错误的;
B选项正确说法应该是:两条平行线被第三条直线所截,同旁内角互补,故是错误的;
C选项正确说法应该是:在同一平面内,不相交的两条直线叫平行线,故是错误的;
D选项是正解的;
故选D。
4.C
解析:
分析:题中有三个条件,图形为常见图形,可先由AB∥DE,∠BCE=35°,根据两直线平行,内错角相等求出∠B,然后根据三角形内角和为180°求出∠A.
详解:∵AB∥DE,∠BCE=35°,∴∠B=∠BCE=35°(两直线平行,内错角相等).
又∵∠ACB=90°,∴∠A=90°﹣35°=55°(在直角三角形中,两个锐角互余).
故选C.
点睛:看到两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.
5.C
解析:
利用平行线的性质,三角形的外角的性质解决问题即可;
详解:
解:如图,
∵AB∥CD,
∴∠3=∠2,
∴∠3=∠1+30°,
∵∠1=20°,
∴∠3=∠2=50°;
故选:C.
点睛:
本题主要考查平行线的性质,三角形的外角等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
6.B
解析:
根据两直线平行,同旁内角互补可求出∠AFD的度数,然后根据对顶角相等求出∠2的度数.
详解:
∵AB∥CD,
∴∠1+∠AFD=180°,
∵∠1=115°,
∴∠AFD=65°,
∵∠2和∠AFD是对顶角,
∴∠2=∠AFD=65°,
故选B.
点睛:
本题主要考查了平行线的性质,解题的关键是掌握两直线平行,同旁内角互补.
7.D
解析:
∵DE⊥CE,
∴∠CED=90?,
∴∠BEC=180 ?-90 ?-36 ?=54 ?.
∵AB∥CD,
∴∠DCE=∠BEC=54 ?.
故选D.
8.C
解析:
根据等高模型,同底等高的三角形的面积相等即可判断;
详解:
解:∵AE∥BD,
∴S△ABD=S△BDE,
∵DE∥BC,
∴S△BDE=S△EDC,
∵AB∥CD,
∴S△ABD=S△ABC,
∴与△ABD面积相等的三角形有3个,
故选C.
点睛:
本题考查平行线的性质、等高模型等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
9.
解析:
根据“两直线平行,同旁内角互补”解答.
详解:
解:,
.
故答案为:.
点睛:
本题考查平行线的性质定理,熟练掌握定理是解答关键.
10.120
解析:
试题分析:平行线的性质:两直线平行,同旁内角互补.
∵∥,∠1=60°
∴∠2=180°-∠1=120°.
考点:平行线的性质
点评:本题属于基础应用题,只需学生熟练掌握平行线的性质,即可完成.
11.38
解析:
先根据平行线的性质求出∠3的度数,再由余角的定义即可得出结论.
详解:
∵直尺的两边互相平行,∠1=52°,
∴∠3=52°.
∵∠2+∠3=180-90°,
∴∠2=38°.
故答案为:38.
点睛:
本题考查了平行线的性质,熟记性质并准确识图是解题的关键.
12.8
解析:
通过的和底边计算出直线之间的距离,即为的高.
详解:
解:设直线a,b之间的距离为h,则
故答案为:8
点睛:
本题考查了三角形的面积,解题的关键是熟知平行线间的距离处处相等.
13.93°
解析:
连接AC,设∠EAF=x°,∠ECF=y°,则∠EAB=3x°,∠ECD=3y°,可得∠BAF=2x°,∠DCF=2y°,由AB∥CD,三角形的内角和定理,可得∠AFC=2(x°+y°)=62°,计算得到x°+y°=31°,则∠AEC=3(x°+y°),即可得到答案.
详解:
解,如图,连接AC,设∠EAF=x°,∠ECF=y°,
∴∠EAB=3x°,∠ECD=3y°,
∴∠BAF=2x°,∠DCF=2y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠BAF+∠FAC+∠ACF+∠DCF=180°,
∵∠FAC+∠ACF+∠AFC=180°,
∴∠AFC=∠BAF+∠DCF=2(x°+y°)=62°,
∴x°+y°=31°.
同理可求:∠AEC=∠BCE+∠DCE=3(x°+y°),
∴∠AEC=.
故答案为:93°.
点睛:
本题考查了平行线性质和三角形内角和定理的应用,根据题意作出辅助线,构造出三角形,利用三角形内角和定理求解是解答此题的关键.
14.见解析.
解析:
依据AB∥DE,即可得出∠1=∠3,再根据∠1+∠2=180°,即可得到∠3+∠2=180°,进而判定BC∥EF.
详解:
证明:∵AB∥DE,
∴∠1=∠3,
又∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴BC∥EF.
点睛:
本题主要考查了平行线的判定与性质,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
15.见解析
解析:
根据,得到,根据平行线的性质及即可得出,此题得解.
详解:
证明:
.
又
平分.
点睛:
本题考查了平行线的判定与性质以角平分线的定义,熟练掌握平行线的判定与性质定理是解题的关键.
16.(1) AD与EF平行,见解析;(2)
解析:
(1)根据平行线的性质可得,利用等量代换可得,然后根据平行线的判定定理即可证出结论;
(2)先求出,得到,根据平行线的性质即可得到的度数.
详解:
解:(1)AD与EF平行
∵AB∥DG
∴
∵
∴
∴AD∥EF
(2)∵,
∴
∵DG是的平分线
点睛:
此题主要考查平行线的性质及判定,解题的关键是熟知平行线的性质、判定和角平分线的定义.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
