10.2直方图 同步练习 (含详解)
图片预览



文档简介
小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
10.2直方图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列六个数:0、、、、-、中,无理数出现的频数是( ).
A.3 B.4 C.5 D.6
2.超市为了制定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间6分钟到7分钟表示>或等于6分钟而<7分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为 ( )
A.5 B.7 C.16 D.33
3.如图是杭州市区人口的统计图,则根据统计图得出的下列判断正确的是( )
A.其中有3个区的人口数都低于40万
B.只有1个区的人口数超过百万
C.上城区与下城区的人口之和超过江干区的人口数
D.杭州市区的人口数已超过600万
4.某同学统计了他家今年10月份打电话的次数及地时间,并列出了频数分布表:
通话区时间x(分钟)
通话频数(次数) 21 14 8 5 2
通话时间超过10分钟的频率是( )
A.0.28 B.0.3 C.0.5 D.0.7
5.某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )
A.得分在70~80分的人数最多 B.该班的总人数为40
C.人数最少的得分段的频数为2 D.得分及格(≥60分)的有12人
6.要反映台州市某一周每天的最高气温的变化趋势,宜采用( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.频数分布统计图
7.如图是某班一次数学测试成绩的频数直方图,则成绩在69.5~89.5分范围内的学生共有( )
A.24人 B.10人 C.14人 D.29人
8.某班有64位同学,在一次数学检测中,分数只能取整数,统计其成绩绘制成频数直方图,如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则由图可知,其中分数在70.5~80.5之间的人数是( )
A.12 B.24 C.16 D.8
二、填空题
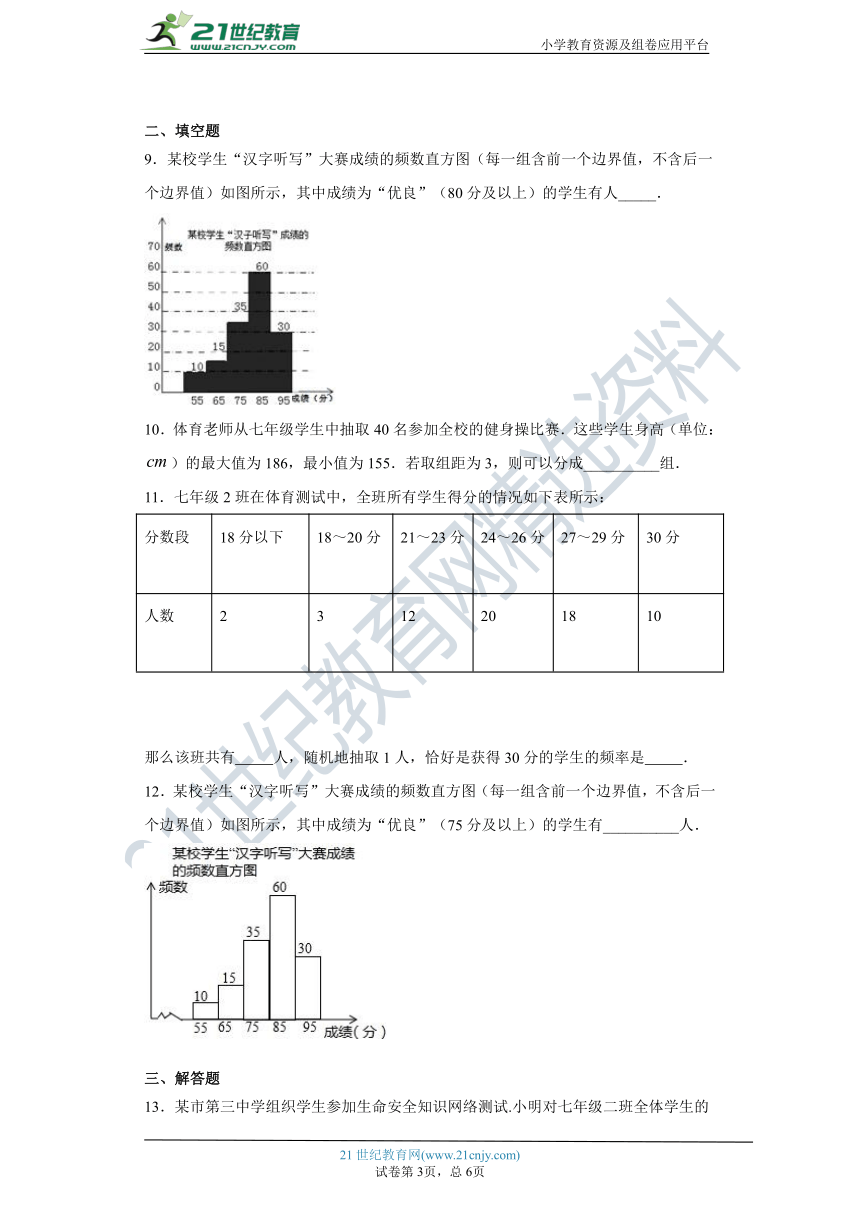
9.某校学生“汉字听写”大赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩为“优良”(80分及以上)的学生有人_____.
10.体育老师从七年级学生中抽取40名参加全校的健身操比赛.这些学生身高(单位:)的最大值为186,最小值为155.若取组距为3,则可以分成__________组.
11.七年级2班在体育测试中,全班所有学生得分的情况如下表所示:
分数段
18分以下
18~20分
21~23分
24~26分
27~29分
30分
人数
2
3
12
20
18
10
那么该班共有 人,随机地抽取1人,恰好是获得30分的学生的频率是 .
12.某校学生“汉字听写”大赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩为“优良”(75分及以上)的学生有__________人.
三、解答题
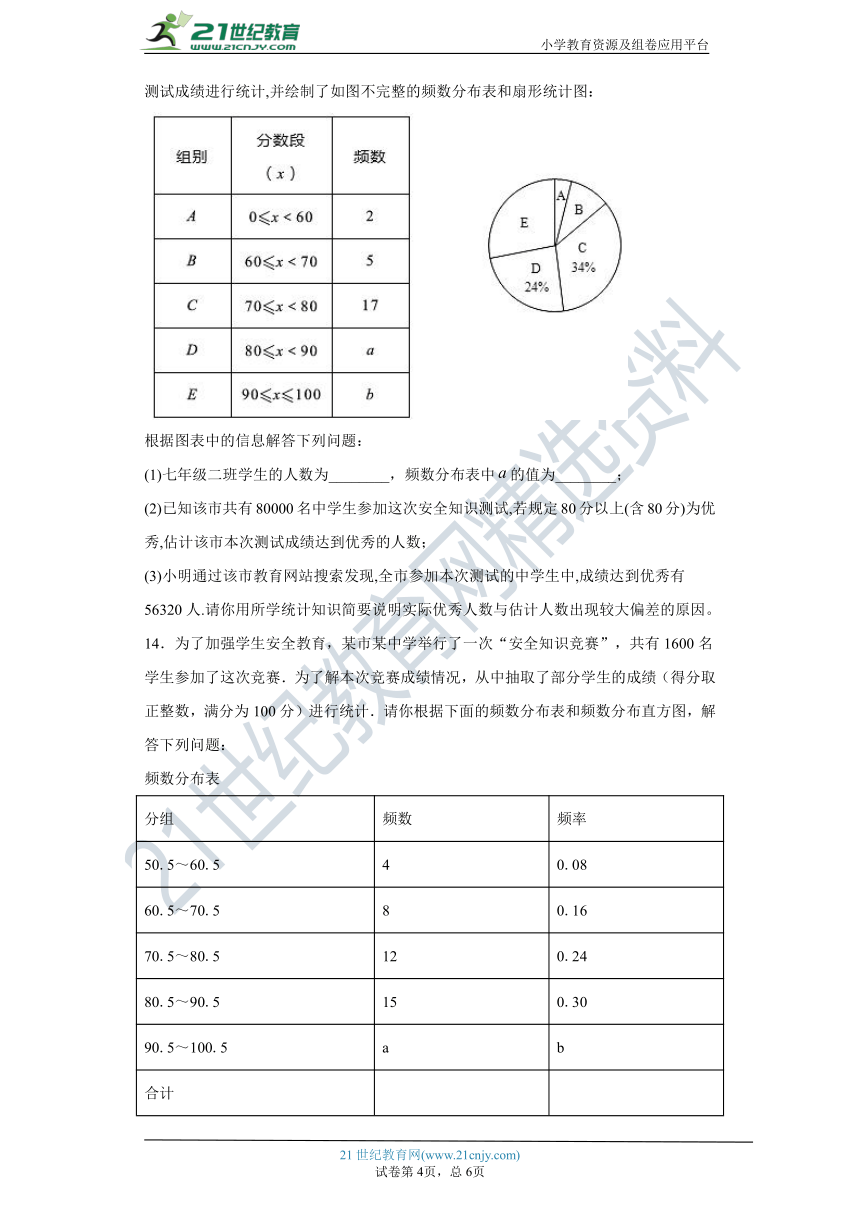
13.某市第三中学组织学生参加生命安全知识网络测试.小明对七年级二班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图:
根据图表中的信息解答下列问题:
(1)七年级二班学生的人数为________,频数分布表中的值为________;
(2)已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上(含80分)为优秀,佔计该市本次测试成绩达到优秀的人数;
(3)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因。
14.为了加强学生安全教育,某市某中学举行了一次“安全知识竞赛”,共有1600名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面的频数分布表和频数分布直方图,解答下列问题:
频数分布表
分组 频数 频率
50.5~60.5 4 0.08
60.5~70.5 8 0.16
70.5~80.5 12 0.24
80.5~90.5 15 0.30
90.5~100.5 a b
合计
(1)频数分布表中a= ,b= ;
(2)抽取的样本容量是 ,请补全频数分布直方图.
(3)若成绩在80分以上(不含80分)为优秀,则该校成绩没达到优秀的约为多少人?
15.某学校随机抽取部分学生,调查每个月的零花钱消费额,数据整理成如下的统计表和如图①②所示的两幅不完整的统计图,已知图①中A,E两组对应的小长方形的高度之比为2:1请结合相关数据解答以下问题:
(1)本次调查样本的容量是______;
(2)补全频数分布直方图,并标明各组的频数;
(3)若该学校有2500名学生,请估计月消费零花钱不少于300元的学生的数量.
16.2019年4月23日是第24个世界读书日. 习近平总书记说:“读书可以让人保持思想活力让人得到智慧启发,让人滋养浩然之气”. 厦门市某中学响应号召,创造有利条件,鼓励学生利用课余时间广泛阅读. 学校文学社想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间(小时)进行分组整理,并绘制了下面不完整的频数分布直方图和扇形统计图. 根捷图中提供的信息,解答下列问题:
(1)这次抽样调查的学生人数是 人;
(2)扇形统计图中“”组对应的圆心角度数为 ,并将频数分布直方图补充完整;
(3)若该校有1200名学生,请估计全校有多少名学生每周的课外阅读时间不少于6小时?
参考答案
1.A
解析:
根据无理数的概念即可作答.
详解:
解:∵其中无理数有:,,;∴无理数出现的频数是3,
故选:A.
点睛:
本题考查无理数的概念,是中考的常考题,掌握无理数的内涵是基础.
2.B
解析:
由频数直方图可以看出:最后两组顾客等待时间不少于6分钟,人数为5+2=7.
3.D
解析:
A.只有上城区人口数低于40万,故此选项错误;B.萧山区、余杭区两个区的人口超过100万,故此选项错误;C.上城区与下城区的人口数之和低于江干区的人口数,故此选项错误;D.杭州市区的人口数已超过600万,故此选项正确.
4.B
解析:
根据频率计算公式,频率等于频数与数据总数的比即可求解.
详解:
通话时间超过10分钟的频率为:
故选:B
点睛:
本题主要掌握观察频数分布表,考查了频率计算公式,频率等于频数与数据总数的比.
5.D
解析:
试题分析:A、得分在70~80分之间的人数最多,有14人,此选项正确;
B、该班的总人数为4+12+14+8+2=40人,此选项正确;
C、得分在90~100分之间的人数最少,有2人,频数为2,此选项正确;
D、及格(≥60分)人数是12+14+8+2=36人,此选项错误.
故选D.
点睛:本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
6.C
解析:
根据题意,得
要求直观反映长沙市一周内每天的最高气温的变化情况,结合统计图各自的特点,应选择折线统计图.
故选C.
7.A
解析:
根据直方图给出的数据,把成绩在分范围内的学生人数相加即可得出答案.
详解:
解:成绩在分范围内的学生共有:人,
故选A.
点睛:
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
8.B
解析:
小长方形的高度比等于各组的人数比,即可求得分数在70.5到80.5之间的人数所占的比例,乘以总数64即可得出答案.
详解:
分数在70.5到80.5之间的人数是:×64=24(人).
故选B.
点睛:
本题考查了频数分布直方图,了解频数分布直方图中小长方形的高度比与各组人数比的关系是解答问题的关键.
9.90
解析:
根据条形统计图可以得到80分及以上的学生人数.
详解:
解:80分及以上的学生有:60+30=90人,
故答案为:90.
点睛:
此题考查了频数(率)分布直方图,以及利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能做出正确的判断并解决问题.
10.11
解析:
计算最大值与最小值的差,除以组距即可求得.
详解:
解:∵极差为:186-155=31,且组距为3,
则组数为31÷3≈11(组),
故答案为:11.
点睛:
此题考查的是组数的确定方法,掌握组数=极差÷组距是关键.
11.65;.
解析:
试题解析:根据统计表的意义,该班共有2+3+12+20+18+10=65人,
读表可得:恰好是获得30分的学生有10人,则其频率为.
考点:频数与频率.
12.125
解析:
根据条形统计图可以得到75分及以上的学生人数.
详解:
75分及以上的学生有:35+60+30=125人,
故答案为125.
点睛:
此题考查了频数(率)分布直方图,以及利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能做出正确的判断并解决问题.
13.(1) 50人,a=12;(2) 41600人;(3)见解析.
解析:
(1)根据数据总数=代入计算,求出七年级2班学生的人数;
(2)先计算优秀的百分比,再与80000相乘即可;
(3)取的样本不足以代表全市总中学的总体情况.
详解:
解:(1)17÷34%=50(人),a=24%×50=12,
答:九年级2班学生的人数为50人;
(2)E:14÷50=28%,
(28%+24%)×80000=52×800=41600(人),
答:估计该市本次测试成绩达到优秀的人数为41600人;
(3)全市参加本次测试的中学生中,成绩达到优秀有56?320人;而样本中估计该市本次测试成绩达到优秀的人数为41600人,原因是:小明对第三中学九年2班全体学生的测试成绩取的样本不足以代表全市总中学的总体情况,所以会出现较大偏差.
点睛:
本题考查了数据的收集与整理,根据频数分布表和扇形统计图可以将大量数据分类,结果清晰,一目了然地表达出来,熟练掌握公式是做好本题的关键:数据总数=,各组频数和=总数据.
14.(1)11,0.22;(2)50,见解析;(3)该校成绩没达到优秀的约为768人.
解析:
(1)根据第一组的频数与频率列式求出被抽取的学生总人数,然后减去其它各组的人数即可得到a的值,用a的值除以总人数即可得到b;
(2)根据(1)的计算可得抽取的样本容量是50,并且补全直方图即可;
(3)用学生总人数乘以前三组的频率之和,计算即可得解.
详解:
(1)被抽取的学生人数为:4÷0.08=50(人),
所以,a=50﹣4﹣8﹣12﹣15=50﹣39=11,
b==0.22;
故答案为11;0.22.
(2)由(1)可知,抽取的样本容量是50.
补全频数分布直方图如图所示:
故答案为50;
(3)(0.08+0.16+0.24)×1600=768(人).
答:该校成绩没达到优秀的约为768人.
点睛:
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
15.(1)100;(2)见解析;(3)750
解析:
(1)(2)根据样本容量、频数、频率的关系进行求解;(3)根据频率估计概率进行求解.
详解:
(1)由图①中A,E两组对应的小长方形的高度之比为2:1,可得E组的频数为5,则A组和E组的频数之和为15,由图②可知,A组和E组的频率为15%,则样本容量为.
(2)由样本容量和图②中各组的频率,可知各组的频数依次为:10、20、40、25、5,则频数分布直方图如下:
(3)月消费零花钱不少于300元的学生是调查样本中D组和E组代表的学生,总频率为30%,根据频率估计概率,则该学校有2500名学生有30%的学生月消费零花钱不少于300元,即750名学生.
点睛:
本题考查了样本容量、频数、频率的关系,以及根据频率估计概率.
16.(1)50;(2)108°,图详见解析;(3)全校有288名学生每周的课外阅读时间不少于6小时
解析:
(1)根据B部分的频数和所占的百分比可以求得本次调查的人数;
(2)根据(1)中的结果和频数分布直方图中的数据可以求得A部分和C部分的频数,从而可以解答本题;
(3)根据直方图中的数据可以求得全校有多少名学生每周的课外阅读时间不少于6小时.
详解:
(1)本次抽查的学生有:18÷36%=50(人),
故答案为:50;
(2)A部分的频数是50×10%=5,
扇形统计图中“C”组对应的圆心角度数为: ,
故答案为:108°,
C部分的人数为: ,
补全的频数分布直方图如右图所示;
(3) (名),
答:全校有288名学生每周的课外阅读时间不少于6小时.
点睛:
本题考查频数分布直方图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
10.2直方图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列六个数:0、、、、-、中,无理数出现的频数是( ).
A.3 B.4 C.5 D.6
2.超市为了制定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间6分钟到7分钟表示>或等于6分钟而<7分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为 ( )
A.5 B.7 C.16 D.33
3.如图是杭州市区人口的统计图,则根据统计图得出的下列判断正确的是( )
A.其中有3个区的人口数都低于40万
B.只有1个区的人口数超过百万
C.上城区与下城区的人口之和超过江干区的人口数
D.杭州市区的人口数已超过600万
4.某同学统计了他家今年10月份打电话的次数及地时间,并列出了频数分布表:
通话区时间x(分钟)
通话频数(次数) 21 14 8 5 2
通话时间超过10分钟的频率是( )
A.0.28 B.0.3 C.0.5 D.0.7
5.某班级的一次数学考试成绩统计图如图,则下列说法错误的是( )
A.得分在70~80分的人数最多 B.该班的总人数为40
C.人数最少的得分段的频数为2 D.得分及格(≥60分)的有12人
6.要反映台州市某一周每天的最高气温的变化趋势,宜采用( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.频数分布统计图
7.如图是某班一次数学测试成绩的频数直方图,则成绩在69.5~89.5分范围内的学生共有( )
A.24人 B.10人 C.14人 D.29人
8.某班有64位同学,在一次数学检测中,分数只能取整数,统计其成绩绘制成频数直方图,如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则由图可知,其中分数在70.5~80.5之间的人数是( )
A.12 B.24 C.16 D.8
二、填空题
9.某校学生“汉字听写”大赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩为“优良”(80分及以上)的学生有人_____.
10.体育老师从七年级学生中抽取40名参加全校的健身操比赛.这些学生身高(单位:)的最大值为186,最小值为155.若取组距为3,则可以分成__________组.
11.七年级2班在体育测试中,全班所有学生得分的情况如下表所示:
分数段
18分以下
18~20分
21~23分
24~26分
27~29分
30分
人数
2
3
12
20
18
10
那么该班共有 人,随机地抽取1人,恰好是获得30分的学生的频率是 .
12.某校学生“汉字听写”大赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩为“优良”(75分及以上)的学生有__________人.
三、解答题
13.某市第三中学组织学生参加生命安全知识网络测试.小明对七年级二班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图:
根据图表中的信息解答下列问题:
(1)七年级二班学生的人数为________,频数分布表中的值为________;
(2)已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上(含80分)为优秀,佔计该市本次测试成绩达到优秀的人数;
(3)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因。
14.为了加强学生安全教育,某市某中学举行了一次“安全知识竞赛”,共有1600名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面的频数分布表和频数分布直方图,解答下列问题:
频数分布表
分组 频数 频率
50.5~60.5 4 0.08
60.5~70.5 8 0.16
70.5~80.5 12 0.24
80.5~90.5 15 0.30
90.5~100.5 a b
合计
(1)频数分布表中a= ,b= ;
(2)抽取的样本容量是 ,请补全频数分布直方图.
(3)若成绩在80分以上(不含80分)为优秀,则该校成绩没达到优秀的约为多少人?
15.某学校随机抽取部分学生,调查每个月的零花钱消费额,数据整理成如下的统计表和如图①②所示的两幅不完整的统计图,已知图①中A,E两组对应的小长方形的高度之比为2:1请结合相关数据解答以下问题:
(1)本次调查样本的容量是______;
(2)补全频数分布直方图,并标明各组的频数;
(3)若该学校有2500名学生,请估计月消费零花钱不少于300元的学生的数量.
16.2019年4月23日是第24个世界读书日. 习近平总书记说:“读书可以让人保持思想活力让人得到智慧启发,让人滋养浩然之气”. 厦门市某中学响应号召,创造有利条件,鼓励学生利用课余时间广泛阅读. 学校文学社想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间(小时)进行分组整理,并绘制了下面不完整的频数分布直方图和扇形统计图. 根捷图中提供的信息,解答下列问题:
(1)这次抽样调查的学生人数是 人;
(2)扇形统计图中“”组对应的圆心角度数为 ,并将频数分布直方图补充完整;
(3)若该校有1200名学生,请估计全校有多少名学生每周的课外阅读时间不少于6小时?
参考答案
1.A
解析:
根据无理数的概念即可作答.
详解:
解:∵其中无理数有:,,;∴无理数出现的频数是3,
故选:A.
点睛:
本题考查无理数的概念,是中考的常考题,掌握无理数的内涵是基础.
2.B
解析:
由频数直方图可以看出:最后两组顾客等待时间不少于6分钟,人数为5+2=7.
3.D
解析:
A.只有上城区人口数低于40万,故此选项错误;B.萧山区、余杭区两个区的人口超过100万,故此选项错误;C.上城区与下城区的人口数之和低于江干区的人口数,故此选项错误;D.杭州市区的人口数已超过600万,故此选项正确.
4.B
解析:
根据频率计算公式,频率等于频数与数据总数的比即可求解.
详解:
通话时间超过10分钟的频率为:
故选:B
点睛:
本题主要掌握观察频数分布表,考查了频率计算公式,频率等于频数与数据总数的比.
5.D
解析:
试题分析:A、得分在70~80分之间的人数最多,有14人,此选项正确;
B、该班的总人数为4+12+14+8+2=40人,此选项正确;
C、得分在90~100分之间的人数最少,有2人,频数为2,此选项正确;
D、及格(≥60分)人数是12+14+8+2=36人,此选项错误.
故选D.
点睛:本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
6.C
解析:
根据题意,得
要求直观反映长沙市一周内每天的最高气温的变化情况,结合统计图各自的特点,应选择折线统计图.
故选C.
7.A
解析:
根据直方图给出的数据,把成绩在分范围内的学生人数相加即可得出答案.
详解:
解:成绩在分范围内的学生共有:人,
故选A.
点睛:
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
8.B
解析:
小长方形的高度比等于各组的人数比,即可求得分数在70.5到80.5之间的人数所占的比例,乘以总数64即可得出答案.
详解:
分数在70.5到80.5之间的人数是:×64=24(人).
故选B.
点睛:
本题考查了频数分布直方图,了解频数分布直方图中小长方形的高度比与各组人数比的关系是解答问题的关键.
9.90
解析:
根据条形统计图可以得到80分及以上的学生人数.
详解:
解:80分及以上的学生有:60+30=90人,
故答案为:90.
点睛:
此题考查了频数(率)分布直方图,以及利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能做出正确的判断并解决问题.
10.11
解析:
计算最大值与最小值的差,除以组距即可求得.
详解:
解:∵极差为:186-155=31,且组距为3,
则组数为31÷3≈11(组),
故答案为:11.
点睛:
此题考查的是组数的确定方法,掌握组数=极差÷组距是关键.
11.65;.
解析:
试题解析:根据统计表的意义,该班共有2+3+12+20+18+10=65人,
读表可得:恰好是获得30分的学生有10人,则其频率为.
考点:频数与频率.
12.125
解析:
根据条形统计图可以得到75分及以上的学生人数.
详解:
75分及以上的学生有:35+60+30=125人,
故答案为125.
点睛:
此题考查了频数(率)分布直方图,以及利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能做出正确的判断并解决问题.
13.(1) 50人,a=12;(2) 41600人;(3)见解析.
解析:
(1)根据数据总数=代入计算,求出七年级2班学生的人数;
(2)先计算优秀的百分比,再与80000相乘即可;
(3)取的样本不足以代表全市总中学的总体情况.
详解:
解:(1)17÷34%=50(人),a=24%×50=12,
答:九年级2班学生的人数为50人;
(2)E:14÷50=28%,
(28%+24%)×80000=52×800=41600(人),
答:估计该市本次测试成绩达到优秀的人数为41600人;
(3)全市参加本次测试的中学生中,成绩达到优秀有56?320人;而样本中估计该市本次测试成绩达到优秀的人数为41600人,原因是:小明对第三中学九年2班全体学生的测试成绩取的样本不足以代表全市总中学的总体情况,所以会出现较大偏差.
点睛:
本题考查了数据的收集与整理,根据频数分布表和扇形统计图可以将大量数据分类,结果清晰,一目了然地表达出来,熟练掌握公式是做好本题的关键:数据总数=,各组频数和=总数据.
14.(1)11,0.22;(2)50,见解析;(3)该校成绩没达到优秀的约为768人.
解析:
(1)根据第一组的频数与频率列式求出被抽取的学生总人数,然后减去其它各组的人数即可得到a的值,用a的值除以总人数即可得到b;
(2)根据(1)的计算可得抽取的样本容量是50,并且补全直方图即可;
(3)用学生总人数乘以前三组的频率之和,计算即可得解.
详解:
(1)被抽取的学生人数为:4÷0.08=50(人),
所以,a=50﹣4﹣8﹣12﹣15=50﹣39=11,
b==0.22;
故答案为11;0.22.
(2)由(1)可知,抽取的样本容量是50.
补全频数分布直方图如图所示:
故答案为50;
(3)(0.08+0.16+0.24)×1600=768(人).
答:该校成绩没达到优秀的约为768人.
点睛:
本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
15.(1)100;(2)见解析;(3)750
解析:
(1)(2)根据样本容量、频数、频率的关系进行求解;(3)根据频率估计概率进行求解.
详解:
(1)由图①中A,E两组对应的小长方形的高度之比为2:1,可得E组的频数为5,则A组和E组的频数之和为15,由图②可知,A组和E组的频率为15%,则样本容量为.
(2)由样本容量和图②中各组的频率,可知各组的频数依次为:10、20、40、25、5,则频数分布直方图如下:
(3)月消费零花钱不少于300元的学生是调查样本中D组和E组代表的学生,总频率为30%,根据频率估计概率,则该学校有2500名学生有30%的学生月消费零花钱不少于300元,即750名学生.
点睛:
本题考查了样本容量、频数、频率的关系,以及根据频率估计概率.
16.(1)50;(2)108°,图详见解析;(3)全校有288名学生每周的课外阅读时间不少于6小时
解析:
(1)根据B部分的频数和所占的百分比可以求得本次调查的人数;
(2)根据(1)中的结果和频数分布直方图中的数据可以求得A部分和C部分的频数,从而可以解答本题;
(3)根据直方图中的数据可以求得全校有多少名学生每周的课外阅读时间不少于6小时.
详解:
(1)本次抽查的学生有:18÷36%=50(人),
故答案为:50;
(2)A部分的频数是50×10%=5,
扇形统计图中“C”组对应的圆心角度数为: ,
故答案为:108°,
C部分的人数为: ,
补全的频数分布直方图如右图所示;
(3) (名),
答:全校有288名学生每周的课外阅读时间不少于6小时.
点睛:
本题考查频数分布直方图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
