26.2实际问题与反比例函数 同步练习(含详解)
文档属性
| 名称 | 26.2实际问题与反比例函数 同步练习(含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
26.2实际问题与反比例函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲、乙两地相距250千米,如果把汽车从甲地到乙地所用的时间y(小时),表示为汽车的平均速度为x(千米/小时)的函数,则此函数的图象大致是( ).
A. B.
C.D.
2.某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A.(x>0) B.(x≥0) C.y=300x(x≥0) D.y=300x(x>0)
3.一个圆柱的侧面展开图是一个面积为4平方单位的矩形,那么这个圆柱的母线长L和底面半径r之间的函数关系是
A.反比例函数 B.正比例函数 C.一次函数 D.二次函数
4.在公式ρ=中,当质量m一定时,密度与体积V之间的函数关系可用图象表示为( )
A. B. C.D.
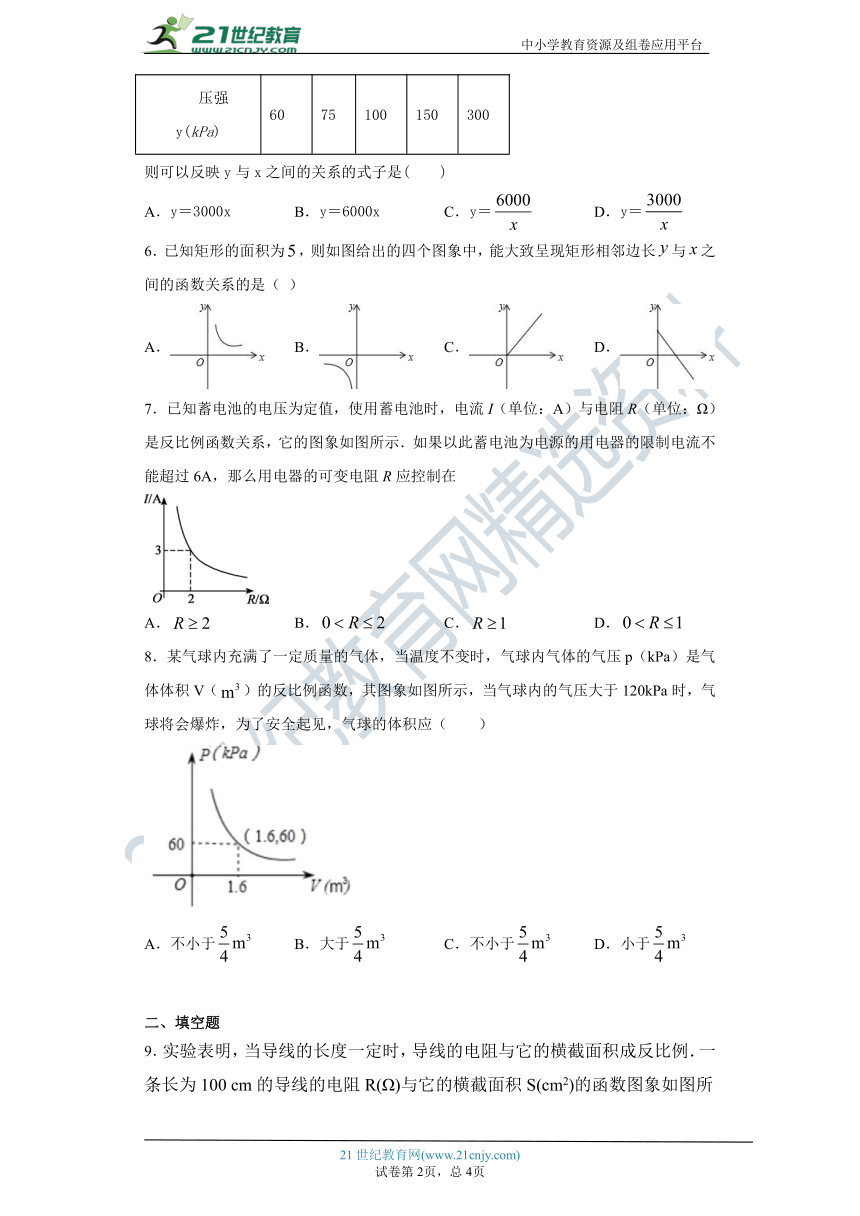
5.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:
体积x(mL) 100 80 60 40 20
压强y(kPa) 60 75 100 150 300
则可以反映y与x之间的关系的式子是( )
A.y=3000x B.y=6000x C.y= D.y=
6.已知矩形的面积为,则如图给出的四个图象中,能大致呈现矩形相邻边长与之间的函数关系的是( )
A. B. C. D.
7.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.如果以此蓄电池为电源的用电器的限制电流不能超过6A,那么用电器的可变电阻R应控制在
A. B. C. D.
8.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V()的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将会爆炸,为了安全起见,气球的体积应( )
A.不小于 B.大于 C.不小于 D.小于
二、填空题
9.实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100 cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为___________,当S=2 cm2时, R=______________(Ω)
10.利用数学公式可建立反比例函数关系式,圆柱体的容积=_______×___.
11.三角形的面积是,它的底边(单位:)与这个底边上的高(单位:)的函数关系式为________.
12.已知△ABC的三个顶点为A(-1,1),B(-1,3),C(-3,-3),将△ABC向右平移m(m>0)个单位后,△ABC某一边的中点恰好落在反比例函数y= 的图象上,则m的值为________.
三、解答题
13.一个面积为42的长方形,其相邻两边长分别为x和y,请你写出与之间的函数解析式,并画出其图象.
14.“聚能”电厂现在有5000吨煤.
(1)求:这些煤能够使用的天数x(单位:天)与该厂平均每天用煤吨数y(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批煤能用多少天?
(3)若该电厂前10天每天用煤200吨,后因各地用电紧张,每天用煤300吨,则这批煤共可用多少天?
15.(1)在所给平面直角坐标系中,画出反比例函数的图象;
(2)函数的图象是轴对称图形吗?有几条对称轴?
(3)上述图象的两个分支是否成中心对称,请指出对称中心,并写出两对对称点坐标.
16.某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价(元)与日销售量(个)之间有如下关系:
日销售单价(元) 3 4 5 6
日销售量(个) 20 15 12 10
(1)根据表中数据,在直角坐标系中描出实数对的对应点;
(2)猜测并确定与之间的函数关系式,并画出图像;
(3)设经营此贺卡的销售利润为元,求出与之间的函数关系式. 若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价定为多少时,才能获得最大日销售利润?
参考答案
1.D
解析:本题考查的是函数图象
根据路程、速度、时间三个量之间的关系即可得到结论.
由题意得,故选D.
2.A
解析:由“这批煤燃烧的天数=这批煤的总量÷每天烧煤的吨数”可得:
.
故选A.
3.A
解析:试题解析:根据题意,得2πrL=4,
则
所以这个圆柱的母线长L和底面半径r之间的函数关系是反比例函数.
故选A.
4.B
解析:∵在公式ρ=中,且质量m一定,
∴是v的反比例函数,且图象在第一象限.
故选B.
5.C
解析:
利用表格中数据得出函数关系,进而求出即可.
详解:
解:此函数是反比例函数,设解析式为:y=,则xy=k=6000,
故y与x之间的关系是y=.
故选C.
点睛:
此题主要考查了根据实际问题列反比例函数关系式.
6.A
解析:
根据矩形的面积公式得出xy=5,那么y与x之间的函数关系为反比例函数关系,再根据x、y所表示的实际意义得到x、y应大于0;即可得出答案.
详解:
∵矩形的面积为5,矩形相邻的两边长分别是y与x,
∴xy=5,
∴(x>0,y>0),
故选:A.
点睛:
考查反比例函数的应用,解答该类题目的关键是确定两个变量之间的函数关系,利用实际意义确定所在的象限.
7.C
解析:
根据题意首先求出反比例函数解析式,进而利用电器的限制不能超过12A,求出电器的可变电阻应控制的范围.
详解:
设反比例函数关系式为:I=,
把(2,3)代入得:k=2×3=6,
∴反比例函数关系式为:I=,
当I≤6时,则≤6,
R≥1,
故选:C.
点睛:
此题主要考查了反比例函数的应用,正确得出反比例函数解析式是解题关键.
8.C
解析:
由题意设设,把(1.6,60)代入得到k=96,推出,当P=120时,,由此即可判断.
详解:
因为气球内气体的气压p(kPa)是气体体积V()的反比例函数,所以可设,由题图可知,当时,,所以,所以.为了安全起见,气球内的气压应不大于120kPa,即,所以.
故选C.
点睛:
此题考查反比例函数的应用,解题关键在于把已知点代入解析式.
9.R= 14.5
解析:设反比例函数解析式为:R= ,
将(1,29)代入得:k=29,
则其函数关系式为:R= ,
当S=2cm2时,R==14.5(Ω).
故答案是:R=,14.5.
10. 底面积 高
【解析】圆柱的体积公式为:圆柱体的容积=底面积×高.
11.
解析:
根据等量关系“三角形的面积=底边底边上的高” 即可列出a与h的关系式.
详解:
解:由题意得a=220h=
故答案为:
点睛:
本题考查了反比例函数在实际生活中的应用,找出等量关系是解决此题的关键.
12.
解析:
根据中点的坐标和平移的规律,利用点在函数图像上,可解出m的值.
详解:
△ABC的三个顶点为A(-1,1),B(-1,3),C(-3,3)
∴AB的中点(-1,2),BC的中点(-2,0),AC的中点(-2,-1)
∴AB边的中点平移后为(-1+m,2),AC中点平移后为(-2+m,-1)
∵△ABC某一边中点落在反比例函数上
∴2(-1+m)=3或-1×(-2+m)=3
m=2.5或-1(舍去).
故答案是:.
点睛:
考查了反比例函数图象上点的坐标特点,关键是掌握反比例函数图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
13.y=,图象见解析.
解析:本题考查的是根据实际问题列函数关系式
根据长方形的面积公式可得其解析式,再用描点法画出其图象即可.
由题意得,函数解析式为,图象略.
14.(1)y=.(2)这批电煤能用25天.(3) 共可用20天.
解析:试题分析:(1)根据平均每天用煤吨数=总电煤 使用的天数列式;(2)当x=200代入反比例函数中计算即可;(3)先求出前10天剩余的电煤量,再除以300即可求出;
试题解析:
(1)y=.
(2)把x=200代入y=,
得y=25.
故这批电煤能用25天.
(3)前10天后还剩下5000-10×200=3000(吨)电煤,可以用=10(天),故共可用20天.
15.(1)见解析(2)函数的图象是轴对称图形,有条对称轴;(3)图象的两个分支成中心对称,对称中心是原点,两对对称点坐标为和、和.
解析:
(1)从正数,负数中各选几个值作为x的值,进而得到y的值,描点,连线即可;
(2)观察函数的图象即可确定其对称性;
(3)观察函数的图象得到中心对称图形,从而确定对称中心和两对对称点的坐标即可.
详解:
(1)列表得:
描点,连线得:
(2)函数的图象是轴对称图形,有条对称轴;(3)图象的两个分支成中心对称,对称中心是原点,两对对称点坐标为和、和.
点睛:
本题主要考查画反比例函数图像及反比例函数的对称性.
16.(1)图见解析;(2)与之间的函数关系式为,图像见解析;(3)W=,当日销售单价定为10元/个时,可获得最大日销售利润.
解析:
(1)根据已知描点即可;
(2)由表知xy=60,据此可得y (x>0),画出函数图象可得;
(3)根据总利润=每个贺卡的利润×贺卡的日销售数量可得函数解析式,根据反比例函数的性质求解可得.
详解:
(1)根据已知描点即可;
(2)由表可知,xy=60,∴y(x>0),函数图象如下:
(3)根据题意,得:
W=(x﹣2)?y=(x﹣2)?=60;
∵x≤10,∴12,则6048,即当x=10时,W取得最大值,最大值为48元.
答:当日销售单价x定为10元/个时,才能获得最大日销售利润,最大利润是48元.
点睛:
本题考查了反比例函数的应用,解题的关键是掌握反比例函数的性质、根据题意确定相等关系并据此列出函数解析式.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
26.2实际问题与反比例函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲、乙两地相距250千米,如果把汽车从甲地到乙地所用的时间y(小时),表示为汽车的平均速度为x(千米/小时)的函数,则此函数的图象大致是( ).
A. B.
C.D.
2.某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A.(x>0) B.(x≥0) C.y=300x(x≥0) D.y=300x(x>0)
3.一个圆柱的侧面展开图是一个面积为4平方单位的矩形,那么这个圆柱的母线长L和底面半径r之间的函数关系是
A.反比例函数 B.正比例函数 C.一次函数 D.二次函数
4.在公式ρ=中,当质量m一定时,密度与体积V之间的函数关系可用图象表示为( )
A. B. C.D.
5.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:
体积x(mL) 100 80 60 40 20
压强y(kPa) 60 75 100 150 300
则可以反映y与x之间的关系的式子是( )
A.y=3000x B.y=6000x C.y= D.y=
6.已知矩形的面积为,则如图给出的四个图象中,能大致呈现矩形相邻边长与之间的函数关系的是( )
A. B. C. D.
7.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.如果以此蓄电池为电源的用电器的限制电流不能超过6A,那么用电器的可变电阻R应控制在
A. B. C. D.
8.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V()的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将会爆炸,为了安全起见,气球的体积应( )
A.不小于 B.大于 C.不小于 D.小于
二、填空题
9.实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100 cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为___________,当S=2 cm2时, R=______________(Ω)
10.利用数学公式可建立反比例函数关系式,圆柱体的容积=_______×___.
11.三角形的面积是,它的底边(单位:)与这个底边上的高(单位:)的函数关系式为________.
12.已知△ABC的三个顶点为A(-1,1),B(-1,3),C(-3,-3),将△ABC向右平移m(m>0)个单位后,△ABC某一边的中点恰好落在反比例函数y= 的图象上,则m的值为________.
三、解答题
13.一个面积为42的长方形,其相邻两边长分别为x和y,请你写出与之间的函数解析式,并画出其图象.
14.“聚能”电厂现在有5000吨煤.
(1)求:这些煤能够使用的天数x(单位:天)与该厂平均每天用煤吨数y(单位:吨)之间的函数关系;
(2)若平均每天用煤200吨,则这批煤能用多少天?
(3)若该电厂前10天每天用煤200吨,后因各地用电紧张,每天用煤300吨,则这批煤共可用多少天?
15.(1)在所给平面直角坐标系中,画出反比例函数的图象;
(2)函数的图象是轴对称图形吗?有几条对称轴?
(3)上述图象的两个分支是否成中心对称,请指出对称中心,并写出两对对称点坐标.
16.某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价(元)与日销售量(个)之间有如下关系:
日销售单价(元) 3 4 5 6
日销售量(个) 20 15 12 10
(1)根据表中数据,在直角坐标系中描出实数对的对应点;
(2)猜测并确定与之间的函数关系式,并画出图像;
(3)设经营此贺卡的销售利润为元,求出与之间的函数关系式. 若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价定为多少时,才能获得最大日销售利润?
参考答案
1.D
解析:本题考查的是函数图象
根据路程、速度、时间三个量之间的关系即可得到结论.
由题意得,故选D.
2.A
解析:由“这批煤燃烧的天数=这批煤的总量÷每天烧煤的吨数”可得:
.
故选A.
3.A
解析:试题解析:根据题意,得2πrL=4,
则
所以这个圆柱的母线长L和底面半径r之间的函数关系是反比例函数.
故选A.
4.B
解析:∵在公式ρ=中,且质量m一定,
∴是v的反比例函数,且图象在第一象限.
故选B.
5.C
解析:
利用表格中数据得出函数关系,进而求出即可.
详解:
解:此函数是反比例函数,设解析式为:y=,则xy=k=6000,
故y与x之间的关系是y=.
故选C.
点睛:
此题主要考查了根据实际问题列反比例函数关系式.
6.A
解析:
根据矩形的面积公式得出xy=5,那么y与x之间的函数关系为反比例函数关系,再根据x、y所表示的实际意义得到x、y应大于0;即可得出答案.
详解:
∵矩形的面积为5,矩形相邻的两边长分别是y与x,
∴xy=5,
∴(x>0,y>0),
故选:A.
点睛:
考查反比例函数的应用,解答该类题目的关键是确定两个变量之间的函数关系,利用实际意义确定所在的象限.
7.C
解析:
根据题意首先求出反比例函数解析式,进而利用电器的限制不能超过12A,求出电器的可变电阻应控制的范围.
详解:
设反比例函数关系式为:I=,
把(2,3)代入得:k=2×3=6,
∴反比例函数关系式为:I=,
当I≤6时,则≤6,
R≥1,
故选:C.
点睛:
此题主要考查了反比例函数的应用,正确得出反比例函数解析式是解题关键.
8.C
解析:
由题意设设,把(1.6,60)代入得到k=96,推出,当P=120时,,由此即可判断.
详解:
因为气球内气体的气压p(kPa)是气体体积V()的反比例函数,所以可设,由题图可知,当时,,所以,所以.为了安全起见,气球内的气压应不大于120kPa,即,所以.
故选C.
点睛:
此题考查反比例函数的应用,解题关键在于把已知点代入解析式.
9.R= 14.5
解析:设反比例函数解析式为:R= ,
将(1,29)代入得:k=29,
则其函数关系式为:R= ,
当S=2cm2时,R==14.5(Ω).
故答案是:R=,14.5.
10. 底面积 高
【解析】圆柱的体积公式为:圆柱体的容积=底面积×高.
11.
解析:
根据等量关系“三角形的面积=底边底边上的高” 即可列出a与h的关系式.
详解:
解:由题意得a=220h=
故答案为:
点睛:
本题考查了反比例函数在实际生活中的应用,找出等量关系是解决此题的关键.
12.
解析:
根据中点的坐标和平移的规律,利用点在函数图像上,可解出m的值.
详解:
△ABC的三个顶点为A(-1,1),B(-1,3),C(-3,3)
∴AB的中点(-1,2),BC的中点(-2,0),AC的中点(-2,-1)
∴AB边的中点平移后为(-1+m,2),AC中点平移后为(-2+m,-1)
∵△ABC某一边中点落在反比例函数上
∴2(-1+m)=3或-1×(-2+m)=3
m=2.5或-1(舍去).
故答案是:.
点睛:
考查了反比例函数图象上点的坐标特点,关键是掌握反比例函数图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
13.y=,图象见解析.
解析:本题考查的是根据实际问题列函数关系式
根据长方形的面积公式可得其解析式,再用描点法画出其图象即可.
由题意得,函数解析式为,图象略.
14.(1)y=.(2)这批电煤能用25天.(3) 共可用20天.
解析:试题分析:(1)根据平均每天用煤吨数=总电煤 使用的天数列式;(2)当x=200代入反比例函数中计算即可;(3)先求出前10天剩余的电煤量,再除以300即可求出;
试题解析:
(1)y=.
(2)把x=200代入y=,
得y=25.
故这批电煤能用25天.
(3)前10天后还剩下5000-10×200=3000(吨)电煤,可以用=10(天),故共可用20天.
15.(1)见解析(2)函数的图象是轴对称图形,有条对称轴;(3)图象的两个分支成中心对称,对称中心是原点,两对对称点坐标为和、和.
解析:
(1)从正数,负数中各选几个值作为x的值,进而得到y的值,描点,连线即可;
(2)观察函数的图象即可确定其对称性;
(3)观察函数的图象得到中心对称图形,从而确定对称中心和两对对称点的坐标即可.
详解:
(1)列表得:
描点,连线得:
(2)函数的图象是轴对称图形,有条对称轴;(3)图象的两个分支成中心对称,对称中心是原点,两对对称点坐标为和、和.
点睛:
本题主要考查画反比例函数图像及反比例函数的对称性.
16.(1)图见解析;(2)与之间的函数关系式为,图像见解析;(3)W=,当日销售单价定为10元/个时,可获得最大日销售利润.
解析:
(1)根据已知描点即可;
(2)由表知xy=60,据此可得y (x>0),画出函数图象可得;
(3)根据总利润=每个贺卡的利润×贺卡的日销售数量可得函数解析式,根据反比例函数的性质求解可得.
详解:
(1)根据已知描点即可;
(2)由表可知,xy=60,∴y(x>0),函数图象如下:
(3)根据题意,得:
W=(x﹣2)?y=(x﹣2)?=60;
∵x≤10,∴12,则6048,即当x=10时,W取得最大值,最大值为48元.
答:当日销售单价x定为10元/个时,才能获得最大日销售利润,最大利润是48元.
点睛:
本题考查了反比例函数的应用,解题的关键是掌握反比例函数的性质、根据题意确定相等关系并据此列出函数解析式.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
