26.1反比例函数 同步练习(含详解)
图片预览

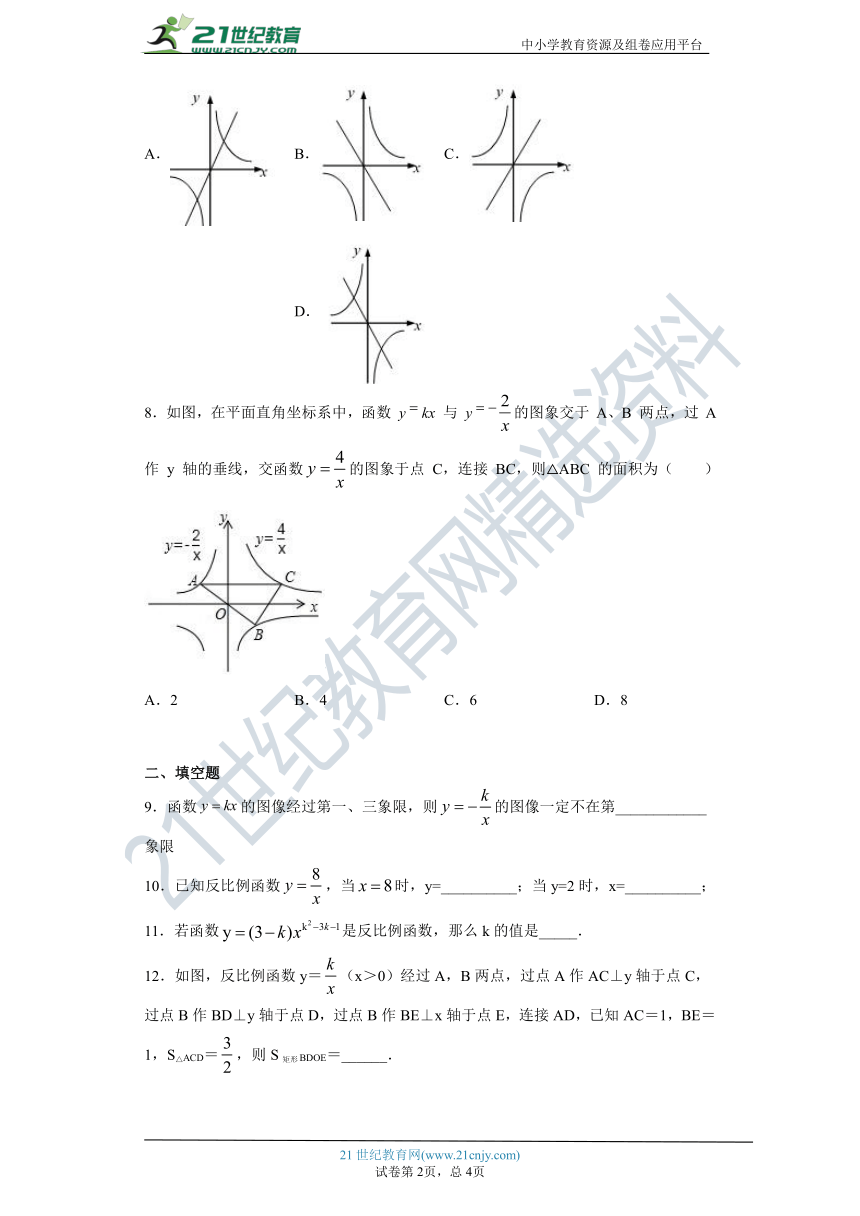



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
26.1反比例函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列函数中,哪个是反比例函数?( )
A. B. C. D.
2.在反比例函数图像的每一条曲线上,y都随x的增大而增大,则b的取值范围是( )
A.b=3 B. C. D.
3.一次函数y=ax-a与反比例函数y=(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
4.下列问题中,两个变量成反比例的是( )
A.商一定时(不为零),被除数与除数
B.等边三角形的面积与它的边长
C.长方形的长a不变时,长方形的周长C与它的宽b
D.货物的总价A一定时,货物的单价a与货物的数量x
5.下列函数中,随的增大而减少的函数是( )
A.=-2 B.= C.= D.=2x
6.下列问题中的两个变量成反比例关系的是( )
A.汽车以80千米/时的速度行驶s千米,用时t时
B.正方形的周长C与它的面积S
C.有一水池的容量为100立方米,每小时的灌水量q(立方米)与灌满水池所需要的时间t(小时)
D.圆的面积S与它的半径r
7.函数和(且)的图象大致是( )
A. B. C. D.
8.如图,在平面直角坐标系中,函数 y kx 与 y 的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数的图象于点 C,连接 BC,则△ABC 的面积为( )
A.2 B.4 C.6 D.8
二、填空题
9.函数的图像经过第一、三象限,则的图像一定不在第____________象限
10.已知反比例函数,当时,y=__________;当y=2时,x=__________;
11.若函数是反比例函数,那么k的值是_____.
12.如图,反比例函数y=(x>0)经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,S△ACD=,则S矩形BDOE=______.
三、解答题
13.已知反比例函数的图像经过直线上的点,求m和k的值
14.如图,一次函数y1=x+2的图象与反比例函数y2=(k≠0)的图象交于A、B两点,且点A的坐标为(1,m).
(1)求反比例函数的表达式及点B的坐标;
(2)根据图象直接写出当y1>y2时x的取值范围.
15.如图,正比例函数的图象与反比例函数的图象相交于A、B两点,其中点A的坐标为(3,4).
(1)分别写出这两个函数的表达式;
(2)你能求出点B的坐标吗?
16.如图,反比例函数的图象经过点A(,4),直线()与双曲线在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.
(1)求k 的值;
(2)当时,求△OCD 的面积;
(3)连接OQ,是否存在实数b,使得? 若存在,请求出b 的值;若不存在,请说明理由.
参考答案
1.B
解析:
由题意直接根据反比例函数的一般解析式是,对选项进行匹配即可.
详解:
解:反比例函数的解析式是,只有符合反比例函数的解析式的特征,其余的都不符合,
故选:B.
点睛:
本题考查反比例函数的概念,注意掌握反比例函数的一般解析式是是解题的关键.
2.C
解析:
由反比例函数的图象的每一条曲线上,y都随x的增大而增大,可得3-b<0,进而求出答案,作出选择.
详解:
解:∵反比例函数的图象的每一条曲线上,y都随x的增大而增大,
∴3-b<0,
∴b>3,
故选C.
点睛:
考查反比例函数的性质和一元一次不等式的解法,掌握反比例函数的性质是解决问题的关键.
3.D
解析:
详解:
解:A、由一次函数y=a(x-1)的图象y轴的正半轴相交可知-a>0,即a<0,与y=(x≠0)的图象a>0相矛盾,故A选项错误;
B、由一次函数y=a(x-1)的图象y轴的正半轴相交可知-a>0,即a<0,与y=(x≠0)的图象a>0相矛盾,故B选项错误;
C、由一次函数y=a(x-1)的图象与y轴的负半轴相交可知-a<0,即a>0,与y=(x≠0)的图象a<0相矛盾,故C选项错误;
D、由一次函数y=a(x-1)的图象可知a<0,与y=(x≠0)的图象a<0一致,故D选项正确.
故选D.
点睛:
本题考查反比例函数的图象;一次函数的图象.
4.D
解析:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.
详解:
A、商一定时(不为零),被除数和除数成正比例关系,故A错误;
B、等边三角形的面积与它的边长成二次函数关系;故B错误;
C、长方形的长a不变时,长方形的周长C与它的宽b成一次函数关系;故C错误;
D、货物的总价A一定时,货物的单价a与货物的数量x成反比例关系;故D正确.
点睛:
本题考查了反比例函数,正确区分正比例函数与反比例函数是解题关键.判断一个函数是否是反比例函数,首先看看两个变量是否具有反比例关系.
5.A
解析:
A.根据一次函数图象性质解题;
B.根据反比例函数图象解题;
C.根据一次函数图象性质解题;
D.根据正比例函数图象性质解题.
详解:
A.正比例函数y=-2x中,k<0,y随x增大而减小,故A正确;
B.在反比例函数y=中当k>0时,图象分布在一、三象限,在第一象限中,随的增大而减小,第三象限中,随的增大而减小,故选B错误;
C. 在反比例函数y=-中,图象分布在二、四象限,在第二象限中,随的增大而增大,在第四象限中,<0时随的增大而增大,故C错误;
D. 正比例函数y=2x中,k>0,y随x增大而增大,故D错误.
故选A.
点睛:
本题考查正比例函数图象的增减性、一次函数图象的增减性、反比例函数图象的增减性等知识,是重要考点,难度较易,掌握相关知识是解题关键.
6.C
解析:
根据题意逐一写出两个变量之间的函数关系,逐一分析即可得到答案.
详解:
解:A、汽车以80千米/时的速度行驶s千米,用时t时,则,是的正比例函数,故本选项错误;
B、正方形的面积是的二次函数,故本选项错误;
C、有一水池的容量为100立方米,每小时的灌水量q(立方米)与灌满水池所需要的时间t(小时)的函数关系为:,所以是的反比例函数,故本选项正确;
D、圆的面积S与它的半径r的函数关系为: 所以是的二次函数,故本选项错误.
故选:.
点睛:
本题考查的是列函数关系式,同时考查正比例函数,反比例函数,二次函数的含义,掌握反比例函数的含义是解题的关键.
7.B
解析:
根据反比例函数图象、正比例函数图象分析解答.
详解:
由条件可知,,
当时的图像经过第二、四象限,
当时的图像经过第一、三象限,故选B.
点睛:
本题考查反比例函数图象、正比例函数图象的特征,熟记图象与比例系数k的关系.
8.C
解析:
连接OC,根据图象先证明△AOC与△COB的面积相等,再根据题意分别计算出△AOD与△ODC的面积即可得△ABC的面积.
详解:
连接OC,设AC⊥y轴交y轴为点D,
如图,
∵反比例函数y=-为对称图形,
∴O为AB 的中点,
∴S△AOC=S△COB,
∵由题意得A点在y=-上,B点在y=上,
∴S△AOD=×OD×AD=xy=1;
S△COD=×OC×OD=xy=2;
S△AOC= S△AOD+ S△COD=3,
∴S△ABC= S△AOC+S△COB=6.
故答案选C.
点睛:
本题考查了一次函数与反比例函数的交点问题与三角形面积公式,解题的关键是熟练的掌握一次函数与反比例函数的交点问题与三角形面积运算.
9.一、三
解析:
因为正比例函数y=kx的图象经过第一、三象限,所以k>0,则-k<0,所以经过二、四象限,即可得解.
详解:
因为函数的图像经过第一、三象限,所以k>0,则-k<0,故的图像经过第二、四象限,那么的图像一定不在第一、三象限.
故答案为:一、三.
点睛:
本题考查正比例函数和反比例函数的图象性质,需注意判断x的系数的符号.
10.1 4
解析:
将代入反比例函数解析式,即可求y的值;将y=2代入反比例解析式,即可求x的值.
详解:
把代入的右边,解得,把y=2代入的左边,解得,
故答案为:1;4.
点睛:
本题考查反比例函数的性质、代数式求值等知识,是典型考点,难度容易,掌握相关知识是解题关键.
11.0
解析:
直接利用反比例函数的定义得出答案.
详解:
∵函数是反比例函数,
∴k2﹣3k﹣1=﹣1且3﹣k≠0,
解得:k1=0,k2=3,(不合题意舍去)
∴k=0.
故答案为:0.
点睛:
本题主要考查反比例函数的定义,掌握反比例函数的定义,是解题的关键.
12.4
解析:
根据三角形的面积求出CD,OC,进而确定点A的坐标,代入求出k的值,矩形BDOE的面积就是|k|,得出答案.
详解:
∵AC=1,S△ACD=,
∴CD=3,
∵ODBE是矩形,BE=1,
∴OD=1,OC=OD+CD=4,
∴A(1,4)代入反比例函数关系式得,k=4,
∴S矩形BDOE=|k|=4,
故答案为:4.
点睛:
本题考查了反比例函数的几何问题,掌握反比例函数的性质以及三角形的面积公式是解题的关键.
13.;.
解析:
先将P点坐标代入直线解析式可求出m值,进而可得P点坐标,再将P点坐标代入反比例函数解析式即可得k的值.
详解:
把,代入的左右两边解得;
把,代入的左右两边解得.
点睛:
本题主要考查了正比例函数和反比例函数的解析式,根据解析式求出点的坐标是解题的关键.
14.(1)y=,B(﹣3,﹣1);(2)﹣3<x<0或x>1
解析:
(1)把A点坐标代入一次函数解析式可求得m的值,可得到A点坐标,再把A点坐标代入反比例函数解析式可求得k的值,解析式联立,解方程即可求得B的坐标;
(2)根据图象观察直线在双曲线上方对应的x的范围即可求得.
详解:
解:(1)∵一次函数图象过A点,
∴m=1+2,解得m=3,
∴A点坐标为(1,3),
又∵反比例函数图象过A点,
∴k=1×3=3
∴反比例函数y=,
解方程组得:或,
∴B(﹣3,﹣1);
(2)当y1>y2时x的取值范围是﹣3<x<0或x>1.
点睛:
此题主要考查反比例函数与一次函数综合,解题的关键是熟知待定系数法的应用.
15.(1),(2)B(-3,-4)
解析:
(1)根据题意利用待定系数法把x=3,y=4分别代入,左右两边求解即可直接求得函数的解析式;
(2)由题意直接把,组成一个方程组,解得x=3,y=4或x=-3,y=-4即可求得B的坐标.
详解:
解:(1)把x=3,y=4分别代入,左右两边,得:4=3k1,,
解得,
所以解析式分别是,;
(2)把,组成一个方程组,
解得x=3,y=4或x=-3,y=-4,
则交点坐标是(3,4)、(-3,-4),
又A(3,4),
故B的坐标为:(-3,-4).
点睛:
本题考查待定系数法求函数的解析式,理解反比例函数图象的性质是解题的关键,注意(2)也可以利用反比例函数图象关于原点对称进行分析.
16.(1);(2)2;(3).
解析:试题分析:(1)把A(-1,4)代入双曲线的解析式即可;
(2)由,可得到直线CD的解析式为,从而得出CO=DO=2,即可得到的值;
(3)过Q作QE⊥y轴,垂足为E.然后分①b<0和②b>0两种情况讨论.当b<0时,由可知, OC=OD,∠OCD=∠ODC=45°,所以∠EDQ=∠DQE=45°,得到DE=EQ,由,可得到CO=QE,从而有Q(-b,2b),由点Q在双曲线的图象上,得到,即可得到b的值;②当b>0时,有,综和这两种情况,得到b的值.
试题解析:(1)∵A(-1,4)在双曲线上,∴;
(2)∵,∴直线CD的解析式为,∴C(-2,0),D(0,-2),∴CO=2,DO=2,∴=CO·DO=2;
(3)过Q作QE⊥y轴,垂足为E.
①当b<0时,由可知,C(b,0),D(0,b),∴OC=OD,∴∠OCD=∠ODC=45°,∴∠EDQ=∠DQE=45°,∴DE=EQ,∵,∴CO·DO=DO·QE,∴CO=QE,∴Q(-b,2b),∵点Q在双曲线的图象上,∴,∴,∴,∵b<0,∴;
②当b>0时,此时;
综上所述,当时,.
考点:反比例函数与一次函数的交点问题.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
26.1反比例函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列函数中,哪个是反比例函数?( )
A. B. C. D.
2.在反比例函数图像的每一条曲线上,y都随x的增大而增大,则b的取值范围是( )
A.b=3 B. C. D.
3.一次函数y=ax-a与反比例函数y=(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
4.下列问题中,两个变量成反比例的是( )
A.商一定时(不为零),被除数与除数
B.等边三角形的面积与它的边长
C.长方形的长a不变时,长方形的周长C与它的宽b
D.货物的总价A一定时,货物的单价a与货物的数量x
5.下列函数中,随的增大而减少的函数是( )
A.=-2 B.= C.= D.=2x
6.下列问题中的两个变量成反比例关系的是( )
A.汽车以80千米/时的速度行驶s千米,用时t时
B.正方形的周长C与它的面积S
C.有一水池的容量为100立方米,每小时的灌水量q(立方米)与灌满水池所需要的时间t(小时)
D.圆的面积S与它的半径r
7.函数和(且)的图象大致是( )
A. B. C. D.
8.如图,在平面直角坐标系中,函数 y kx 与 y 的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数的图象于点 C,连接 BC,则△ABC 的面积为( )
A.2 B.4 C.6 D.8
二、填空题
9.函数的图像经过第一、三象限,则的图像一定不在第____________象限
10.已知反比例函数,当时,y=__________;当y=2时,x=__________;
11.若函数是反比例函数,那么k的值是_____.
12.如图,反比例函数y=(x>0)经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,S△ACD=,则S矩形BDOE=______.
三、解答题
13.已知反比例函数的图像经过直线上的点,求m和k的值
14.如图,一次函数y1=x+2的图象与反比例函数y2=(k≠0)的图象交于A、B两点,且点A的坐标为(1,m).
(1)求反比例函数的表达式及点B的坐标;
(2)根据图象直接写出当y1>y2时x的取值范围.
15.如图,正比例函数的图象与反比例函数的图象相交于A、B两点,其中点A的坐标为(3,4).
(1)分别写出这两个函数的表达式;
(2)你能求出点B的坐标吗?
16.如图,反比例函数的图象经过点A(,4),直线()与双曲线在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.
(1)求k 的值;
(2)当时,求△OCD 的面积;
(3)连接OQ,是否存在实数b,使得? 若存在,请求出b 的值;若不存在,请说明理由.
参考答案
1.B
解析:
由题意直接根据反比例函数的一般解析式是,对选项进行匹配即可.
详解:
解:反比例函数的解析式是,只有符合反比例函数的解析式的特征,其余的都不符合,
故选:B.
点睛:
本题考查反比例函数的概念,注意掌握反比例函数的一般解析式是是解题的关键.
2.C
解析:
由反比例函数的图象的每一条曲线上,y都随x的增大而增大,可得3-b<0,进而求出答案,作出选择.
详解:
解:∵反比例函数的图象的每一条曲线上,y都随x的增大而增大,
∴3-b<0,
∴b>3,
故选C.
点睛:
考查反比例函数的性质和一元一次不等式的解法,掌握反比例函数的性质是解决问题的关键.
3.D
解析:
详解:
解:A、由一次函数y=a(x-1)的图象y轴的正半轴相交可知-a>0,即a<0,与y=(x≠0)的图象a>0相矛盾,故A选项错误;
B、由一次函数y=a(x-1)的图象y轴的正半轴相交可知-a>0,即a<0,与y=(x≠0)的图象a>0相矛盾,故B选项错误;
C、由一次函数y=a(x-1)的图象与y轴的负半轴相交可知-a<0,即a>0,与y=(x≠0)的图象a<0相矛盾,故C选项错误;
D、由一次函数y=a(x-1)的图象可知a<0,与y=(x≠0)的图象a<0一致,故D选项正确.
故选D.
点睛:
本题考查反比例函数的图象;一次函数的图象.
4.D
解析:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.
详解:
A、商一定时(不为零),被除数和除数成正比例关系,故A错误;
B、等边三角形的面积与它的边长成二次函数关系;故B错误;
C、长方形的长a不变时,长方形的周长C与它的宽b成一次函数关系;故C错误;
D、货物的总价A一定时,货物的单价a与货物的数量x成反比例关系;故D正确.
点睛:
本题考查了反比例函数,正确区分正比例函数与反比例函数是解题关键.判断一个函数是否是反比例函数,首先看看两个变量是否具有反比例关系.
5.A
解析:
A.根据一次函数图象性质解题;
B.根据反比例函数图象解题;
C.根据一次函数图象性质解题;
D.根据正比例函数图象性质解题.
详解:
A.正比例函数y=-2x中,k<0,y随x增大而减小,故A正确;
B.在反比例函数y=中当k>0时,图象分布在一、三象限,在第一象限中,随的增大而减小,第三象限中,随的增大而减小,故选B错误;
C. 在反比例函数y=-中,图象分布在二、四象限,在第二象限中,随的增大而增大,在第四象限中,<0时随的增大而增大,故C错误;
D. 正比例函数y=2x中,k>0,y随x增大而增大,故D错误.
故选A.
点睛:
本题考查正比例函数图象的增减性、一次函数图象的增减性、反比例函数图象的增减性等知识,是重要考点,难度较易,掌握相关知识是解题关键.
6.C
解析:
根据题意逐一写出两个变量之间的函数关系,逐一分析即可得到答案.
详解:
解:A、汽车以80千米/时的速度行驶s千米,用时t时,则,是的正比例函数,故本选项错误;
B、正方形的面积是的二次函数,故本选项错误;
C、有一水池的容量为100立方米,每小时的灌水量q(立方米)与灌满水池所需要的时间t(小时)的函数关系为:,所以是的反比例函数,故本选项正确;
D、圆的面积S与它的半径r的函数关系为: 所以是的二次函数,故本选项错误.
故选:.
点睛:
本题考查的是列函数关系式,同时考查正比例函数,反比例函数,二次函数的含义,掌握反比例函数的含义是解题的关键.
7.B
解析:
根据反比例函数图象、正比例函数图象分析解答.
详解:
由条件可知,,
当时的图像经过第二、四象限,
当时的图像经过第一、三象限,故选B.
点睛:
本题考查反比例函数图象、正比例函数图象的特征,熟记图象与比例系数k的关系.
8.C
解析:
连接OC,根据图象先证明△AOC与△COB的面积相等,再根据题意分别计算出△AOD与△ODC的面积即可得△ABC的面积.
详解:
连接OC,设AC⊥y轴交y轴为点D,
如图,
∵反比例函数y=-为对称图形,
∴O为AB 的中点,
∴S△AOC=S△COB,
∵由题意得A点在y=-上,B点在y=上,
∴S△AOD=×OD×AD=xy=1;
S△COD=×OC×OD=xy=2;
S△AOC= S△AOD+ S△COD=3,
∴S△ABC= S△AOC+S△COB=6.
故答案选C.
点睛:
本题考查了一次函数与反比例函数的交点问题与三角形面积公式,解题的关键是熟练的掌握一次函数与反比例函数的交点问题与三角形面积运算.
9.一、三
解析:
因为正比例函数y=kx的图象经过第一、三象限,所以k>0,则-k<0,所以经过二、四象限,即可得解.
详解:
因为函数的图像经过第一、三象限,所以k>0,则-k<0,故的图像经过第二、四象限,那么的图像一定不在第一、三象限.
故答案为:一、三.
点睛:
本题考查正比例函数和反比例函数的图象性质,需注意判断x的系数的符号.
10.1 4
解析:
将代入反比例函数解析式,即可求y的值;将y=2代入反比例解析式,即可求x的值.
详解:
把代入的右边,解得,把y=2代入的左边,解得,
故答案为:1;4.
点睛:
本题考查反比例函数的性质、代数式求值等知识,是典型考点,难度容易,掌握相关知识是解题关键.
11.0
解析:
直接利用反比例函数的定义得出答案.
详解:
∵函数是反比例函数,
∴k2﹣3k﹣1=﹣1且3﹣k≠0,
解得:k1=0,k2=3,(不合题意舍去)
∴k=0.
故答案为:0.
点睛:
本题主要考查反比例函数的定义,掌握反比例函数的定义,是解题的关键.
12.4
解析:
根据三角形的面积求出CD,OC,进而确定点A的坐标,代入求出k的值,矩形BDOE的面积就是|k|,得出答案.
详解:
∵AC=1,S△ACD=,
∴CD=3,
∵ODBE是矩形,BE=1,
∴OD=1,OC=OD+CD=4,
∴A(1,4)代入反比例函数关系式得,k=4,
∴S矩形BDOE=|k|=4,
故答案为:4.
点睛:
本题考查了反比例函数的几何问题,掌握反比例函数的性质以及三角形的面积公式是解题的关键.
13.;.
解析:
先将P点坐标代入直线解析式可求出m值,进而可得P点坐标,再将P点坐标代入反比例函数解析式即可得k的值.
详解:
把,代入的左右两边解得;
把,代入的左右两边解得.
点睛:
本题主要考查了正比例函数和反比例函数的解析式,根据解析式求出点的坐标是解题的关键.
14.(1)y=,B(﹣3,﹣1);(2)﹣3<x<0或x>1
解析:
(1)把A点坐标代入一次函数解析式可求得m的值,可得到A点坐标,再把A点坐标代入反比例函数解析式可求得k的值,解析式联立,解方程即可求得B的坐标;
(2)根据图象观察直线在双曲线上方对应的x的范围即可求得.
详解:
解:(1)∵一次函数图象过A点,
∴m=1+2,解得m=3,
∴A点坐标为(1,3),
又∵反比例函数图象过A点,
∴k=1×3=3
∴反比例函数y=,
解方程组得:或,
∴B(﹣3,﹣1);
(2)当y1>y2时x的取值范围是﹣3<x<0或x>1.
点睛:
此题主要考查反比例函数与一次函数综合,解题的关键是熟知待定系数法的应用.
15.(1),(2)B(-3,-4)
解析:
(1)根据题意利用待定系数法把x=3,y=4分别代入,左右两边求解即可直接求得函数的解析式;
(2)由题意直接把,组成一个方程组,解得x=3,y=4或x=-3,y=-4即可求得B的坐标.
详解:
解:(1)把x=3,y=4分别代入,左右两边,得:4=3k1,,
解得,
所以解析式分别是,;
(2)把,组成一个方程组,
解得x=3,y=4或x=-3,y=-4,
则交点坐标是(3,4)、(-3,-4),
又A(3,4),
故B的坐标为:(-3,-4).
点睛:
本题考查待定系数法求函数的解析式,理解反比例函数图象的性质是解题的关键,注意(2)也可以利用反比例函数图象关于原点对称进行分析.
16.(1);(2)2;(3).
解析:试题分析:(1)把A(-1,4)代入双曲线的解析式即可;
(2)由,可得到直线CD的解析式为,从而得出CO=DO=2,即可得到的值;
(3)过Q作QE⊥y轴,垂足为E.然后分①b<0和②b>0两种情况讨论.当b<0时,由可知, OC=OD,∠OCD=∠ODC=45°,所以∠EDQ=∠DQE=45°,得到DE=EQ,由,可得到CO=QE,从而有Q(-b,2b),由点Q在双曲线的图象上,得到,即可得到b的值;②当b>0时,有,综和这两种情况,得到b的值.
试题解析:(1)∵A(-1,4)在双曲线上,∴;
(2)∵,∴直线CD的解析式为,∴C(-2,0),D(0,-2),∴CO=2,DO=2,∴=CO·DO=2;
(3)过Q作QE⊥y轴,垂足为E.
①当b<0时,由可知,C(b,0),D(0,b),∴OC=OD,∴∠OCD=∠ODC=45°,∴∠EDQ=∠DQE=45°,∴DE=EQ,∵,∴CO·DO=DO·QE,∴CO=QE,∴Q(-b,2b),∵点Q在双曲线的图象上,∴,∴,∴,∵b<0,∴;
②当b>0时,此时;
综上所述,当时,.
考点:反比例函数与一次函数的交点问题.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
