28.1锐角三角函数 同步练习(含详解)
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
28.1锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为( )
A.( ,1) B.(1, ) C.( +1,1) D.(1,+1)
2.的值为( )
A. B.1 C. D.
3.△ABC中,∠C=90°,则的値是( )
A. B. C. D.
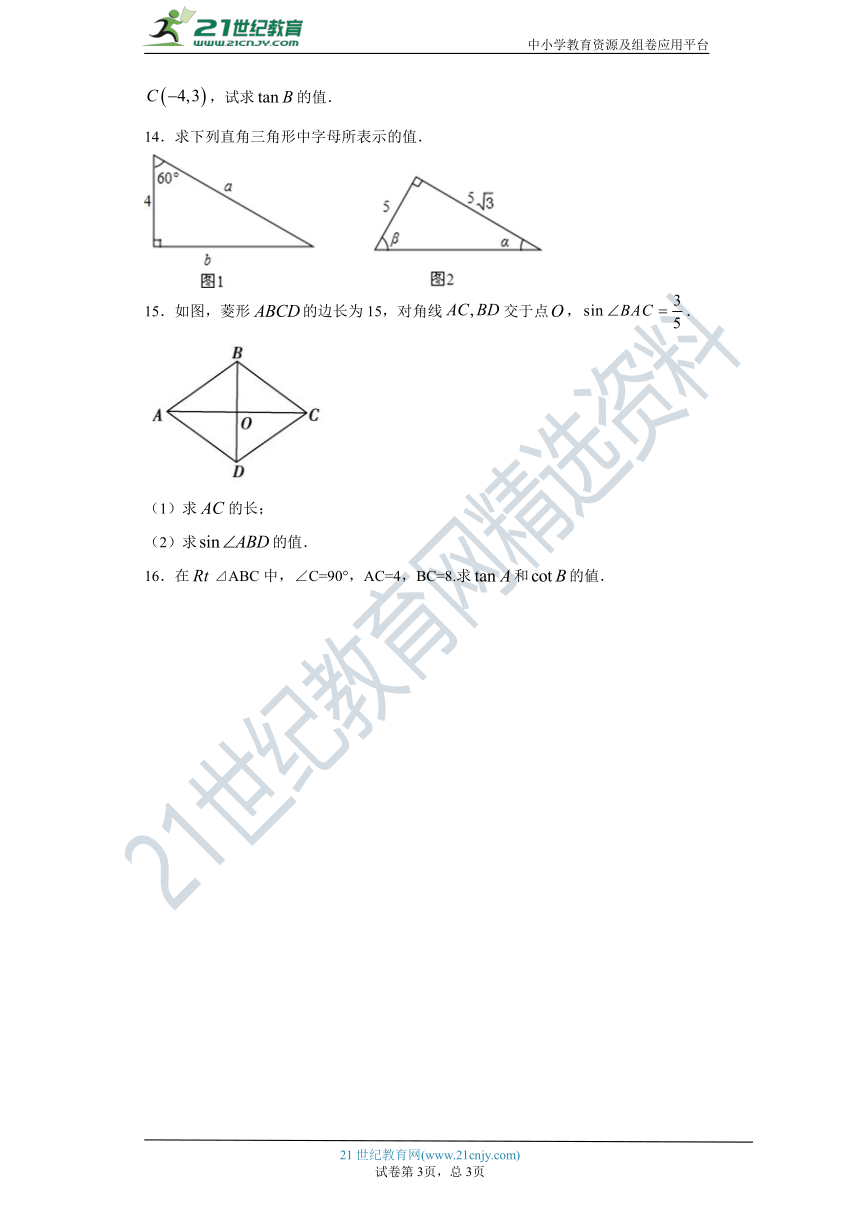
4.如果⊿ABC的各边长都扩大为原来的3倍,那么锐角A的正弦、余弦値是( )
A.都扩大为原来的3倍 B.都缩小为原来的
C.没有变化 D.不能确定
5.小明沿着与地面成30?的坡面向下走了2米,那么他下降(???)
A.1米 B.米 C.2米 D.米
6.如图,△ABC的顶点都是正方形网格中的格点,则sin∠ABC等于(???)
A. B. C. D.
7.如图,在中,,,,则的长为( )
A.2 B.4 C.6 D.8
8.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B.2 C. D.
二、填空题
9.如图,在Rt△ABC,∠C=90°,sinB=,AB=15,则AC的值是_____.
10.在⊿ABC中,∠B=90°,AB=5,BC=12,则______.
11.计算:______.
12.如图,在中,,,,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为__________cm.
三、解答题
13.在直角坐标系中,的三个顶点的坐标分 别为、、,试求的值.
14.求下列直角三角形中字母所表示的值.
15.如图,菱形的边长为15,对角线交于点,.
(1)求的长;
(2)求的值.
16.在⊿ABC中,∠C=90°,AC=4,BC=8.求和的値.
参考答案
1.C
解析:试题解析:过点作 轴于点,
∵是菱形,
∴点的坐标为:
故选C.
2.B
解析:
根据特殊角的正切值即可得.
详解:
,
故选:B.
点睛:
本题考查了特殊角的正切值,熟记特殊角的正切值是解题关键.
3.A
解析:
根据锐角三角函数的定义求解即可.
详解:
解:,
故选:A.
点睛:
本题考查锐角三角函数的定义,掌握锐角三角函数的定义是解题的关键.
4.C
解析:
根据相似三角形的判定定理、正弦、余弦的概念解答.
详解:
三角形各边长度都扩大为原来的3倍,
∴得到的三角形与原三角形相似,
∴锐角A的大小不变,
∴锐角A的正弦、余弦值不变,
故选:C.
点睛:
三角形的形状没有改变,边的比值没有发生变化.
5.A
解析:
直接利用坡度的定义,坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,可画出三角形,结合图形运用三角函数求解即可.
详解:
如图所示:
∵AB=2,∠C=90°,∠A=30°.
∴他下降的高度BC=ABsin30°=1(米).
故选A
点睛:
此题主要考查了坡度的定义和特殊角的三角函数值,正确记忆特殊角的三角函数值是解题的关键.
6.C
解析:试题解析:设正方形网格每个小正方形边长为1,则BC边上的高为2,则 , .
故本题应选C.
7.C
解析:
本题利用正弦三角函数的定义即可直接作答.
详解:
∵,,,
∴,
∴.
故选:C.
点睛:
本题考查三角函数,解题关键在于按照定义找准对应边,其次注意计算仔细即可.
8.C
解析:试题分析:连结CD,可得CD为直径,在Rt△OCD中,CD=6,OC=2,根据勾股定理求得OD=4
所以tan∠CDO=,由圆周角定理得,∠OBC=∠CDO,则tan∠OBC=,故答案选C.
考点:圆周角定理;锐角三角函数的定义.
9.12
解析:
由sinB=得AC=ABsinB,据此可得.
详解:
解:在Rt△ABC中,∵sinB=,
∴AC=ABsinB=15×=12,
故答案为:12.
点睛:
此题主要考查三角函数的应用,解题的关键是熟知正弦函数的定义.
10.
解析:
根据余弦的定义进行解答
详解:
在Rt△ABC中,AC=,
,故填.
点睛:
本题考查三角函数的定义,余弦值=角的邻边与斜边之比.
11.
解析:
先计算特殊角的三角函数值,再计算含乘方的有理数混合运算即可得.
详解:
,
故答案为:.
点睛:
本题考查了特殊角的三角函数值、含乘方的有理数混合运算,熟记特殊角的三角函数值是解题关键.
12.5
解析:
连接、、过作于,求出、值,求出、值,求出、值,代入求出即可.
详解:
解:连接、、过作于,
在中,,,,
,,
,
的垂直平分线,
同理,
,
同理,
,
故答案是:5.
点睛:
本题考查了线段垂直平分线性质,等腰三角形的性质,含30度角的直角三角形性质,解直角三角形等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力.
13.
解析:
根据题意,在坐标系中找到三点位置,利用关系求解即可.
详解:
如图,AC=2,BC=3,
tanB==.
点睛:
本题考查作图能力及角的正切值,找到三点的位置是关键.
14.(1),;(2),
解析:
(1) 根据特殊角60三角函数关系便可求出a,b
(2) 根据边的关系,边可以找到正切值,从而找到
详解:
(1)cos60
a=
tan60
b=4
(2)tan=
点睛:
抓特殊角的三角函数关系,这样便可以顺利找到答案了.
15.(1);(2).
解析:
(1)根据菱形的性质得出,得到Rt△AOB,再由正弦函数求出BO的长度,由勾股定理求出AO长度,从而计算出AC的长度即可;
(2)在中,根据正弦函数的定义即可求出.
详解:
解:(1)∵四边形是菱形,
∴.
∵,
∴,
∴,
∴.
(2)在中,,,
∴.
点睛:
本题考查了正弦函数的定义及计算问题,解题的关键是掌握正弦函数的定义.
16.2;2
解析:
根据锐角的正切等于对边比邻边,余切等于邻边比对边即可解答.
详解:
解:∵⊿ABC中,∠C=90°,AC=4,BC=8.
∴,.
即=2,=2.
点睛:
本题考了锐角三角函数的定义,熟练掌握在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,余切为邻边比对边是解题关键.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
28.1锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=,则点B的坐标为( )
A.( ,1) B.(1, ) C.( +1,1) D.(1,+1)
2.的值为( )
A. B.1 C. D.
3.△ABC中,∠C=90°,则的値是( )
A. B. C. D.
4.如果⊿ABC的各边长都扩大为原来的3倍,那么锐角A的正弦、余弦値是( )
A.都扩大为原来的3倍 B.都缩小为原来的
C.没有变化 D.不能确定
5.小明沿着与地面成30?的坡面向下走了2米,那么他下降(???)
A.1米 B.米 C.2米 D.米
6.如图,△ABC的顶点都是正方形网格中的格点,则sin∠ABC等于(???)
A. B. C. D.
7.如图,在中,,,,则的长为( )
A.2 B.4 C.6 D.8
8.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B.2 C. D.
二、填空题
9.如图,在Rt△ABC,∠C=90°,sinB=,AB=15,则AC的值是_____.
10.在⊿ABC中,∠B=90°,AB=5,BC=12,则______.
11.计算:______.
12.如图,在中,,,,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为__________cm.
三、解答题
13.在直角坐标系中,的三个顶点的坐标分 别为、、,试求的值.
14.求下列直角三角形中字母所表示的值.
15.如图,菱形的边长为15,对角线交于点,.
(1)求的长;
(2)求的值.
16.在⊿ABC中,∠C=90°,AC=4,BC=8.求和的値.
参考答案
1.C
解析:试题解析:过点作 轴于点,
∵是菱形,
∴点的坐标为:
故选C.
2.B
解析:
根据特殊角的正切值即可得.
详解:
,
故选:B.
点睛:
本题考查了特殊角的正切值,熟记特殊角的正切值是解题关键.
3.A
解析:
根据锐角三角函数的定义求解即可.
详解:
解:,
故选:A.
点睛:
本题考查锐角三角函数的定义,掌握锐角三角函数的定义是解题的关键.
4.C
解析:
根据相似三角形的判定定理、正弦、余弦的概念解答.
详解:
三角形各边长度都扩大为原来的3倍,
∴得到的三角形与原三角形相似,
∴锐角A的大小不变,
∴锐角A的正弦、余弦值不变,
故选:C.
点睛:
三角形的形状没有改变,边的比值没有发生变化.
5.A
解析:
直接利用坡度的定义,坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,可画出三角形,结合图形运用三角函数求解即可.
详解:
如图所示:
∵AB=2,∠C=90°,∠A=30°.
∴他下降的高度BC=ABsin30°=1(米).
故选A
点睛:
此题主要考查了坡度的定义和特殊角的三角函数值,正确记忆特殊角的三角函数值是解题的关键.
6.C
解析:试题解析:设正方形网格每个小正方形边长为1,则BC边上的高为2,则 , .
故本题应选C.
7.C
解析:
本题利用正弦三角函数的定义即可直接作答.
详解:
∵,,,
∴,
∴.
故选:C.
点睛:
本题考查三角函数,解题关键在于按照定义找准对应边,其次注意计算仔细即可.
8.C
解析:试题分析:连结CD,可得CD为直径,在Rt△OCD中,CD=6,OC=2,根据勾股定理求得OD=4
所以tan∠CDO=,由圆周角定理得,∠OBC=∠CDO,则tan∠OBC=,故答案选C.
考点:圆周角定理;锐角三角函数的定义.
9.12
解析:
由sinB=得AC=ABsinB,据此可得.
详解:
解:在Rt△ABC中,∵sinB=,
∴AC=ABsinB=15×=12,
故答案为:12.
点睛:
此题主要考查三角函数的应用,解题的关键是熟知正弦函数的定义.
10.
解析:
根据余弦的定义进行解答
详解:
在Rt△ABC中,AC=,
,故填.
点睛:
本题考查三角函数的定义,余弦值=角的邻边与斜边之比.
11.
解析:
先计算特殊角的三角函数值,再计算含乘方的有理数混合运算即可得.
详解:
,
故答案为:.
点睛:
本题考查了特殊角的三角函数值、含乘方的有理数混合运算,熟记特殊角的三角函数值是解题关键.
12.5
解析:
连接、、过作于,求出、值,求出、值,求出、值,代入求出即可.
详解:
解:连接、、过作于,
在中,,,,
,,
,
的垂直平分线,
同理,
,
同理,
,
故答案是:5.
点睛:
本题考查了线段垂直平分线性质,等腰三角形的性质,含30度角的直角三角形性质,解直角三角形等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力.
13.
解析:
根据题意,在坐标系中找到三点位置,利用关系求解即可.
详解:
如图,AC=2,BC=3,
tanB==.
点睛:
本题考查作图能力及角的正切值,找到三点的位置是关键.
14.(1),;(2),
解析:
(1) 根据特殊角60三角函数关系便可求出a,b
(2) 根据边的关系,边可以找到正切值,从而找到
详解:
(1)cos60
a=
tan60
b=4
(2)tan=
点睛:
抓特殊角的三角函数关系,这样便可以顺利找到答案了.
15.(1);(2).
解析:
(1)根据菱形的性质得出,得到Rt△AOB,再由正弦函数求出BO的长度,由勾股定理求出AO长度,从而计算出AC的长度即可;
(2)在中,根据正弦函数的定义即可求出.
详解:
解:(1)∵四边形是菱形,
∴.
∵,
∴,
∴,
∴.
(2)在中,,,
∴.
点睛:
本题考查了正弦函数的定义及计算问题,解题的关键是掌握正弦函数的定义.
16.2;2
解析:
根据锐角的正切等于对边比邻边,余切等于邻边比对边即可解答.
详解:
解:∵⊿ABC中,∠C=90°,AC=4,BC=8.
∴,.
即=2,=2.
点睛:
本题考了锐角三角函数的定义,熟练掌握在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,余切为邻边比对边是解题关键.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
