29.3课题学习制作立体模型 同步练习(含详解)
文档属性
| 名称 | 29.3课题学习制作立体模型 同步练习(含详解) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 12:02:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
29.3课题学习制作立体模型
学校:___________姓名:___________班级:___________考号:___________
一、单选题
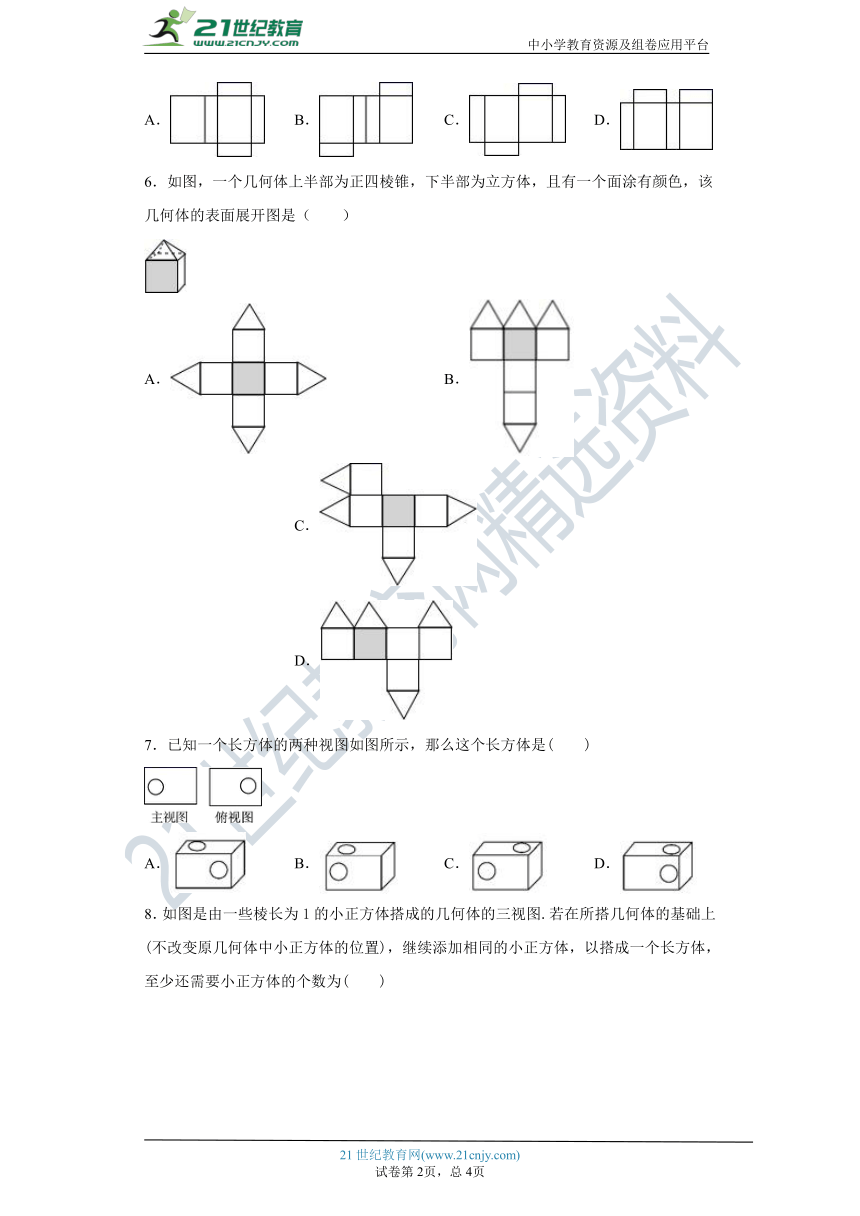
1.一个几何体的三视图如图所示,则这个几何体是( )
A.球体 B.圆锥 C.棱柱 D.圆柱
2.一个几何体的三视图如图所示,则这个几何体是( )
A.三棱锥 B.三棱柱 C.圆柱 D.长方体
3.由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.9
4.如图,贤贤同学用手工纸制作一个台灯灯罩,做好后发现上口太小了,于是他把纸灯罩对齐压扁,剪去上面一截后,正好合适,以下裁剪示意图中,正确的是( )
A. B. C. D.
5.如图是一个长方体包装盒,则它的平面展开图是
A. B. C. D.
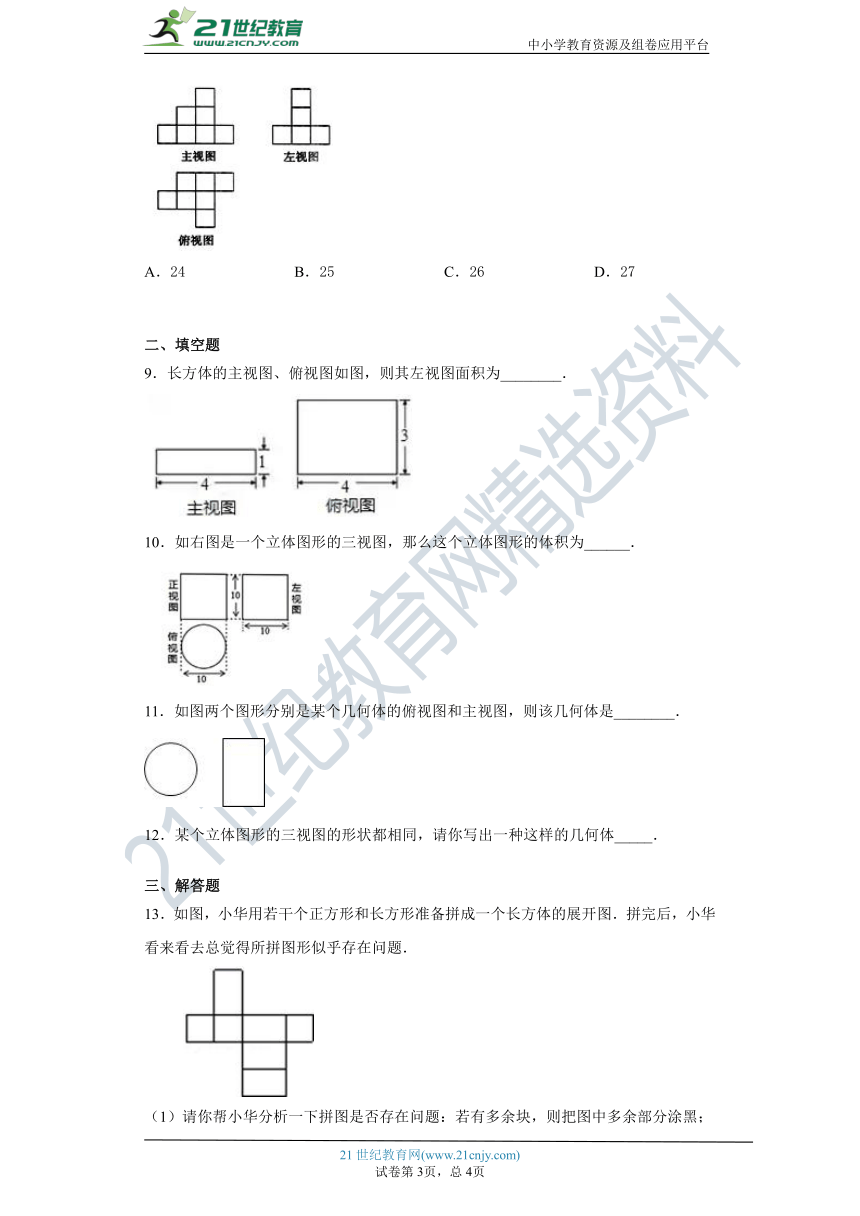
6.如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( )
A. B. C. D.
7.已知一个长方体的两种视图如图所示,那么这个长方体是( )
A. B. C. D.
8.如图是由一些棱长为1的小正方体搭成的几何体的三视图.若在所搭几何体的基础上(不改变原几何体中小正方体的位置),继续添加相同的小正方体,以搭成一个长方体,至少还需要小正方体的个数为( )
A.24 B.25 C.26 D.27
二、填空题
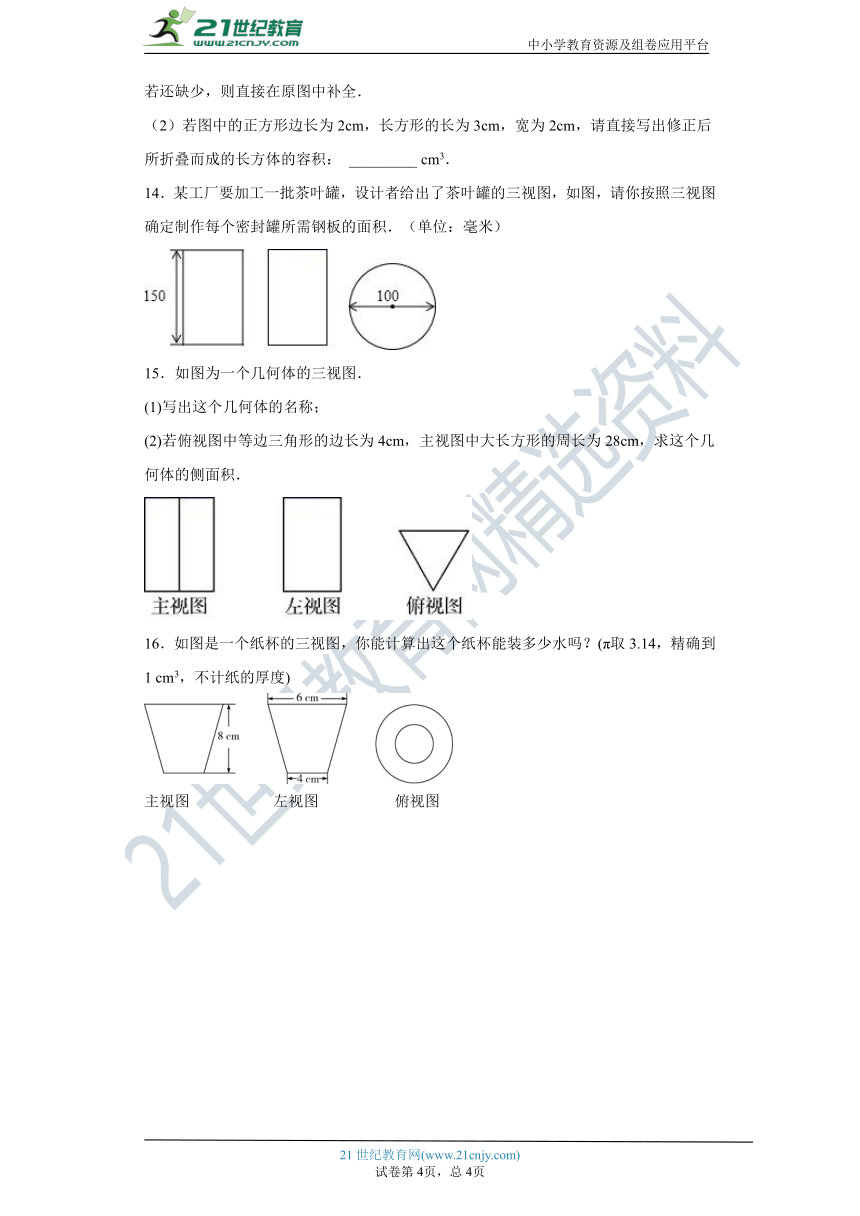
9.长方体的主视图、俯视图如图,则其左视图面积为________.
10.如右图是一个立体图形的三视图,那么这个立体图形的体积为______.
11.如图两个图形分别是某个几何体的俯视图和主视图,则该几何体是________.
12.某个立体图形的三视图的形状都相同,请你写出一种这样的几何体_____.
三、解答题
13.如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全.
(2)若图中的正方形边长为2cm,长方形的长为3cm,宽为2cm,请直接写出修正后所折叠而成的长方体的容积: _________ cm3.
14.某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个密封罐所需钢板的面积.(单位:毫米)
15.如图为一个几何体的三视图.
(1)写出这个几何体的名称;
(2)若俯视图中等边三角形的边长为4cm,主视图中大长方形的周长为28cm,求这个几何体的侧面积.
16.如图是一个纸杯的三视图,你能计算出这个纸杯能装多少水吗?(π取3.14,精确到1 cm3,不计纸的厚度)
主视图 左视图 俯视图
参考答案
1.D
解析:试题分析:观察可知,这个几何体的俯视图为圆,主视图与左视图都是矩形,所以这个几何体是圆柱,故答案选D.
考点:几何体的三视图.
2.B
解析:
根据三视图的知识,正视图为两个矩形,左视图为一个矩形,俯视图为一个三角形,故这个几何体为直三棱柱.
详解:
解:根据图中三视图的形状,符合条件的只有直三棱柱,因此这个几何体的名称是直三棱柱.
故选B.
3.A
解析:试题分析:综合三视图,我们可得出,这个几何体的底层应该有3个小正方体,第二层应该有1个小正方体,因此搭成这个几何体的小正方体的个数为3+1=4个,故选A.
考点:由三视图判断几何体.
4.A
解析:
详解:
压扁后圆台的形状如图A,
故选A.
5.A
解析:试题分析:由四棱柱四个侧面和上下两个底面的特征可知,A、可以拼成一个长方体,B、C、D、不符合长方体的展开图的特征,故不是长方体的展开图.故选A.
考点:几何体的展开图.
6.B
解析:
由平面图形的折叠及几何体的展开图解题,注意带图案的一个面不是底面.
详解:
解:选项A和C带图案的一个面是底面,不能折叠成原几何体的形式;
选项B能折叠成原几何体的形式;
选项D折叠后下面带三角形的面与原几何体中的位置不同.
故选:B.
点睛:
本题主要考查了几何体的展开图解题时勿忘记正四棱柱的特征及正方体展开图的各种情形注意做题时可亲自动手操作一下,增强空间想象能力.
7.C
解析:
由主视图可知正面有一个圆孔靠近左边,上面有一个圆孔靠近右边,即可判断
详解:
由主视图可知,这个长方体的正面有一个圆孔,而且圆孔靠近左边;由俯视图可知长方体的上面有一个圆孔,且靠近右边.由此便可得出正确答案.
点睛:
此题考查三视图,难度不大
8.C
解析:
首先根据该几何体的三视图确定需要的小立方块的块数分布情况,然后确定搭成一个大长方体需要的块数.
详解:
解:由俯视图易得最底层有7个小立方体,第二层有2个小立方体,第三层有1小立方体,其小正方块分布情况如下:
那么共有7+2+1=10个几何体组成.若搭成一个大长方体,共需3×4×3=36个小立方体,所以还需36-10=26个小立方体.
故选:C.
点睛:
本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
9.3
解析:
详解:
解:根据三视图可得长方体的长为4、宽为3、高为1,则左视图的面积=宽×高=3.
故答案为:3
点睛:
本题考查利用三视图求面积.
10.250π
解析:
根据三视图可得这个几何体是一个底面直径为10,高为10的圆柱,再根据圆柱的体积公式列式计算即可.
详解:
解:根据这个立体图形的三视图可得:这个几何体是一个圆柱,底面直径为10,高为10,
则这个立体图形的体积为:π×52×10=250π,
故答案为:250π.
点睛:
本题考查了由三视图判断几何体,考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
11.圆柱
解析:
根据圆柱体的三视图分别为圆、矩形、矩形,即可得出答案.
详解:
主视图是矩形,俯视图是圆,符合这样条件的几何体是圆柱.
故答案为圆柱.
点睛:
本题考查了利用三视图判断几何体.熟记常见几何体的三视图是解题的关键.
12.正方体(或球体)(答案不唯一)
解析:试题分析:根据立体图形的三视图的形状都相同进行判断,即可得出答案.
解:正方体的三视图都是正方形,球体的三视图都是圆.
故答案为正方体(或球体).
13.(1)作图见解析和;(2)12.
解析:(1)由于长方体有六个面,且相对的两个面全等,所以展开图是6个长方形(包括正方形),而图中所拼图共有7个面,所以有多余块,应该去掉一个;又所拼图中有3个全等的正方形,结合平面图形的折叠可知,可将第二行最左边的一个正方形去掉;
(2)由题意可知,此长方体的长、宽、高可分别看作3厘米、2厘米和2厘米,将数据代入长方体的体积公式即可求解.
解:(1)拼图存在问题,如图:
(2)折叠而成的长方体的容积为;3×2×2=12(cm3).
故答案为12.
14..
解析:试题分析:从三视图可以得出,主视图以及侧视图都是一个矩形,俯视图为一个圆形,则可得出该几何体是一个圆柱.
试题解析:由三视图可知茶叶罐的形状为圆柱体,并且茶叶罐的底面直径2R为100毫米,高H为150毫米,∵每个密封罐所需钢板的面积即为该圆柱体的表面积,
∴S表面积===(毫米2),故制作每个密封罐所需钢板的面积为毫米2.
考点:1.由三视图判断几何体;2.圆柱的计算.
15.(1)这个几何体是三棱柱;(2)120 cm2
解析:试题分析:(1)根据三视图的知识,主视图以及左视图都是长方形,俯视图为三角形,即可求出俯视图的面积;
(2)先求出大长方形的长为28÷2-4=10cm,再根据侧面积为3个长方形,它的长和宽分别为10cm,4cm,即可求出几何体的表面积.
解:(1)这个几何体是三棱柱;
(2)28÷2-4
=14-4
=10(cm),
10×4×3=120(cm2).
故这个几何体的侧面积是120 cm2.
点睛:本题主要考查由三视图确定几何体和求几何体的面积等相关知识,考查学生的空间想象能力.注意:棱柱的侧面都是长方形,上下底面是几边形就是几棱柱.
16.159cm3
解析:
由三视图可知,这个纸杯的容积类似一个圆台,上面直径为6cm,下面直径为4cm,高为8cm,根据圆台体积公式:V=π(R2+Rr+r2)h,列式计算即可求解.
详解:
由题意推知几何体类似一个圆台,上面直径为6cm,下面直径为4cm,高为8cm,
所以其体积为:×3.14×[(6÷2)2+(6÷2)×(4÷2)+(4÷2)2]×8
=×3.14×(9+6+4)×8
=×3.14×19×8
≈159(cm3).
故这个纸杯大约能装159cm3水.
点睛:
本题考查三视图、圆台的体积,考查简单几何体的三视图的运用.培养同学们的空间想象能力和基本的运算能力.基础题.
_21?????????è?????(www.21cnjy.com)_
试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
29.3课题学习制作立体模型
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个几何体的三视图如图所示,则这个几何体是( )
A.球体 B.圆锥 C.棱柱 D.圆柱
2.一个几何体的三视图如图所示,则这个几何体是( )
A.三棱锥 B.三棱柱 C.圆柱 D.长方体
3.由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.9
4.如图,贤贤同学用手工纸制作一个台灯灯罩,做好后发现上口太小了,于是他把纸灯罩对齐压扁,剪去上面一截后,正好合适,以下裁剪示意图中,正确的是( )
A. B. C. D.
5.如图是一个长方体包装盒,则它的平面展开图是
A. B. C. D.
6.如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( )
A. B. C. D.
7.已知一个长方体的两种视图如图所示,那么这个长方体是( )
A. B. C. D.
8.如图是由一些棱长为1的小正方体搭成的几何体的三视图.若在所搭几何体的基础上(不改变原几何体中小正方体的位置),继续添加相同的小正方体,以搭成一个长方体,至少还需要小正方体的个数为( )
A.24 B.25 C.26 D.27
二、填空题
9.长方体的主视图、俯视图如图,则其左视图面积为________.
10.如右图是一个立体图形的三视图,那么这个立体图形的体积为______.
11.如图两个图形分别是某个几何体的俯视图和主视图,则该几何体是________.
12.某个立体图形的三视图的形状都相同,请你写出一种这样的几何体_____.
三、解答题
13.如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全.
(2)若图中的正方形边长为2cm,长方形的长为3cm,宽为2cm,请直接写出修正后所折叠而成的长方体的容积: _________ cm3.
14.某工厂要加工一批茶叶罐,设计者给出了茶叶罐的三视图,如图,请你按照三视图确定制作每个密封罐所需钢板的面积.(单位:毫米)
15.如图为一个几何体的三视图.
(1)写出这个几何体的名称;
(2)若俯视图中等边三角形的边长为4cm,主视图中大长方形的周长为28cm,求这个几何体的侧面积.
16.如图是一个纸杯的三视图,你能计算出这个纸杯能装多少水吗?(π取3.14,精确到1 cm3,不计纸的厚度)
主视图 左视图 俯视图
参考答案
1.D
解析:试题分析:观察可知,这个几何体的俯视图为圆,主视图与左视图都是矩形,所以这个几何体是圆柱,故答案选D.
考点:几何体的三视图.
2.B
解析:
根据三视图的知识,正视图为两个矩形,左视图为一个矩形,俯视图为一个三角形,故这个几何体为直三棱柱.
详解:
解:根据图中三视图的形状,符合条件的只有直三棱柱,因此这个几何体的名称是直三棱柱.
故选B.
3.A
解析:试题分析:综合三视图,我们可得出,这个几何体的底层应该有3个小正方体,第二层应该有1个小正方体,因此搭成这个几何体的小正方体的个数为3+1=4个,故选A.
考点:由三视图判断几何体.
4.A
解析:
详解:
压扁后圆台的形状如图A,
故选A.
5.A
解析:试题分析:由四棱柱四个侧面和上下两个底面的特征可知,A、可以拼成一个长方体,B、C、D、不符合长方体的展开图的特征,故不是长方体的展开图.故选A.
考点:几何体的展开图.
6.B
解析:
由平面图形的折叠及几何体的展开图解题,注意带图案的一个面不是底面.
详解:
解:选项A和C带图案的一个面是底面,不能折叠成原几何体的形式;
选项B能折叠成原几何体的形式;
选项D折叠后下面带三角形的面与原几何体中的位置不同.
故选:B.
点睛:
本题主要考查了几何体的展开图解题时勿忘记正四棱柱的特征及正方体展开图的各种情形注意做题时可亲自动手操作一下,增强空间想象能力.
7.C
解析:
由主视图可知正面有一个圆孔靠近左边,上面有一个圆孔靠近右边,即可判断
详解:
由主视图可知,这个长方体的正面有一个圆孔,而且圆孔靠近左边;由俯视图可知长方体的上面有一个圆孔,且靠近右边.由此便可得出正确答案.
点睛:
此题考查三视图,难度不大
8.C
解析:
首先根据该几何体的三视图确定需要的小立方块的块数分布情况,然后确定搭成一个大长方体需要的块数.
详解:
解:由俯视图易得最底层有7个小立方体,第二层有2个小立方体,第三层有1小立方体,其小正方块分布情况如下:
那么共有7+2+1=10个几何体组成.若搭成一个大长方体,共需3×4×3=36个小立方体,所以还需36-10=26个小立方体.
故选:C.
点睛:
本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
9.3
解析:
详解:
解:根据三视图可得长方体的长为4、宽为3、高为1,则左视图的面积=宽×高=3.
故答案为:3
点睛:
本题考查利用三视图求面积.
10.250π
解析:
根据三视图可得这个几何体是一个底面直径为10,高为10的圆柱,再根据圆柱的体积公式列式计算即可.
详解:
解:根据这个立体图形的三视图可得:这个几何体是一个圆柱,底面直径为10,高为10,
则这个立体图形的体积为:π×52×10=250π,
故答案为:250π.
点睛:
本题考查了由三视图判断几何体,考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
11.圆柱
解析:
根据圆柱体的三视图分别为圆、矩形、矩形,即可得出答案.
详解:
主视图是矩形,俯视图是圆,符合这样条件的几何体是圆柱.
故答案为圆柱.
点睛:
本题考查了利用三视图判断几何体.熟记常见几何体的三视图是解题的关键.
12.正方体(或球体)(答案不唯一)
解析:试题分析:根据立体图形的三视图的形状都相同进行判断,即可得出答案.
解:正方体的三视图都是正方形,球体的三视图都是圆.
故答案为正方体(或球体).
13.(1)作图见解析和;(2)12.
解析:(1)由于长方体有六个面,且相对的两个面全等,所以展开图是6个长方形(包括正方形),而图中所拼图共有7个面,所以有多余块,应该去掉一个;又所拼图中有3个全等的正方形,结合平面图形的折叠可知,可将第二行最左边的一个正方形去掉;
(2)由题意可知,此长方体的长、宽、高可分别看作3厘米、2厘米和2厘米,将数据代入长方体的体积公式即可求解.
解:(1)拼图存在问题,如图:
(2)折叠而成的长方体的容积为;3×2×2=12(cm3).
故答案为12.
14..
解析:试题分析:从三视图可以得出,主视图以及侧视图都是一个矩形,俯视图为一个圆形,则可得出该几何体是一个圆柱.
试题解析:由三视图可知茶叶罐的形状为圆柱体,并且茶叶罐的底面直径2R为100毫米,高H为150毫米,∵每个密封罐所需钢板的面积即为该圆柱体的表面积,
∴S表面积===(毫米2),故制作每个密封罐所需钢板的面积为毫米2.
考点:1.由三视图判断几何体;2.圆柱的计算.
15.(1)这个几何体是三棱柱;(2)120 cm2
解析:试题分析:(1)根据三视图的知识,主视图以及左视图都是长方形,俯视图为三角形,即可求出俯视图的面积;
(2)先求出大长方形的长为28÷2-4=10cm,再根据侧面积为3个长方形,它的长和宽分别为10cm,4cm,即可求出几何体的表面积.
解:(1)这个几何体是三棱柱;
(2)28÷2-4
=14-4
=10(cm),
10×4×3=120(cm2).
故这个几何体的侧面积是120 cm2.
点睛:本题主要考查由三视图确定几何体和求几何体的面积等相关知识,考查学生的空间想象能力.注意:棱柱的侧面都是长方形,上下底面是几边形就是几棱柱.
16.159cm3
解析:
由三视图可知,这个纸杯的容积类似一个圆台,上面直径为6cm,下面直径为4cm,高为8cm,根据圆台体积公式:V=π(R2+Rr+r2)h,列式计算即可求解.
详解:
由题意推知几何体类似一个圆台,上面直径为6cm,下面直径为4cm,高为8cm,
所以其体积为:×3.14×[(6÷2)2+(6÷2)×(4÷2)+(4÷2)2]×8
=×3.14×(9+6+4)×8
=×3.14×19×8
≈159(cm3).
故这个纸杯大约能装159cm3水.
点睛:
本题考查三视图、圆台的体积,考查简单几何体的三视图的运用.培养同学们的空间想象能力和基本的运算能力.基础题.
_21?????????è?????(www.21cnjy.com)_
试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
