29.2三视图 同步练习(含详解)
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
29.2三视图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
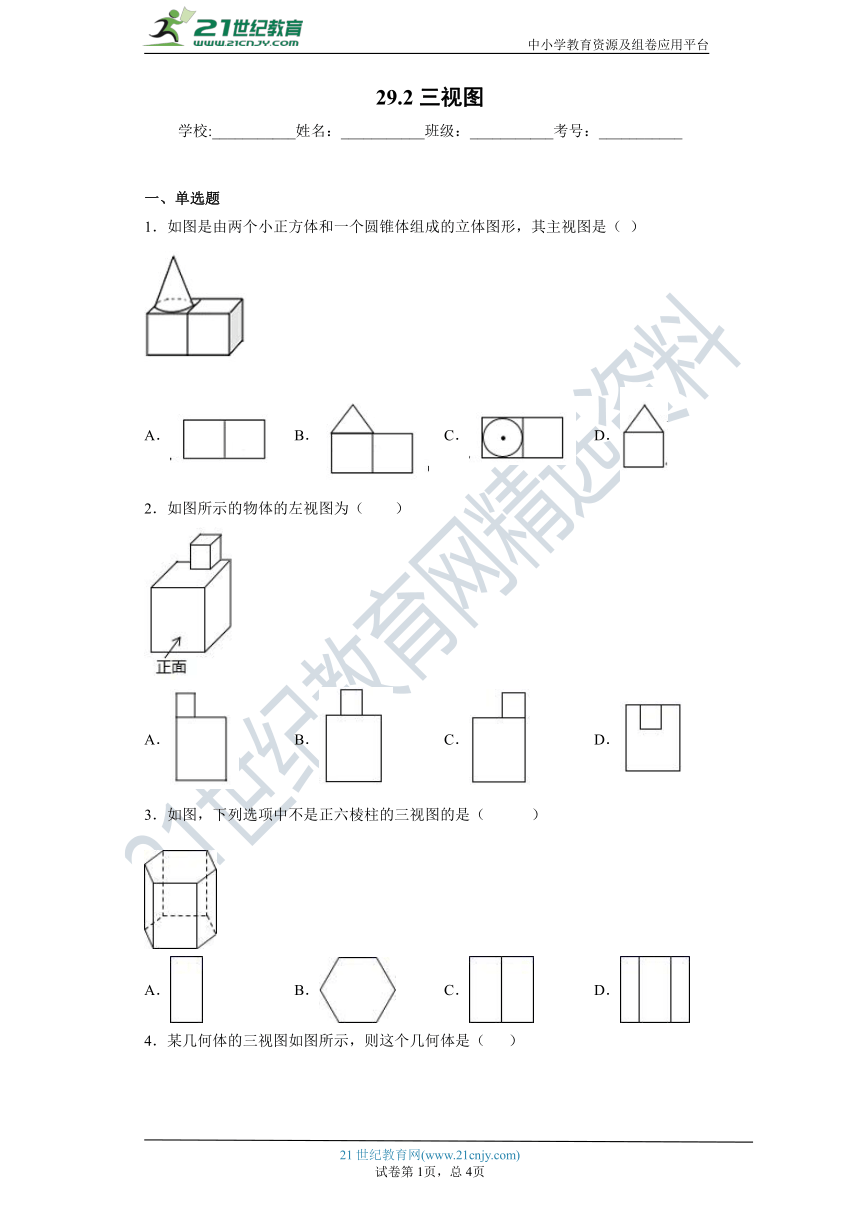
1.如图是由两个小正方体和一个圆锥体组成的立体图形,其主视图是( )
A. B. C. D.
2.如图所示的物体的左视图为( )
A. B. C. D.
3.如图,下列选项中不是正六棱柱的三视图的是( )
A. B. C. D.
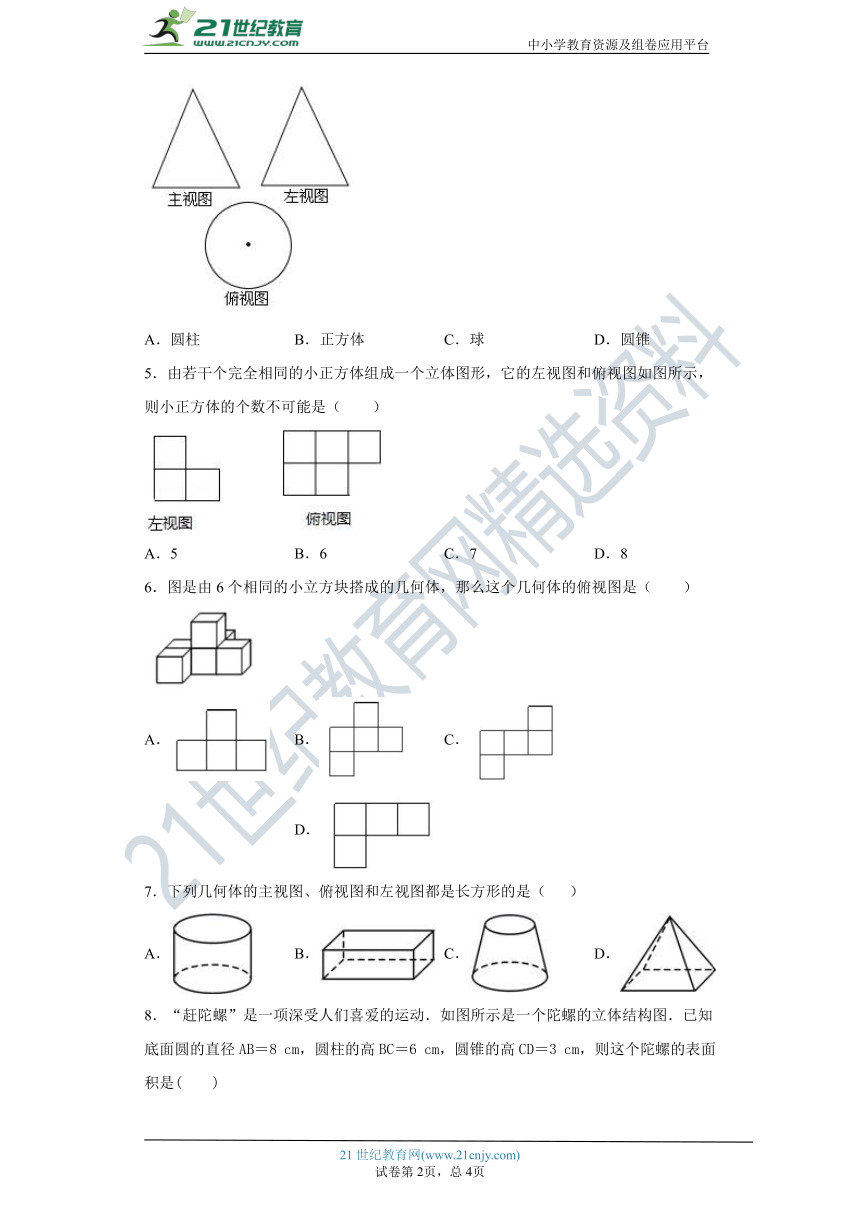
4.某几何体的三视图如图所示,则这个几何体是( )
A.圆柱 B.正方体 C.球 D.圆锥
5.由若干个完全相同的小正方体组成一个立体图形,它的左视图和俯视图如图所示,则小正方体的个数不可能是( )
A.5 B.6 C.7 D.8
6.图是由6个相同的小立方块搭成的几何体,那么这个几何体的俯视图是( )
A. B. C. D.
7.下列几何体的主视图、俯视图和左视图都是长方形的是( )
A. B. C. D.
8.“赶陀螺”是一项深受人们喜爱的运动.如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8 cm,圆柱的高BC=6 cm,圆锥的高CD=3 cm,则这个陀螺的表面积是( )
A.68π cm2 B.74π cm2 C.84π cm2 D.100π cm2
二、填空题
9.一个由大小相同的正方体构成的几何体的三视图如图,这个几何体是由___________个正方体组成的.
10.工人师傅要制造某一工件,他想知道工件的高,需要看到三视图中的___或___.
11.由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是_____个.
12.如图,这是一个长方体的主视图和俯视图,由图示数据(单元:cm)可以得出该长方体的体积是______cm3.
三、解答题
13.如图是几个正方体所组成的几何体的俯视图,小正方形中的数字表示该位置小正方块的个数.请画出这个几何体的主视图和左视图.
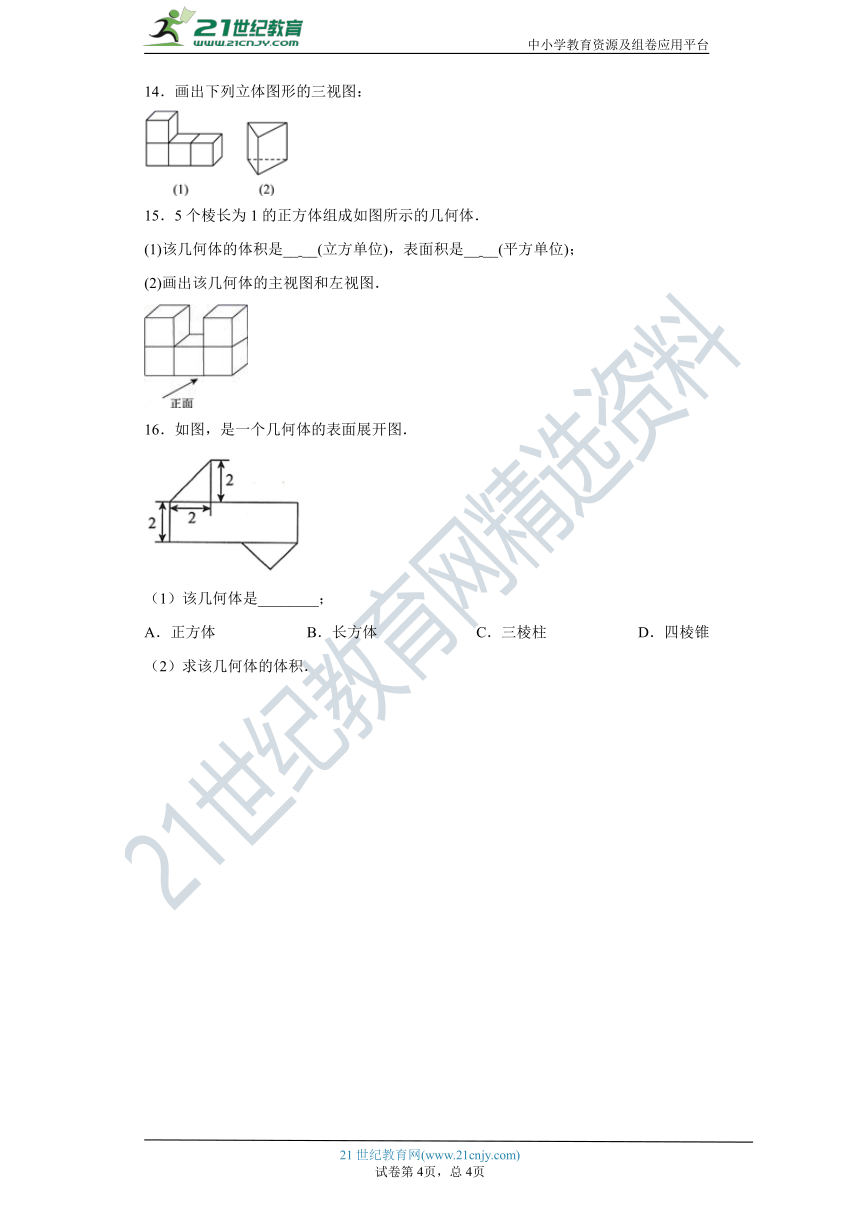
14.画出下列立体图形的三视图:
15.5个棱长为1的正方体组成如图所示的几何体.
(1)该几何体的体积是__ __(立方单位),表面积是__ __(平方单位);
(2)画出该几何体的主视图和左视图.
16.如图,是一个几何体的表面展开图.
(1)该几何体是________;
A.正方体 B.长方体 C.三棱柱 D.四棱锥
(2)求该几何体的体积.
参考答案
1.B
解析:主视图是从正面看得到的视图,从正面看上面圆锥看见的是:三角形,下面两个正方体看见的是两个正方形.故选B.
2.A
解析:试题分析:先观察原立体图形和俯视图中两个正方体的位置关系,从几何体的左边看去是2个正方体叠在一起,并且它们左边对齐,所以左视图是A
故选A
考点:左视图
3.A
解析:
主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
详解:
正六棱柱三视图分别为:三个左右相邻的矩形,两个左右相邻的矩形,正六边形.
故选A.
点睛:
本题考查了几何体的三种视图,注意所有的看到的棱都应表现在三视图中.
4.D
解析:
由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
详解:
解:根据主视图和左视图为三角形判断出是锥体,根据俯视图是圆形和圆心可判断出这个几何体应该是圆锥,
故选:D.
点睛:
本题考查由三视图判断几何体.
5.A
解析:分析】直接利用左视图以及俯视图进而分析得出答案.
详解:由左视图可得,第2层上至少一个小立方体,
第1层一共有5个小立方体,故小正方体的个数最少为:6个,故小正方体的个数不可能是5个.
故选A.
点睛:此题主要考查了由三视图判断几何体,正确想象出最少时几何体的形状是解题关键.
6.B
解析:
根据三视图的定义,可得:俯视图是在水平面内从上向下观察几何体得到的平面图形,逐一判断选项,即可得到答案.
详解:
在水平面内从上向下观察几何体,得到的图形有三行,第一行在第二列处有一个正方形,第二行有三个正方形,第三行在第一列处有一个正方形.
故选B.
点睛:
本题主要考查三视图描述几何体,掌握三视图的定义,是解题的关键.
7.B
解析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.找到几何体的三视图即可作出判断:
A、主视图和左视图为矩形,俯视图为圆,故选项错误;
B、主视图为矩形,俯视图和左视图都为矩形,故选项正确;
C、主视图和左视图为等腰梯形,俯视图为圆环,故选项错误;
D、主视图和左视图为三角形,俯视图为有对角线的矩形,故选项错误.
故选B.
8.C
解析:试题分析:∵底面圆的直径为8cm,高为3cm,∴母线长为5cm,∴其表面积=π×4×5+42π+8π×6=84πcm2,故选C.
考点:圆锥的计算;几何体的表面积.
9.4
解析:
从主视图可以看出每一层小正方体的层数和个数,从俯视图中可以看出最底层小正方体的个数及形状,从而算出总的个数
详解:
综合三视图,我们可得出,这个几何体的底层应该有3个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体的小正方体的个数为3+1=4个,
故答案为4.
点睛:
本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
10.主视图 左视图
解析:
从正面看某一工件,看到的是工件的长和高,从左面看到的是工件的宽和高,从上面看到的是工件的长和宽,由此问题得解.
详解:
解:要想知道工件的高,需从正面或左面看,因此需要看到三视图中的主视图或左视图.
故答案为:主视图,左视图.
点睛:
本题考查了三视图,解答此类问题,需要注意从三个方向看物体,所看的是到物体的哪些部分.
11.7
解析:
根据几何体的三视图可进行求解.
详解:
解:根据题意得:
则搭成该几何体的小正方体最多是1+1+1+2+2=7(个).
故答案为7.
点睛:
本题主要考查几何体的三视图,熟练掌握几何体的三视图是解题的关键.
12.24
解析:
根据主视图和俯视图求出长方体的长宽高即可解题.
详解:
解:由主视图可知长方体长为4,高为3,由俯视图可知长方体宽为2,
∴长方体体积==24 cm3
点睛:
本题考查了利用三视图求立体图形的体积,属于简单题,看懂三视图是解题关键.
13.作图见解析.
解析:试题分析:首先画出主视图:(1)按照自左到右的顺序,在俯视图的最下方依次标上1、2、3三个序号,注意,顺序不能乱;(2)三个序号就意味着几何体的主视图是有三列构成,因此,按照自左到右的顺序先画出有三个小正方形构成的长方形;(3)数出每列中小正方形的最大个数,这样,我们就知道,这几何体的主视图应该是3、2、4型;(4)在对应的小正方形的上面依次画出最大数目个小正方形,得到主视图.同理画出左视图.
试题解析:
点睛:主视图与左视图的高度是相等的;主视图与俯视图的长度是相等的左视图与俯视图的宽是相等的.
14.见解析.
解析:
根据从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图,画出三视图即可.
详解:
解:如图所示:
(1)
(2)
点睛:
考查了作图?三视图,主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;注意所有看到的棱及顶点都应表现在三视图中.
15.(1)5;22;(2)作图见解析.
解析:(1)几何体的体积为5个正方体的体积和,表面积为22个正方形的面积;
(2)主视图从左往右看3列正方形的个数依次为2,1,2;左视图1列正方形的个数为2.
解:(1)每个正方体的体积为1,∴组合几何体的体积为5×1=5;
∵组合几何体的前面和后面共有5×2=10个正方形,上下共有6个正方形,左右共6个正方形,每个正方形的面积为1,
∴组合几何体的表面积为22.
故答案为5,22;
(2)作图如下:
16.(1)C;(2)4
解析:
(1)本题根据展开图可直接得出答案.
(2)本题根据体积等于底面积乘高求解即可.
详解:
(1)本题可根据展开图中两个全等的等腰直角三角形,以此判定该几何体为三棱柱,故选C.
(2)由图已知:该几何体底面积为等腰三角形面积;该几何体的高为2;
故该几何体体积底面积高.
点睛:
本题考查几何体展开图以及体积求法,根据展开图推测几何体时需要以展开图的特征位置作为推测依据,求解体积或者面积时按照公式求解即可.
_21?????????è?????(www.21cnjy.com)_
试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
29.2三视图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图是由两个小正方体和一个圆锥体组成的立体图形,其主视图是( )
A. B. C. D.
2.如图所示的物体的左视图为( )
A. B. C. D.
3.如图,下列选项中不是正六棱柱的三视图的是( )
A. B. C. D.
4.某几何体的三视图如图所示,则这个几何体是( )
A.圆柱 B.正方体 C.球 D.圆锥
5.由若干个完全相同的小正方体组成一个立体图形,它的左视图和俯视图如图所示,则小正方体的个数不可能是( )
A.5 B.6 C.7 D.8
6.图是由6个相同的小立方块搭成的几何体,那么这个几何体的俯视图是( )
A. B. C. D.
7.下列几何体的主视图、俯视图和左视图都是长方形的是( )
A. B. C. D.
8.“赶陀螺”是一项深受人们喜爱的运动.如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8 cm,圆柱的高BC=6 cm,圆锥的高CD=3 cm,则这个陀螺的表面积是( )
A.68π cm2 B.74π cm2 C.84π cm2 D.100π cm2
二、填空题
9.一个由大小相同的正方体构成的几何体的三视图如图,这个几何体是由___________个正方体组成的.
10.工人师傅要制造某一工件,他想知道工件的高,需要看到三视图中的___或___.
11.由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是_____个.
12.如图,这是一个长方体的主视图和俯视图,由图示数据(单元:cm)可以得出该长方体的体积是______cm3.
三、解答题
13.如图是几个正方体所组成的几何体的俯视图,小正方形中的数字表示该位置小正方块的个数.请画出这个几何体的主视图和左视图.
14.画出下列立体图形的三视图:
15.5个棱长为1的正方体组成如图所示的几何体.
(1)该几何体的体积是__ __(立方单位),表面积是__ __(平方单位);
(2)画出该几何体的主视图和左视图.
16.如图,是一个几何体的表面展开图.
(1)该几何体是________;
A.正方体 B.长方体 C.三棱柱 D.四棱锥
(2)求该几何体的体积.
参考答案
1.B
解析:主视图是从正面看得到的视图,从正面看上面圆锥看见的是:三角形,下面两个正方体看见的是两个正方形.故选B.
2.A
解析:试题分析:先观察原立体图形和俯视图中两个正方体的位置关系,从几何体的左边看去是2个正方体叠在一起,并且它们左边对齐,所以左视图是A
故选A
考点:左视图
3.A
解析:
主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
详解:
正六棱柱三视图分别为:三个左右相邻的矩形,两个左右相邻的矩形,正六边形.
故选A.
点睛:
本题考查了几何体的三种视图,注意所有的看到的棱都应表现在三视图中.
4.D
解析:
由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
详解:
解:根据主视图和左视图为三角形判断出是锥体,根据俯视图是圆形和圆心可判断出这个几何体应该是圆锥,
故选:D.
点睛:
本题考查由三视图判断几何体.
5.A
解析:分析】直接利用左视图以及俯视图进而分析得出答案.
详解:由左视图可得,第2层上至少一个小立方体,
第1层一共有5个小立方体,故小正方体的个数最少为:6个,故小正方体的个数不可能是5个.
故选A.
点睛:此题主要考查了由三视图判断几何体,正确想象出最少时几何体的形状是解题关键.
6.B
解析:
根据三视图的定义,可得:俯视图是在水平面内从上向下观察几何体得到的平面图形,逐一判断选项,即可得到答案.
详解:
在水平面内从上向下观察几何体,得到的图形有三行,第一行在第二列处有一个正方形,第二行有三个正方形,第三行在第一列处有一个正方形.
故选B.
点睛:
本题主要考查三视图描述几何体,掌握三视图的定义,是解题的关键.
7.B
解析:主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.找到几何体的三视图即可作出判断:
A、主视图和左视图为矩形,俯视图为圆,故选项错误;
B、主视图为矩形,俯视图和左视图都为矩形,故选项正确;
C、主视图和左视图为等腰梯形,俯视图为圆环,故选项错误;
D、主视图和左视图为三角形,俯视图为有对角线的矩形,故选项错误.
故选B.
8.C
解析:试题分析:∵底面圆的直径为8cm,高为3cm,∴母线长为5cm,∴其表面积=π×4×5+42π+8π×6=84πcm2,故选C.
考点:圆锥的计算;几何体的表面积.
9.4
解析:
从主视图可以看出每一层小正方体的层数和个数,从俯视图中可以看出最底层小正方体的个数及形状,从而算出总的个数
详解:
综合三视图,我们可得出,这个几何体的底层应该有3个小正方体,第二层应该有1个小正方体,
因此搭成这个几何体的小正方体的个数为3+1=4个,
故答案为4.
点睛:
本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.
10.主视图 左视图
解析:
从正面看某一工件,看到的是工件的长和高,从左面看到的是工件的宽和高,从上面看到的是工件的长和宽,由此问题得解.
详解:
解:要想知道工件的高,需从正面或左面看,因此需要看到三视图中的主视图或左视图.
故答案为:主视图,左视图.
点睛:
本题考查了三视图,解答此类问题,需要注意从三个方向看物体,所看的是到物体的哪些部分.
11.7
解析:
根据几何体的三视图可进行求解.
详解:
解:根据题意得:
则搭成该几何体的小正方体最多是1+1+1+2+2=7(个).
故答案为7.
点睛:
本题主要考查几何体的三视图,熟练掌握几何体的三视图是解题的关键.
12.24
解析:
根据主视图和俯视图求出长方体的长宽高即可解题.
详解:
解:由主视图可知长方体长为4,高为3,由俯视图可知长方体宽为2,
∴长方体体积==24 cm3
点睛:
本题考查了利用三视图求立体图形的体积,属于简单题,看懂三视图是解题关键.
13.作图见解析.
解析:试题分析:首先画出主视图:(1)按照自左到右的顺序,在俯视图的最下方依次标上1、2、3三个序号,注意,顺序不能乱;(2)三个序号就意味着几何体的主视图是有三列构成,因此,按照自左到右的顺序先画出有三个小正方形构成的长方形;(3)数出每列中小正方形的最大个数,这样,我们就知道,这几何体的主视图应该是3、2、4型;(4)在对应的小正方形的上面依次画出最大数目个小正方形,得到主视图.同理画出左视图.
试题解析:
点睛:主视图与左视图的高度是相等的;主视图与俯视图的长度是相等的左视图与俯视图的宽是相等的.
14.见解析.
解析:
根据从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图,画出三视图即可.
详解:
解:如图所示:
(1)
(2)
点睛:
考查了作图?三视图,主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;注意所有看到的棱及顶点都应表现在三视图中.
15.(1)5;22;(2)作图见解析.
解析:(1)几何体的体积为5个正方体的体积和,表面积为22个正方形的面积;
(2)主视图从左往右看3列正方形的个数依次为2,1,2;左视图1列正方形的个数为2.
解:(1)每个正方体的体积为1,∴组合几何体的体积为5×1=5;
∵组合几何体的前面和后面共有5×2=10个正方形,上下共有6个正方形,左右共6个正方形,每个正方形的面积为1,
∴组合几何体的表面积为22.
故答案为5,22;
(2)作图如下:
16.(1)C;(2)4
解析:
(1)本题根据展开图可直接得出答案.
(2)本题根据体积等于底面积乘高求解即可.
详解:
(1)本题可根据展开图中两个全等的等腰直角三角形,以此判定该几何体为三棱柱,故选C.
(2)由图已知:该几何体底面积为等腰三角形面积;该几何体的高为2;
故该几何体体积底面积高.
点睛:
本题考查几何体展开图以及体积求法,根据展开图推测几何体时需要以展开图的特征位置作为推测依据,求解体积或者面积时按照公式求解即可.
_21?????????è?????(www.21cnjy.com)_
试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
