19.1.2函数的图象 同步练习(含详解)
文档属性
| 名称 | 19.1.2函数的图象 同步练习(含详解) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 15:13:22 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
19.1.2函数的图象
学校:___________姓名:___________班级:___________考号:___________
一、单选题
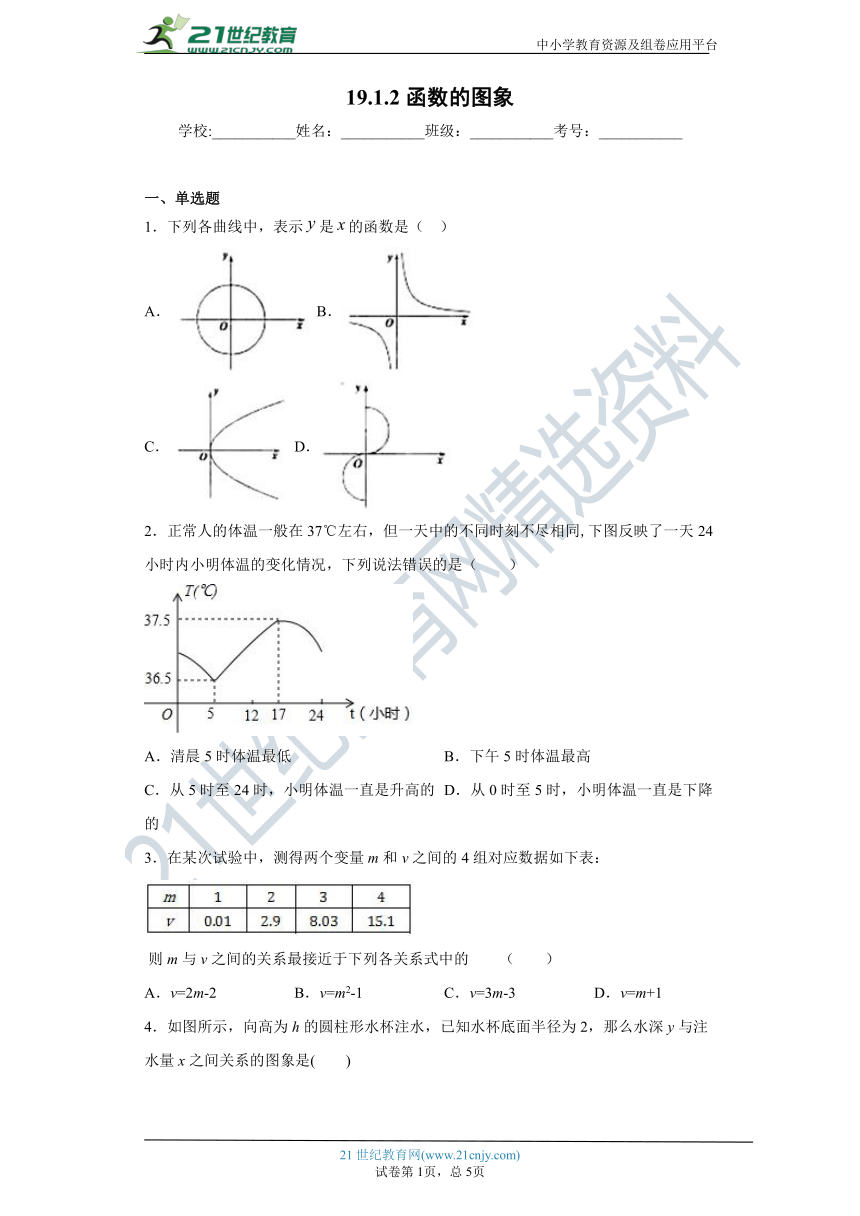
1.下列各曲线中,表示是的函数是( )
A.B.
C. D.
2.正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同,下图反映了一天24小时内小明体温的变化情况,下列说法错误的是( )
A.清晨5时体温最低 B.下午5时体温最高
C.从5时至24时,小明体温一直是升高的 D.从0时至5时,小明体温一直是下降的
3.在某次试验中,测得两个变量m和v之间的4组对应数据如下表:
?则m与v之间的关系最接近于下列各关系式中的 ( )
A.v=2m-2 B.v=m2-1 C.v=3m-3 D.v=m+1
4.如图所示,向高为h的圆柱形水杯注水,已知水杯底面半径为2,那么水深y与注水量x之间关系的图象是( )
A.(A) B.(B) C.(C) D.(D)
5.一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为( )
A.y=10x+30 B.y=40x C.y=10+30x D.y=20x
6.某学习小组做了一个实验:从一幢100 m高的楼顶随手放下一只苹果,测得有关数据如下:
下落时间t(s) 1 2 3 4
下落高度h(m) 5 20 45 80
则下列说法错误的是( )
A.苹果每秒下落的路程越来越长 B.苹果每秒下落的路程不变
C.苹果下落的速度越来越快 D.可以推测,苹果落到地面的时间不超过5秒
7.如图,是一台自动测温仪记录的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
A.凌晨4时气温最低为-3℃
B.14时气温最高为8℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
8.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()
A. B. C. D.
二、填空题
9.在中,∠C=90°,AC=6,BC=8,设P是BC上任一点,P点与B、C不重合,且,若,则与之间的函数关系式是_____,自变量取值范围为_____.
10.在地球表面的一定高度内,每升高1千米,温度下降.已知地面温度为,设高度为h千米时的温度是t,则t与h之间的关系是________________
11.小明从家跑步到学校,接着马上原路步行回家.如图所示为小明离家的路程与时间的图像,则小明回家的速度是每分钟步行________m.
12.已知函数y=,下列关于它的图象与性质,正确的是____.(写出所有正确的序号)
①函数图象与坐标轴无交点; ②函数图象关于y轴对称;
③y随x的增大而减小; ④函数有最大值1.
三、解答题
13.一辆汽车正常行驶时每小时耗8升,油箱现有52升汽油.
(1)如果汽车行驶时间为t(时),那么油箱中所存油量Q(升)与t(时)的关系式是什么?
(2)油箱中的油总共可供汽车行驶多少小时?
(3)当t的值分别为1,2,3时,Q相应的值是多少?
14.某河流受暴雨影响,水位不断上涨,下面是某天此河流的水位记录:
时间(时) 0 4 8 12 16 20 24
水位(米) 2 2.5 3 4 5 6 8
(1)上表反映的是哪两个量之间的关系?自变量和因变量各是什么?
(2)根据表格画了表示两个变量的折线统计图.
(3)哪段时间水位上升得最快?
15.“十一”黄金周的某一天,小王全家上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离(千米)与小汽车离家后时间(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:
(1)“番茄农庄”离家________千米;
(2)小王全家在“番茄农庄”游玩了________小时;
(3)去时小汽车的平均速度是________千米/小时;
(4)回家时小汽车的平均速度是________千米/小时.
16.一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?
参考答案
1.B
【解析】
【分析】
对于x的每一个值,y都有唯一的值与它对应,则称y是x的函数,据此观察图象可得.
【详解】
解:A,C,D曲线,对于每一个x值,都有2个y值与它对应,因此不符合函数的定义,B中一个x对应一个y值,故B曲线表示y是x的函数.
故答案为:B
【点睛】
本题考查了函数的定义,准确把握定义是解题的关键.
2.C
【解析】
【分析】
分析折线统计图,即可求出答案.
【详解】
解:由折线统计图可知:折线统计图中最底部的数据,则是温度最低的时刻,最高位置的数据则是温度最高的时刻;则清晨5时体温最低,下午5时体温最高;最高温度为37.5℃,最低温度为36.5℃,则小明这一天的体温范围是36.5≤T≤37.5;从5时到17时,小明的体温一直是升高的趋势,而17-24时的体温是下降的趋势.所以错误的是从5时到24时,小明的体温一直是升高的.
故选C.
【点睛】
本题考查了函数的图象,读懂统计图,从图中得到必要的信息是解决本题的关键.
3.B
【解析】
【分析】
一般情况下是把最大的一对数据代入函数关系式后通过比较得出最接近的关系式.
【详解】
解:当m=4时,
A、v=2m-2=6;
B、v=m2-1=15;
C、v=3m-3=9;
D、v=m+1=5.
故选:B.
【点睛】
主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量;解题关键是分别把数据代入下列函数,通过比较找到最符合的函数关系式.
4.A
【解析】
由题意可知,当注水量为0时,水深为0,随着注水量的增加,水深也逐渐增大,所以符合水深y与注水量x之间关系的图象是A.
故选A.
5.A
【解析】
【分析】
根据师生的总费用,可得函数关系式.
【详解】
解:一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为y=10x+30,
故选A.
【点睛】
本题考查了函数关系式,师生的总费用的等量关系是解题关键.
6.B
【解析】
由图表可知,苹果在下落过程中,越来越快,每秒之间速度增加依次为5、15、25、35、45等等,所以观察备选答案B错误.故选B.
7.C
【解析】
试题分析:A.∵由图象可知,在凌晨4点函数图象在最低点﹣3,∴凌晨4时气温最低为﹣3℃,故本选项正确;
B.∵由图象可知,在14点函数图象在最高点8,∴14时气温最高为8℃,故本选项正确;
C.∵由图象可知,从4时至14时,气温随时间增长而上上升,不是从0点,故本选项错误;
D.∵由图象可知,14时至24时,气温随时间增长而下降,故本选项正确.
故选C.
考点:函数的图象.
8.C
【解析】
【分析】
【详解】
试题分析:由于开始以正常速度匀速行驶,接着停下修车,后来加快速度匀驶,所以开始行驶路S是均匀减小的,接着不变,后来速度加快,所以S变化也加快变小,由此即可作出选择.
解:因为开始以正常速度匀速行驶,所以s随着t的增加而增加,随后由于故障修车,此时s不发生改变,再之后加快速度匀驶,s随着t的增加而增加,综上可得S先缓慢增加,再不变,再加速增加.
故选C.
考点:函数的图象.
9.y=24-3x 0<x<8
【解析】
【分析】
由图形可知三角形ABP边BP上的高为AC,利用三角形的面积公式表示出y,即可得到y与x之间的函数关系式;根据关系式结合实际得出自变量的取值范围即可.
【详解】
解:∵BC=8,CP=x,
∴BP=8-x,
∴S△ABP=0.5×BP?AC
=0.5×(8-x)×6
=24-3x,
即y=24-3x;
∵BC=8,根据题意可得自变量的取值范围为:0<x<8.
【点睛】
本题考查了函数与几何知识的综合问题,有些是以函数知识为背景考查几何相关知识,关键是掌握数与形的转化;有些题目是以几何知识为背景,从几何图形中建立函数关系,关键是运用几何知识建立量与量的等式.
10.t=10-6h
【解析】
【分析】
气温=地面温度-降低的气温,把相关数值代入即可.
【详解】
解:∵每升高1千米温度下降6℃,
∴当高度为h时,降低6h,
∴气温t℃与高度h(千米)之间的关系式为t=10-6h.
【点睛】
此题主要考查了一次函数关系式;得到某一高度气温的表示方法是解决本题的关键.
11.80
【解析】
【分析】
先分析出小明家距学校800米,小明从学校步行回家的时间是15-5=10(分),再根据路程、时间、速度的关系即可求得.
【详解】
解:通过读图可知:小明家距学校800米,小明从学校步行回家的时间是15-5=10(分),
所以小明回家的速度是每分钟步行800÷10=80(米).
故答案为:80.
【点睛】
本题主要考查了函数图象,先得出小明家与学校的距离和回家所需要的时间,再求解.
12.②④.
【解析】
【分析】根据各选项的情况,由函数的基本性质进行分析,可得答案.
【详解】(1)因为当x=0时,所以,y==1,即函数图象经过(0,1),故选项①错;
(2)因为当x=±a时,对应的y值相等,即函数图象关于y轴对称,故②正确;
(3)因为中,如果x<0,那么,x越大,y越大,故③错误;
(4)因为当x2最小时,y值最大,即x=0时,y的最大值是1,故④正确.
故答案为②④
【点睛】本题考核知识点:函数性质. 解题关键点:深刻理解函数的基本性质,分析函数的图象与参数之间的关系.
13.(1)Q=52-8t;(2)可供汽车行驶6.5小时;(3)相应的Q=44,36,28.
【解析】
【分析】
(1)存油量=现有油量(52)-消耗的油量,把相关数值代入即可.
(2)把Q=0代入(1)的关系式中求出t即可解;
(3)把t=1,2,3代入()1)的关系式中求出Q即可解.
【详解】
解:(1)∵每小时耗油8升,
∴当时间为t时,耗油8t,
∴油箱中所存油量Q(升)与t(时)的关系式为 Q=52-8t;
(2)当Q=0时,52-8t=0,解得t=6.5,
即油箱中的油总共可供汽车行驶6.5小时;
(3)t=1,2,3,相应的Q=44,36,28.
【点睛】
此题主要考查了一次函数关系式;得到某一时刻存油量的表示方法是解决本题的关键.
14.(1)时间和水位之间的关系,时间是自变量,水位是因变量;(2)见解析;(3)20-24水位上升最快.
【解析】
【分析】
(1)根据表格可知是时间和水位之间的关系,在函数中,给一个变量x一个值,另一个变量y就有对应的值,则x是自变量,y是因变量,据此即可判断;
(2)根据表格中水位随时间的变化记录画图;
(3)相同的时间上升的水位越多代表上升的越快,根据此规律看表数据即可判断.
【详解】
解:(1)根据表格可知是时间和水位之间的关系,并且每过4个小时水位在变化,可知水位随着时间在变化,即时间是自变量,水位是因变量;
(2)见下图:
(3)0-4时的变化情况为2.5-2=0.5m;
4-8时的变化情况为3-2.5=0.5m;
8-12时的变化情况为4-3=1m;
12-16时的变化情况为5-4=1m;
16-20时的变化情况为6-5=1m;
20-24时的变化情况为8-6=2m;
∴20-24水位上升最快.
【点睛】
考查水位变化情况和频率分布折线图,解题的关键是能够读懂表格,并作出折线统计图,难度不大.
15.(1)180;(2)4;(3)90;(4)60
【解析】
【分析】
(1)根据s轴上的最高点即可确定答案;
(2)根据s轴上不变的时间即可解答;
(3)根据去时路程除以去的时间即得答案;
(4)根据图象上14-15时所走的路程解答即可.
【详解】
解:(1)由图可知:“番茄农庄”离家180千米;
(2)14-10=4小时,所以小王全家在“番茄农庄”游玩了4小时;
(3)千米/小时,所以去时小汽车的平均速度是90千米/小时;
(4)由图象可得:14-15时,汽车行驶了(180-120)=60千米,所以回家时小汽车的平均速度是60千米/小时.
故答案为:180;4;90;60.
【点睛】
本题考查了函数的图象,读懂图象提供的信息、正确理解横、纵坐标的含义是解题的关键.
16.(1)该一次函数解析式为y=﹣x+60.(2)在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是10千米.
【解析】
【分析】(1)根据函数图象中点的坐标利用待定系数法求出一次函数解析式;
(2)根据一次函数图象上点的坐标特征即可求出剩余油量为8升时行驶的路程,即可求得答案.
【详解】(1)设该一次函数解析式为y=kx+b,
将(150,45)、(0,60)代入y=kx+b中,得
,解得:,
∴该一次函数解析式为y=﹣x+60;
(2)当y=﹣x+60=8时,
解得x=520,
即行驶520千米时,油箱中的剩余油量为8升.
530﹣520=10千米,
油箱中的剩余油量为8升时,距离加油站10千米,
∴在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是10千米.
【点睛】本题考查了一次函数的应用,熟练掌握待定系数法,弄清题意是解题的关键.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
19.1.2函数的图象
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各曲线中,表示是的函数是( )
A.B.
C. D.
2.正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同,下图反映了一天24小时内小明体温的变化情况,下列说法错误的是( )
A.清晨5时体温最低 B.下午5时体温最高
C.从5时至24时,小明体温一直是升高的 D.从0时至5时,小明体温一直是下降的
3.在某次试验中,测得两个变量m和v之间的4组对应数据如下表:
?则m与v之间的关系最接近于下列各关系式中的 ( )
A.v=2m-2 B.v=m2-1 C.v=3m-3 D.v=m+1
4.如图所示,向高为h的圆柱形水杯注水,已知水杯底面半径为2,那么水深y与注水量x之间关系的图象是( )
A.(A) B.(B) C.(C) D.(D)
5.一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为( )
A.y=10x+30 B.y=40x C.y=10+30x D.y=20x
6.某学习小组做了一个实验:从一幢100 m高的楼顶随手放下一只苹果,测得有关数据如下:
下落时间t(s) 1 2 3 4
下落高度h(m) 5 20 45 80
则下列说法错误的是( )
A.苹果每秒下落的路程越来越长 B.苹果每秒下落的路程不变
C.苹果下落的速度越来越快 D.可以推测,苹果落到地面的时间不超过5秒
7.如图,是一台自动测温仪记录的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
A.凌晨4时气温最低为-3℃
B.14时气温最高为8℃
C.从0时至14时,气温随时间增长而上升
D.从14时至24时,气温随时间增长而下降
8.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()
A. B. C. D.
二、填空题
9.在中,∠C=90°,AC=6,BC=8,设P是BC上任一点,P点与B、C不重合,且,若,则与之间的函数关系式是_____,自变量取值范围为_____.
10.在地球表面的一定高度内,每升高1千米,温度下降.已知地面温度为,设高度为h千米时的温度是t,则t与h之间的关系是________________
11.小明从家跑步到学校,接着马上原路步行回家.如图所示为小明离家的路程与时间的图像,则小明回家的速度是每分钟步行________m.
12.已知函数y=,下列关于它的图象与性质,正确的是____.(写出所有正确的序号)
①函数图象与坐标轴无交点; ②函数图象关于y轴对称;
③y随x的增大而减小; ④函数有最大值1.
三、解答题
13.一辆汽车正常行驶时每小时耗8升,油箱现有52升汽油.
(1)如果汽车行驶时间为t(时),那么油箱中所存油量Q(升)与t(时)的关系式是什么?
(2)油箱中的油总共可供汽车行驶多少小时?
(3)当t的值分别为1,2,3时,Q相应的值是多少?
14.某河流受暴雨影响,水位不断上涨,下面是某天此河流的水位记录:
时间(时) 0 4 8 12 16 20 24
水位(米) 2 2.5 3 4 5 6 8
(1)上表反映的是哪两个量之间的关系?自变量和因变量各是什么?
(2)根据表格画了表示两个变量的折线统计图.
(3)哪段时间水位上升得最快?
15.“十一”黄金周的某一天,小王全家上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离(千米)与小汽车离家后时间(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:
(1)“番茄农庄”离家________千米;
(2)小王全家在“番茄农庄”游玩了________小时;
(3)去时小汽车的平均速度是________千米/小时;
(4)回家时小汽车的平均速度是________千米/小时.
16.一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?
参考答案
1.B
【解析】
【分析】
对于x的每一个值,y都有唯一的值与它对应,则称y是x的函数,据此观察图象可得.
【详解】
解:A,C,D曲线,对于每一个x值,都有2个y值与它对应,因此不符合函数的定义,B中一个x对应一个y值,故B曲线表示y是x的函数.
故答案为:B
【点睛】
本题考查了函数的定义,准确把握定义是解题的关键.
2.C
【解析】
【分析】
分析折线统计图,即可求出答案.
【详解】
解:由折线统计图可知:折线统计图中最底部的数据,则是温度最低的时刻,最高位置的数据则是温度最高的时刻;则清晨5时体温最低,下午5时体温最高;最高温度为37.5℃,最低温度为36.5℃,则小明这一天的体温范围是36.5≤T≤37.5;从5时到17时,小明的体温一直是升高的趋势,而17-24时的体温是下降的趋势.所以错误的是从5时到24时,小明的体温一直是升高的.
故选C.
【点睛】
本题考查了函数的图象,读懂统计图,从图中得到必要的信息是解决本题的关键.
3.B
【解析】
【分析】
一般情况下是把最大的一对数据代入函数关系式后通过比较得出最接近的关系式.
【详解】
解:当m=4时,
A、v=2m-2=6;
B、v=m2-1=15;
C、v=3m-3=9;
D、v=m+1=5.
故选:B.
【点睛】
主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量;解题关键是分别把数据代入下列函数,通过比较找到最符合的函数关系式.
4.A
【解析】
由题意可知,当注水量为0时,水深为0,随着注水量的增加,水深也逐渐增大,所以符合水深y与注水量x之间关系的图象是A.
故选A.
5.A
【解析】
【分析】
根据师生的总费用,可得函数关系式.
【详解】
解:一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为y=10x+30,
故选A.
【点睛】
本题考查了函数关系式,师生的总费用的等量关系是解题关键.
6.B
【解析】
由图表可知,苹果在下落过程中,越来越快,每秒之间速度增加依次为5、15、25、35、45等等,所以观察备选答案B错误.故选B.
7.C
【解析】
试题分析:A.∵由图象可知,在凌晨4点函数图象在最低点﹣3,∴凌晨4时气温最低为﹣3℃,故本选项正确;
B.∵由图象可知,在14点函数图象在最高点8,∴14时气温最高为8℃,故本选项正确;
C.∵由图象可知,从4时至14时,气温随时间增长而上上升,不是从0点,故本选项错误;
D.∵由图象可知,14时至24时,气温随时间增长而下降,故本选项正确.
故选C.
考点:函数的图象.
8.C
【解析】
【分析】
【详解】
试题分析:由于开始以正常速度匀速行驶,接着停下修车,后来加快速度匀驶,所以开始行驶路S是均匀减小的,接着不变,后来速度加快,所以S变化也加快变小,由此即可作出选择.
解:因为开始以正常速度匀速行驶,所以s随着t的增加而增加,随后由于故障修车,此时s不发生改变,再之后加快速度匀驶,s随着t的增加而增加,综上可得S先缓慢增加,再不变,再加速增加.
故选C.
考点:函数的图象.
9.y=24-3x 0<x<8
【解析】
【分析】
由图形可知三角形ABP边BP上的高为AC,利用三角形的面积公式表示出y,即可得到y与x之间的函数关系式;根据关系式结合实际得出自变量的取值范围即可.
【详解】
解:∵BC=8,CP=x,
∴BP=8-x,
∴S△ABP=0.5×BP?AC
=0.5×(8-x)×6
=24-3x,
即y=24-3x;
∵BC=8,根据题意可得自变量的取值范围为:0<x<8.
【点睛】
本题考查了函数与几何知识的综合问题,有些是以函数知识为背景考查几何相关知识,关键是掌握数与形的转化;有些题目是以几何知识为背景,从几何图形中建立函数关系,关键是运用几何知识建立量与量的等式.
10.t=10-6h
【解析】
【分析】
气温=地面温度-降低的气温,把相关数值代入即可.
【详解】
解:∵每升高1千米温度下降6℃,
∴当高度为h时,降低6h,
∴气温t℃与高度h(千米)之间的关系式为t=10-6h.
【点睛】
此题主要考查了一次函数关系式;得到某一高度气温的表示方法是解决本题的关键.
11.80
【解析】
【分析】
先分析出小明家距学校800米,小明从学校步行回家的时间是15-5=10(分),再根据路程、时间、速度的关系即可求得.
【详解】
解:通过读图可知:小明家距学校800米,小明从学校步行回家的时间是15-5=10(分),
所以小明回家的速度是每分钟步行800÷10=80(米).
故答案为:80.
【点睛】
本题主要考查了函数图象,先得出小明家与学校的距离和回家所需要的时间,再求解.
12.②④.
【解析】
【分析】根据各选项的情况,由函数的基本性质进行分析,可得答案.
【详解】(1)因为当x=0时,所以,y==1,即函数图象经过(0,1),故选项①错;
(2)因为当x=±a时,对应的y值相等,即函数图象关于y轴对称,故②正确;
(3)因为中,如果x<0,那么,x越大,y越大,故③错误;
(4)因为当x2最小时,y值最大,即x=0时,y的最大值是1,故④正确.
故答案为②④
【点睛】本题考核知识点:函数性质. 解题关键点:深刻理解函数的基本性质,分析函数的图象与参数之间的关系.
13.(1)Q=52-8t;(2)可供汽车行驶6.5小时;(3)相应的Q=44,36,28.
【解析】
【分析】
(1)存油量=现有油量(52)-消耗的油量,把相关数值代入即可.
(2)把Q=0代入(1)的关系式中求出t即可解;
(3)把t=1,2,3代入()1)的关系式中求出Q即可解.
【详解】
解:(1)∵每小时耗油8升,
∴当时间为t时,耗油8t,
∴油箱中所存油量Q(升)与t(时)的关系式为 Q=52-8t;
(2)当Q=0时,52-8t=0,解得t=6.5,
即油箱中的油总共可供汽车行驶6.5小时;
(3)t=1,2,3,相应的Q=44,36,28.
【点睛】
此题主要考查了一次函数关系式;得到某一时刻存油量的表示方法是解决本题的关键.
14.(1)时间和水位之间的关系,时间是自变量,水位是因变量;(2)见解析;(3)20-24水位上升最快.
【解析】
【分析】
(1)根据表格可知是时间和水位之间的关系,在函数中,给一个变量x一个值,另一个变量y就有对应的值,则x是自变量,y是因变量,据此即可判断;
(2)根据表格中水位随时间的变化记录画图;
(3)相同的时间上升的水位越多代表上升的越快,根据此规律看表数据即可判断.
【详解】
解:(1)根据表格可知是时间和水位之间的关系,并且每过4个小时水位在变化,可知水位随着时间在变化,即时间是自变量,水位是因变量;
(2)见下图:
(3)0-4时的变化情况为2.5-2=0.5m;
4-8时的变化情况为3-2.5=0.5m;
8-12时的变化情况为4-3=1m;
12-16时的变化情况为5-4=1m;
16-20时的变化情况为6-5=1m;
20-24时的变化情况为8-6=2m;
∴20-24水位上升最快.
【点睛】
考查水位变化情况和频率分布折线图,解题的关键是能够读懂表格,并作出折线统计图,难度不大.
15.(1)180;(2)4;(3)90;(4)60
【解析】
【分析】
(1)根据s轴上的最高点即可确定答案;
(2)根据s轴上不变的时间即可解答;
(3)根据去时路程除以去的时间即得答案;
(4)根据图象上14-15时所走的路程解答即可.
【详解】
解:(1)由图可知:“番茄农庄”离家180千米;
(2)14-10=4小时,所以小王全家在“番茄农庄”游玩了4小时;
(3)千米/小时,所以去时小汽车的平均速度是90千米/小时;
(4)由图象可得:14-15时,汽车行驶了(180-120)=60千米,所以回家时小汽车的平均速度是60千米/小时.
故答案为:180;4;90;60.
【点睛】
本题考查了函数的图象,读懂图象提供的信息、正确理解横、纵坐标的含义是解题的关键.
16.(1)该一次函数解析式为y=﹣x+60.(2)在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是10千米.
【解析】
【分析】(1)根据函数图象中点的坐标利用待定系数法求出一次函数解析式;
(2)根据一次函数图象上点的坐标特征即可求出剩余油量为8升时行驶的路程,即可求得答案.
【详解】(1)设该一次函数解析式为y=kx+b,
将(150,45)、(0,60)代入y=kx+b中,得
,解得:,
∴该一次函数解析式为y=﹣x+60;
(2)当y=﹣x+60=8时,
解得x=520,
即行驶520千米时,油箱中的剩余油量为8升.
530﹣520=10千米,
油箱中的剩余油量为8升时,距离加油站10千米,
∴在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是10千米.
【点睛】本题考查了一次函数的应用,熟练掌握待定系数法,弄清题意是解题的关键.
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
