19.2.2一次函数 同步练习(含详解)
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
19.2.2一次函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.将直线y=2x向上平移两个单位,所得的直线是
A.y=2x+2 B.y=2x-2 C.y=2(x-2) D.y=2(x+2)
2.要得到函数y2x3的图象,只需将函数y2x的图象( )
A.向左平移3个单位 B.向右平移3个单位
C.向下平移3个单位 D.向上平移3个单位
3.若且,则函数的图象可能是( )
A. B.
C. D.
4.下列函数中,y是x的正比例函数的是( )
A.y=4x+1 B.y=2x2 C.y=-x D.y=
5.已知一次函数y=(k+1)x+b的图象如图所示,则k的取值范围是( )
A.k<0 B.k<﹣1 C.k<1 D.k>﹣1
6.一次函数的图象大致是( )
A. B. C.D.
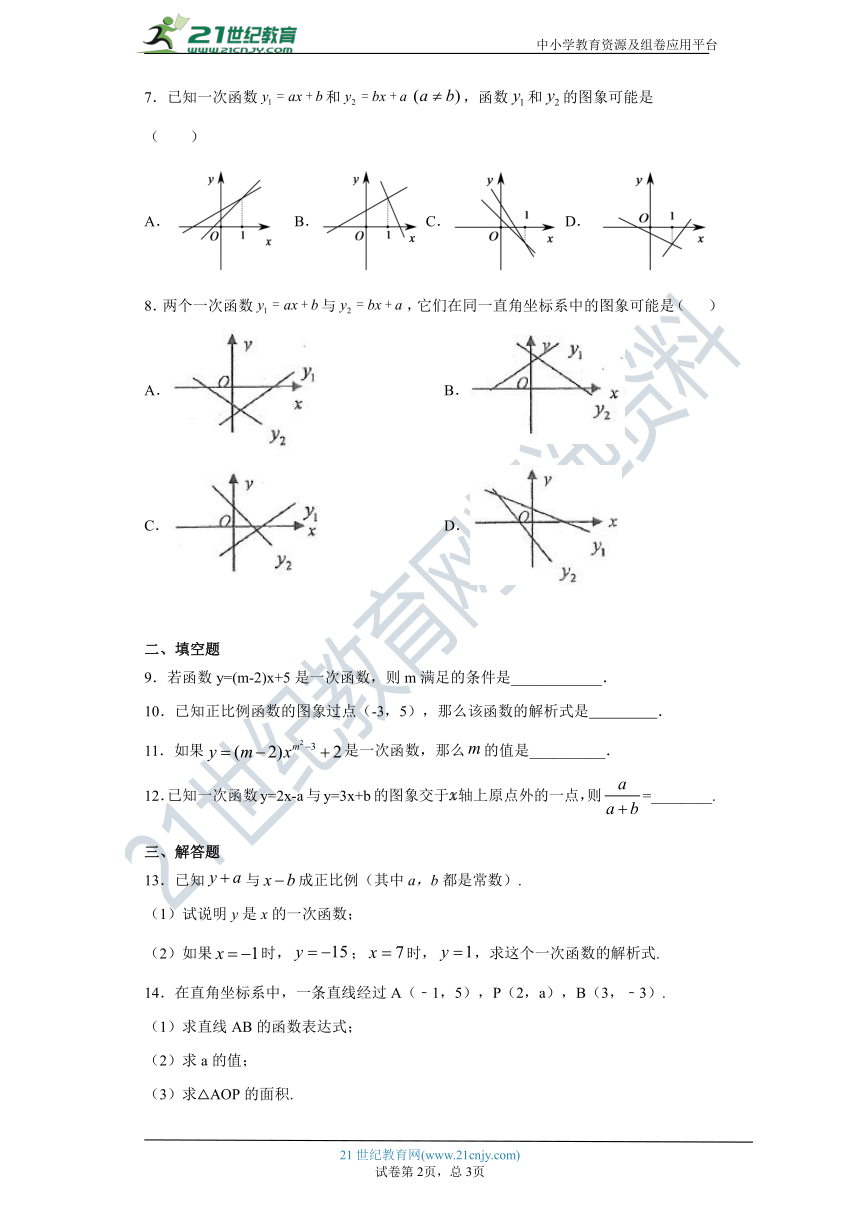
7.已知一次函数和,函数和的图象可能是 ( )
A. B.C.D.
8.两个一次函数与,它们在同一直角坐标系中的图象可能是( )
A. B.
C. D.
二、填空题
9.若函数y=(m-2)x+5是一次函数,则m满足的条件是____________.
10.已知正比例函数的图象过点(-3,5),那么该函数的解析式是 .
11.如果是一次函数,那么的值是__________.
12.已知一次函数y=2x-a与y=3x+b的图象交于轴上原点外的一点,则=________.
三、解答题
13.已知与成正比例(其中a,b都是常数).
(1)试说明y是x的一次函数;
(2)如果时,;时,,求这个一次函数的解析式.
14.在直角坐标系中,一条直线经过A(﹣1,5),P(2,a),B(3,﹣3).
(1)求直线AB的函数表达式;
(2)求a的值;
(3)求△AOP的面积.
15.如图,已知,一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的解析式;
(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图象上.
16.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
参考答案
1.A
解析:
平移时k的值不变,只有b发生变化
原直线的k=2,b=0;向上平移两个单位得到了新直线,
那么新直线的k=2,b=0+2=2.
∴新直线的解析式为y=2x+2.
故选A.
2.D
解析:
平移后相当于x不变y增加了3个单位,由此可得出答案.
详解:
解:由题意得x值不变y增加3个单位
应向上平移3个单位.
故选D.
点睛:
本题考查一次函数图象的几何变换,注意平移k值不变的性质.
3.A
解析:
根据且,得到a,b的取值,再根据一次函数的图像即可求解.
详解:
解:∵,且,
∴a>0,b<0.
∴函数的图象经过第一、三、四象限.
故选A.
点睛:
此题主要考查一次函数的图像,解题的关键是熟知不等式的性质及一次函数的图像.
4.C
解析:
正比例函数的解析式是,据此解题.
详解:
A.y=4x+1是一次函数,不是正比例函数,故A错误;
B. y=2x2是二次函数,不是正比例函数,故B错误;
C.y=-x是正比例函数,故C正确;
D. y=是根式函数,不是正比例函数,故D错误.
故选C.
点睛:
本题考查正比例函数、一次函数、二次函数等的概念,是基础考点,难度容易,掌握相关知识是解题关键.
5.B
解析:
根据一次函数的增减性确定有关k的不等式,求解即可.
详解:
∵观察图象知:y随x的增大而减小,
∴k+1<0,
解得:k<﹣1,
故选B.
点睛:
考查了一次函数的图象与系数的关系,解题的关键是了解系数对函数图象的影响,难度不大.
6.D
解析:
根据一次函数的图象与系数的关系选出正确选项.
详解:
解:根据函数解析式,
∵,∴直线斜向下,
∵,∴直线经过y轴负半轴,
图象经过二、三、四象限.
故选:D.
点睛:
本题考查一次函数的图象,解题的关键是能够根据解析式系数的正负判断图象的形状.
7.A
解析:
根据一次函数图形的性质,结合题意和,即可得到答案.
详解:
①当,、的图象都经过一、二、三象限
②当,、的图象都经过二、三、四象限
③当,的图象都经过一、三、四象限,的图象都经过一、二、四象限
④当,的图象都经过一、二、四象限,的图象都经过一、三、四象限
满足题意的只有A.
故选A.
点睛:
本题考查一次函数图像,解题的关键是熟练掌握一次函数图像的性质.
8.C
解析:
根据函数图象判断a、b的符号,两个函数的图象符号相同即是正确,否则不正确.
详解:
A、若a>0,b<0,符合,不符合,故不符合题意;
B、若a>0,b>0,符合,不符合,故不符合题意;
C、若a>0,b<0,符合,符合,故符合题意;
D、若a<0,b>0,符合,不符合,故不符合题意;
故选:C.
点睛:
此题考查一次函数的性质,能根据一次函数的解析式y=kx+b中k、b的符号判断函数图象所经过的象限,当k>0时函数图象过一、三象限,k<0时函数图象过二、四象限;当b>0时与y轴正半轴相交,b<0时与y轴负半轴相交.
9.m≠2.
解析:
根据一次函数的定义求解即可.
详解:
解:∵函数y=(m-2)x+5是一次函数,
∴m﹣2≠0,即m≠2.
故答案为m≠2.
点睛:
本题考查一次函数的定义. 一次函数解析式 y=kx+b 的结构特征:
(1)k是常数,k≠0 ;(2)自变量x的次数是1;(3)常数项b可以为任意实数.
10.y=
解析:
由题意知该函数的形式为y=kx.将题目中的已知数字代入即可求得.
详解:
设y=kx.将(-3,5)代入,得
-3k=5,得,
所以
点睛:
考点:正比例函数的定义.要求考生掌握书本中概念.
11.-2
解析:
根据一次函数的定义:形如(k,b是常数,k≠0)的函数,叫做一次函数,即可求得的值.
详解:
解:由是一次函数,
可得:,
解得: .
故填.
点睛:
本题考查一次函数的定义,熟记一次函数的一般形式.
12.-2
解析:
详解:
在一次函数y=2x?a中,令y=0,得到x=,
在一次函数y=3x+b中,令y=0,得到x=?,
由题意得:=?,图象交于x轴上原点外一点,则a≠0,且b≠0,
可以设=?=k,则a=2k,b=?3k,
代入=?2.
故答案为?2.
13.(1)见解析;(2)
解析:
(1)设(,k、b、a为常数),化简后根据一次函数的定义即可说明;
(2)设这个一次函数的解析式为,利用待定系数法即可求出一次函数的解析式.
详解:
(1)由题意可设(,k、b、a为常数),
化简得(为常数)
故y是x的一次函数.
(2)设这个一次函数的解析式为
由题意可得,解得,
故这个一次函数的解析式为.
点睛:
此题考查的是一次函数的判断和求一次函数的解析式,掌握一次函数的定义和用待定系数法求一次函数的解析式是解决此题的关键.
14.(1)y=﹣2x+3;(2)a=﹣1;(3)4.5.
解析:
(1)根据点A、B的坐标利用待定系数法即可求出直线AB的解析式;
(2)利用一次函数图象上点的坐标即可求出a值;
(3)设AB与y轴交与点D,将x=0代入直线AB的解析式中求出点D的坐标,再根据S△AOP=S△AOD+S△POD利用三角形的面积公式即可得出结论.
详解:
解:(1)设直线AB的函数表达式为y=kx+b,把点A、B的坐标代入得:,
解得:k=﹣2,b=3,所以直线AB的函数解析式为y=﹣2x+3;
(2)把P(2,a)代入y=﹣2x+3得:a=﹣1;
(3)
∵把x=0代入y=﹣2x+3得:y=3,
∴直线y=﹣2x+3与y轴的交点为(0,3),即OD=3,
∵P(2,﹣1),
∴△AOP的面积=△AOD的面积+△DOP的面积=+=4.5.
故答案为:(1)y=﹣2x+3;(2)a=﹣1;(3)4.5.
点睛:
本题考查一次函数图象上点的坐标特征.
15.(1) y=x+3;(2)见解析
解析:
(1)将A点坐标代入解析式y=kx+3即可求得k值,从而得一次函数解析式;
(2)分别把各点的坐标代入解析式即可判定.
详解:
(1)由题意得,
k+3=4,
解得,k=1,
所以,该一次函数的解析式是:y=x+3;
(2)由(1)知,一次函数的解析式是y=x+3.
当x=-1时,y=2,
∴点B(-1,5)不在该一次函数图象上;
当x=0时,y=3,
∴点C(0,3)在该一次函数图象上;
当x=2时,y=5,
∴点D(2,1)不在该一次函数图象上.
16.(1)直线AB的解析式为y=2x﹣2,
(2)点C的坐标是(2,2).
解析:
待定系数法,直线上点的坐标与方程的.
(1)设直线AB的解析式为y=kx+b,将点A(1,0)、点B(0,﹣2)分别代入解析式即可组成方程组,从而得到AB的解析式.
(2)设点C的坐标为(x,y),根据三角形面积公式以及S△BOC=2求出C的横坐标,再代入直线即可求出y的值,从而得到其坐标.
详解:
解:(1)设直线AB的解析式为y=kx+b,
∵直线AB过点A(1,0)、点B(0,﹣2),
∴,解得.
∴直线AB的解析式为y=2x﹣2.
(2)设点C的坐标为(x,y),
∵S△BOC=2,∴?2?x=2,解得x=2.
∴y=2×2﹣2=2.
∴点C的坐标是(2,2).
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
中小学教育资源及组卷应用平台
19.2.2一次函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.将直线y=2x向上平移两个单位,所得的直线是
A.y=2x+2 B.y=2x-2 C.y=2(x-2) D.y=2(x+2)
2.要得到函数y2x3的图象,只需将函数y2x的图象( )
A.向左平移3个单位 B.向右平移3个单位
C.向下平移3个单位 D.向上平移3个单位
3.若且,则函数的图象可能是( )
A. B.
C. D.
4.下列函数中,y是x的正比例函数的是( )
A.y=4x+1 B.y=2x2 C.y=-x D.y=
5.已知一次函数y=(k+1)x+b的图象如图所示,则k的取值范围是( )
A.k<0 B.k<﹣1 C.k<1 D.k>﹣1
6.一次函数的图象大致是( )
A. B. C.D.
7.已知一次函数和,函数和的图象可能是 ( )
A. B.C.D.
8.两个一次函数与,它们在同一直角坐标系中的图象可能是( )
A. B.
C. D.
二、填空题
9.若函数y=(m-2)x+5是一次函数,则m满足的条件是____________.
10.已知正比例函数的图象过点(-3,5),那么该函数的解析式是 .
11.如果是一次函数,那么的值是__________.
12.已知一次函数y=2x-a与y=3x+b的图象交于轴上原点外的一点,则=________.
三、解答题
13.已知与成正比例(其中a,b都是常数).
(1)试说明y是x的一次函数;
(2)如果时,;时,,求这个一次函数的解析式.
14.在直角坐标系中,一条直线经过A(﹣1,5),P(2,a),B(3,﹣3).
(1)求直线AB的函数表达式;
(2)求a的值;
(3)求△AOP的面积.
15.如图,已知,一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的解析式;
(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图象上.
16.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
参考答案
1.A
解析:
平移时k的值不变,只有b发生变化
原直线的k=2,b=0;向上平移两个单位得到了新直线,
那么新直线的k=2,b=0+2=2.
∴新直线的解析式为y=2x+2.
故选A.
2.D
解析:
平移后相当于x不变y增加了3个单位,由此可得出答案.
详解:
解:由题意得x值不变y增加3个单位
应向上平移3个单位.
故选D.
点睛:
本题考查一次函数图象的几何变换,注意平移k值不变的性质.
3.A
解析:
根据且,得到a,b的取值,再根据一次函数的图像即可求解.
详解:
解:∵,且,
∴a>0,b<0.
∴函数的图象经过第一、三、四象限.
故选A.
点睛:
此题主要考查一次函数的图像,解题的关键是熟知不等式的性质及一次函数的图像.
4.C
解析:
正比例函数的解析式是,据此解题.
详解:
A.y=4x+1是一次函数,不是正比例函数,故A错误;
B. y=2x2是二次函数,不是正比例函数,故B错误;
C.y=-x是正比例函数,故C正确;
D. y=是根式函数,不是正比例函数,故D错误.
故选C.
点睛:
本题考查正比例函数、一次函数、二次函数等的概念,是基础考点,难度容易,掌握相关知识是解题关键.
5.B
解析:
根据一次函数的增减性确定有关k的不等式,求解即可.
详解:
∵观察图象知:y随x的增大而减小,
∴k+1<0,
解得:k<﹣1,
故选B.
点睛:
考查了一次函数的图象与系数的关系,解题的关键是了解系数对函数图象的影响,难度不大.
6.D
解析:
根据一次函数的图象与系数的关系选出正确选项.
详解:
解:根据函数解析式,
∵,∴直线斜向下,
∵,∴直线经过y轴负半轴,
图象经过二、三、四象限.
故选:D.
点睛:
本题考查一次函数的图象,解题的关键是能够根据解析式系数的正负判断图象的形状.
7.A
解析:
根据一次函数图形的性质,结合题意和,即可得到答案.
详解:
①当,、的图象都经过一、二、三象限
②当,、的图象都经过二、三、四象限
③当,的图象都经过一、三、四象限,的图象都经过一、二、四象限
④当,的图象都经过一、二、四象限,的图象都经过一、三、四象限
满足题意的只有A.
故选A.
点睛:
本题考查一次函数图像,解题的关键是熟练掌握一次函数图像的性质.
8.C
解析:
根据函数图象判断a、b的符号,两个函数的图象符号相同即是正确,否则不正确.
详解:
A、若a>0,b<0,符合,不符合,故不符合题意;
B、若a>0,b>0,符合,不符合,故不符合题意;
C、若a>0,b<0,符合,符合,故符合题意;
D、若a<0,b>0,符合,不符合,故不符合题意;
故选:C.
点睛:
此题考查一次函数的性质,能根据一次函数的解析式y=kx+b中k、b的符号判断函数图象所经过的象限,当k>0时函数图象过一、三象限,k<0时函数图象过二、四象限;当b>0时与y轴正半轴相交,b<0时与y轴负半轴相交.
9.m≠2.
解析:
根据一次函数的定义求解即可.
详解:
解:∵函数y=(m-2)x+5是一次函数,
∴m﹣2≠0,即m≠2.
故答案为m≠2.
点睛:
本题考查一次函数的定义. 一次函数解析式 y=kx+b 的结构特征:
(1)k是常数,k≠0 ;(2)自变量x的次数是1;(3)常数项b可以为任意实数.
10.y=
解析:
由题意知该函数的形式为y=kx.将题目中的已知数字代入即可求得.
详解:
设y=kx.将(-3,5)代入,得
-3k=5,得,
所以
点睛:
考点:正比例函数的定义.要求考生掌握书本中概念.
11.-2
解析:
根据一次函数的定义:形如(k,b是常数,k≠0)的函数,叫做一次函数,即可求得的值.
详解:
解:由是一次函数,
可得:,
解得: .
故填.
点睛:
本题考查一次函数的定义,熟记一次函数的一般形式.
12.-2
解析:
详解:
在一次函数y=2x?a中,令y=0,得到x=,
在一次函数y=3x+b中,令y=0,得到x=?,
由题意得:=?,图象交于x轴上原点外一点,则a≠0,且b≠0,
可以设=?=k,则a=2k,b=?3k,
代入=?2.
故答案为?2.
13.(1)见解析;(2)
解析:
(1)设(,k、b、a为常数),化简后根据一次函数的定义即可说明;
(2)设这个一次函数的解析式为,利用待定系数法即可求出一次函数的解析式.
详解:
(1)由题意可设(,k、b、a为常数),
化简得(为常数)
故y是x的一次函数.
(2)设这个一次函数的解析式为
由题意可得,解得,
故这个一次函数的解析式为.
点睛:
此题考查的是一次函数的判断和求一次函数的解析式,掌握一次函数的定义和用待定系数法求一次函数的解析式是解决此题的关键.
14.(1)y=﹣2x+3;(2)a=﹣1;(3)4.5.
解析:
(1)根据点A、B的坐标利用待定系数法即可求出直线AB的解析式;
(2)利用一次函数图象上点的坐标即可求出a值;
(3)设AB与y轴交与点D,将x=0代入直线AB的解析式中求出点D的坐标,再根据S△AOP=S△AOD+S△POD利用三角形的面积公式即可得出结论.
详解:
解:(1)设直线AB的函数表达式为y=kx+b,把点A、B的坐标代入得:,
解得:k=﹣2,b=3,所以直线AB的函数解析式为y=﹣2x+3;
(2)把P(2,a)代入y=﹣2x+3得:a=﹣1;
(3)
∵把x=0代入y=﹣2x+3得:y=3,
∴直线y=﹣2x+3与y轴的交点为(0,3),即OD=3,
∵P(2,﹣1),
∴△AOP的面积=△AOD的面积+△DOP的面积=+=4.5.
故答案为:(1)y=﹣2x+3;(2)a=﹣1;(3)4.5.
点睛:
本题考查一次函数图象上点的坐标特征.
15.(1) y=x+3;(2)见解析
解析:
(1)将A点坐标代入解析式y=kx+3即可求得k值,从而得一次函数解析式;
(2)分别把各点的坐标代入解析式即可判定.
详解:
(1)由题意得,
k+3=4,
解得,k=1,
所以,该一次函数的解析式是:y=x+3;
(2)由(1)知,一次函数的解析式是y=x+3.
当x=-1时,y=2,
∴点B(-1,5)不在该一次函数图象上;
当x=0时,y=3,
∴点C(0,3)在该一次函数图象上;
当x=2时,y=5,
∴点D(2,1)不在该一次函数图象上.
16.(1)直线AB的解析式为y=2x﹣2,
(2)点C的坐标是(2,2).
解析:
待定系数法,直线上点的坐标与方程的.
(1)设直线AB的解析式为y=kx+b,将点A(1,0)、点B(0,﹣2)分别代入解析式即可组成方程组,从而得到AB的解析式.
(2)设点C的坐标为(x,y),根据三角形面积公式以及S△BOC=2求出C的横坐标,再代入直线即可求出y的值,从而得到其坐标.
详解:
解:(1)设直线AB的解析式为y=kx+b,
∵直线AB过点A(1,0)、点B(0,﹣2),
∴,解得.
∴直线AB的解析式为y=2x﹣2.
(2)设点C的坐标为(x,y),
∵S△BOC=2,∴?2?x=2,解得x=2.
∴y=2×2﹣2=2.
∴点C的坐标是(2,2).
_21?????????è?????(www.21cnjy.com)_试卷第1 11页,总3 33页
_21?????????è?????(www.21cnjy.com)_
