2020-2021学年华东师大新版九年级上册数学《第24章 解直角三角形》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年华东师大新版九年级上册数学《第24章 解直角三角形》单元测试卷(Word版 含解析) | 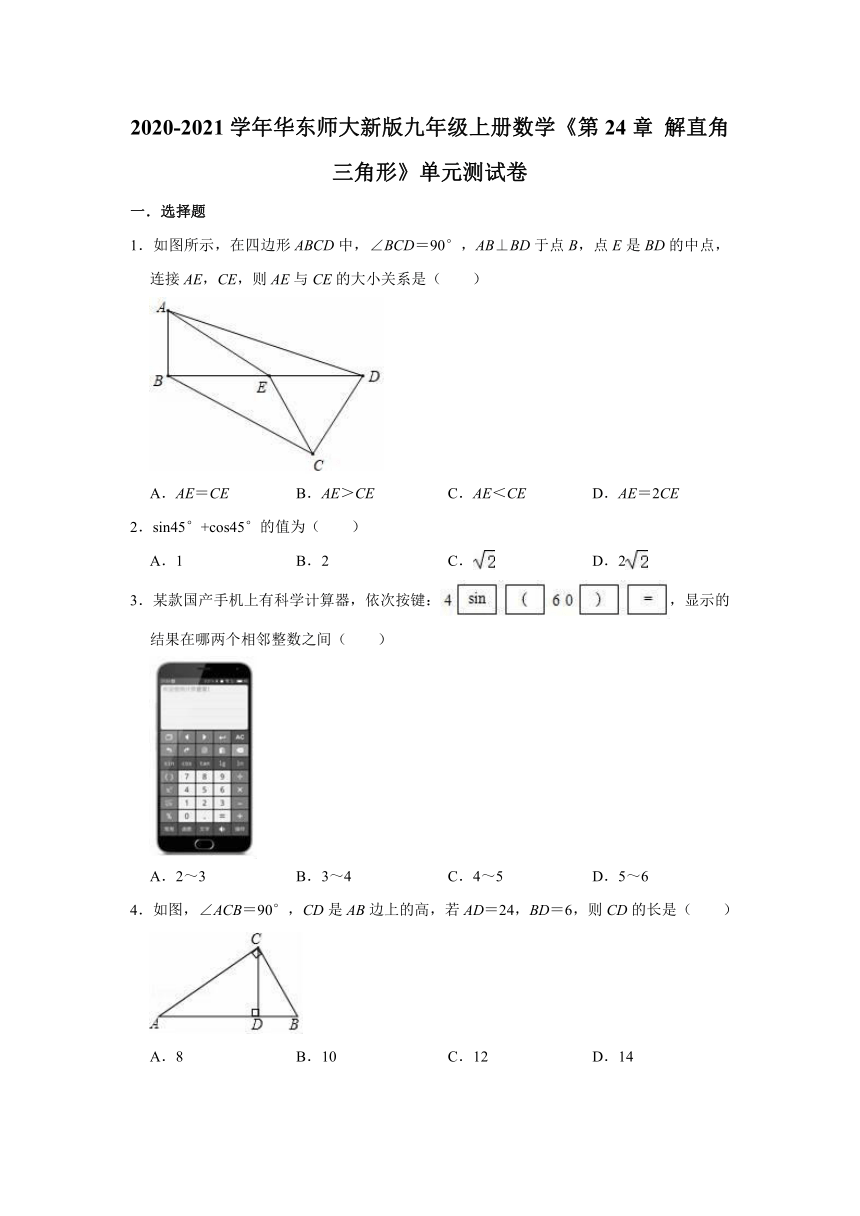 | |
| 格式 | zip | ||
| 文件大小 | 349.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-18 20:57:44 | ||
图片预览




文档简介
2020-2021学年华东师大新版九年级上册数学《第24章
解直角三角形》单元测试卷
一.选择题
1.如图所示,在四边形ABCD中,∠BCD=90°,AB⊥BD于点B,点E是BD的中点,连接AE,CE,则AE与CE的大小关系是( )
A.AE=CE
B.AE>CE
C.AE<CE
D.AE=2CE
2.sin45°+cos45°的值为( )
A.1
B.2
C.
D.2
3.某款国产手机上有科学计算器,依次按键:,显示的结果在哪两个相邻整数之间( )
A.2~3
B.3~4
C.4~5
D.5~6
4.如图,∠ACB=90°,CD是AB边上的高,若AD=24,BD=6,则CD的长是( )
A.8
B.10
C.12
D.14
5.如图,在Rt△ABC中,∠A=90°,sinB=,AC=2,则BC长为( )
A.2
B.4
C.6
D.8
6.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,AD=2,则BD=( )
A.2
B.4
C.6
D.8
7.式子sin210°+sin220°+cos210°+cos220°的值为( )
A.1
B.2
C.3
D.4
8.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点D到OB的距离等于( )
A.asinx+bsinx
B.acosx+bcosx
C.asinx+bcosx
D.acosx+bsinx
9.在下列条件中:①∠A=∠B﹣∠C,②∠A﹣∠B=90°,③∠A=∠B=2∠C,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
10.如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=,tan∠BA3C=…,依此规律写出tan∠BA7C=,则n=( )
A.40
B.41
C.42
D.43
二.填空题
11.计算:cos60°tan30°+cot60°=
.
12.如图,△ABC中,∠C=90°,∠A=30°,BC=0.5cm,则AB的长是
cm.
13.在平面直角坐标系xOy中有一点A(3,4),如果OA与x轴正半轴的夹角为α,那么sinα=
.
14.在Rt△ABC中,∠C=90°,已知tanB=,则cosA=
.
15.比较sin80°与tan46°的大小,其中值较大的是
.
16.如图,点P、A、B、C在同一平面内,点A、B、C在同一直线上,且PC⊥AC,在点A处测得点P在北偏东60°方向上,在点B处测得点P在北偏东30°方向上,若AP=12千米,则A,B两点的距离为
千米.
17.如图,在Rt△ABC中,∠B=90°,∠ACD=130°,则∠A=
°.
18.一辆汽车沿倾斜角30°的斜坡前进100米,则它上升的高度是
米.
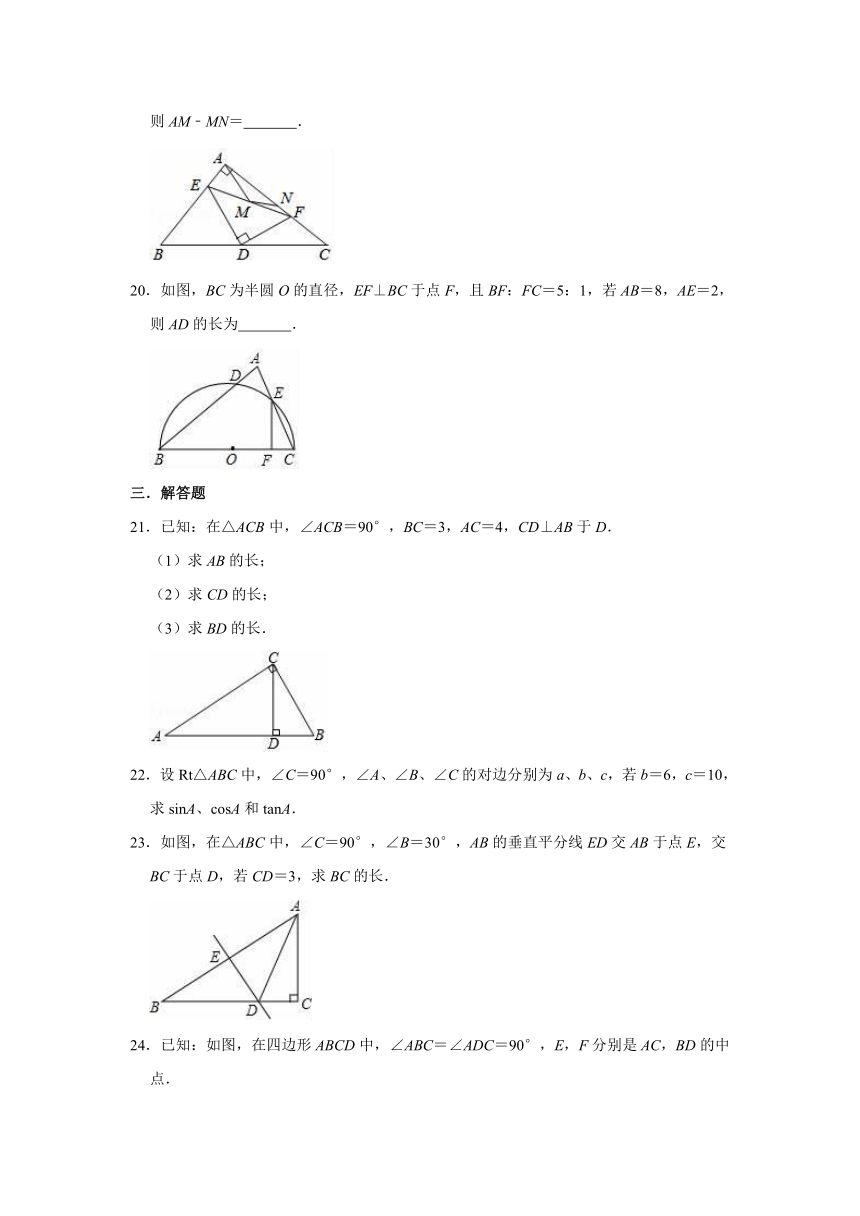
19.如图,在△ABC中,∠BAC=90°,点D是BC的中点,点E、F分别是AB、AC上的动点,∠EDF=90°,M、N分别是EF、AC的中点,连结AM、MN,若AC=6,AB=5,则AM﹣MN=
.
20.如图,BC为半圆O的直径,EF⊥BC于点F,且BF:FC=5:1,若AB=8,AE=2,则AD的长为
.
三.解答题
21.已知:在△ACB中,∠ACB=90°,BC=3,AC=4,CD⊥AB于D.
(1)求AB的长;
(2)求CD的长;
(3)求BD的长.
22.设Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,若b=6,c=10,求sinA、cosA和tanA.
23.如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线ED交AB于点E,交BC于点D,若CD=3,求BC的长.
24.已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,E,F分别是AC,BD的中点.
求证:EF⊥BD.
25.计算:
(1)2sin30°+3cos60°﹣4tan45°
(2)+tan260°
26.如图,某商场门前的台阶高出地面0.8米,即CB=0.8米,现将此台阶改造成供轮椅行走的斜坡AC,并且设计斜坡的倾斜角∠A为10°.求斜坡AC的长.(结果精确到0.1m)
【参考数据:sin10°=0.17.cos10°=0.98,tan10°=0.18】
27.如图,某天然气公司的主输气管道途经A小区,继续沿A小区的北偏东60°方向往前铺设,测绘员在A处测得另一个需要安装天然气的M小区位于北偏东30°方向,测绘员从A处出发,沿主输气管道步行到达C处,此时测得M小区位于北偏西60°方向.
(1)则AM与MC的位置关系为
;∠ACM=
度.
(2)现要在主输气管道AC上选择一个支管道连接点N,使从N处到M小区铺设的管道最短,且AC=4000米,求A小区与支管道连接点N的距离.
参考答案与试题解析
一.选择题
1.解:∵∠BCD=90°,点E是BD的中点,
∴CE=BE=DE,
∵AB⊥BD,
∴∠ABE=90°,
∴AE>BE,
∴AE>CE.
故选:B.
2.解:原式=+
=.
故选:C.
3.解:使用计算器计算得,
4sin60°≈3.464101615,
故选:B.
4.解:∵CD是斜边AB边上的高,
∴CD2=AD?BD=24×6=144,
∴CD=12.
故选:C.
5.解:在Rt△ABC中,∠A=90°,sinB=,
则=,
解得,BC=6,
故选:C.
6.解:∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠ACD=90°,∠A+∠ACD=90°,
∴∠BCD=∠A=60°,
∴∠ACD=∠B=30°,
∵AD=2,
∴AC=2AD=4,
∴AB=2AC=8,
∴BD=AB﹣AD=8﹣2=6.
故选:C.
7.解:原式=sin210°+cos210°+sin220°+cos220°
=1+1
=2.
故选:B.
8.解:如图,过点D作DE⊥OC于点E,
则点D到OB的距离等于OE的长.
∵四边形ABCD是矩形,
∴∠BCD=90°,CD=AB=a,AD=BC=b,
∴∠CDE=∠BCO=x,
∴OC=BC?cosx=bcosx,
CE=CD?sinx=asinx,
∴OE=OC+CE=bcosx+asinx.
则点D到OB的距离等于bcosx+asinx.
故选:C.
9.解:①由∠A+∠B+∠C=180°,∠A=∠B﹣∠C得到:2∠B=180°,则∠B=90°,则△ABC是直角三角形,故符合题意;
②∠A﹣∠B=90°得到:∠A>90°,则△ABC不是直角三角形,故不符合题意;
③由∠A+∠B+∠C=180°,∠A=∠B=2∠C得到:5∠C=180°,则∠C=36°,则∠A=∠B=72°<90°,则△ABC不是直角三角形,故不符合题意;
④由∠A+∠B+∠C=180°,∠A=∠B=∠C得到:∠C=90°,则△ABC是直角三角形,故符合题意;
综上所述,是直角三角形的是①④,共2个.
故选:B.
10.解:作CH⊥BA4于H,
由勾股定理得,BA4==,A4C=,
△BA4C的面积=4﹣2﹣=,
∴CH=,
解得,CH=,
则A4H==,
∴tan∠BA4C==,
1=12﹣1+1,
3=22﹣2+1,
7=32﹣3+1,
∴tan∠BAnC=,
∴tan∠BA7C=,
则n=43.
故选:D.
二.填空题
11.解:原式=×+
=+
=.
故答案为:.
12.解:∵△ABC中,∠C=90°,∠A=30°,BC=0.5cm,
∴AB=2BC=1cm.
故答案为:3.
13.解:∵A(3,4),
∴OA==5,
∴sinα=.
故答案为:.
14.解:如图:
设AC=x,
∵tanB=,
∴BC=2x,
∴AB==x,
∴cosA===.
故答案为:.
15.解:∵sinα随α的增大而增大,且sin80°<sin90°,
∴sin80°<1,
∵tanα随α的增大而增大,且tan46°>tan45°,
∴tan46°>1,
则tan46°>sin80°,
故答案为:tan46°.
16.解:∵PC⊥AC,在点A处测得点P在北偏东60°方向上,
∴∠PCA=90°,∠PAC=30°,
∵AP=12千米,
∴PC=6千米,AC=6千米,
∵在点B处测得点P在北偏东30°方向上,∠PCB=90°,PC=6千米,
∴∠PBC=60°,
∴BC===2千米,
∴AB=AC﹣BC=6﹣2=4(千米),
故答案为:4千米.
17.解:∵∠ACD的△ABC的一个外角,
∴∠A=∠ACD﹣∠B=130°﹣90°=40°,
故答案为:40.
18.解:如图所示:
由题意得:∠ACB=90°,∠A=30°,AB=100,
∴BC=AB=50(米).
故答案为:50.
19.解:如图,连接DM,DN,
∵∠BAC=∠EDF=90°,
∵M是EF的中点,
∴AM=DM=EF,
∴AM﹣MN=DM﹣MN≤DN(当D,M,N共线时,等号成立),
∵D、N分别是BC、AC的中点,即DN是△ABC的中位线,
∴DN=AB=.
故答案为:.
20.解:连接BE.
∵BC是直径.
∴∠AEB=∠BEC=90°
在直角△ABE中,根据勾股定理可得:BE2=AB2﹣AE2=82﹣22=60.
∵=5
∴设FC=x,则BF=5x,BC=6x.
又∵BE2=BF?BC
即:30x2=60
解得:x=,
∴EC2=FC?BC=6x2=12
∴EC=2,
∴AC=AE+EC=2+2,
∵AD?AB=AE?AC
∴AD===.
故答案为.
三.解答题
21.解:(1)∵∠ACB=90°,BC=3,AC=4,
∴AB==5;
(2)∵CD⊥AB,
∴CD?AB=AC?BC,
∴CD==;
(3)∵BC2=BD?BA,
∴BD==.
22.解:如图所示:∵Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,b=6,c=10,
∴a==8,
∴sinA===;
cosA===;
tanA===.
23.解:∵DE是线段AB的垂直平分线,
∴AD=BD,
∵∠B=30°,
∴∠BAD=∠B=30°,
又∵∠C=90°,
∴∠CAB=90°﹣∠B=90°﹣30°=60°,
∴∠DAC=∠CAB﹣∠BAD=60°﹣30°=30°,
在Rt△ACD中,CD=AD,
∴AD=2CD=2×3=6,
∴BD=AD=6,
∴BC=BD+CD=6+3=9.
24.证明:连接BE、DE,
∵∠ABC=∠ADC=90°,E是AC的中点,
∴EB=ED=AC,
∴△BED是等腰三角形,
∵F是BD的中点,
∴EF是BD中线,
∴EF⊥DB.
25.解:(1)原式=
=
=;
(2)原式=
=+3
=.
26.解:在Rt△ABC中,sinA=,
∴AC===≈4.7(m),
答:斜坡AC的长约为4.7m.
27.解:(1)∵∠MAC=60°﹣30°=30°,∠ACM=30°+30°=60°,
∴∠AMC=180°﹣30°﹣60°=90°,
故答案为:垂直,60;
(2)当MN⊥AC时,从N到M小区铺设的管道最短,
在Rt△AMC中,∵∠AMC=90°,∠MAC=30°,AC=4000,
∴AM=AC?cos∠MAC=4000×=2000(米),
在Rt△AMN中,∵∠ANM=90°,cos30°=,
∴AN=AM?cos30°=2000×=3000(米).
答:AN的长为3000米.
解直角三角形》单元测试卷
一.选择题
1.如图所示,在四边形ABCD中,∠BCD=90°,AB⊥BD于点B,点E是BD的中点,连接AE,CE,则AE与CE的大小关系是( )
A.AE=CE
B.AE>CE
C.AE<CE
D.AE=2CE
2.sin45°+cos45°的值为( )
A.1
B.2
C.
D.2
3.某款国产手机上有科学计算器,依次按键:,显示的结果在哪两个相邻整数之间( )
A.2~3
B.3~4
C.4~5
D.5~6
4.如图,∠ACB=90°,CD是AB边上的高,若AD=24,BD=6,则CD的长是( )
A.8
B.10
C.12
D.14
5.如图,在Rt△ABC中,∠A=90°,sinB=,AC=2,则BC长为( )
A.2
B.4
C.6
D.8
6.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,AD=2,则BD=( )
A.2
B.4
C.6
D.8
7.式子sin210°+sin220°+cos210°+cos220°的值为( )
A.1
B.2
C.3
D.4
8.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点D到OB的距离等于( )
A.asinx+bsinx
B.acosx+bcosx
C.asinx+bcosx
D.acosx+bsinx
9.在下列条件中:①∠A=∠B﹣∠C,②∠A﹣∠B=90°,③∠A=∠B=2∠C,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A.1个
B.2个
C.3个
D.4个
10.如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=,tan∠BA3C=…,依此规律写出tan∠BA7C=,则n=( )
A.40
B.41
C.42
D.43
二.填空题
11.计算:cos60°tan30°+cot60°=
.
12.如图,△ABC中,∠C=90°,∠A=30°,BC=0.5cm,则AB的长是
cm.
13.在平面直角坐标系xOy中有一点A(3,4),如果OA与x轴正半轴的夹角为α,那么sinα=
.
14.在Rt△ABC中,∠C=90°,已知tanB=,则cosA=
.
15.比较sin80°与tan46°的大小,其中值较大的是
.
16.如图,点P、A、B、C在同一平面内,点A、B、C在同一直线上,且PC⊥AC,在点A处测得点P在北偏东60°方向上,在点B处测得点P在北偏东30°方向上,若AP=12千米,则A,B两点的距离为
千米.
17.如图,在Rt△ABC中,∠B=90°,∠ACD=130°,则∠A=
°.
18.一辆汽车沿倾斜角30°的斜坡前进100米,则它上升的高度是
米.
19.如图,在△ABC中,∠BAC=90°,点D是BC的中点,点E、F分别是AB、AC上的动点,∠EDF=90°,M、N分别是EF、AC的中点,连结AM、MN,若AC=6,AB=5,则AM﹣MN=
.
20.如图,BC为半圆O的直径,EF⊥BC于点F,且BF:FC=5:1,若AB=8,AE=2,则AD的长为
.
三.解答题
21.已知:在△ACB中,∠ACB=90°,BC=3,AC=4,CD⊥AB于D.
(1)求AB的长;
(2)求CD的长;
(3)求BD的长.
22.设Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,若b=6,c=10,求sinA、cosA和tanA.
23.如图,在△ABC中,∠C=90°,∠B=30°,AB的垂直平分线ED交AB于点E,交BC于点D,若CD=3,求BC的长.
24.已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,E,F分别是AC,BD的中点.
求证:EF⊥BD.
25.计算:
(1)2sin30°+3cos60°﹣4tan45°
(2)+tan260°
26.如图,某商场门前的台阶高出地面0.8米,即CB=0.8米,现将此台阶改造成供轮椅行走的斜坡AC,并且设计斜坡的倾斜角∠A为10°.求斜坡AC的长.(结果精确到0.1m)
【参考数据:sin10°=0.17.cos10°=0.98,tan10°=0.18】
27.如图,某天然气公司的主输气管道途经A小区,继续沿A小区的北偏东60°方向往前铺设,测绘员在A处测得另一个需要安装天然气的M小区位于北偏东30°方向,测绘员从A处出发,沿主输气管道步行到达C处,此时测得M小区位于北偏西60°方向.
(1)则AM与MC的位置关系为
;∠ACM=
度.
(2)现要在主输气管道AC上选择一个支管道连接点N,使从N处到M小区铺设的管道最短,且AC=4000米,求A小区与支管道连接点N的距离.
参考答案与试题解析
一.选择题
1.解:∵∠BCD=90°,点E是BD的中点,
∴CE=BE=DE,
∵AB⊥BD,
∴∠ABE=90°,
∴AE>BE,
∴AE>CE.
故选:B.
2.解:原式=+
=.
故选:C.
3.解:使用计算器计算得,
4sin60°≈3.464101615,
故选:B.
4.解:∵CD是斜边AB边上的高,
∴CD2=AD?BD=24×6=144,
∴CD=12.
故选:C.
5.解:在Rt△ABC中,∠A=90°,sinB=,
则=,
解得,BC=6,
故选:C.
6.解:∵∠ACB=90°,CD⊥AB,
∴∠BCD+∠ACD=90°,∠A+∠ACD=90°,
∴∠BCD=∠A=60°,
∴∠ACD=∠B=30°,
∵AD=2,
∴AC=2AD=4,
∴AB=2AC=8,
∴BD=AB﹣AD=8﹣2=6.
故选:C.
7.解:原式=sin210°+cos210°+sin220°+cos220°
=1+1
=2.
故选:B.
8.解:如图,过点D作DE⊥OC于点E,
则点D到OB的距离等于OE的长.
∵四边形ABCD是矩形,
∴∠BCD=90°,CD=AB=a,AD=BC=b,
∴∠CDE=∠BCO=x,
∴OC=BC?cosx=bcosx,
CE=CD?sinx=asinx,
∴OE=OC+CE=bcosx+asinx.
则点D到OB的距离等于bcosx+asinx.
故选:C.
9.解:①由∠A+∠B+∠C=180°,∠A=∠B﹣∠C得到:2∠B=180°,则∠B=90°,则△ABC是直角三角形,故符合题意;
②∠A﹣∠B=90°得到:∠A>90°,则△ABC不是直角三角形,故不符合题意;
③由∠A+∠B+∠C=180°,∠A=∠B=2∠C得到:5∠C=180°,则∠C=36°,则∠A=∠B=72°<90°,则△ABC不是直角三角形,故不符合题意;
④由∠A+∠B+∠C=180°,∠A=∠B=∠C得到:∠C=90°,则△ABC是直角三角形,故符合题意;
综上所述,是直角三角形的是①④,共2个.
故选:B.
10.解:作CH⊥BA4于H,
由勾股定理得,BA4==,A4C=,
△BA4C的面积=4﹣2﹣=,
∴CH=,
解得,CH=,
则A4H==,
∴tan∠BA4C==,
1=12﹣1+1,
3=22﹣2+1,
7=32﹣3+1,
∴tan∠BAnC=,
∴tan∠BA7C=,
则n=43.
故选:D.
二.填空题
11.解:原式=×+
=+
=.
故答案为:.
12.解:∵△ABC中,∠C=90°,∠A=30°,BC=0.5cm,
∴AB=2BC=1cm.
故答案为:3.
13.解:∵A(3,4),
∴OA==5,
∴sinα=.
故答案为:.
14.解:如图:
设AC=x,
∵tanB=,
∴BC=2x,
∴AB==x,
∴cosA===.
故答案为:.
15.解:∵sinα随α的增大而增大,且sin80°<sin90°,
∴sin80°<1,
∵tanα随α的增大而增大,且tan46°>tan45°,
∴tan46°>1,
则tan46°>sin80°,
故答案为:tan46°.
16.解:∵PC⊥AC,在点A处测得点P在北偏东60°方向上,
∴∠PCA=90°,∠PAC=30°,
∵AP=12千米,
∴PC=6千米,AC=6千米,
∵在点B处测得点P在北偏东30°方向上,∠PCB=90°,PC=6千米,
∴∠PBC=60°,
∴BC===2千米,
∴AB=AC﹣BC=6﹣2=4(千米),
故答案为:4千米.
17.解:∵∠ACD的△ABC的一个外角,
∴∠A=∠ACD﹣∠B=130°﹣90°=40°,
故答案为:40.
18.解:如图所示:
由题意得:∠ACB=90°,∠A=30°,AB=100,
∴BC=AB=50(米).
故答案为:50.
19.解:如图,连接DM,DN,
∵∠BAC=∠EDF=90°,
∵M是EF的中点,
∴AM=DM=EF,
∴AM﹣MN=DM﹣MN≤DN(当D,M,N共线时,等号成立),
∵D、N分别是BC、AC的中点,即DN是△ABC的中位线,
∴DN=AB=.
故答案为:.
20.解:连接BE.
∵BC是直径.
∴∠AEB=∠BEC=90°
在直角△ABE中,根据勾股定理可得:BE2=AB2﹣AE2=82﹣22=60.
∵=5
∴设FC=x,则BF=5x,BC=6x.
又∵BE2=BF?BC
即:30x2=60
解得:x=,
∴EC2=FC?BC=6x2=12
∴EC=2,
∴AC=AE+EC=2+2,
∵AD?AB=AE?AC
∴AD===.
故答案为.
三.解答题
21.解:(1)∵∠ACB=90°,BC=3,AC=4,
∴AB==5;
(2)∵CD⊥AB,
∴CD?AB=AC?BC,
∴CD==;
(3)∵BC2=BD?BA,
∴BD==.
22.解:如图所示:∵Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,b=6,c=10,
∴a==8,
∴sinA===;
cosA===;
tanA===.
23.解:∵DE是线段AB的垂直平分线,
∴AD=BD,
∵∠B=30°,
∴∠BAD=∠B=30°,
又∵∠C=90°,
∴∠CAB=90°﹣∠B=90°﹣30°=60°,
∴∠DAC=∠CAB﹣∠BAD=60°﹣30°=30°,
在Rt△ACD中,CD=AD,
∴AD=2CD=2×3=6,
∴BD=AD=6,
∴BC=BD+CD=6+3=9.
24.证明:连接BE、DE,
∵∠ABC=∠ADC=90°,E是AC的中点,
∴EB=ED=AC,
∴△BED是等腰三角形,
∵F是BD的中点,
∴EF是BD中线,
∴EF⊥DB.
25.解:(1)原式=
=
=;
(2)原式=
=+3
=.
26.解:在Rt△ABC中,sinA=,
∴AC===≈4.7(m),
答:斜坡AC的长约为4.7m.
27.解:(1)∵∠MAC=60°﹣30°=30°,∠ACM=30°+30°=60°,
∴∠AMC=180°﹣30°﹣60°=90°,
故答案为:垂直,60;
(2)当MN⊥AC时,从N到M小区铺设的管道最短,
在Rt△AMC中,∵∠AMC=90°,∠MAC=30°,AC=4000,
∴AM=AC?cos∠MAC=4000×=2000(米),
在Rt△AMN中,∵∠ANM=90°,cos30°=,
∴AN=AM?cos30°=2000×=3000(米).
答:AN的长为3000米.
