30.2反比例函数的图象和性质(2)

(共8张PPT)
0
y
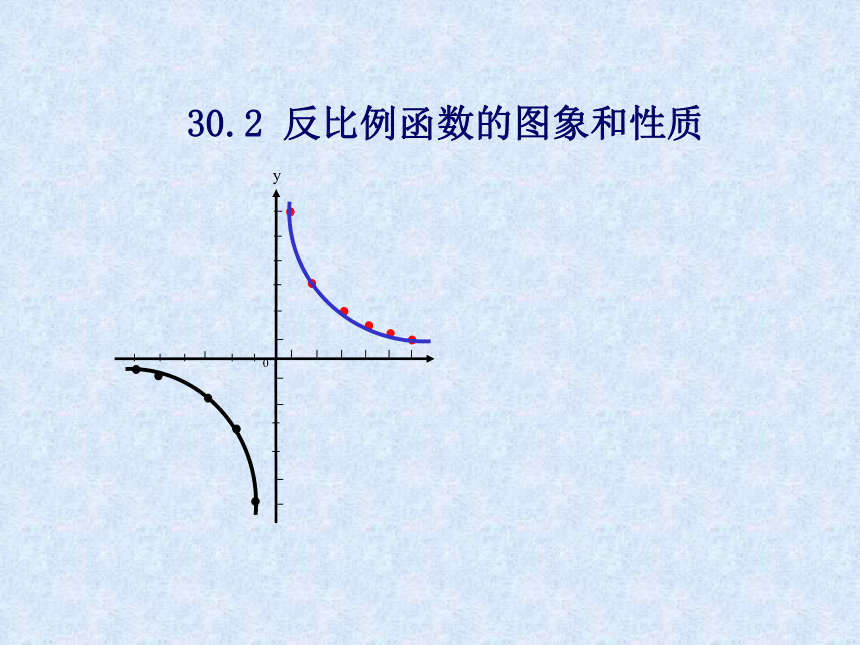
30.2 反比例函数的图象和性质
y
x
0
1
2
3
4
5
6
1
2
3
4
5
6
图象？
1
3
4
6
5
2
6
1.5
1
1.2
3
2
x
y
...
...
… -6 -5 -4 -3 -2 -1
... -1 -1.2 -1.5 -2 -3 -6
列表
描点
连线
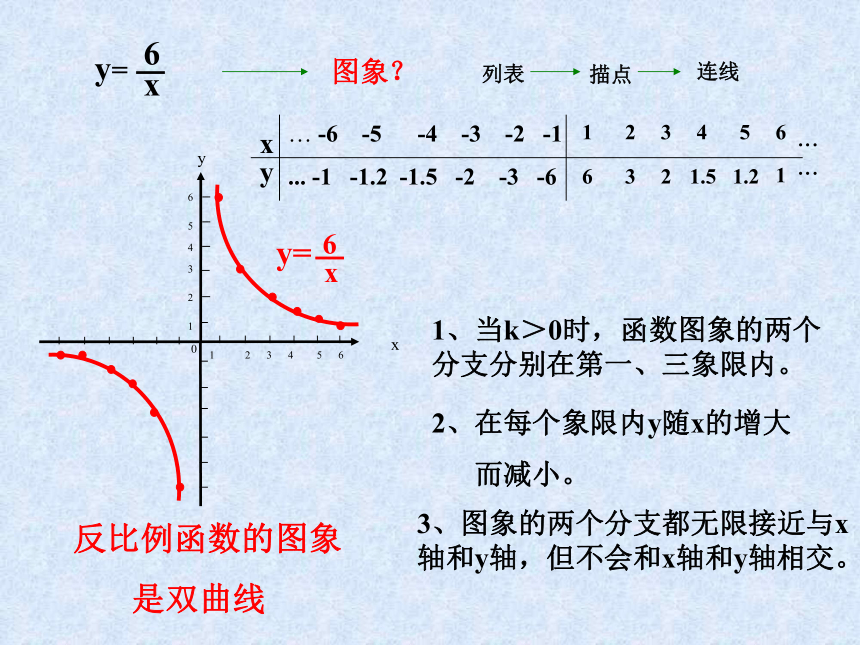
反比例函数的图象
是双曲线
1、当k＞0时，函数图象的两个分支分别在第一、三象限内。
2、在每个象限内y随x的增大
而减小。
3、图象的两个分支都无限接近与x轴和y轴，但不会和x轴和y轴相交。
y=
6
x
y=
6
x
...
...
4
6
-6
1
2
3
5
-3
-2
-1.5
- 1.2
-1
y
x
-4
-6
2
-1
-2
-3
-5
3
1.2
1
6
1.5
...
...
y=
6
x
y=
6
x
-4
0
-5
1
-3
y
x
2
3
4
5
-1
6
-2
-6
1
1、当k＜0时，函数图象的两个分支分别在第二、四象限内。
2、在每个象限内y随x的增大而增大。
3、图象的两个分支都无限接近与x轴和y轴，但不会和x轴和y轴相交。
图象？
y=
6
x
练一练：
反比例函数y=- 的图象是 ，分布
在第 象限，在每个象限内， y都随x的
增大而 ；若 p1 (x1 , y1)、p2 (x2 , y2) 都在第
二象限且x12
x
双曲 线
二、四
增大
例1：已知反比例函数y=mxm -5 ，它的两个分支分别在第一、第三象限，求m的值？
得 m =2
解：因为反比例函数y=mxm -5 ，它
的
两个分支分别在第一、第三象限
m﹥0
m -5= -1
所以必须满足｛
y=mxm -5
x
y
o
例2、根据下图中点的坐标
（1）求出y与x的函数解析式。
（2）如果点A（-2，b）
在双曲线上，求b的值。
A(-2,b)
(3,-1)
y
x
0
(3)比较绿色部分和黄色部分的面积的大小。
答：一样大。因为双曲线上任何一点的横坐标与纵坐标的乘积是一个常数。
.
B
如图：A、B是双曲线y= 上的
任意两点 。 过A、B两点分别作
x轴和y轴的垂线，试确定图中两
个三角形的面积各是多少？
5
x
x
y
o
A
y=
5
x
B
答：面积都是 。
5
2
想一想
反比例函数y= 上有两点A（x1，y1）和
B（x2，y2）。
若x1 ＜ x2 ＜0 ，则 y1-------y2；
若 x1 > x2 > 0 , 则 y1 ----- y2 ;
若 x1 > 0 , x2 ＜0, 则 y1-----y2 .
6
x
试一试