抛物线的定义及标准方程
图片预览



文档简介
(共18张PPT)
2.4.1抛物线的
定义及标准方程
*
京山县第一高级中学
·
M
F
l
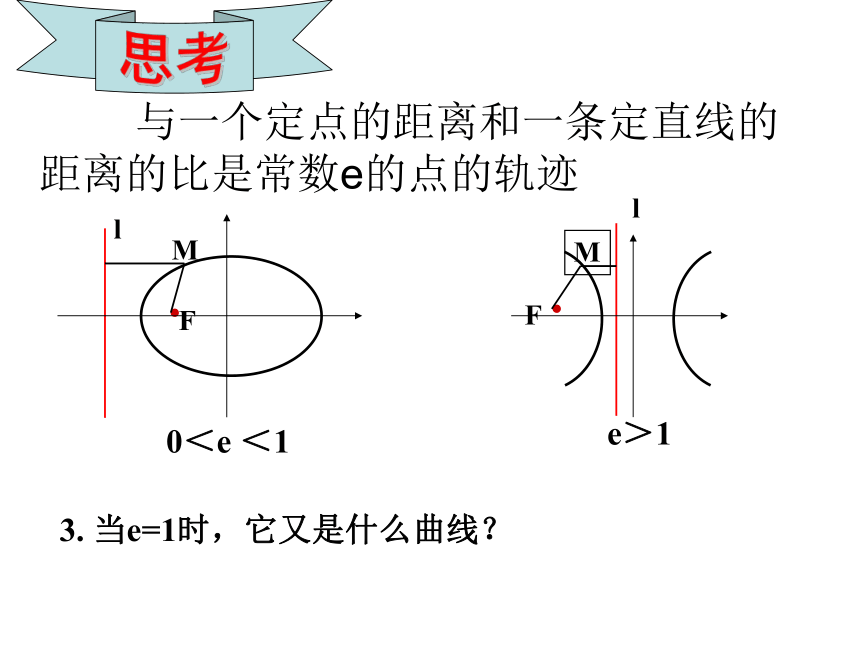
0<e <1
l
F
·
M
e>1
3. 当e=1时,它又是什么曲线?
与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹
·
·
F
M
ι
N
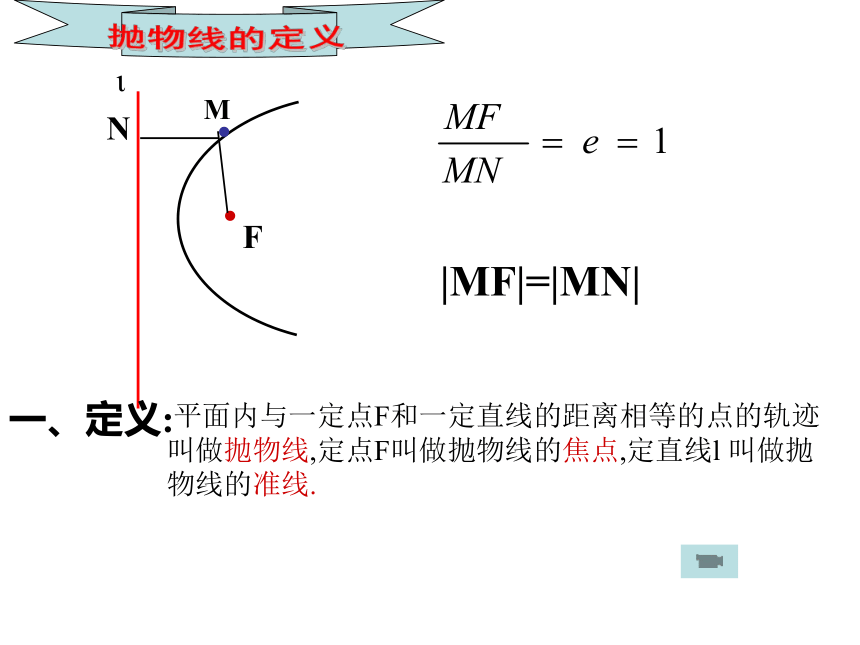
|MF|=|MN|
平面内与一定点F和一定直线的距离相等的点的轨迹叫做抛物线,定点F叫做抛物线的焦点,定直线l 叫做抛物线的准线.
一、定义:
·
·
F
M
l
N
·
·
F
M
l
N
·
·
F
M
l
N
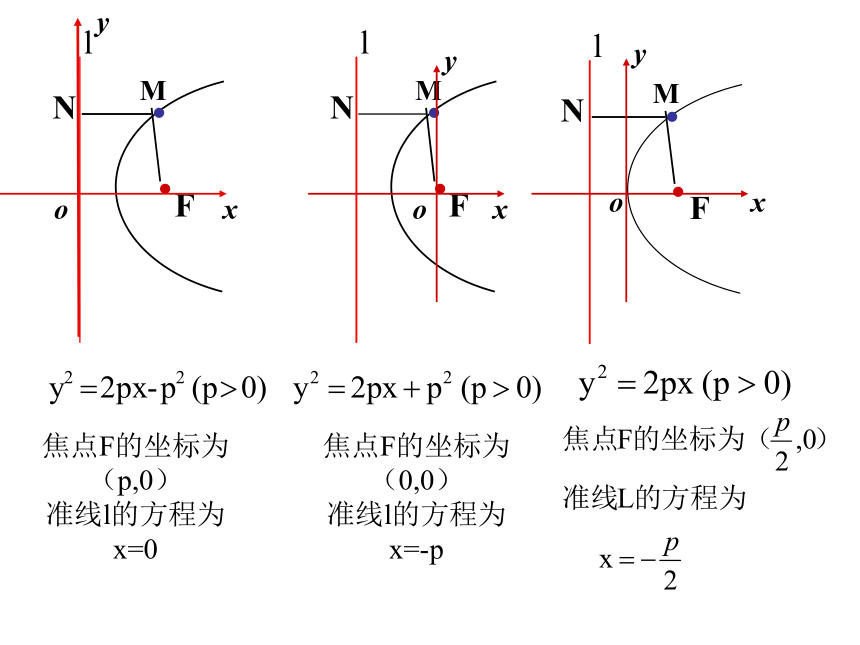
焦点F的坐标为(p,0)
准线l的方程为x=0
焦点F的坐标为(0,0)
准线l的方程为x=-p
x
y
o
x
y
o
x
y
o
x
y
o
·
·
F
M
l
N
K
则F( ,0),l:x = -
p
2
p
2
设点M的坐标为(x,y),
化简得 y2 = 2px(p>0)
2
由定义得:
(焦点在x轴正半轴上,坐标(p/2,0),准线方程x=-p/2.)
P 为焦 点 到 准 线 的 距 离
建立直角坐标系xoy,使x轴经过焦点F且垂直于直线l,垂
足为K,并使原点与线段KF中点重合。
设︱KF︱= p
(p > 0),
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
图 形 焦 点 准 线 标准方程
例1:(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
(2)已知抛物线的焦点是 F(0,-2),求它的标
准方程.
解:因为p=3,所以焦点坐标是 (3/2,0),准线方程
是 x = -3/2.
解:因为焦点在y轴的负半轴上,并且p/2=2,p=4,
所以所求抛物线的标准方程是x2 =-8y
解析
1、根据下列条件写出抛物线的标准方程:
(1)焦点是F(3,0);
(2)准线方程是x=- ;
(3)焦点到准线的距离是2;
y2=12x
y2=x
y2=4x , y2=-4x , x2=4y , x2=-4y
2、求下列抛物线的焦点坐标和准线方程:
F(0 , -2) , y=2 ;
F(5,0),x=-5
(A) y2 = - 4x
1 . 选择题:
(1) 准线方程为x=2的抛物线的标准方程是( )
(B) y2 = - 8x
(D) y2 = 8x
(C) y2 = 4x
(2) 抛物线x2 +y=0 的焦点位于 ( )
(A) x轴的负半轴上
(B) x轴的正半轴上
(D) y轴的正半轴上
(C) y轴的负半轴上
B
C
2 . 填空题:
(1) 焦点在直线3x-4y-12=0上的抛物线
的标准方程为
经过点(-8,8)的抛物线的标准方程为
y2 = 16x 或 x2 = -12x
y2 = -8x 或 x2 = 8y
1 . 抛物线的定义 :
平面内与一个定点F和一条定直线L的
距离相等的点的轨迹叫做 抛物线 .点F叫
做抛物线的焦点,直线L叫做抛物线的准线.
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
图 形 焦 点 准 线 标准方程
2.4.1抛物线的
定义及标准方程
*
京山县第一高级中学
·
M
F
l
0<e <1
l
F
·
M
e>1
3. 当e=1时,它又是什么曲线?
与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹
·
·
F
M
ι
N
|MF|=|MN|
平面内与一定点F和一定直线的距离相等的点的轨迹叫做抛物线,定点F叫做抛物线的焦点,定直线l 叫做抛物线的准线.
一、定义:
·
·
F
M
l
N
·
·
F
M
l
N
·
·
F
M
l
N
焦点F的坐标为(p,0)
准线l的方程为x=0
焦点F的坐标为(0,0)
准线l的方程为x=-p
x
y
o
x
y
o
x
y
o
x
y
o
·
·
F
M
l
N
K
则F( ,0),l:x = -
p
2
p
2
设点M的坐标为(x,y),
化简得 y2 = 2px(p>0)
2
由定义得:
(焦点在x轴正半轴上,坐标(p/2,0),准线方程x=-p/2.)
P 为焦 点 到 准 线 的 距 离
建立直角坐标系xoy,使x轴经过焦点F且垂直于直线l,垂
足为K,并使原点与线段KF中点重合。
设︱KF︱= p
(p > 0),
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
图 形 焦 点 准 线 标准方程
例1:(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
(2)已知抛物线的焦点是 F(0,-2),求它的标
准方程.
解:因为p=3,所以焦点坐标是 (3/2,0),准线方程
是 x = -3/2.
解:因为焦点在y轴的负半轴上,并且p/2=2,p=4,
所以所求抛物线的标准方程是x2 =-8y
解析
1、根据下列条件写出抛物线的标准方程:
(1)焦点是F(3,0);
(2)准线方程是x=- ;
(3)焦点到准线的距离是2;
y2=12x
y2=x
y2=4x , y2=-4x , x2=4y , x2=-4y
2、求下列抛物线的焦点坐标和准线方程:
F(0 , -2) , y=2 ;
F(5,0),x=-5
(A) y2 = - 4x
1 . 选择题:
(1) 准线方程为x=2的抛物线的标准方程是( )
(B) y2 = - 8x
(D) y2 = 8x
(C) y2 = 4x
(2) 抛物线x2 +y=0 的焦点位于 ( )
(A) x轴的负半轴上
(B) x轴的正半轴上
(D) y轴的正半轴上
(C) y轴的负半轴上
B
C
2 . 填空题:
(1) 焦点在直线3x-4y-12=0上的抛物线
的标准方程为
经过点(-8,8)的抛物线的标准方程为
y2 = 16x 或 x2 = -12x
y2 = -8x 或 x2 = 8y
1 . 抛物线的定义 :
平面内与一个定点F和一条定直线L的
距离相等的点的轨迹叫做 抛物线 .点F叫
做抛物线的焦点,直线L叫做抛物线的准线.
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
图 形 焦 点 准 线 标准方程
