微专题八 证明两条线段相等的基本思路归纳(含答案)
文档属性
| 名称 | 微专题八 证明两条线段相等的基本思路归纳(含答案) | 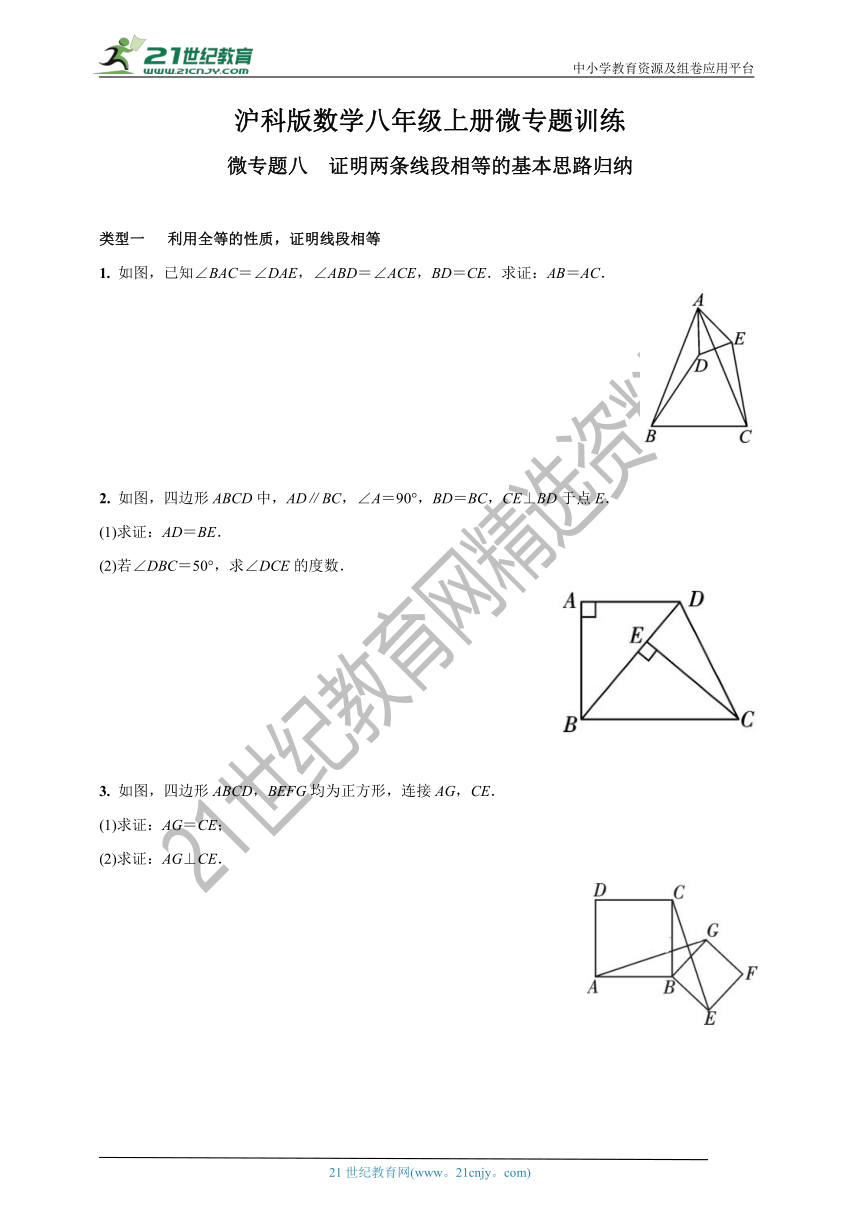 | |
| 格式 | doc | ||
| 文件大小 | 264.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 20:43:01 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
沪科版数学八年级上册微专题训练
微专题八 证明两条线段相等的基本思路归纳
类型一 利用全等的性质,证明线段相等
1. 如图,已知∠BAC=∠DAE,∠ABD=∠ACE,BD=CE.求证:AB=AC.
2. 如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,CE⊥BD于点E.
(1)求证:AD=BE.
(2)若∠DBC=50°,求∠DCE的度数.
3. 如图,四边形ABCD,BEFG均为正方形,连接AG,CE.
(1)求证:AG=CE;
(2)求证:AG⊥CE.
类型二 利用等腰三角形的性质与判定证明线段相等
4. 如图,已知△ABC中,过点C作∠BAC的平分线AD的垂线,垂足为D,作DE∥AB交AC于E,求证:AE=CE.
5. 如图,在△ABC中,AB=AC,∠A=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长交BC的延长线于点F.求证:AB=CF.
6. 如图,已知在等边三角形ABC的AC边上取中点D,在BC的延长上取一点E.使CE=CD.求证:BD=DE.
类型三 利用线段垂直平分线的性质,角平分线的性质证明线段相等
7. 如图,在Rt△ABC中,∠BAC=90°,AG⊥BC于点G,BD平分∠ABC,AE⊥BD于点H,交BC于点E,AG与BD相交于点F,求证:EF=AD.
8. 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)AD=FC;
(2)AB=BC+AD.
参考答案
1. 证明:∵∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.在△ABD和△ACE中, ∴△ABD≌△ACE(AAS),∴AB=AC.
2. (1)证明:∵AD∥BC,∴∠ADB=∠DBC.又∵CE⊥BD,∴∠BEC=90°.∵∠A=90°,∴∠A=∠BEC.又∵BD=BC,∴△ABD≌△ECB(AAS),∴AD=EB.
(2)解:∵BD=BC,∠DBC=50°,∴∠EDC=∠DCB=65°.又∵CE⊥BD,∴∠CED=90°,∴∠DCE=90°-∠EDC=25°.
3. 证明:(1)∵四边形ABCD,BEFG均为正方形,∴AB=CB,∠ABC=∠GBE=90°,BG=BE,∴∠ABG=∠CBE.在△ABG和△CBE中, ∴△ABG≌△CBE(SAS),∴AG=CE;
(2)设AG与BC交于点M,CE与BG交于点N,由(1)可知△ABG≌△CBE,∴∠BAG=∠BCE,∵∠ABC=90°,∴∠BAG+∠AMB=90°.∵∠AMB=∠CMN,∴∠BCE+∠CMN=90°,∴∠CNM=90°,∴AG⊥CE.
4. 证明:∵AD是∠BAC的平分线,∴∠BAD=∠DAC,∵DE∥AB,∴∠ADE=∠BAD,∴∠EAD=∠EDA,∴AE=DE.∵AD⊥CD,∴∠CAD+∠ACD=90°,∴∠ADE+∠EDC=90°,∵∠EDA=∠EAD,∴∠EDC=∠ACD,∴DE=CE,∴AE=CE.
5. 证明:连接AF.∵AB=AC,∠BAC=36°,∴∠ABC=∠ACB=72°.∵BD平分∠ABC,∴∠ABD=∠DBF=36°,∴∠ABD=∠BAD=36°,∴DA=DB.∵AE=BE,∴EF⊥AB,即FE是AB的垂直平分线,∴FA=FB,∴∠FAB=∠ABC=72°,∴∠FAC=∠FAB-∠BAC=36°,∵∠ACB=∠FAC+∠AFC,∴∠AFC=∠ACB-∠FAC=36°.∴∠FAC=∠AFC,∴AC=CF,∴AB=CF.
6. 证明:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°.∵D为AC中点,∴∠DBC=30°,∵CE=CD,∠E=∠CDE=∠ACB=30°,∴∠DBC=∠E,∴BD=DE.
7. 证明:∵BD平分∠ABC,AE⊥BD,∴BH为AE的垂直平分线,∵F在BD上,∴AF=EF.∵BD平分∠ABC,∴∠DBC=∠ABD,∵∠BAC=90°,AG⊥BC,∴∠ABD+∠ADB=90°,∠DBC+∠BFG=90°,∴∠ADB=∠BFG,∵∠AFD=∠BFG,∴∠ADB=∠AFD,∴AF=AD,又∵AF=EF,∴AD=EF.
8. 证明:(1)∵AD∥BC,∴∠ADE=∠FCE,∵E是CD的中点,∴DE=EC.在△ADE和△FCE中, ∴△ADE≌△FCE(ASA),∴AD=FC;
(2)∵△ADE≌△FCE,∴AE=FE,AD=FC.又∵BE⊥AE,∴BE是线段AF的垂直平分线,∴AB=BF=BC+CF=BC+AD.
_21?????????è?????(www???21cnjy???com)_
沪科版数学八年级上册微专题训练
微专题八 证明两条线段相等的基本思路归纳
类型一 利用全等的性质,证明线段相等
1. 如图,已知∠BAC=∠DAE,∠ABD=∠ACE,BD=CE.求证:AB=AC.
2. 如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,CE⊥BD于点E.
(1)求证:AD=BE.
(2)若∠DBC=50°,求∠DCE的度数.
3. 如图,四边形ABCD,BEFG均为正方形,连接AG,CE.
(1)求证:AG=CE;
(2)求证:AG⊥CE.
类型二 利用等腰三角形的性质与判定证明线段相等
4. 如图,已知△ABC中,过点C作∠BAC的平分线AD的垂线,垂足为D,作DE∥AB交AC于E,求证:AE=CE.
5. 如图,在△ABC中,AB=AC,∠A=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长交BC的延长线于点F.求证:AB=CF.
6. 如图,已知在等边三角形ABC的AC边上取中点D,在BC的延长上取一点E.使CE=CD.求证:BD=DE.
类型三 利用线段垂直平分线的性质,角平分线的性质证明线段相等
7. 如图,在Rt△ABC中,∠BAC=90°,AG⊥BC于点G,BD平分∠ABC,AE⊥BD于点H,交BC于点E,AG与BD相交于点F,求证:EF=AD.
8. 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)AD=FC;
(2)AB=BC+AD.
参考答案
1. 证明:∵∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.在△ABD和△ACE中, ∴△ABD≌△ACE(AAS),∴AB=AC.
2. (1)证明:∵AD∥BC,∴∠ADB=∠DBC.又∵CE⊥BD,∴∠BEC=90°.∵∠A=90°,∴∠A=∠BEC.又∵BD=BC,∴△ABD≌△ECB(AAS),∴AD=EB.
(2)解:∵BD=BC,∠DBC=50°,∴∠EDC=∠DCB=65°.又∵CE⊥BD,∴∠CED=90°,∴∠DCE=90°-∠EDC=25°.
3. 证明:(1)∵四边形ABCD,BEFG均为正方形,∴AB=CB,∠ABC=∠GBE=90°,BG=BE,∴∠ABG=∠CBE.在△ABG和△CBE中, ∴△ABG≌△CBE(SAS),∴AG=CE;
(2)设AG与BC交于点M,CE与BG交于点N,由(1)可知△ABG≌△CBE,∴∠BAG=∠BCE,∵∠ABC=90°,∴∠BAG+∠AMB=90°.∵∠AMB=∠CMN,∴∠BCE+∠CMN=90°,∴∠CNM=90°,∴AG⊥CE.
4. 证明:∵AD是∠BAC的平分线,∴∠BAD=∠DAC,∵DE∥AB,∴∠ADE=∠BAD,∴∠EAD=∠EDA,∴AE=DE.∵AD⊥CD,∴∠CAD+∠ACD=90°,∴∠ADE+∠EDC=90°,∵∠EDA=∠EAD,∴∠EDC=∠ACD,∴DE=CE,∴AE=CE.
5. 证明:连接AF.∵AB=AC,∠BAC=36°,∴∠ABC=∠ACB=72°.∵BD平分∠ABC,∴∠ABD=∠DBF=36°,∴∠ABD=∠BAD=36°,∴DA=DB.∵AE=BE,∴EF⊥AB,即FE是AB的垂直平分线,∴FA=FB,∴∠FAB=∠ABC=72°,∴∠FAC=∠FAB-∠BAC=36°,∵∠ACB=∠FAC+∠AFC,∴∠AFC=∠ACB-∠FAC=36°.∴∠FAC=∠AFC,∴AC=CF,∴AB=CF.
6. 证明:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°.∵D为AC中点,∴∠DBC=30°,∵CE=CD,∠E=∠CDE=∠ACB=30°,∴∠DBC=∠E,∴BD=DE.
7. 证明:∵BD平分∠ABC,AE⊥BD,∴BH为AE的垂直平分线,∵F在BD上,∴AF=EF.∵BD平分∠ABC,∴∠DBC=∠ABD,∵∠BAC=90°,AG⊥BC,∴∠ABD+∠ADB=90°,∠DBC+∠BFG=90°,∴∠ADB=∠BFG,∵∠AFD=∠BFG,∴∠ADB=∠AFD,∴AF=AD,又∵AF=EF,∴AD=EF.
8. 证明:(1)∵AD∥BC,∴∠ADE=∠FCE,∵E是CD的中点,∴DE=EC.在△ADE和△FCE中, ∴△ADE≌△FCE(ASA),∴AD=FC;
(2)∵△ADE≌△FCE,∴AE=FE,AD=FC.又∵BE⊥AE,∴BE是线段AF的垂直平分线,∴AB=BF=BC+CF=BC+AD.
_21?????????è?????(www???21cnjy???com)_
