29.3 课题学习制作立体模型-2020-2021学年九年级数学下册同步课堂帮帮帮(人教版)
文档属性
| 名称 | 29.3 课题学习制作立体模型-2020-2021学年九年级数学下册同步课堂帮帮帮(人教版) |  | |
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-23 11:18:07 | ||
图片预览



文档简介
第29章投影与视图
29.3课题学习制作立体模型
1.乘根据三视图制作立体模型的实践活动,体验平面图形向立体转化的过程
2.感受立体图形与平面图形之间的联系 图形.
1.数学是以数量关系和空间形式为主要研究对象的科学,数量关系和空间形式是从现实世界中抽象出来的.
很明显,关于投影和视图的知识是从实际需要(建筑、制造等)中产生的,它们与实际模型联系得非常紧密.
感性认识需要上升为理性认识,理论指导下的实践会更明确有效.
从技能上说,认识平面图形与立体图形的联系,有助于根据需要实现它们之间的相互转化,即学会画三视图和由三视图得出立体图形.从能力上说,认识平面图形与立体图形的联系,对于培养空间想象能力上非常重要的.
一、单选题
1.用平面去截一个几何体,如果截面的形状是长方形,则原来的几何体不可能是( )
A.正方体 B.棱柱体 C.圆柱 D.圆锥
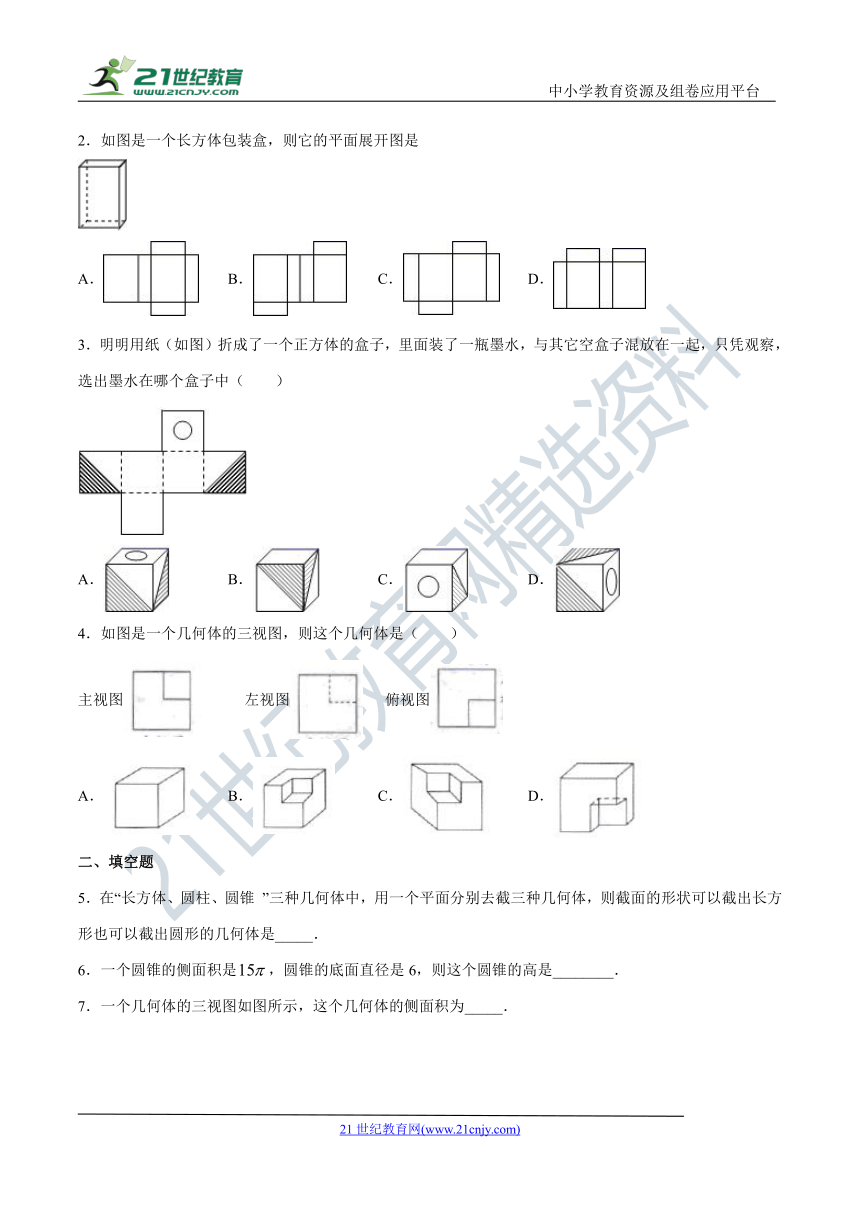
2.如图是一个长方体包装盒,则它的平面展开图是
A. B. C. D.
3.明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )
?
A.? B.? C.? D.?
4.如图是一个几何体的三视图,则这个几何体是( )
主视图 左视图 俯视图
A. B. C. D.
二、填空题
5.在“长方体、圆柱、圆锥 ”三种几何体中,用一个平面分别去截三种几何体,则截面的形状可以截出长方形也可以截出圆形的几何体是_____.
6.一个圆锥的侧面积是,圆锥的底面直径是6,则这个圆锥的高是________.
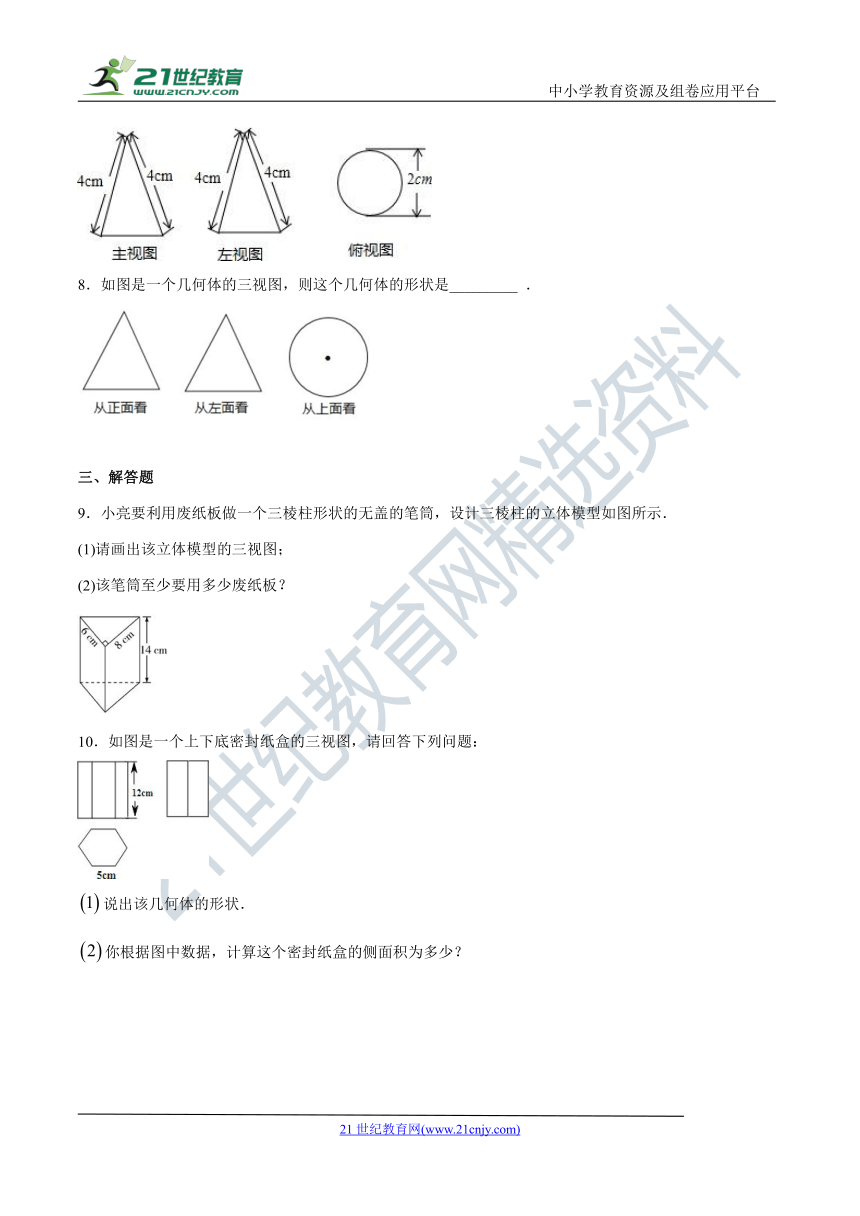
7.一个几何体的三视图如图所示,这个几何体的侧面积为_____.
8.如图是一个几何体的三视图,则这个几何体的形状是_________ .
三、解答题
9.小亮要利用废纸板做一个三棱柱形状的无盖的笔筒,设计三棱柱的立体模型如图所示.
(1)请画出该立体模型的三视图;
(2)该笔筒至少要用多少废纸板?
10.如图是一个上下底密封纸盒的三视图,请回答下列问题:
说出该几何体的形状.
你根据图中数据,计算这个密封纸盒的侧面积为多少?
参考答案
1.D
【解析】
【分析】
根据正方体、棱柱、圆锥、圆柱的特点,以及横截面或纵截面的特点进行判断即可.
【详解】
A、正方体的截面可以是长方形,不符合题意;
B、棱柱的截面可以是长方形,不符合题意;
C、圆柱的横截面或纵截面中有一个为矩形,不符合题意;
D、圆锥有一个平面和一个曲面,截面最多有三条边,截面不可能是长方形,符合题意.
故选:D.
【点睛】
本题主要考查了截一个几何体,明确截面的形状既与被截的几何体有关,还与截面的角度和方向有关是解题的关键.
2.A
【解析】
试题分析:由四棱柱四个侧面和上下两个底面的特征可知,A、可以拼成一个长方体,B、C、D、不符合长方体的展开图的特征,故不是长方体的展开图.故选A.
考点:几何体的展开图.
3.B
【解析】
试题分析:根据展开图中各种符号的特征和位置,可得墨水在B盒子里面.
故选B.
考点:展开图折叠成几何体.
4.B
【解析】
【分析】
结合三视图确定小正方体的位置后即可确定正确的选项.
【详解】
解:结合三个视图发现,应该是由一个正方体在一个角上挖去一个小正方体,且小正方体的位置应该在右上角,
故选B.
【点睛】
本题考查由三视图判断几何体的知识,解题的关键是能够正确的确定小正方体的位置,难度不大.
5.圆柱
【解析】
【分析】
首先当截面的角度和方向不同时,长方体的截面始终不是圆,无论什么方向截取圆锥都不会截得长方形,从而可用排除法可得答案.
【详解】
解:用一个平面截长方体,不管角度与方向,始终截不到圆,所以排除长方体,
用一个平面截圆锥,不管角度与方向,始终截不到长方形,所以排除圆锥,
用一个平面截圆柱,可以截到长方形与圆.
故答案为:圆柱.
【点睛】
本题考查的是对基本的几何立体图形的认识,掌握长方体,圆柱,圆锥的特点是解题的关键.
6.4
【解析】
【分析】
根据圆锥的侧面积=π×底面半径×母线长求得圆锥的母线长,然后利用勾股定理求得圆锥的高即可.
【详解】
解:设圆锥的母线长为x, 由题意得:15π=πx×3, 解得x=5,
所以圆锥的高为,
故答案为:4.
【点睛】
本题考查圆锥的计算,解题的关键熟练掌握是圆锥侧面积的计算公式.
7.4πcm2.
【解析】
【分析】
关键几何体的三视图确定几何体形状,再根据圆锥侧面积的计算方法计算侧面积.
【详解】
解:此几何体为圆锥;
∵直径为,母线长为,
∴侧面积=.
故答案为.
【点睛】
此题重点考查学生对几何体三视图的应用,掌握几何体三视图是解题的关键.
8.圆锥
【解析】
【分析】
根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,再根据几何体的特点即可得出答案.
【详解】
根据俯视图为圆的有球,圆锥,圆柱等几何体,主视图和左视图为三角形的只有圆锥,则这个几何体的形状是圆锥.
故答案为圆锥.
【点睛】
本题考查了由三视图判断几何体,关键是对三视图能熟练掌握和灵活运用,体现了对空间想象能力的考查.
9.(1)见解析;(2) 360 cm2.
【解析】
【分析】
(1)主视图应为一个长方形里有一条竖直的实线;左视图为一个长方形,俯视图为一个三角形.?
(2)由图可知三角形为直角三角形,根据勾股定理得到斜边的长,再根据长方形和三角形的面积公式计算即可求解.
【详解】
解:(1)三视图如图所示.
(2) ∵ 三角形为直角三角形,
∴斜边的长为:,
∴矩形面积和为(6+8+10)×14=24×14=336(cm2),
直角三角形面积为×8×6=24(cm2),
表面积为336+24=360(cm2),
∴该笔筒至少要用废纸板360 cm2.
【点睛】
本题考查了三视图的画法及相关计算,掌握三视图的画法是解题的关键;用到的知识点为:三视图为主视图,左视图,俯视图,分别是从物体的正面,左面,上面看得到的图形.考查了学生的空间想象能力.
10.(1)六棱柱;(2).
【解析】
【分析】
(1)由该几何体的三视图知道其是一个六棱柱;
(2)根据(1)可知其侧面是6个矩形,利用矩形的面积公式求解即可.
【详解】
解:由该几何体的三视图知道其是一个六棱柱;
∵其高为,底面多边形边长为,
∴其侧面积为.
故这个密封纸盒的侧面积为.
【点睛】
本题考查了由三视图判断几何体及求立体图形侧面积的知识,解题的关键是正确的判定几何体.
一、单选题
1.如图是某几何体的俯视阁,那么这个几何体可以是( )
A. B. C. D.
2.如图是由一些棱长为1的小正方体搭成的几何体的三视图.若在所搭几何体的基础上(不改变原几何体中小正方体的位置),继续添加相同的小正方体,以搭成一个长方体,至少还需要小正方体的个数为( )
A.24 B.25 C.26 D.27
3.将下面的纸片沿虚线折叠,不能折成长方体盒子的是( )
A. B. C. D.
4.一个几何体的三视图如图所示,则该几何体的表面积是( )
A.24+2π B.16+4π C.16+8π D.16+12π
二、填空题
5.已知几何体的三视图如图,则该物体的体积为_____.
6.如图,是由一些相同的小正方体搭成的几何体从三个方向看到的图形,搭成这个几何体的小正方体的个数是_______.
7.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有乙滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外币A处到达内壁B处的最短距离为_______.
8.如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为 cm2.(结果可保留根号)
三、解答题
9.(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名是从哪个方向看的;(填正面或上面)
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积和体积.(用含π的式子表示)
10.有一张长 9cm,宽 5cm 的长方形硬纸板,如图在长方形硬纸板的四个角上各截去一个边长为 0.5cm 的正方形,如图①所示,然后把它折叠成一个无盖的长方体小盒,如图②所示.
请问:
(1)折叠成一个无盖的长方体小盒的地面长.宽分别是多少?
(2)这个硬纸板折叠成的小盒容积是多大?
参考答案
1.C
【解析】
【分析】
分别找到图形的三视图进行对比即可解题.
【详解】
解:A的俯视图中间应该是正方形,
B的俯视图应该是不相切的圆,
C的俯视图正确,
D的俯视图中心不是圆,
故选C.
【点睛】
主视图是在物体正面从前向后观察物体得到的图形;俯视图是站在物体的正面从上向下观察物体得到的图形;左视图是在物体正面从左向右观察到的图形,掌握三视图的定义是解题关键.
2.C
【解析】
【分析】
首先根据该几何体的三视图确定需要的小立方块的块数分布情况,然后确定搭成一个大长方体需要的块数.
【详解】
解:由俯视图易得最底层有7个小立方体,第二层有2个小立方体,第三层有1小立方体,其小正方块分布情况如下:
那么共有7+2+1=10个几何体组成.若搭成一个大长方体,共需3×4×3=36个小立方体,所以还需36-10=26个小立方体.
故选:C.
【点睛】
本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
3.D
【解析】
【分析】
直接利用长方体展开图的特点进而得出答案.
【详解】
解:选项A,B,C都能折叠成长方体盒子,选项D上面部分重叠无法折叠成长方体盒子.
故选D.
【点睛】
本题考查展开图折叠成几何体,正确掌握基本图形的展开图的形状是解题关键.
4.D
【解析】
【分析】
根据三视图知该几何体是一个半径为2、高为4的圆柱体的纵向一半,据此求解可得.
【详解】
该几何体的表面积为2×?π?22+4×4+×2π?2×4=12π+16,
故选D.
【点睛】
本题主要考查由三视图判断几何体,解题的关键是根据三视图得出几何体的形状及圆柱体的有关计算.
5.
【解析】
【分析】
由三视图知几何体是一个三棱柱,三棱柱底是边长为3cm的正三角形,高为5cm,体积由底面三角形的面积乘高即可得到结果.
【详解】
由三视图知几何体是一个三棱柱,三棱柱底是边长为3cm的正三角形,高为5cm,
∴三棱柱的体积是×3××3×5=,
故答案为:.
【点睛】
本题考查由三视图还原几何体并且求几何体的体积,本题解题的关键是看出几何体各个部分的长度,本题是一个基础题.
6.4
【解析】
【分析】
根据“从正面看”可得该几何体有2层,再分别根据“从左面看”、“从上面看”,判断该几何体有几行、几列以及正方体的具体摆放,即可解答.
【详解】
观察三视图,可得这个几何体有两层,底下一层是一行三列有3个正方体,上面一层最右边有一个正方体,
故搭成这个几何体的小正方体的个数为3+1=4个.
故答案为4.
【点睛】
本题考查对三视图的理解应用以及空间想象能力,可从主视图分清物体的上下和左右的层数,从俯视图上分清物体的左右和前后的位置,综合上述分析出小立方体的个数.
7.20 cm.
【解析】
【分析】
将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
【详解】
解:如答图,将杯子侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离.
根据勾股定理,得(cm).
故答案为:20cm.
【点睛】
本题考查了平面展开---最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
8.(75+360).
【解析】
【分析】
【详解】
根据该几何体的三视图知道其是一个六棱柱,
∵其高为12cm,底面半径为5,
∴其侧面积为6×5×12=360cm2
密封纸盒的侧面积为:×5×6×5=75cm2
∴其全面积为:(75+360)cm2.
9.(1)正面、 上面;(2)表面积:132+24π;体积:80+24π
【解析】
【分析】
(1)找到从正面和上面看所得到的图形即可,注意所有的看到的棱都应表现在视图中.
(2)根据题目所给尺寸,计算出下面长方体表面积+上面圆柱的侧面积.
【详解】
解:(1)正面、 上面
(2)表面积: 2(8×5+8×2+5×2)+4×π×6
=2(8×5+8×2+5×2)+4×π×6
=132+24π(cm2).
体积: 8×5×2+4×π×6
=2(8×5+8×2+5×2)+4×π×6
=80+24π(cm3)
【点睛】
此题主要考查了简单几何体的三视图,求几何体的表面积和几何体的体积,解题关键是数形结合.
10.(1)8,4;(2)16
【解析】
【分析】
(1)首先根据题意,用长方形硬纸板的长减去小正方形的边长的2倍,求出长方体纸盒的长是多少;然后用长方形硬纸板的宽减去小正方形的边长的2倍,求出长方体纸盒的宽是多少;(2)根据长方体的容积=长×宽×高,求出这个纸盒的容积是多少立方厘米即可.
【详解】
解:由题意得(1)无盖的长方体小盒的长=9-2×0.5=8
无盖的长方体小盒的宽=5-2×0.5=4;
(2)小盒的容积=8×4×0.5=16(立方厘米)
故答案为(1)8,4;(2)16.
【点睛】
本题主要考查长方体的体积(容积)计算的实际应用,关键是求得盒子的长、宽、高各是多少.
一、单选题
1.(2018·山东威海·中考真题)如图是某圆锥的主视图和左视图,该圆锥的侧面积是( )
A.25π B.24π C.20π D.15π
2.(2014·内蒙古呼和浩特·中考真题)如图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A.60π B.70π C.90π D.160π
3.(2015·四川达州·中考真题)一个几何体由大小相同的小方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状图是( )
A. B. C. D.
4.(2015·山东日照·中考真题)小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )
A.3个 B.4个 C.5个 D.6个
5.(2015·黑龙江绥化·中考真题)左下图是一些完全相同的小正方体搭成的几何体的三视图 .这个几何体只能是( )
A. B. C. D.
6.(2013·浙江温州·中考真题)下列各图中,经过折叠能围成一个正方体的是( )
A. B. C. D.
二、填空题
7.(2017·宁夏中考真题)如图是由若干个棱长为2的小正方体组合而成的一个几何体的三视图,则这个几何体的体积是________.
8.(2012·湖北荆门·中考真题)如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为 cm2.(结果可保留根号)
参考答案
1.C
【解析】
分析:求得圆锥的底面周长以及母线长,即可得到圆锥的侧面积.
详解:由题可得,圆锥的底面直径为8,高为3,
∴圆锥的底面周长为8π,
圆锥的母线长为=5,
∴圆锥的侧面积=×8π×5=20π,
故选C.
点睛:本题主要考查了由三视图判断几何体以及圆锥的计算,圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
2.B
【解析】
试题分析:由几何体的三视图得,几何体是高为10,外径为8.内径为6的圆筒,
∴该几何体的体积为.
故选B.
考点:由三视图求体积.
3.D
【解析】
试题分析:根据所给出的图形和数字可得:主视图有3列,每列小正方形数目分别为3,2,3,
则符合题意的是D;
故选D.
考点:1.由三视图判断几何体;2.作图-三视图.
4.B
【解析】
试题分析:从俯视图发现有3个立方体,从左视图发现第二层最多有1个立方块,
则构成该几何体的小立方块的个数有4个;
故选B.
考点: 由三视图判断几何体.
5.A
【解析】
试题分析:根据几何体的主视图可判断C不合题意;根据左视图可得B、D不合题意,因此选项A正确,故选A.
考点:几何体的三视图
6.A
【解析】
由平面图形的折叠及正方体的展开图解题,注意只要有“田”、“凹”字格的展开图都不是正方体的表面展开图.
A、可以折叠成一个正方体;
B、是“凹”字格,故不能折叠成一个正方体;
C、折叠后有两个面重合,缺少一个底面,所以也不能折叠成一个正方体;
D、是“田”字格,故不能折叠成一个正方体.
故选A.
7.40
【解析】
试题分析:利用主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,进而判断图形形状,即可得出小正方体的个数.
综合三视图,我们可以得出,这个几何模型的底层有3+1=4个小正方体,第二有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是4+1=5个.
∴这个几何体的表面积是5×6﹣8=22,
故答案为22.
考点:三视图.
8.(75+360).
【解析】
【分析】
【详解】
根据该几何体的三视图知道其是一个六棱柱,
∵其高为12cm,底面半径为5,
∴其侧面积为6×5×12=360cm2
密封纸盒的侧面积为:×5×6×5=75cm2
∴其全面积为:(75+360)cm2.
29.3课题学习制作立体模型
1.乘根据三视图制作立体模型的实践活动,体验平面图形向立体转化的过程
2.感受立体图形与平面图形之间的联系 图形.
1.数学是以数量关系和空间形式为主要研究对象的科学,数量关系和空间形式是从现实世界中抽象出来的.
很明显,关于投影和视图的知识是从实际需要(建筑、制造等)中产生的,它们与实际模型联系得非常紧密.
感性认识需要上升为理性认识,理论指导下的实践会更明确有效.
从技能上说,认识平面图形与立体图形的联系,有助于根据需要实现它们之间的相互转化,即学会画三视图和由三视图得出立体图形.从能力上说,认识平面图形与立体图形的联系,对于培养空间想象能力上非常重要的.
一、单选题
1.用平面去截一个几何体,如果截面的形状是长方形,则原来的几何体不可能是( )
A.正方体 B.棱柱体 C.圆柱 D.圆锥
2.如图是一个长方体包装盒,则它的平面展开图是
A. B. C. D.
3.明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )
?
A.? B.? C.? D.?
4.如图是一个几何体的三视图,则这个几何体是( )
主视图 左视图 俯视图
A. B. C. D.
二、填空题
5.在“长方体、圆柱、圆锥 ”三种几何体中,用一个平面分别去截三种几何体,则截面的形状可以截出长方形也可以截出圆形的几何体是_____.
6.一个圆锥的侧面积是,圆锥的底面直径是6,则这个圆锥的高是________.
7.一个几何体的三视图如图所示,这个几何体的侧面积为_____.
8.如图是一个几何体的三视图,则这个几何体的形状是_________ .
三、解答题
9.小亮要利用废纸板做一个三棱柱形状的无盖的笔筒,设计三棱柱的立体模型如图所示.
(1)请画出该立体模型的三视图;
(2)该笔筒至少要用多少废纸板?
10.如图是一个上下底密封纸盒的三视图,请回答下列问题:
说出该几何体的形状.
你根据图中数据,计算这个密封纸盒的侧面积为多少?
参考答案
1.D
【解析】
【分析】
根据正方体、棱柱、圆锥、圆柱的特点,以及横截面或纵截面的特点进行判断即可.
【详解】
A、正方体的截面可以是长方形,不符合题意;
B、棱柱的截面可以是长方形,不符合题意;
C、圆柱的横截面或纵截面中有一个为矩形,不符合题意;
D、圆锥有一个平面和一个曲面,截面最多有三条边,截面不可能是长方形,符合题意.
故选:D.
【点睛】
本题主要考查了截一个几何体,明确截面的形状既与被截的几何体有关,还与截面的角度和方向有关是解题的关键.
2.A
【解析】
试题分析:由四棱柱四个侧面和上下两个底面的特征可知,A、可以拼成一个长方体,B、C、D、不符合长方体的展开图的特征,故不是长方体的展开图.故选A.
考点:几何体的展开图.
3.B
【解析】
试题分析:根据展开图中各种符号的特征和位置,可得墨水在B盒子里面.
故选B.
考点:展开图折叠成几何体.
4.B
【解析】
【分析】
结合三视图确定小正方体的位置后即可确定正确的选项.
【详解】
解:结合三个视图发现,应该是由一个正方体在一个角上挖去一个小正方体,且小正方体的位置应该在右上角,
故选B.
【点睛】
本题考查由三视图判断几何体的知识,解题的关键是能够正确的确定小正方体的位置,难度不大.
5.圆柱
【解析】
【分析】
首先当截面的角度和方向不同时,长方体的截面始终不是圆,无论什么方向截取圆锥都不会截得长方形,从而可用排除法可得答案.
【详解】
解:用一个平面截长方体,不管角度与方向,始终截不到圆,所以排除长方体,
用一个平面截圆锥,不管角度与方向,始终截不到长方形,所以排除圆锥,
用一个平面截圆柱,可以截到长方形与圆.
故答案为:圆柱.
【点睛】
本题考查的是对基本的几何立体图形的认识,掌握长方体,圆柱,圆锥的特点是解题的关键.
6.4
【解析】
【分析】
根据圆锥的侧面积=π×底面半径×母线长求得圆锥的母线长,然后利用勾股定理求得圆锥的高即可.
【详解】
解:设圆锥的母线长为x, 由题意得:15π=πx×3, 解得x=5,
所以圆锥的高为,
故答案为:4.
【点睛】
本题考查圆锥的计算,解题的关键熟练掌握是圆锥侧面积的计算公式.
7.4πcm2.
【解析】
【分析】
关键几何体的三视图确定几何体形状,再根据圆锥侧面积的计算方法计算侧面积.
【详解】
解:此几何体为圆锥;
∵直径为,母线长为,
∴侧面积=.
故答案为.
【点睛】
此题重点考查学生对几何体三视图的应用,掌握几何体三视图是解题的关键.
8.圆锥
【解析】
【分析】
根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,再根据几何体的特点即可得出答案.
【详解】
根据俯视图为圆的有球,圆锥,圆柱等几何体,主视图和左视图为三角形的只有圆锥,则这个几何体的形状是圆锥.
故答案为圆锥.
【点睛】
本题考查了由三视图判断几何体,关键是对三视图能熟练掌握和灵活运用,体现了对空间想象能力的考查.
9.(1)见解析;(2) 360 cm2.
【解析】
【分析】
(1)主视图应为一个长方形里有一条竖直的实线;左视图为一个长方形,俯视图为一个三角形.?
(2)由图可知三角形为直角三角形,根据勾股定理得到斜边的长,再根据长方形和三角形的面积公式计算即可求解.
【详解】
解:(1)三视图如图所示.
(2) ∵ 三角形为直角三角形,
∴斜边的长为:,
∴矩形面积和为(6+8+10)×14=24×14=336(cm2),
直角三角形面积为×8×6=24(cm2),
表面积为336+24=360(cm2),
∴该笔筒至少要用废纸板360 cm2.
【点睛】
本题考查了三视图的画法及相关计算,掌握三视图的画法是解题的关键;用到的知识点为:三视图为主视图,左视图,俯视图,分别是从物体的正面,左面,上面看得到的图形.考查了学生的空间想象能力.
10.(1)六棱柱;(2).
【解析】
【分析】
(1)由该几何体的三视图知道其是一个六棱柱;
(2)根据(1)可知其侧面是6个矩形,利用矩形的面积公式求解即可.
【详解】
解:由该几何体的三视图知道其是一个六棱柱;
∵其高为,底面多边形边长为,
∴其侧面积为.
故这个密封纸盒的侧面积为.
【点睛】
本题考查了由三视图判断几何体及求立体图形侧面积的知识,解题的关键是正确的判定几何体.
一、单选题
1.如图是某几何体的俯视阁,那么这个几何体可以是( )
A. B. C. D.
2.如图是由一些棱长为1的小正方体搭成的几何体的三视图.若在所搭几何体的基础上(不改变原几何体中小正方体的位置),继续添加相同的小正方体,以搭成一个长方体,至少还需要小正方体的个数为( )
A.24 B.25 C.26 D.27
3.将下面的纸片沿虚线折叠,不能折成长方体盒子的是( )
A. B. C. D.
4.一个几何体的三视图如图所示,则该几何体的表面积是( )
A.24+2π B.16+4π C.16+8π D.16+12π
二、填空题
5.已知几何体的三视图如图,则该物体的体积为_____.
6.如图,是由一些相同的小正方体搭成的几何体从三个方向看到的图形,搭成这个几何体的小正方体的个数是_______.
7.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有乙滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外币A处到达内壁B处的最短距离为_______.
8.如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为 cm2.(结果可保留根号)
三、解答题
9.(1)如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名是从哪个方向看的;(填正面或上面)
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积和体积.(用含π的式子表示)
10.有一张长 9cm,宽 5cm 的长方形硬纸板,如图在长方形硬纸板的四个角上各截去一个边长为 0.5cm 的正方形,如图①所示,然后把它折叠成一个无盖的长方体小盒,如图②所示.
请问:
(1)折叠成一个无盖的长方体小盒的地面长.宽分别是多少?
(2)这个硬纸板折叠成的小盒容积是多大?
参考答案
1.C
【解析】
【分析】
分别找到图形的三视图进行对比即可解题.
【详解】
解:A的俯视图中间应该是正方形,
B的俯视图应该是不相切的圆,
C的俯视图正确,
D的俯视图中心不是圆,
故选C.
【点睛】
主视图是在物体正面从前向后观察物体得到的图形;俯视图是站在物体的正面从上向下观察物体得到的图形;左视图是在物体正面从左向右观察到的图形,掌握三视图的定义是解题关键.
2.C
【解析】
【分析】
首先根据该几何体的三视图确定需要的小立方块的块数分布情况,然后确定搭成一个大长方体需要的块数.
【详解】
解:由俯视图易得最底层有7个小立方体,第二层有2个小立方体,第三层有1小立方体,其小正方块分布情况如下:
那么共有7+2+1=10个几何体组成.若搭成一个大长方体,共需3×4×3=36个小立方体,所以还需36-10=26个小立方体.
故选:C.
【点睛】
本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
3.D
【解析】
【分析】
直接利用长方体展开图的特点进而得出答案.
【详解】
解:选项A,B,C都能折叠成长方体盒子,选项D上面部分重叠无法折叠成长方体盒子.
故选D.
【点睛】
本题考查展开图折叠成几何体,正确掌握基本图形的展开图的形状是解题关键.
4.D
【解析】
【分析】
根据三视图知该几何体是一个半径为2、高为4的圆柱体的纵向一半,据此求解可得.
【详解】
该几何体的表面积为2×?π?22+4×4+×2π?2×4=12π+16,
故选D.
【点睛】
本题主要考查由三视图判断几何体,解题的关键是根据三视图得出几何体的形状及圆柱体的有关计算.
5.
【解析】
【分析】
由三视图知几何体是一个三棱柱,三棱柱底是边长为3cm的正三角形,高为5cm,体积由底面三角形的面积乘高即可得到结果.
【详解】
由三视图知几何体是一个三棱柱,三棱柱底是边长为3cm的正三角形,高为5cm,
∴三棱柱的体积是×3××3×5=,
故答案为:.
【点睛】
本题考查由三视图还原几何体并且求几何体的体积,本题解题的关键是看出几何体各个部分的长度,本题是一个基础题.
6.4
【解析】
【分析】
根据“从正面看”可得该几何体有2层,再分别根据“从左面看”、“从上面看”,判断该几何体有几行、几列以及正方体的具体摆放,即可解答.
【详解】
观察三视图,可得这个几何体有两层,底下一层是一行三列有3个正方体,上面一层最右边有一个正方体,
故搭成这个几何体的小正方体的个数为3+1=4个.
故答案为4.
【点睛】
本题考查对三视图的理解应用以及空间想象能力,可从主视图分清物体的上下和左右的层数,从俯视图上分清物体的左右和前后的位置,综合上述分析出小立方体的个数.
7.20 cm.
【解析】
【分析】
将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
【详解】
解:如答图,将杯子侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离.
根据勾股定理,得(cm).
故答案为:20cm.
【点睛】
本题考查了平面展开---最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.
8.(75+360).
【解析】
【分析】
【详解】
根据该几何体的三视图知道其是一个六棱柱,
∵其高为12cm,底面半径为5,
∴其侧面积为6×5×12=360cm2
密封纸盒的侧面积为:×5×6×5=75cm2
∴其全面积为:(75+360)cm2.
9.(1)正面、 上面;(2)表面积:132+24π;体积:80+24π
【解析】
【分析】
(1)找到从正面和上面看所得到的图形即可,注意所有的看到的棱都应表现在视图中.
(2)根据题目所给尺寸,计算出下面长方体表面积+上面圆柱的侧面积.
【详解】
解:(1)正面、 上面
(2)表面积: 2(8×5+8×2+5×2)+4×π×6
=2(8×5+8×2+5×2)+4×π×6
=132+24π(cm2).
体积: 8×5×2+4×π×6
=2(8×5+8×2+5×2)+4×π×6
=80+24π(cm3)
【点睛】
此题主要考查了简单几何体的三视图,求几何体的表面积和几何体的体积,解题关键是数形结合.
10.(1)8,4;(2)16
【解析】
【分析】
(1)首先根据题意,用长方形硬纸板的长减去小正方形的边长的2倍,求出长方体纸盒的长是多少;然后用长方形硬纸板的宽减去小正方形的边长的2倍,求出长方体纸盒的宽是多少;(2)根据长方体的容积=长×宽×高,求出这个纸盒的容积是多少立方厘米即可.
【详解】
解:由题意得(1)无盖的长方体小盒的长=9-2×0.5=8
无盖的长方体小盒的宽=5-2×0.5=4;
(2)小盒的容积=8×4×0.5=16(立方厘米)
故答案为(1)8,4;(2)16.
【点睛】
本题主要考查长方体的体积(容积)计算的实际应用,关键是求得盒子的长、宽、高各是多少.
一、单选题
1.(2018·山东威海·中考真题)如图是某圆锥的主视图和左视图,该圆锥的侧面积是( )
A.25π B.24π C.20π D.15π
2.(2014·内蒙古呼和浩特·中考真题)如图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A.60π B.70π C.90π D.160π
3.(2015·四川达州·中考真题)一个几何体由大小相同的小方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状图是( )
A. B. C. D.
4.(2015·山东日照·中考真题)小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )
A.3个 B.4个 C.5个 D.6个
5.(2015·黑龙江绥化·中考真题)左下图是一些完全相同的小正方体搭成的几何体的三视图 .这个几何体只能是( )
A. B. C. D.
6.(2013·浙江温州·中考真题)下列各图中,经过折叠能围成一个正方体的是( )
A. B. C. D.
二、填空题
7.(2017·宁夏中考真题)如图是由若干个棱长为2的小正方体组合而成的一个几何体的三视图,则这个几何体的体积是________.
8.(2012·湖北荆门·中考真题)如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为 cm2.(结果可保留根号)
参考答案
1.C
【解析】
分析:求得圆锥的底面周长以及母线长,即可得到圆锥的侧面积.
详解:由题可得,圆锥的底面直径为8,高为3,
∴圆锥的底面周长为8π,
圆锥的母线长为=5,
∴圆锥的侧面积=×8π×5=20π,
故选C.
点睛:本题主要考查了由三视图判断几何体以及圆锥的计算,圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
2.B
【解析】
试题分析:由几何体的三视图得,几何体是高为10,外径为8.内径为6的圆筒,
∴该几何体的体积为.
故选B.
考点:由三视图求体积.
3.D
【解析】
试题分析:根据所给出的图形和数字可得:主视图有3列,每列小正方形数目分别为3,2,3,
则符合题意的是D;
故选D.
考点:1.由三视图判断几何体;2.作图-三视图.
4.B
【解析】
试题分析:从俯视图发现有3个立方体,从左视图发现第二层最多有1个立方块,
则构成该几何体的小立方块的个数有4个;
故选B.
考点: 由三视图判断几何体.
5.A
【解析】
试题分析:根据几何体的主视图可判断C不合题意;根据左视图可得B、D不合题意,因此选项A正确,故选A.
考点:几何体的三视图
6.A
【解析】
由平面图形的折叠及正方体的展开图解题,注意只要有“田”、“凹”字格的展开图都不是正方体的表面展开图.
A、可以折叠成一个正方体;
B、是“凹”字格,故不能折叠成一个正方体;
C、折叠后有两个面重合,缺少一个底面,所以也不能折叠成一个正方体;
D、是“田”字格,故不能折叠成一个正方体.
故选A.
7.40
【解析】
试题分析:利用主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,进而判断图形形状,即可得出小正方体的个数.
综合三视图,我们可以得出,这个几何模型的底层有3+1=4个小正方体,第二有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是4+1=5个.
∴这个几何体的表面积是5×6﹣8=22,
故答案为22.
考点:三视图.
8.(75+360).
【解析】
【分析】
【详解】
根据该几何体的三视图知道其是一个六棱柱,
∵其高为12cm,底面半径为5,
∴其侧面积为6×5×12=360cm2
密封纸盒的侧面积为:×5×6×5=75cm2
∴其全面积为:(75+360)cm2.
