高中物理人教版必修2 课后练习题 5-6 向心力 Word版含解析
文档属性
| 名称 | 高中物理人教版必修2 课后练习题 5-6 向心力 Word版含解析 |  | |
| 格式 | DOC | ||
| 文件大小 | 678.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-19 12:04:46 | ||
图片预览


文档简介
向心力
一、单项选择题
1.如图所示,一圆盘可绕一通过圆心且垂直于盘面的竖直轴转动,在圆盘上放一块橡皮,橡皮块随圆盘一起转动(俯视为逆时针).某段时间圆盘转速不断增大,但橡皮块仍相对圆盘静止,在这段时间内,关于橡皮块所受合力F的方向的四种表示(俯视图)中,正确的是( C )
解析:橡皮块做加速圆周运动,合力不指向圆心,但一定指向圆周的内侧;合力的径向分力提供向心力,切线分力产生切向加速度.由于做加速圆周运动,转速不断增加,故合力与速度的夹角小于90°;故选C.
2.如图所示,某电视台推出了一款娱乐闯关节目,选手最容易失败落水的地方是“疯狂转盘”和“高空滑索”.根据所学物理知识,选出选项中表述正确的选项( A )
A.选手进入转盘后,在转盘中间比较安全
B.选手进入转盘后,在转盘边缘比较安全
C.质量越大的选手,在转盘上越不容易落水
D.选手从最后一个转盘的边缘起跳去抓滑索时,起跳方向应正对悬索
解析:根据向心力Fn=4π2mn2r,在转盘转速不变的情况下,半径越大,需要的向心力越大,而质量一定的选手最大静摩擦力是确定的,所以在转盘中间比较安全,A对、B错.向心力由摩擦力提供,μmg=,可见是否容易落水和选手质量无关,C错.选手从转盘的边缘起跳时,有一个与转盘边缘线速度一样的分速度,所以选手起跳方向不应正对悬索,D错.
3.如图所示,一个匀速转动的半径为r的水平圆盘上放着两个小木块M和N,木块M放在圆盘的边缘处,木块N放在离圆心r处,它们都随圆盘一起运动.下列说法中正确的是( D )
A.M受到重力、支持力、向心力
B.M、N两木块的线速度相等
C.M的角速度是N的3倍
D.M的向心加速度是N的3倍
解析:小木块做匀速圆周运动,合力指向圆心,对木块受力分析,受重力、支持力和静摩擦力,合力提供向心力,故A错误;物块与圆盘一起运动,角速度相等,而半径不等,根据v=rω可知,线速度不等,故B、C错误;M的半径是N的3倍,根据a=ω2r可知,M的向心加速度是N的3倍,故D正确.
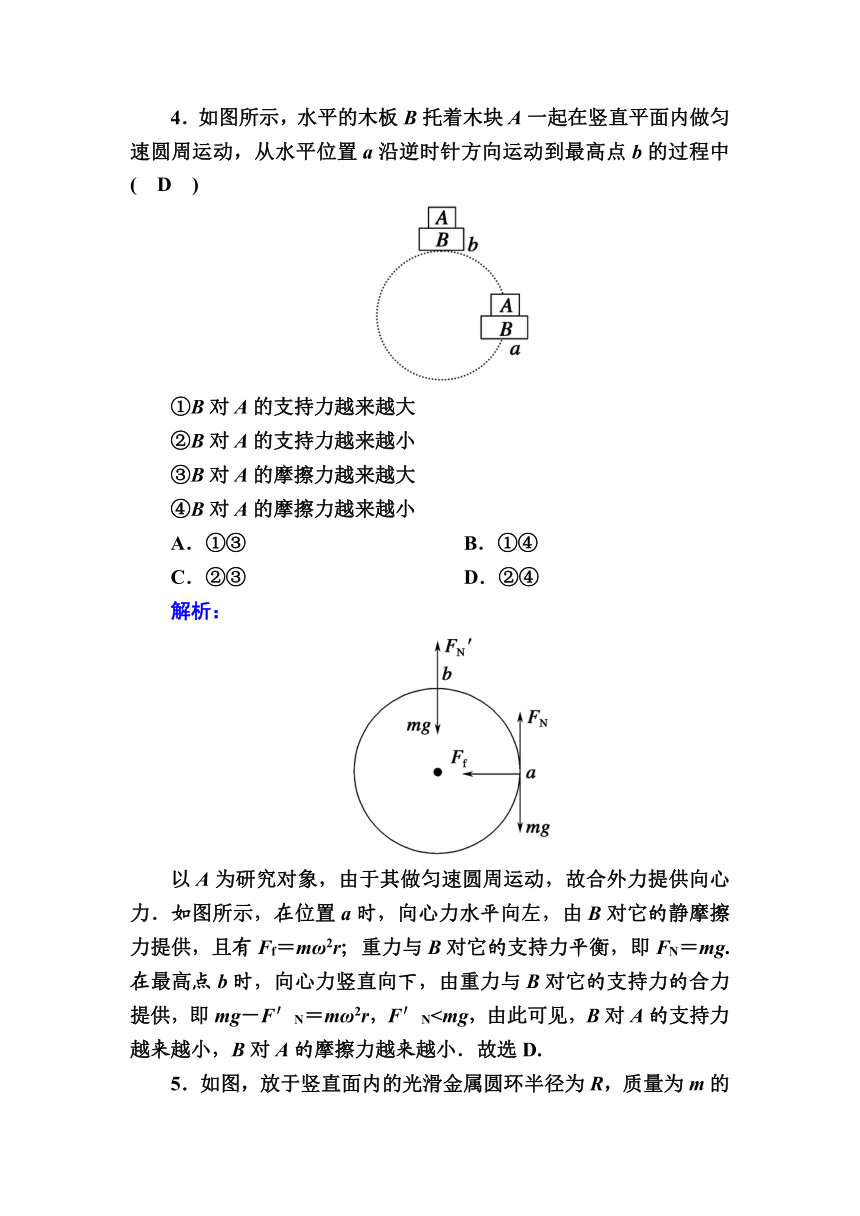
4.如图所示,水平的木板B托着木块A一起在竖直平面内做匀速圆周运动,从水平位置a沿逆时针方向运动到最高点b的过程中( D )
①B对A的支持力越来越大
②B对A的支持力越来越小
③B对A的摩擦力越来越大
④B对A的摩擦力越来越小
A.①③ B.①④
C.②③ D.②④
解析:
以A为研究对象,由于其做匀速圆周运动,故合外力提供向心力.如图所示,在位置a时,向心力水平向左,由B对它的静摩擦力提供,且有Ff=mω2r;重力与B对它的支持力平衡,即FN=mg.在最高点b时,向心力竖直向下,由重力与B对它的支持力的合力提供,即mg-F′N=mω2r,F′N5.如图,放于竖直面内的光滑金属圆环半径为R,质量为m的带孔小球穿于环上,同时有一长也为R的细绳一端系于球上,另一端系于圆环最低点.当圆环以角速度ω绕竖直直径转动时,绳被拉直且小球受两个力作用.则ω为( D )
A. B.
C. D.
解析:小球受重力和圆环的弹力,两个力的合力垂直于转轴,提供向心力,根据牛顿第二定律有:F合=mgcot30°=mRcos30°ω2,解得ω=.故D正确,A、B、C错误.
二、多项选择题
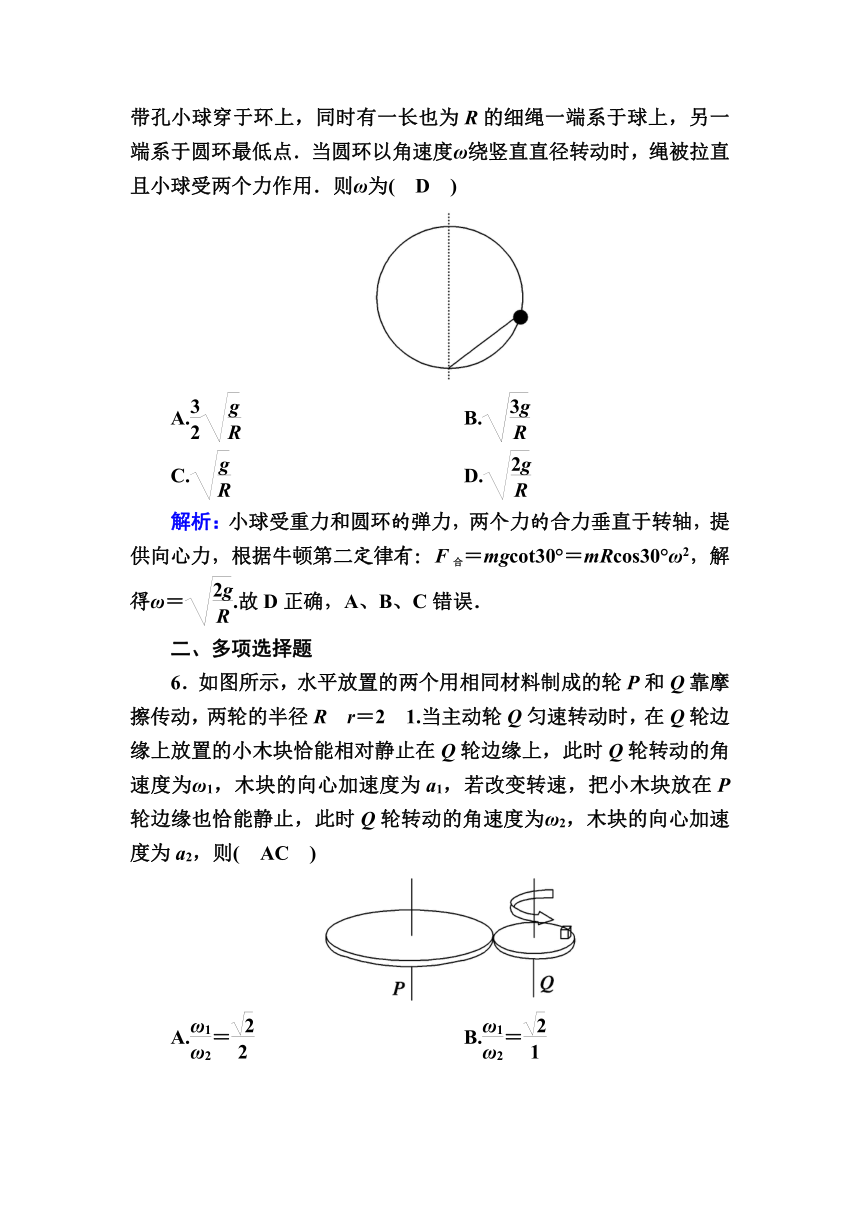
6.如图所示,水平放置的两个用相同材料制成的轮P和Q靠摩擦传动,两轮的半径R?r=2?1.当主动轮Q匀速转动时,在Q轮边缘上放置的小木块恰能相对静止在Q轮边缘上,此时Q轮转动的角速度为ω1,木块的向心加速度为a1,若改变转速,把小木块放在P轮边缘也恰能静止,此时Q轮转动的角速度为ω2,木块的向心加速度为a2,则( AC )
A.= B.=
C.= D.=
解析:根据题述,a1=ωr,ma1=μmg;联立解得μg=ωr.小木块放在P轮边缘也恰能静止,μg=ω2R=2ω2r.由ωR=ω2r联立解得=,选项A正确,B错误;ma=μmg,所以=,选项C正确,D错误.
7.一杂技演员在圆筒状建筑物内表演飞车走壁,最后在直壁上沿水平方向做匀速圆周运动,下列说法中正确的是( AC )
A.车和演员作为一个整体受有重力、竖直壁对车的弹力和摩擦力的作用
B.车和演员做圆周运动所需要的向心力是静摩擦力
C.竖直壁对车的弹力提供向心力,且弹力随车速度的增大而增大
D.竖直壁对车的摩擦力将随车速增加而增加
8.如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动.则下列说法中正确的是( AB )
A.球A的线速度必定大于球B的线速度
B.球A的角速度必定小于球B的角速度
C.球A的运动周期必定小于球B的运动周期
D.球A对筒壁的压力必定大于球B对筒壁的压力
解析:
两球均贴着圆锥筒的内壁,在水平面内做匀速圆周运动,它们均受到重力和筒壁对它们的弹力作用,其合力必定在水平面内时刻指向圆心,如图所示.由图可知,筒壁对球的弹力为,对于A、B两球,因质量相等,θ角也相等,所以A、B两球受到筒壁的弹力大小也相等,由牛顿第三定律知,A、B两球对筒壁的压力大小也相等,D选项不正确.对球运用牛顿第二定律得mgcotθ=m=mω2r=m,球的线速度v=,角速度ω=,周期T=2π.由此可见,球的线速度随轨道半径的增大而增大,所以A球的线速度必定大于B球的线速度,A选项正确.球的角速度随半径的增大而减小,周期随半径的增大而增大,所以A球的角速度小于B球的角速度,A球的周期大于B球的周期,B选项正确,C选项不正确.
三、非选择题
9.如图所示,旋转木马被水平钢杆拴住绕转台的中心轴做匀速圆周运动.若相对两个木马间的杆长为6 m,木马质量为30 kg,骑木马的儿童质量为40 kg,当木马旋转的速度为6 m/s时,试问:
(1)此时木马和儿童的向心力分别是由哪个物体提供的?
(2)此时儿童受到的向心力是多大?
解析:(1)木马受骑在木马上的儿童对它的压力、重力和钢杆对它的作用力做匀速圆周运动.木马受到的向心力由水平钢杆提供;同理可得出儿童受到的向心力由木马提供.
(2)儿童所受向心力由木马提供且指向圆心,则
F向=m=40× N=480 N.
答案:(1)水平钢杆 木马 (2)480 N
10.有一种叫“飞椅”的游乐项目,示意图如图所示,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ.不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.
解析:设转盘转动的角速度为ω时,钢绳与竖直方向的夹角为θ,座椅到中心轴的距离即座椅转动半径为
R=r+Lsinθ.
设钢绳的拉力为FT,对座椅进行受力分析有
竖直方向FTcosθ=mg,水平方向F向=FTsinθ=mRω2,
联立以上各式得ω= .
答案:ω=
11.如图,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径R=0.5 m,离水平地面的高度H=0.8 m,物块平抛落地过程水平位移的大小s=0.4 m.设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2.求:
(1)物块做平抛运动的初速度大小v0;
(2)物块与转台间的动摩擦因数μ.
解析:(1)物块做平抛运动,在竖直方向上有
H=gt2,①
在水平方向上有s=v0t,②
由①②式解得
v0=s,v0=1 m/s.③
(2)物块离开转台时,最大静摩擦力提供向心力,有
F′fm=m,④
Ffm=F′fm=μN=μmg,⑤
由③④⑤式解得μ=,μ=0.2.
答案:(1)1 m/s (2)0.2
一、单项选择题
1.如图所示,一圆盘可绕一通过圆心且垂直于盘面的竖直轴转动,在圆盘上放一块橡皮,橡皮块随圆盘一起转动(俯视为逆时针).某段时间圆盘转速不断增大,但橡皮块仍相对圆盘静止,在这段时间内,关于橡皮块所受合力F的方向的四种表示(俯视图)中,正确的是( C )
解析:橡皮块做加速圆周运动,合力不指向圆心,但一定指向圆周的内侧;合力的径向分力提供向心力,切线分力产生切向加速度.由于做加速圆周运动,转速不断增加,故合力与速度的夹角小于90°;故选C.
2.如图所示,某电视台推出了一款娱乐闯关节目,选手最容易失败落水的地方是“疯狂转盘”和“高空滑索”.根据所学物理知识,选出选项中表述正确的选项( A )
A.选手进入转盘后,在转盘中间比较安全
B.选手进入转盘后,在转盘边缘比较安全
C.质量越大的选手,在转盘上越不容易落水
D.选手从最后一个转盘的边缘起跳去抓滑索时,起跳方向应正对悬索
解析:根据向心力Fn=4π2mn2r,在转盘转速不变的情况下,半径越大,需要的向心力越大,而质量一定的选手最大静摩擦力是确定的,所以在转盘中间比较安全,A对、B错.向心力由摩擦力提供,μmg=,可见是否容易落水和选手质量无关,C错.选手从转盘的边缘起跳时,有一个与转盘边缘线速度一样的分速度,所以选手起跳方向不应正对悬索,D错.
3.如图所示,一个匀速转动的半径为r的水平圆盘上放着两个小木块M和N,木块M放在圆盘的边缘处,木块N放在离圆心r处,它们都随圆盘一起运动.下列说法中正确的是( D )
A.M受到重力、支持力、向心力
B.M、N两木块的线速度相等
C.M的角速度是N的3倍
D.M的向心加速度是N的3倍
解析:小木块做匀速圆周运动,合力指向圆心,对木块受力分析,受重力、支持力和静摩擦力,合力提供向心力,故A错误;物块与圆盘一起运动,角速度相等,而半径不等,根据v=rω可知,线速度不等,故B、C错误;M的半径是N的3倍,根据a=ω2r可知,M的向心加速度是N的3倍,故D正确.
4.如图所示,水平的木板B托着木块A一起在竖直平面内做匀速圆周运动,从水平位置a沿逆时针方向运动到最高点b的过程中( D )
①B对A的支持力越来越大
②B对A的支持力越来越小
③B对A的摩擦力越来越大
④B对A的摩擦力越来越小
A.①③ B.①④
C.②③ D.②④
解析:
以A为研究对象,由于其做匀速圆周运动,故合外力提供向心力.如图所示,在位置a时,向心力水平向左,由B对它的静摩擦力提供,且有Ff=mω2r;重力与B对它的支持力平衡,即FN=mg.在最高点b时,向心力竖直向下,由重力与B对它的支持力的合力提供,即mg-F′N=mω2r,F′N
A. B.
C. D.
解析:小球受重力和圆环的弹力,两个力的合力垂直于转轴,提供向心力,根据牛顿第二定律有:F合=mgcot30°=mRcos30°ω2,解得ω=.故D正确,A、B、C错误.
二、多项选择题
6.如图所示,水平放置的两个用相同材料制成的轮P和Q靠摩擦传动,两轮的半径R?r=2?1.当主动轮Q匀速转动时,在Q轮边缘上放置的小木块恰能相对静止在Q轮边缘上,此时Q轮转动的角速度为ω1,木块的向心加速度为a1,若改变转速,把小木块放在P轮边缘也恰能静止,此时Q轮转动的角速度为ω2,木块的向心加速度为a2,则( AC )
A.= B.=
C.= D.=
解析:根据题述,a1=ωr,ma1=μmg;联立解得μg=ωr.小木块放在P轮边缘也恰能静止,μg=ω2R=2ω2r.由ωR=ω2r联立解得=,选项A正确,B错误;ma=μmg,所以=,选项C正确,D错误.
7.一杂技演员在圆筒状建筑物内表演飞车走壁,最后在直壁上沿水平方向做匀速圆周运动,下列说法中正确的是( AC )
A.车和演员作为一个整体受有重力、竖直壁对车的弹力和摩擦力的作用
B.车和演员做圆周运动所需要的向心力是静摩擦力
C.竖直壁对车的弹力提供向心力,且弹力随车速度的增大而增大
D.竖直壁对车的摩擦力将随车速增加而增加
8.如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动.则下列说法中正确的是( AB )
A.球A的线速度必定大于球B的线速度
B.球A的角速度必定小于球B的角速度
C.球A的运动周期必定小于球B的运动周期
D.球A对筒壁的压力必定大于球B对筒壁的压力
解析:
两球均贴着圆锥筒的内壁,在水平面内做匀速圆周运动,它们均受到重力和筒壁对它们的弹力作用,其合力必定在水平面内时刻指向圆心,如图所示.由图可知,筒壁对球的弹力为,对于A、B两球,因质量相等,θ角也相等,所以A、B两球受到筒壁的弹力大小也相等,由牛顿第三定律知,A、B两球对筒壁的压力大小也相等,D选项不正确.对球运用牛顿第二定律得mgcotθ=m=mω2r=m,球的线速度v=,角速度ω=,周期T=2π.由此可见,球的线速度随轨道半径的增大而增大,所以A球的线速度必定大于B球的线速度,A选项正确.球的角速度随半径的增大而减小,周期随半径的增大而增大,所以A球的角速度小于B球的角速度,A球的周期大于B球的周期,B选项正确,C选项不正确.
三、非选择题
9.如图所示,旋转木马被水平钢杆拴住绕转台的中心轴做匀速圆周运动.若相对两个木马间的杆长为6 m,木马质量为30 kg,骑木马的儿童质量为40 kg,当木马旋转的速度为6 m/s时,试问:
(1)此时木马和儿童的向心力分别是由哪个物体提供的?
(2)此时儿童受到的向心力是多大?
解析:(1)木马受骑在木马上的儿童对它的压力、重力和钢杆对它的作用力做匀速圆周运动.木马受到的向心力由水平钢杆提供;同理可得出儿童受到的向心力由木马提供.
(2)儿童所受向心力由木马提供且指向圆心,则
F向=m=40× N=480 N.
答案:(1)水平钢杆 木马 (2)480 N
10.有一种叫“飞椅”的游乐项目,示意图如图所示,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ.不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.
解析:设转盘转动的角速度为ω时,钢绳与竖直方向的夹角为θ,座椅到中心轴的距离即座椅转动半径为
R=r+Lsinθ.
设钢绳的拉力为FT,对座椅进行受力分析有
竖直方向FTcosθ=mg,水平方向F向=FTsinθ=mRω2,
联立以上各式得ω= .
答案:ω=
11.如图,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动.现测得转台半径R=0.5 m,离水平地面的高度H=0.8 m,物块平抛落地过程水平位移的大小s=0.4 m.设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10 m/s2.求:
(1)物块做平抛运动的初速度大小v0;
(2)物块与转台间的动摩擦因数μ.
解析:(1)物块做平抛运动,在竖直方向上有
H=gt2,①
在水平方向上有s=v0t,②
由①②式解得
v0=s,v0=1 m/s.③
(2)物块离开转台时,最大静摩擦力提供向心力,有
F′fm=m,④
Ffm=F′fm=μN=μmg,⑤
由③④⑤式解得μ=,μ=0.2.
答案:(1)1 m/s (2)0.2
