人教版数学九年级下册27.1.1 成比例线段课件(25张)
文档属性
| 名称 | 人教版数学九年级下册27.1.1 成比例线段课件(25张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 00:00:00 | ||
图片预览






文档简介
学习目标
理解并掌握线段的比、成比例线段的概念和相关组成元素.
理解并能灵活运用比例的基本性质解决问题.
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m、n;那么这两条线段的比就是两条线段的长度比.
其中,线段AB,CD分别叫做这个线段比的前项和后项.
1.线段的比
知识精讲
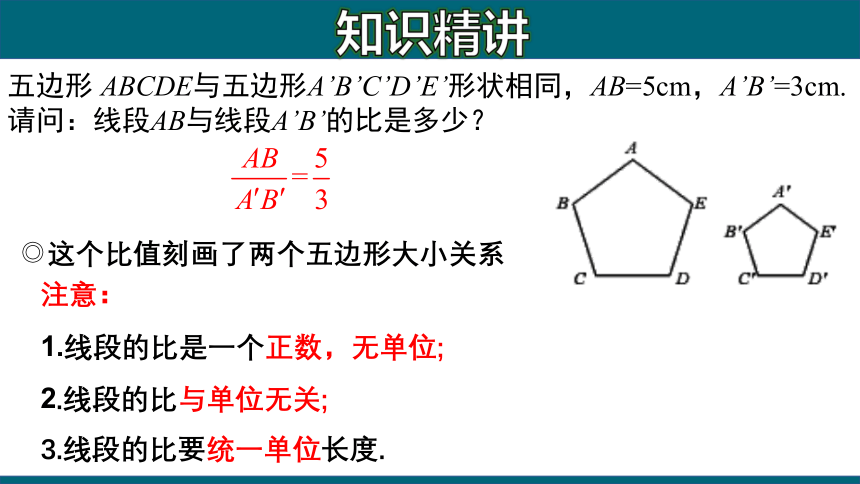
五边形 ABCDE与五边形A’B’C’D’E’形状相同,AB=5cm,A’B’=3cm.
请问:线段AB与线段A’B’的比是多少?
注意:
1.线段的比是一个正数,无单位;
2.线段的比与单位无关;
3.线段的比要统一单位长度.
◎这个比值刻画了两个五边形大小关系
知识精讲
1.已知教室黑板的长 a = 3.2 m,宽 b = 120 cm ,求 a:b.
∴a :b = 320 :120 = 8 :3
或:
2.一条线段的长度是另一条线段长度的 ,则这两条线段之比是?
∵a=3.2m=320cm
针对练习
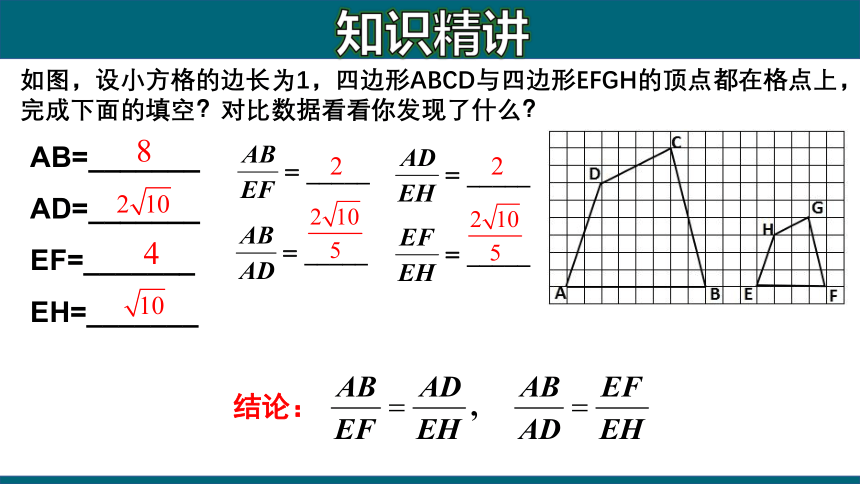
AB=_______
AD=_______
EF=_______
EH=_______
结论:
如图,设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,完成下面的填空?对比数据看看你发现了什么?
知识精讲
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即:
2.成比例线段的概念
那么这四条线段a,b,c,d叫做成比例线段,简称比例线段。
知识精讲
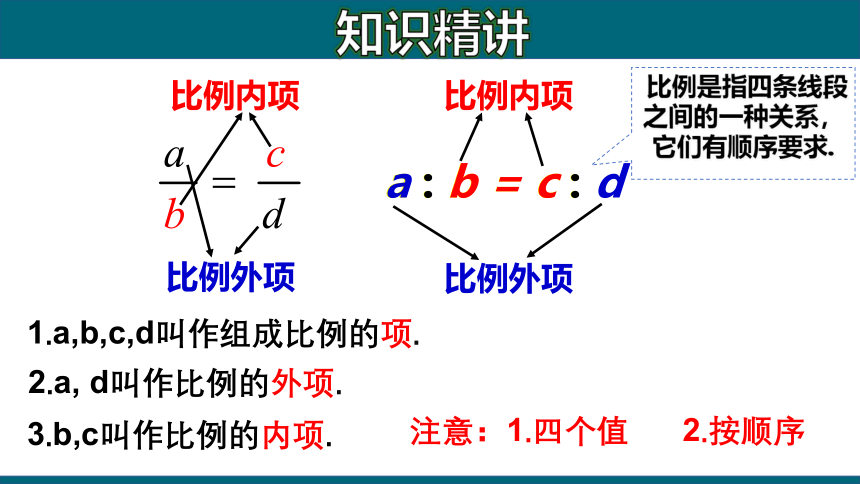
1.a,b,c,d叫作组成比例的项.
2.a, d叫作比例的外项.
3.b,c叫作比例的内项.
注意:1.四个值 2.按顺序
知识精讲
a : b = c :
比例内项
比例外项
比例是指四条线段之间的一种关系,它们有顺序要求.
a : b = c : d
比例内项
比例外项
例1判断下列线段a、b、c、d是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
∴ 线段a、b、c、d不是成比例线段。
解 (1) ∵ ,
,
∴
(2)a=2,b=
,c=
,d=
。
典例解析
例1判断下列线段a、b、c、d是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
(2)a=2,b=
,c=
,d=
。
(2) ∵ ,
,
∴
∴ 线段a、b、c、d是成比例线段。
典例解析
如何快速地判断线段是否成比例?
将线段从小到大(或从大到小)的顺序排列,计算第一和第二之比,第三和第四之比,看他们的比值是否相同.
判断下列线段是否是成比例线段:
(1)a=2cm,b=4cm,c=3m,d=6m;
(2)a=0.8,b=3,c=1,d=2.4.
所以a,c,d,b成比例线段.
针对练习
如果a,b,c,d四个数成比例,即 ,那么ad=bc吗?反过来如果ad=bc,那么a,b,c,d四个数成比例吗?(提示:你可以列举几组比例线段来验证一下。)
知识精讲
由ad=bc,得出 是有条件的,
即a,b,c,d都不等于0.
解:
左 右
右 左
右 左
左 右
你可以得到别的比例式吗?
知识精讲
1.如果
,那么ad=bc.
2.如果ad=bc(a、b、c、d都不等于0),那么 .
两外项之积=两内项之积.
左 右
右 左
交叉相乘积相等
右 左
左 右
3.比例的基本性质
知识精讲
1.a,b,c,d 是成比例线段,其中 a = 3 ,b = 2 ,c = 6 ,则d 的长____.
2.若x:6=(5+x):2,则x=____.
4
-7.5
针对练习
如果作为比例内项的两条线段是相等的,即 (或 a:b=b:c),那么线段b叫线段a,c的比例中项.。
特别地,
三种不同形式:
a:b=b:c
b2=ac
知识精讲
【点睛】线段比例中项与数的比例中项是两个不同的概念,前者是一个正数,而后者是一对互为相反数.
1.求下列线段a、b的比例中项.
(1)a=3,b=27;
2. 2和8两数的比例中项______.
针对练习
(2)
±4
达标检测
1.下列各组线段长度可组成成比例的是( )
A.2cm,3cm,4cm,1cm
B.6.5cm,1.5cm,2.5cm,4.5cm
C.1.1cm,2.2cm,3.3cm,4.4cm
D.2cm,2cm,1cm,4cm
D
2.在一张比例尺为1:20 000的地图上,量得A与B两地的距离是5 cm,则A,B两地实际距离为_________m.
1000
达标检测
3.已知线段a=4,b=8,则a、b的比例中项线段等于_____.
?
4.已知线段a、b、c、d是成比例线段,且a=2cm,b=0.6cm,c=4cm,那么d=______cm.
1.2
5.ab=mn,下列比例式中,不成立的是( )
A. B. C. D.
C
达标检测
6.如果 = = ,则式子 的值是________.
7.若x:y:z=3:4:7且2x-y+z=18,则x+2y-z=________.
【解析】解:∵x:y:z=3:4:7,
设x=3a,y=4a,z=7a,
∵2x-y+z=18,∴6a-4a+7a=18,
∴9a=18,∴a=2,
∴x=6,y=8,z=14,∴x+2y-z=6+16-14=8
?
3
8
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m、n;那么这两条线段的比就是两条线段的长度比。
其中,线段AB,CD分别叫做这个线段比的前项和后项。
1.线段的比
小结梳理
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即:
2.成比例线段的概念
那么这四条线段a,b,c,d叫做成比例线段,简称比例线段。
小结梳理
1.a,b,c,d叫作组成比例的项.
2.a, d叫作比例的外项.
3.b,c叫作比例的内项.
a : b = c :
比例内项
比例外项
比例是指四条线段之间的一种关系,它们有顺序要求.
a : b = c : d
比例内项
比例外项
小结梳理
1.如果
,那么ad=bc.
2.如果ad=bc(a、b、c、d都不等于0),那么 .
两外项之积=两内项之积。
左 右
右 左
交叉相乘积相等
右 左
左 右
3.比例的基本性质
知识精讲
理解并掌握线段的比、成比例线段的概念和相关组成元素.
理解并能灵活运用比例的基本性质解决问题.
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m、n;那么这两条线段的比就是两条线段的长度比.
其中,线段AB,CD分别叫做这个线段比的前项和后项.
1.线段的比
知识精讲
五边形 ABCDE与五边形A’B’C’D’E’形状相同,AB=5cm,A’B’=3cm.
请问:线段AB与线段A’B’的比是多少?
注意:
1.线段的比是一个正数,无单位;
2.线段的比与单位无关;
3.线段的比要统一单位长度.
◎这个比值刻画了两个五边形大小关系
知识精讲
1.已知教室黑板的长 a = 3.2 m,宽 b = 120 cm ,求 a:b.
∴a :b = 320 :120 = 8 :3
或:
2.一条线段的长度是另一条线段长度的 ,则这两条线段之比是?
∵a=3.2m=320cm
针对练习
AB=_______
AD=_______
EF=_______
EH=_______
结论:
如图,设小方格的边长为1,四边形ABCD与四边形EFGH的顶点都在格点上,完成下面的填空?对比数据看看你发现了什么?
知识精讲
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即:
2.成比例线段的概念
那么这四条线段a,b,c,d叫做成比例线段,简称比例线段。
知识精讲
1.a,b,c,d叫作组成比例的项.
2.a, d叫作比例的外项.
3.b,c叫作比例的内项.
注意:1.四个值 2.按顺序
知识精讲
a : b = c :
比例内项
比例外项
比例是指四条线段之间的一种关系,它们有顺序要求.
a : b = c : d
比例内项
比例外项
例1判断下列线段a、b、c、d是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
∴ 线段a、b、c、d不是成比例线段。
解 (1) ∵ ,
,
∴
(2)a=2,b=
,c=
,d=
。
典例解析
例1判断下列线段a、b、c、d是否是成比例线段:
(1)a=4,b=6,c=5,d=10;
(2)a=2,b=
,c=
,d=
。
(2) ∵ ,
,
∴
∴ 线段a、b、c、d是成比例线段。
典例解析
如何快速地判断线段是否成比例?
将线段从小到大(或从大到小)的顺序排列,计算第一和第二之比,第三和第四之比,看他们的比值是否相同.
判断下列线段是否是成比例线段:
(1)a=2cm,b=4cm,c=3m,d=6m;
(2)a=0.8,b=3,c=1,d=2.4.
所以a,c,d,b成比例线段.
针对练习
如果a,b,c,d四个数成比例,即 ,那么ad=bc吗?反过来如果ad=bc,那么a,b,c,d四个数成比例吗?(提示:你可以列举几组比例线段来验证一下。)
知识精讲
由ad=bc,得出 是有条件的,
即a,b,c,d都不等于0.
解:
左 右
右 左
右 左
左 右
你可以得到别的比例式吗?
知识精讲
1.如果
,那么ad=bc.
2.如果ad=bc(a、b、c、d都不等于0),那么 .
两外项之积=两内项之积.
左 右
右 左
交叉相乘积相等
右 左
左 右
3.比例的基本性质
知识精讲
1.a,b,c,d 是成比例线段,其中 a = 3 ,b = 2 ,c = 6 ,则d 的长____.
2.若x:6=(5+x):2,则x=____.
4
-7.5
针对练习
如果作为比例内项的两条线段是相等的,即 (或 a:b=b:c),那么线段b叫线段a,c的比例中项.。
特别地,
三种不同形式:
a:b=b:c
b2=ac
知识精讲
【点睛】线段比例中项与数的比例中项是两个不同的概念,前者是一个正数,而后者是一对互为相反数.
1.求下列线段a、b的比例中项.
(1)a=3,b=27;
2. 2和8两数的比例中项______.
针对练习
(2)
±4
达标检测
1.下列各组线段长度可组成成比例的是( )
A.2cm,3cm,4cm,1cm
B.6.5cm,1.5cm,2.5cm,4.5cm
C.1.1cm,2.2cm,3.3cm,4.4cm
D.2cm,2cm,1cm,4cm
D
2.在一张比例尺为1:20 000的地图上,量得A与B两地的距离是5 cm,则A,B两地实际距离为_________m.
1000
达标检测
3.已知线段a=4,b=8,则a、b的比例中项线段等于_____.
?
4.已知线段a、b、c、d是成比例线段,且a=2cm,b=0.6cm,c=4cm,那么d=______cm.
1.2
5.ab=mn,下列比例式中,不成立的是( )
A. B. C. D.
C
达标检测
6.如果 = = ,则式子 的值是________.
7.若x:y:z=3:4:7且2x-y+z=18,则x+2y-z=________.
【解析】解:∵x:y:z=3:4:7,
设x=3a,y=4a,z=7a,
∵2x-y+z=18,∴6a-4a+7a=18,
∴9a=18,∴a=2,
∴x=6,y=8,z=14,∴x+2y-z=6+16-14=8
?
3
8
如果选用同一个长度单位量得两条线段AB,CD的长度分别是m、n;那么这两条线段的比就是两条线段的长度比。
其中,线段AB,CD分别叫做这个线段比的前项和后项。
1.线段的比
小结梳理
四条线段a,b,c,d中,如果a与b的比等于c与d的比,即:
2.成比例线段的概念
那么这四条线段a,b,c,d叫做成比例线段,简称比例线段。
小结梳理
1.a,b,c,d叫作组成比例的项.
2.a, d叫作比例的外项.
3.b,c叫作比例的内项.
a : b = c :
比例内项
比例外项
比例是指四条线段之间的一种关系,它们有顺序要求.
a : b = c : d
比例内项
比例外项
小结梳理
1.如果
,那么ad=bc.
2.如果ad=bc(a、b、c、d都不等于0),那么 .
两外项之积=两内项之积。
左 右
右 左
交叉相乘积相等
右 左
左 右
3.比例的基本性质
知识精讲
