鲁科版_必修1_第2节 形变与弹力课件35张PPT
文档属性
| 名称 | 鲁科版_必修1_第2节 形变与弹力课件35张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-19 12:26:51 | ||
图片预览









文档简介
第二节
弹力
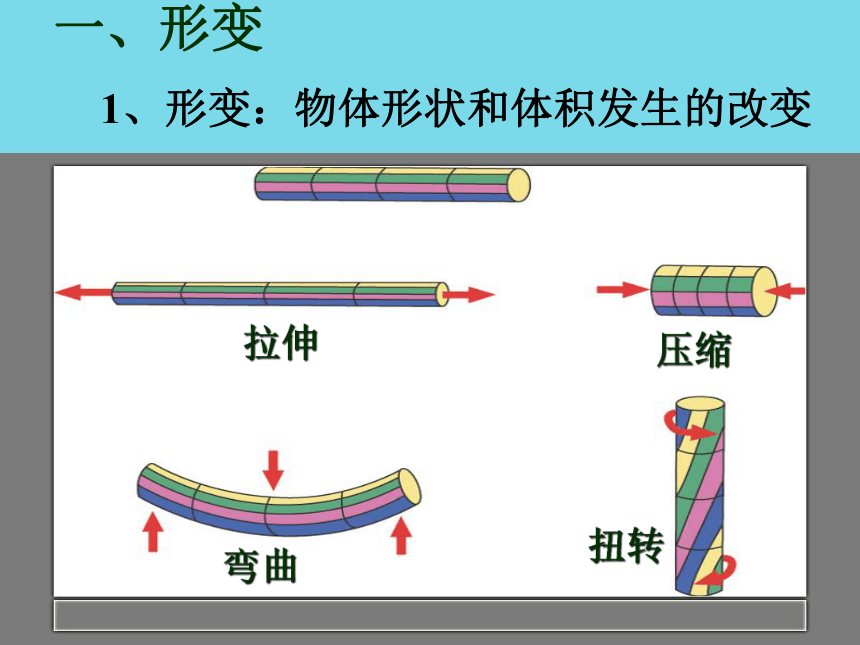
一、形变
1、形变:物体形状和体积发生的改变
拉伸
压缩
弯曲
扭转
2、形变的分类
1)按形变程度分
2)按可否恢复分
明显形变
微小形变
非弹性形变
弹性形变
弹性限度
如果形变过大,超过一定限度,即使撤去作用力,物体也不能完全恢复原来的形状,这个限度叫弹性限度
发生形变的物体在停止受力后,能恢复原状的形变称为弹性形变
桌子上放着本书,书和桌面有没有发生形变呢?
问题
都发生了微小形变
(微小形变的演示一)
手挤压玻璃瓶,观察水柱的变化。
二、弹力:
1、指发生弹性形变的物体由于要恢复原状,对与它接触的物体产生力的作用
物体1受到物体2的作用
物体1发生了形变
物体1对物体2产生了弹力
2、作用过程
3、弹力的施力物体与受力物体:
发生形变的物体
与施力物体接触,使它发生形变,并阻碍其恢复原状的物体
4、产生的条件 (产生原因)
(1)、物体间相互接触
(2)、物体发生弹性形变
接触力
(1)弹力的施力物体:
(2)弹力的受力物体:
弹力有无的判断
对于微小形变,用假设推理法
光滑水平面并排放着静止的木块A、B
假设A、B间有弹力
以B为研究对象,B受力:
G
N地
NA→B
B不可能静止,所以A、B间没有弹力
弹力有无的判断
判断球与斜面间有无弹力
假设球与斜面间有弹力
以球为研究对象,球受力:
G
FT
FN斜面→球
球不可能静止,所以球与斜面间没有弹力
弹力有无的判断
光滑球静止在水平地面
假设球与木块间有弹力
以球为研究对象,球受力:
G
FN
FN木块→球
球不可能静止,所以球与斜面间没有弹力
例:分析书放在桌面或倾斜木板上时,
书和木板所受的弹力
书
木板
书
板
FN1
FN1
FN2
FN2
三、弹力的方向:(压力、支持力方向)
各种接触面间的弹力方向判断:
曲面与平面接触
FN
FN
FN`
曲面与平面间弹力方向:
过接触点垂直平面指向受力物体
点与平面接触
FN
FN`
点与平面间弹力方向:
过接触点垂直平面指向受力物体
光滑斜面
A
B
FNA
FNB
点与曲面接触
点与曲面间弹力方向:
与过接触点的切面垂直并指向受力物体
N1
N2
半球形的碗
A
B
NA
NB
曲面与曲面接触
曲面与曲面间弹力方向:
与过接触点的公切面垂直并指向受力物体
半球形的碗
FN
A
B
N
NB对A
判断下列支持面对物体弹力的方向
点和曲面接触,弹力通过接触点垂直于切面
点和线接触,弹力通过接触点垂直于线
结论:压力、支持力方向总跟接触面垂直,指向受力物体
例:三个相同的支座上分别搁着三个质量和直径都相等的光滑圆球a,b,c,支点P、Q在同一水平面上,a球的重心O,位于球心,b球和c球的重心Ob和Oc分别位于球心的正上方和球心的正下方,如图所示,三球均处于平衡状态,支点P对a球的弹力为Na,对b球和c球的弹力分别为Nb和Nc则下列
说法正确的是( )
A.弹力Na、Nb、Nc的方向均由P 点指向球心
B.弹力Na、Nb、Nc的方向均由P 点指向重心
C.弹力Na、Nb、Nc的方向都竖直向上
A
b
?
Oa
?
?
?
?
Ob
Oc
P
P
P
Q
Q
Q
a
c
下列画出的光滑小球所受到的所有弹力示意图正确的有( )
例、画出下列光滑小球所受到的所有弹力。
丙
结论:绳上弹力方向总是沿着绳而指向绳子收缩的方向即指向施力物体
绳子的拉力也是弹力,那么绳子的拉力的方向如何呢?
轻绳的受力特点:
1、只能拉不能压;
2、轻绳的拉力一定沿绳方向;
3、同一根绳子张力处处相等。
轻绳受力特点
G
Ta
Tb
a
b
例如画出下列各物体所受弹力
A
A
分析下列物体所受的力
A
B
B
G
FT
A
G`
FT2
FT1
1
2
弹簧弹力方向又什么样的呢?
弹簧两端的弹力方向,与弹簧中心轴线重合,指向弹簧恢复原状方向.
轻杆受力特点
轻杆的含义:
不计质量不发生明显形变的杆
轻杆受力特点:
1、可拉可压;
2、杆所受的力不一定沿杆的方向;可能沿任意方向
四、弹力的作用点和大小
1、弹力的作用点:两物体接触处,在受力物体上。
2、对于同一物体,弹力大小同形变大小有关。
利用力的平衡来计算
利用牛顿第二定律
弹簧弹力大小计算—— 胡克定律
例1:两个物体A和B,质量分别为M和m,用跨过定滑轮的轻绳相连,A静止于水平地面上,如图所示.不计摩擦,A对绳的作用力的大小与地面对A的作用力的大小分别为多少?
FT=mg
FN=(M-m)g
例2:如图A、B两物体重力分别是GA=3N、GB=4N,A用悬绳挂在天花板上,B放在水平地面上,A、B间的轻弹簧的弹力F=2N,则绳中张力FT和B对地面的压力FN的可能值分别为( )
C、1N和6N
D、2N和5N
A、7N和0N
B、5N和2N
BC
例3:如图所示,A、B是质量均为m的两条磁铁,C为木块,水平放置。静止时B对A的弹力为F1,C对B的弹力为F2,则:( )
A、F1=mg,F2=2mg
B、F1>mg,F2=2mg
C、F1<mg,F2=2mg
D、F1>mg,F2>2mg
N
S
N
S
A
B
C
B
实验目的
1、探究弹力与 的定量关系。
2、学会利用图象研究两个物理量之间的关系的方法。
实验原理
1、如图所示,弹簧在下端悬挂钩码时会伸长,平衡时弹簧产生的弹力与 大小相等。
弹簧伸长
所挂钩码的重力
探究弹力与弹簧伸长量的关系
五、胡克定律:
2、用刻度尺测出弹簧在不同的钩码拉力下的伸长量x,建立坐标系,以纵坐标表示弹力大小F,以横坐标表示弹簧的伸长量x,在坐标系中描写实验所测得的各组(x,F)对应的点,用 的曲线连接起来,根据实验所得的图线,就可探知弹力大小与伸长量间的关系。
平滑
结论:胡克定律
1、内容:
弹簧发生弹性形变时,弹力的大小跟弹簧伸长(或缩短)的长度x成正比。
2、公式:
F = k x
其中:k——弹簧的劲度系数 (与弹簧的丝的粗细、材料、弹簧的直径、绕法和长度等量有关)
单位:牛每米, 符号N/m
x——弹簧伸长(或缩短)的长度
例:如图所示,为一轻质弹簧的长度L和弹力F大小的关系,试由图线确定:
(1)弹簧的原长;
(2)弹簧的劲度系数;
(3)弹簧长为0.2m时弹力的大小.
(1)10cm
(2)200N/m (3)20N
练习:两根长均为20cm的弹簧,劲度系数分别为k1=200N/m,k2=100N/m,弹簧k2固定在A上,弹簧k1固定在A、B上,B放在水平地面上,弹簧竖直,如图所示。已知A、B所受的重力都是4N,今在k2的端点P施加一个竖直向上的力,缓慢地向上拉,当P点向上升距离为多少 时,
B和地面恰好接触而没有作用力。
弹簧自重不计。
12cm
小结
一、弹力产生条件:
① 直接接触
② 发生弹性形变
二、弹力方向
1、压力和支持力:
方向都垂直于接触面指向被压或被支持的物体(受力物体)。
2、轻绳的弹力(又叫拉力或张力):
绳的拉力沿着绳指向绳 收缩的方向(即指向施力物体)
小结
三、弹力大小:
1、弹簧弹力:胡克定律F = k x
2、其它弹力:由物体受其它力和运动状态求解(根据平衡条件或牛顿定律计算)
弹力
一、形变
1、形变:物体形状和体积发生的改变
拉伸
压缩
弯曲
扭转
2、形变的分类
1)按形变程度分
2)按可否恢复分
明显形变
微小形变
非弹性形变
弹性形变
弹性限度
如果形变过大,超过一定限度,即使撤去作用力,物体也不能完全恢复原来的形状,这个限度叫弹性限度
发生形变的物体在停止受力后,能恢复原状的形变称为弹性形变
桌子上放着本书,书和桌面有没有发生形变呢?
问题
都发生了微小形变
(微小形变的演示一)
手挤压玻璃瓶,观察水柱的变化。
二、弹力:
1、指发生弹性形变的物体由于要恢复原状,对与它接触的物体产生力的作用
物体1受到物体2的作用
物体1发生了形变
物体1对物体2产生了弹力
2、作用过程
3、弹力的施力物体与受力物体:
发生形变的物体
与施力物体接触,使它发生形变,并阻碍其恢复原状的物体
4、产生的条件 (产生原因)
(1)、物体间相互接触
(2)、物体发生弹性形变
接触力
(1)弹力的施力物体:
(2)弹力的受力物体:
弹力有无的判断
对于微小形变,用假设推理法
光滑水平面并排放着静止的木块A、B
假设A、B间有弹力
以B为研究对象,B受力:
G
N地
NA→B
B不可能静止,所以A、B间没有弹力
弹力有无的判断
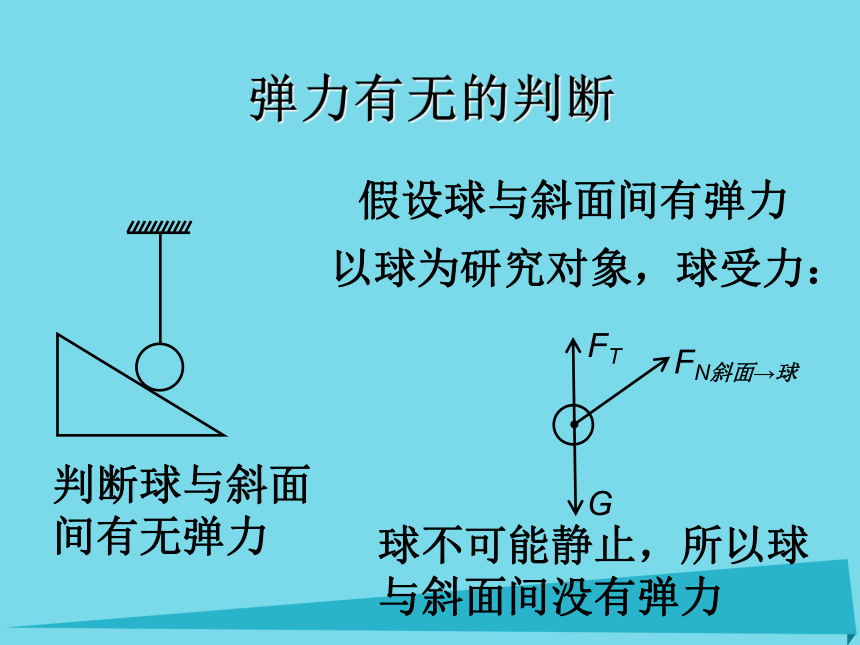
判断球与斜面间有无弹力
假设球与斜面间有弹力
以球为研究对象,球受力:
G
FT
FN斜面→球
球不可能静止,所以球与斜面间没有弹力
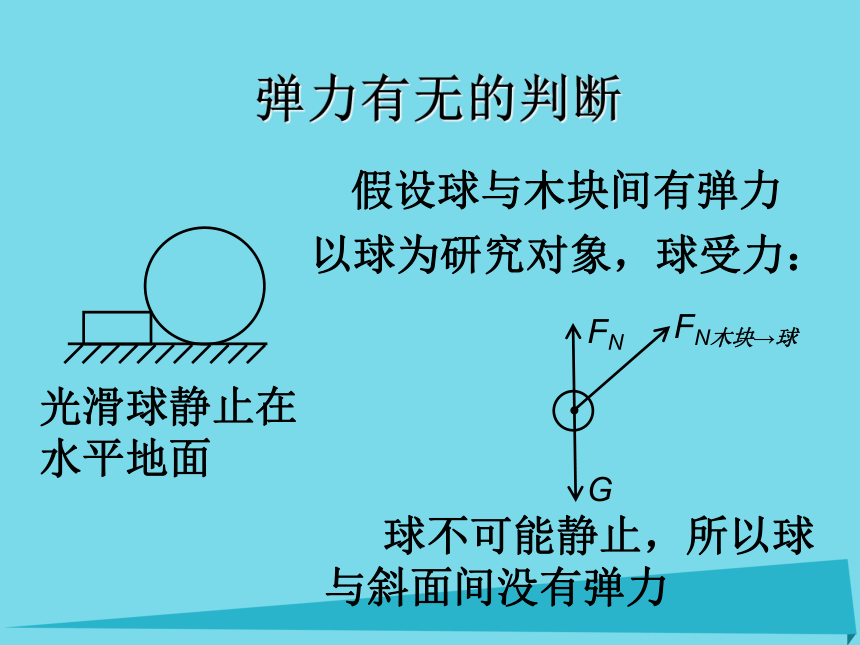
弹力有无的判断
光滑球静止在水平地面
假设球与木块间有弹力
以球为研究对象,球受力:
G
FN
FN木块→球
球不可能静止,所以球与斜面间没有弹力
例:分析书放在桌面或倾斜木板上时,
书和木板所受的弹力
书
木板
书
板
FN1
FN1
FN2
FN2
三、弹力的方向:(压力、支持力方向)
各种接触面间的弹力方向判断:
曲面与平面接触
FN
FN
FN`
曲面与平面间弹力方向:
过接触点垂直平面指向受力物体
点与平面接触
FN
FN`
点与平面间弹力方向:
过接触点垂直平面指向受力物体
光滑斜面
A
B
FNA
FNB
点与曲面接触
点与曲面间弹力方向:
与过接触点的切面垂直并指向受力物体
N1
N2
半球形的碗
A
B
NA
NB
曲面与曲面接触
曲面与曲面间弹力方向:
与过接触点的公切面垂直并指向受力物体
半球形的碗
FN
A
B
N
NB对A
判断下列支持面对物体弹力的方向
点和曲面接触,弹力通过接触点垂直于切面
点和线接触,弹力通过接触点垂直于线
结论:压力、支持力方向总跟接触面垂直,指向受力物体
例:三个相同的支座上分别搁着三个质量和直径都相等的光滑圆球a,b,c,支点P、Q在同一水平面上,a球的重心O,位于球心,b球和c球的重心Ob和Oc分别位于球心的正上方和球心的正下方,如图所示,三球均处于平衡状态,支点P对a球的弹力为Na,对b球和c球的弹力分别为Nb和Nc则下列
说法正确的是( )
A.弹力Na、Nb、Nc的方向均由P 点指向球心
B.弹力Na、Nb、Nc的方向均由P 点指向重心
C.弹力Na、Nb、Nc的方向都竖直向上
A
b
?
Oa
?
?
?
?
Ob
Oc
P
P
P
Q
Q
Q
a
c
下列画出的光滑小球所受到的所有弹力示意图正确的有( )
例、画出下列光滑小球所受到的所有弹力。
丙
结论:绳上弹力方向总是沿着绳而指向绳子收缩的方向即指向施力物体
绳子的拉力也是弹力,那么绳子的拉力的方向如何呢?
轻绳的受力特点:
1、只能拉不能压;
2、轻绳的拉力一定沿绳方向;
3、同一根绳子张力处处相等。
轻绳受力特点
G
Ta
Tb
a
b
例如画出下列各物体所受弹力
A
A
分析下列物体所受的力
A
B
B
G
FT
A
G`
FT2
FT1
1
2
弹簧弹力方向又什么样的呢?
弹簧两端的弹力方向,与弹簧中心轴线重合,指向弹簧恢复原状方向.
轻杆受力特点
轻杆的含义:
不计质量不发生明显形变的杆
轻杆受力特点:
1、可拉可压;
2、杆所受的力不一定沿杆的方向;可能沿任意方向
四、弹力的作用点和大小
1、弹力的作用点:两物体接触处,在受力物体上。
2、对于同一物体,弹力大小同形变大小有关。
利用力的平衡来计算
利用牛顿第二定律
弹簧弹力大小计算—— 胡克定律
例1:两个物体A和B,质量分别为M和m,用跨过定滑轮的轻绳相连,A静止于水平地面上,如图所示.不计摩擦,A对绳的作用力的大小与地面对A的作用力的大小分别为多少?
FT=mg
FN=(M-m)g
例2:如图A、B两物体重力分别是GA=3N、GB=4N,A用悬绳挂在天花板上,B放在水平地面上,A、B间的轻弹簧的弹力F=2N,则绳中张力FT和B对地面的压力FN的可能值分别为( )
C、1N和6N
D、2N和5N
A、7N和0N
B、5N和2N
BC
例3:如图所示,A、B是质量均为m的两条磁铁,C为木块,水平放置。静止时B对A的弹力为F1,C对B的弹力为F2,则:( )
A、F1=mg,F2=2mg
B、F1>mg,F2=2mg
C、F1<mg,F2=2mg
D、F1>mg,F2>2mg
N
S
N
S
A
B
C
B
实验目的
1、探究弹力与 的定量关系。
2、学会利用图象研究两个物理量之间的关系的方法。
实验原理
1、如图所示,弹簧在下端悬挂钩码时会伸长,平衡时弹簧产生的弹力与 大小相等。
弹簧伸长
所挂钩码的重力
探究弹力与弹簧伸长量的关系
五、胡克定律:
2、用刻度尺测出弹簧在不同的钩码拉力下的伸长量x,建立坐标系,以纵坐标表示弹力大小F,以横坐标表示弹簧的伸长量x,在坐标系中描写实验所测得的各组(x,F)对应的点,用 的曲线连接起来,根据实验所得的图线,就可探知弹力大小与伸长量间的关系。
平滑
结论:胡克定律
1、内容:
弹簧发生弹性形变时,弹力的大小跟弹簧伸长(或缩短)的长度x成正比。
2、公式:
F = k x
其中:k——弹簧的劲度系数 (与弹簧的丝的粗细、材料、弹簧的直径、绕法和长度等量有关)
单位:牛每米, 符号N/m
x——弹簧伸长(或缩短)的长度
例:如图所示,为一轻质弹簧的长度L和弹力F大小的关系,试由图线确定:
(1)弹簧的原长;
(2)弹簧的劲度系数;
(3)弹簧长为0.2m时弹力的大小.
(1)10cm
(2)200N/m (3)20N
练习:两根长均为20cm的弹簧,劲度系数分别为k1=200N/m,k2=100N/m,弹簧k2固定在A上,弹簧k1固定在A、B上,B放在水平地面上,弹簧竖直,如图所示。已知A、B所受的重力都是4N,今在k2的端点P施加一个竖直向上的力,缓慢地向上拉,当P点向上升距离为多少 时,
B和地面恰好接触而没有作用力。
弹簧自重不计。
12cm
小结
一、弹力产生条件:
① 直接接触
② 发生弹性形变
二、弹力方向
1、压力和支持力:
方向都垂直于接触面指向被压或被支持的物体(受力物体)。
2、轻绳的弹力(又叫拉力或张力):
绳的拉力沿着绳指向绳 收缩的方向(即指向施力物体)
小结
三、弹力大小:
1、弹簧弹力:胡克定律F = k x
2、其它弹力:由物体受其它力和运动状态求解(根据平衡条件或牛顿定律计算)
同课章节目录
- 第1章 绪论
- 物理学与自然规律
- 物理学与社会发展
- 怎样学习物理学
- 高中物理教材特点
- 第2章 运动的描述
- 导入 认识运动
- 第1节 运动、空间和时间
- 第2节 质点和位移
- 第3节 速度和加速度
- 第3章 匀变速直线运动的研究
- 导入 速度的变化
- 第1节 匀变速直线运动的规律
- 第2节 匀变速直线运动的实验探究
- 第3节 匀变速直线运动实例-自由落体运动
- 第4章 相互作用
- 导入 奇特的力现象
- 第1节 重力与重心
- 第2节 形变与弹力
- 第3节 摩擦力
- 第5章 力与平衡
- 导入 感悟平衡之美
- 第1节 力的合成
- 第2节 力的分解
- 第3节 力的平衡
- 第4节 平衡条件的应用
- 第6章 力与运动
- 导入 跨越时空的对话
- 第1节 牛顿第一定律
- 第2节 牛顿第二定律
- 第3节 牛顿第三定律
- 第4节 超重与失重
- 本章复习与测试
