相似三角形中的辅助线
图片预览


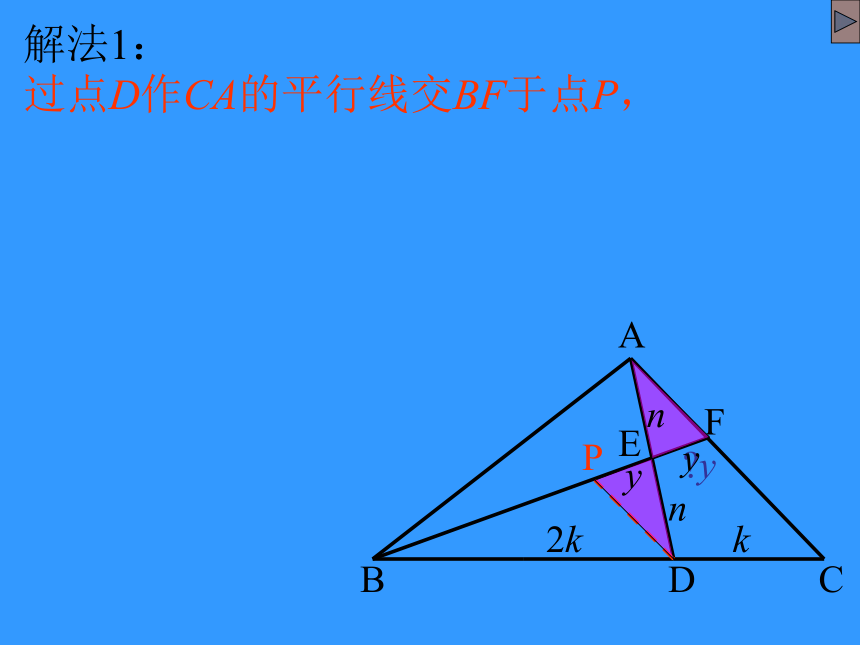
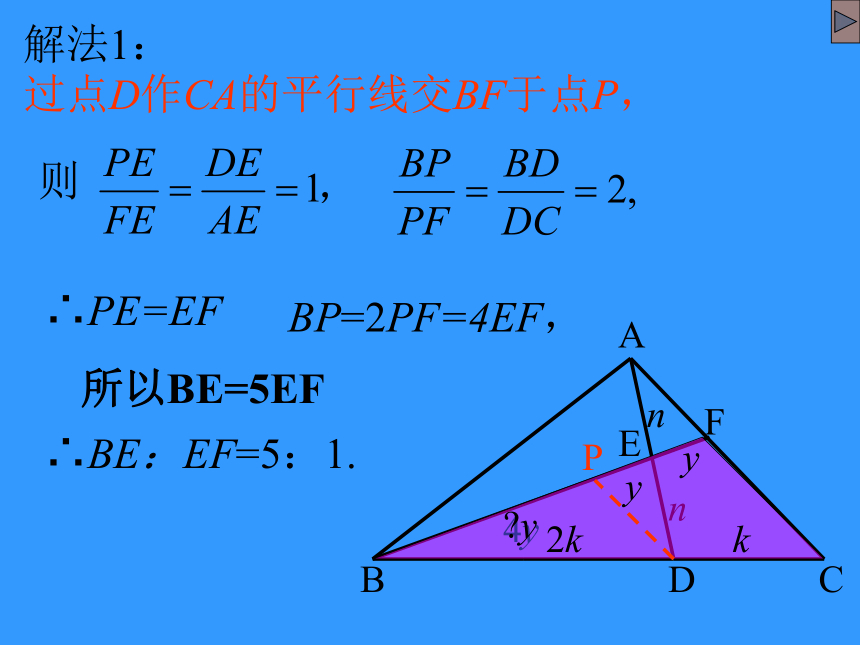
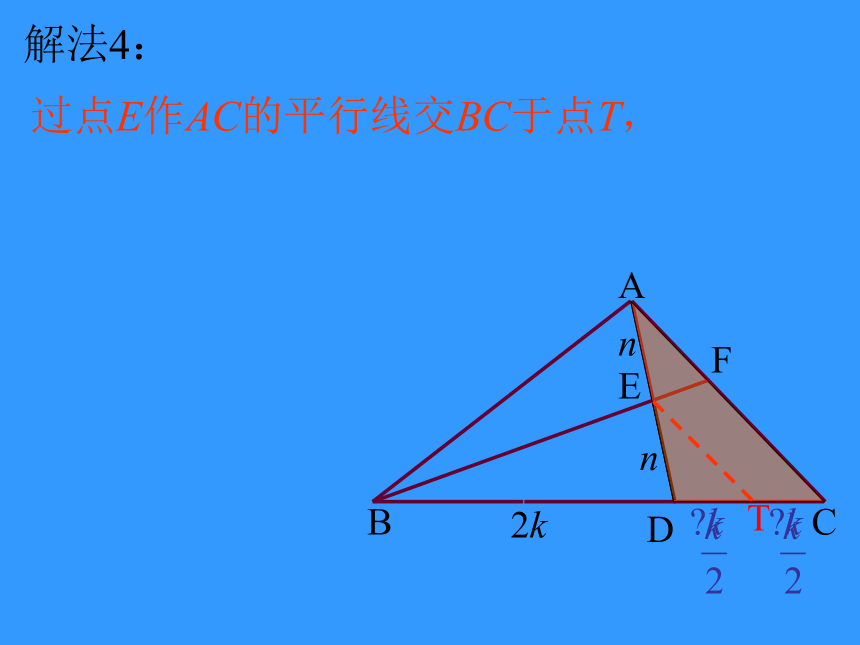
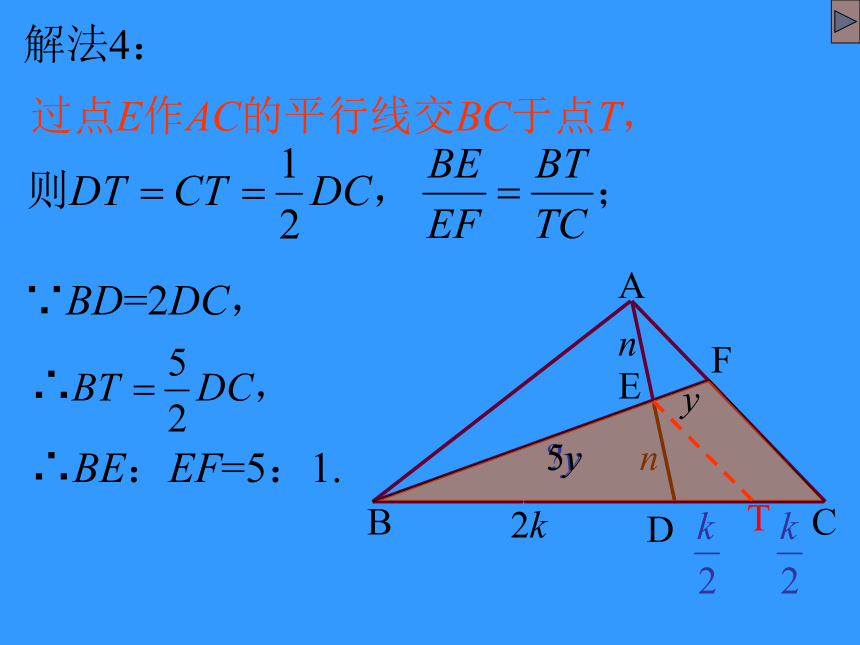
文档简介
(共50张PPT)
相似三角形中的辅助线
在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或得出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。主要的辅助线有以下几种:
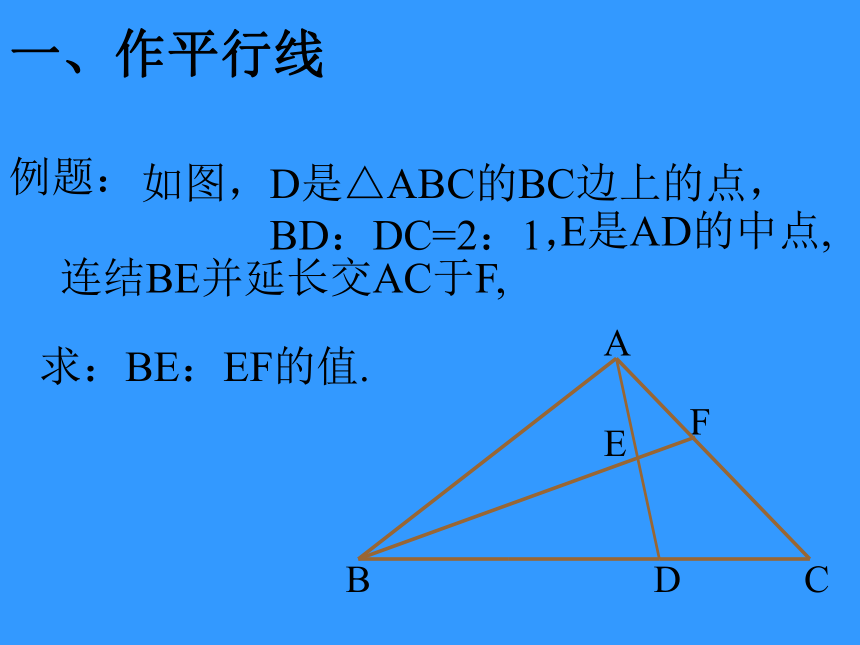
例题:
如图,D是△ABC的BC边上的点,
BD:DC=2:1,
求:BE:EF的值.
D
A
B
C
E
F
E是AD的中点,
连结BE并延长交AC于F,
一、作平行线
D
A
B
C
E
F
n
2k
k
解法1:
过点D作CA的平行线交BF于点P,
P
y
y
n
y
D
A
B
C
E
F
n
解法1:
过点D作CA的平行线交BF于点P,
P
n
2k
k
y
y
4y
y
∴BE:EF=5:1.
则
∴PE=EF
BP=2PF=4EF,
所以BE=5EF
D
A
B
C
E
F
n
n
2k
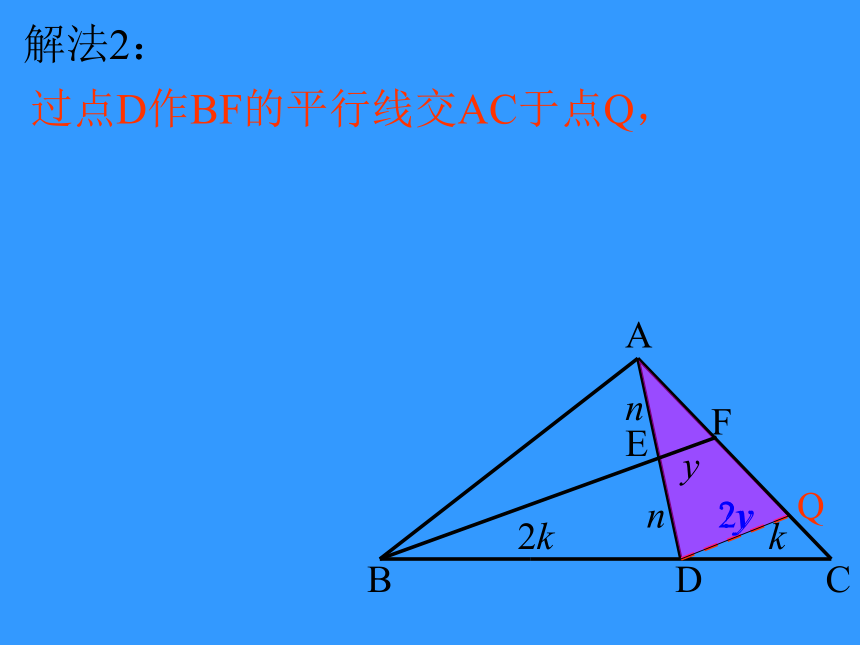
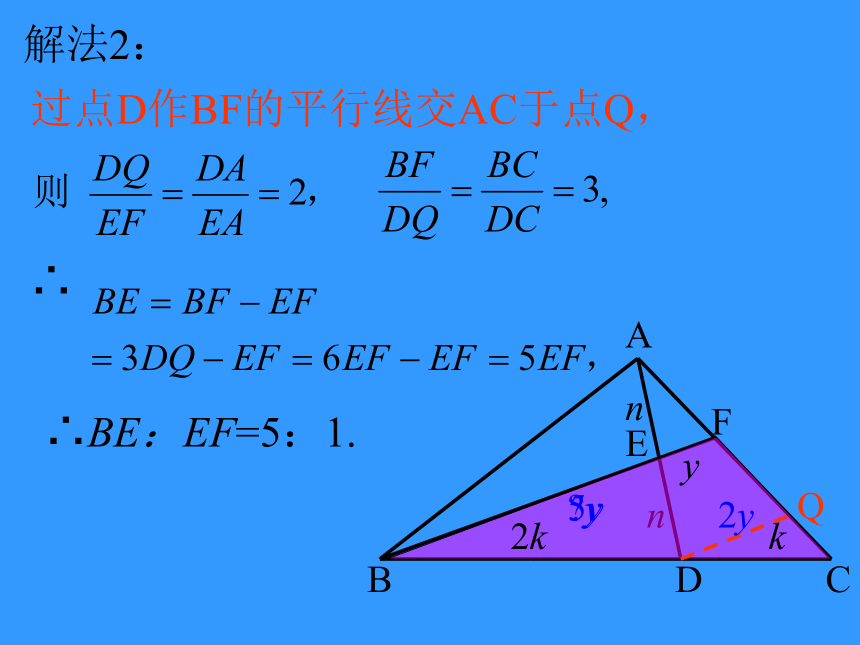
解法2:
过点D作BF的平行线交AC于点Q,
y
k
Q
y
2y
D
A
B
C
E
F
n
n
解法2:
过点D作BF的平行线交AC于点Q,
Q
2k
k
y
2y
5y
y
∴BE:EF=5:1.
∴
D
A
B
C
E
F
2k
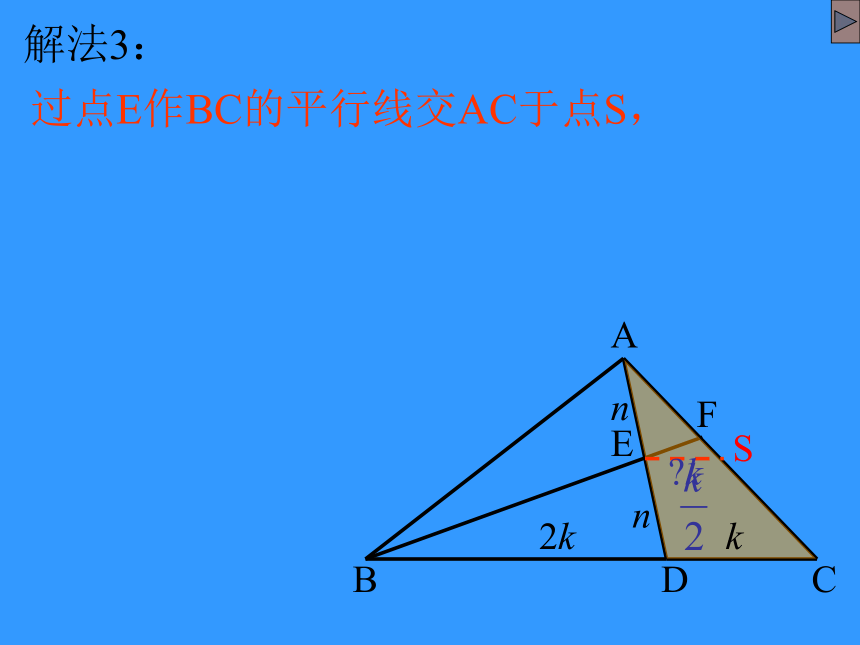
解法3:
过点E作BC的平行线交AC于点S,
S
n
n
k
k
D
A
B
C
E
F
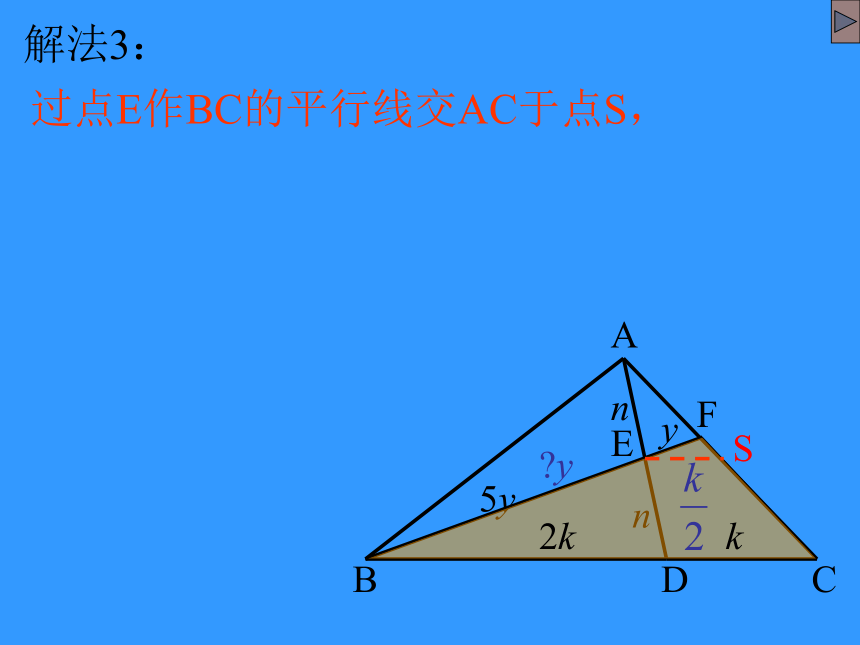
解法3:
过点E作BC的平行线交AC于点S,
S
n
n
y
5y
y
2k
k
D
A
B
C
E
F
n
n
2k
解法4:
过点E作AC的平行线交BC于点T,
T
k
k
D
A
B
C
E
F
n
n
2k
解法4:
过点E作AC的平行线交BC于点T,
T
y
y
5y
∵BD=2DC,
∴
∴BE:EF=5:1.
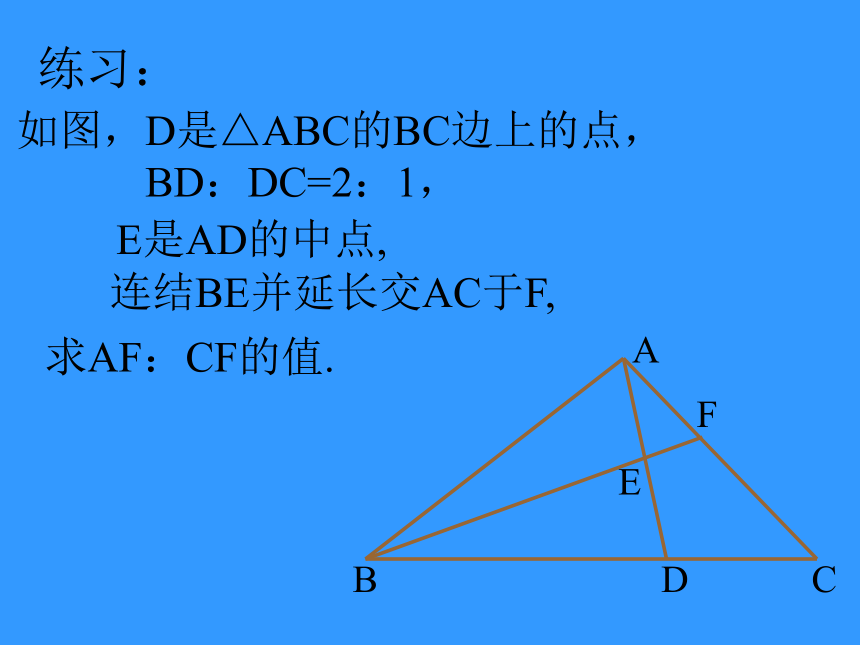
练习:
如图,D是△ABC的BC边上的点,
BD:DC=2:1,
求AF:CF的值.
D
A
B
C
E
F
E是AD的中点,
连结BE并延长交AC于F,
D
A
B
C
E
F
解法1:
过点D作CA的平行线交BF于点P,
P
n
n
2x
2x
2k
k
3x
AF:CF=2:3.
D
A
B
C
E
F
解法2:
过点D作BF的平行线交AC于点Q,
Q
n
n
2x
2x
2k
k
x
AF:CF=2:3.
D
A
B
C
E
F
解法3:
过点E作BC的平行线交AC于点S,
S
n
n
h
2h
4h
y
5y
4y
AF:CF=2:3.
D
A
B
C
E
F
解法4:
过点E作AC的平行线交BC于点T,
T
n
n
h
h
4h
5y
6y
4y
AF:CF=2:3.
作平行线
例1. 如图,的AB边和AC边上各取一点D和E,且使AD=AE,DE延长线与BC延长线相交于F,求证:
证明:过点C作CG//FD交AB于G
小结:本题关键在于AD=AE这个条件怎样使用。由这道题还可以增加一种证明线段相等的方法:相似、成比例。
例2. 如图,△ABC中,AB分析:证明等积式问题常常化为比例式,再通过相似三角形对应边成比例来证明。不相似,因而要通过两组三角形相似,运用中间比代换得到,为构造相似三角形,需添加平行线。
方法一:过E作EM//AB,交BC于点M,则△EMC∽△ABC(两角对应相等,两三角形相似)。
方法二:如图,过D作DN//EC交BC于N
1、在△ABC中,D为AC上的一点,E为CB延长线上的一点,BE=AD,DE交AB于F。
求证:EF×BC=AC×DF
1、证明:
过D作DG∥BC交AB于G,
则△DFG和△EFB相似,∴
∵BE=AD,∴
①由DG∥BC可得△ADG和△ACB相似,
∴
∴
由①②得,
∴EF×BC=AC×DF
①
②
1、已知点D是BC的中点,过D点的直线交AC
于E,交BA的延长线于F,求证:
E
F
B
C
A
D
利用比例式够造平行线,通过中间比得结论
利用中点”倍长中线”的思想平移线段EC,使得所得四条线段分别构成两个三角形
已知:在等腰三角形ABC中,AB=AC,BD是高,求证:BC2=2AC·CD
A
B
C
D
本题的 重点在于如何解决“2”倍的 问题;让它归属一条线段,找到这一线段2倍是哪一线段。
已知:从直角三角形ABC的 直角顶点A向斜边BC引垂线,垂足为D,边AC的中点为E,直线ED与边AB的延长线交于F,
求证:AB:AC=DF:AF
F
E
A
B
C
D
利用前两题的 思想方法,借助中点构造中位线,利用平行与2倍关系的 结论,证明所得结论
找到后以比例式所在三角形与哪个三角形相似
1、如图,△ABC中,AD是BC边上中线,E是AC上一点,连接ED且交AB的延长线于F点.
求证:AE:EC=AF:BF
A
C
B
F
D
E
注意观察图形的 特殊性,有些像全等中,旋转的基本图形,因此可以没有相互关系的 成比例的四条线段转化为成比例的四条线段(通过全等找相等的 线段)
关键是要把成比例线段放在两个三角形中
2、如图,平行四边形ABCD中,E为AB边中点,点F在AD边上,且AF:FD=1:2,EF交AC于G,求 的值
.
G
E
D
A
B
C
F
1、在 ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F,求证:BP2=PE·PF
P
E
A
B
C
F
D
在同一直线上的三条线段成比例,可以通过中间比转化,
也可以通过线段相等,把共线的线段转化为两个三角形中的 线段,通过相似证明。
另外在证明等积式时要先转化为比例式观察相似关系,有利于证明
1、如图,梯形ABCD中,AD∥BC,AC、BD交于O点,BA、CD的延长线交于E点,连结EO并延长分别交AD、BC于N、M
求证: BM=CM
j
A
D
B
C
E
M
N
O
1、如图,AD是∠BAC的平分线,EF是AD的垂直平分线,求证:ED2=EB·EC
F
A
B
C
E
D
2、如图,在矩形ABCD中,E是AD的中点,EF⊥EC交AB于F,连接FC(AB>AE),
求证: AEF∽ ECF
E
C
D
B
A
F
2、已知,在 ABC中,若AB=BC,∠B=90 ,AD为BC边的中线,过B作直线BP⊥AD于P交AC于E,求证:AE=2EC ;∠AEB= ∠CED.
D
A
B
C
E
二、作垂线
3. 如图从 ABCD顶点C向AB和AD的延长线引垂线CE和CF,垂足分别为E、F,求证:
证明:过B作BM⊥AC于M,过D作DN⊥AC于N
∴
∽
∴
∴
(1)
∽
∴
∴
(2)
又
∴ AN=CM
又
(1)+(2)
∴
2、中,,AC=BC,P是AB上一点,Q是PC上一点(不是中点),MN过Q且MN⊥CP,交AC、BC于M、N,求证:
2、证明:
过P作PE⊥AC于E,PF⊥CB于F,
则CEPF为矩形∴ PF
EC ∵
∴
∽
∴
∵ EC=PF ∴
(1) 在
和
中:CP⊥MN于Q ∴
又 ∵
∴
∴
∽
∴
即
由(1)(2)得
(2)
三、作延长线
例5. 如图,在梯形ABCD中,AD∥BC,若∠BCD的平分线CH⊥AB于点H,BH=3AH,且四边形AHCD的面积为21,求△HBC的面积。
分析:因为问题涉及四边形AHCD,所以可构造相似三角形。把问题转化为相似三角形的面积比而加以解决。
解:延长BA、CD交于点P
∵CH⊥AB,CD平分∠BCD
∴CB=CP,且BH=PH
∵BH=3AH
∴PA:AB=1:2
∴PA:PB=1:3
∵AD∥BC
∴△PAD∽△PBC
例6. 如图,RtABC中,CD为斜边AB上的高,E为CD的中点,AE的延长线交BC于F,FGAB于G,求证:FG=CFBF
解析:欲证式即 由“三点定形”,ΔBFG
与ΔCFG会相似吗?显然不可能。(因为ΔBFG为RtΔ),但由E为CD的中点,∴可设法构造一个与ΔBFG相似的三角形来求解。
不妨延长GF与AC的延长线交于H
则
又ED=EC ∴FG=FH 又易证RtΔCFH∽RtΔGFB
∴FG·FH=CF·BF
∵FG=FH ∴FG2=CF·BF
四、作中线
例7 如图,中,AB⊥AC,AE⊥BC于E,D在AC边上,若BD=DC=EC=1,求AC。
解:取BC的中点M,连AM
∵ AB⊥AC ∴ AM=CM
∴ ∠1=∠C 又 BD=DC
∴
∴
∽
∴
又 DC=1 MC=
BC
∴
(1)
又
∽
又 ∵ EC=1 ∴
由(1)(2)得,
∴
(2)
∴
小结:利用等腰三角形有公共底角,则这两个三角形相似,取BC中点M,构造
与
相似是解题关键
3、
理由?(用三种解法)
方法一:如图(1),设BC中点为E,连接AE。
方法二:如图(2),在DA上截取DE=DC
在△BED与△BCD中,
方法三:如图(3),过B作BE⊥BC于B,交CA的延长线于E。
我有哪些收获呢?
与大家共分享!
相似三角形中的辅助线
在添加辅助线时,所添加的辅助线往往能够构造出一组或多组相似三角形,或得到成比例的线段或得出等角,等边,从而为证明三角形相似或进行相关的计算找到等量关系。主要的辅助线有以下几种:
例题:
如图,D是△ABC的BC边上的点,
BD:DC=2:1,
求:BE:EF的值.
D
A
B
C
E
F
E是AD的中点,
连结BE并延长交AC于F,
一、作平行线
D
A
B
C
E
F
n
2k
k
解法1:
过点D作CA的平行线交BF于点P,
P
y
y
n
y
D
A
B
C
E
F
n
解法1:
过点D作CA的平行线交BF于点P,
P
n
2k
k
y
y
4y
y
∴BE:EF=5:1.
则
∴PE=EF
BP=2PF=4EF,
所以BE=5EF
D
A
B
C
E
F
n
n
2k
解法2:
过点D作BF的平行线交AC于点Q,
y
k
Q
y
2y
D
A
B
C
E
F
n
n
解法2:
过点D作BF的平行线交AC于点Q,
Q
2k
k
y
2y
5y
y
∴BE:EF=5:1.
∴
D
A
B
C
E
F
2k
解法3:
过点E作BC的平行线交AC于点S,
S
n
n
k
k
D
A
B
C
E
F
解法3:
过点E作BC的平行线交AC于点S,
S
n
n
y
5y
y
2k
k
D
A
B
C
E
F
n
n
2k
解法4:
过点E作AC的平行线交BC于点T,
T
k
k
D
A
B
C
E
F
n
n
2k
解法4:
过点E作AC的平行线交BC于点T,
T
y
y
5y
∵BD=2DC,
∴
∴BE:EF=5:1.
练习:
如图,D是△ABC的BC边上的点,
BD:DC=2:1,
求AF:CF的值.
D
A
B
C
E
F
E是AD的中点,
连结BE并延长交AC于F,
D
A
B
C
E
F
解法1:
过点D作CA的平行线交BF于点P,
P
n
n
2x
2x
2k
k
3x
AF:CF=2:3.
D
A
B
C
E
F
解法2:
过点D作BF的平行线交AC于点Q,
Q
n
n
2x
2x
2k
k
x
AF:CF=2:3.
D
A
B
C
E
F
解法3:
过点E作BC的平行线交AC于点S,
S
n
n
h
2h
4h
y
5y
4y
AF:CF=2:3.
D
A
B
C
E
F
解法4:
过点E作AC的平行线交BC于点T,
T
n
n
h
h
4h
5y
6y
4y
AF:CF=2:3.
作平行线
例1. 如图,的AB边和AC边上各取一点D和E,且使AD=AE,DE延长线与BC延长线相交于F,求证:
证明:过点C作CG//FD交AB于G
小结:本题关键在于AD=AE这个条件怎样使用。由这道题还可以增加一种证明线段相等的方法:相似、成比例。
例2. 如图,△ABC中,AB
方法一:过E作EM//AB,交BC于点M,则△EMC∽△ABC(两角对应相等,两三角形相似)。
方法二:如图,过D作DN//EC交BC于N
1、在△ABC中,D为AC上的一点,E为CB延长线上的一点,BE=AD,DE交AB于F。
求证:EF×BC=AC×DF
1、证明:
过D作DG∥BC交AB于G,
则△DFG和△EFB相似,∴
∵BE=AD,∴
①由DG∥BC可得△ADG和△ACB相似,
∴
∴
由①②得,
∴EF×BC=AC×DF
①
②
1、已知点D是BC的中点,过D点的直线交AC
于E,交BA的延长线于F,求证:
E
F
B
C
A
D
利用比例式够造平行线,通过中间比得结论
利用中点”倍长中线”的思想平移线段EC,使得所得四条线段分别构成两个三角形
已知:在等腰三角形ABC中,AB=AC,BD是高,求证:BC2=2AC·CD
A
B
C
D
本题的 重点在于如何解决“2”倍的 问题;让它归属一条线段,找到这一线段2倍是哪一线段。
已知:从直角三角形ABC的 直角顶点A向斜边BC引垂线,垂足为D,边AC的中点为E,直线ED与边AB的延长线交于F,
求证:AB:AC=DF:AF
F
E
A
B
C
D
利用前两题的 思想方法,借助中点构造中位线,利用平行与2倍关系的 结论,证明所得结论
找到后以比例式所在三角形与哪个三角形相似
1、如图,△ABC中,AD是BC边上中线,E是AC上一点,连接ED且交AB的延长线于F点.
求证:AE:EC=AF:BF
A
C
B
F
D
E
注意观察图形的 特殊性,有些像全等中,旋转的基本图形,因此可以没有相互关系的 成比例的四条线段转化为成比例的四条线段(通过全等找相等的 线段)
关键是要把成比例线段放在两个三角形中
2、如图,平行四边形ABCD中,E为AB边中点,点F在AD边上,且AF:FD=1:2,EF交AC于G,求 的值
.
G
E
D
A
B
C
F
1、在 ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F,求证:BP2=PE·PF
P
E
A
B
C
F
D
在同一直线上的三条线段成比例,可以通过中间比转化,
也可以通过线段相等,把共线的线段转化为两个三角形中的 线段,通过相似证明。
另外在证明等积式时要先转化为比例式观察相似关系,有利于证明
1、如图,梯形ABCD中,AD∥BC,AC、BD交于O点,BA、CD的延长线交于E点,连结EO并延长分别交AD、BC于N、M
求证: BM=CM
j
A
D
B
C
E
M
N
O
1、如图,AD是∠BAC的平分线,EF是AD的垂直平分线,求证:ED2=EB·EC
F
A
B
C
E
D
2、如图,在矩形ABCD中,E是AD的中点,EF⊥EC交AB于F,连接FC(AB>AE),
求证: AEF∽ ECF
E
C
D
B
A
F
2、已知,在 ABC中,若AB=BC,∠B=90 ,AD为BC边的中线,过B作直线BP⊥AD于P交AC于E,求证:AE=2EC ;∠AEB= ∠CED.
D
A
B
C
E
二、作垂线
3. 如图从 ABCD顶点C向AB和AD的延长线引垂线CE和CF,垂足分别为E、F,求证:
证明:过B作BM⊥AC于M,过D作DN⊥AC于N
∴
∽
∴
∴
(1)
∽
∴
∴
(2)
又
∴ AN=CM
又
(1)+(2)
∴
2、中,,AC=BC,P是AB上一点,Q是PC上一点(不是中点),MN过Q且MN⊥CP,交AC、BC于M、N,求证:
2、证明:
过P作PE⊥AC于E,PF⊥CB于F,
则CEPF为矩形∴ PF
EC ∵
∴
∽
∴
∵ EC=PF ∴
(1) 在
和
中:CP⊥MN于Q ∴
又 ∵
∴
∴
∽
∴
即
由(1)(2)得
(2)
三、作延长线
例5. 如图,在梯形ABCD中,AD∥BC,若∠BCD的平分线CH⊥AB于点H,BH=3AH,且四边形AHCD的面积为21,求△HBC的面积。
分析:因为问题涉及四边形AHCD,所以可构造相似三角形。把问题转化为相似三角形的面积比而加以解决。
解:延长BA、CD交于点P
∵CH⊥AB,CD平分∠BCD
∴CB=CP,且BH=PH
∵BH=3AH
∴PA:AB=1:2
∴PA:PB=1:3
∵AD∥BC
∴△PAD∽△PBC
例6. 如图,RtABC中,CD为斜边AB上的高,E为CD的中点,AE的延长线交BC于F,FGAB于G,求证:FG=CFBF
解析:欲证式即 由“三点定形”,ΔBFG
与ΔCFG会相似吗?显然不可能。(因为ΔBFG为RtΔ),但由E为CD的中点,∴可设法构造一个与ΔBFG相似的三角形来求解。
不妨延长GF与AC的延长线交于H
则
又ED=EC ∴FG=FH 又易证RtΔCFH∽RtΔGFB
∴FG·FH=CF·BF
∵FG=FH ∴FG2=CF·BF
四、作中线
例7 如图,中,AB⊥AC,AE⊥BC于E,D在AC边上,若BD=DC=EC=1,求AC。
解:取BC的中点M,连AM
∵ AB⊥AC ∴ AM=CM
∴ ∠1=∠C 又 BD=DC
∴
∴
∽
∴
又 DC=1 MC=
BC
∴
(1)
又
∽
又 ∵ EC=1 ∴
由(1)(2)得,
∴
(2)
∴
小结:利用等腰三角形有公共底角,则这两个三角形相似,取BC中点M,构造
与
相似是解题关键
3、
理由?(用三种解法)
方法一:如图(1),设BC中点为E,连接AE。
方法二:如图(2),在DA上截取DE=DC
在△BED与△BCD中,
方法三:如图(3),过B作BE⊥BC于B,交CA的延长线于E。
我有哪些收获呢?
与大家共分享!
