鲁教版九年级上册数学第二章 解直角三角形 单元测试题(Word版无答案)
文档属性
| 名称 | 鲁教版九年级上册数学第二章 解直角三角形 单元测试题(Word版无答案) | 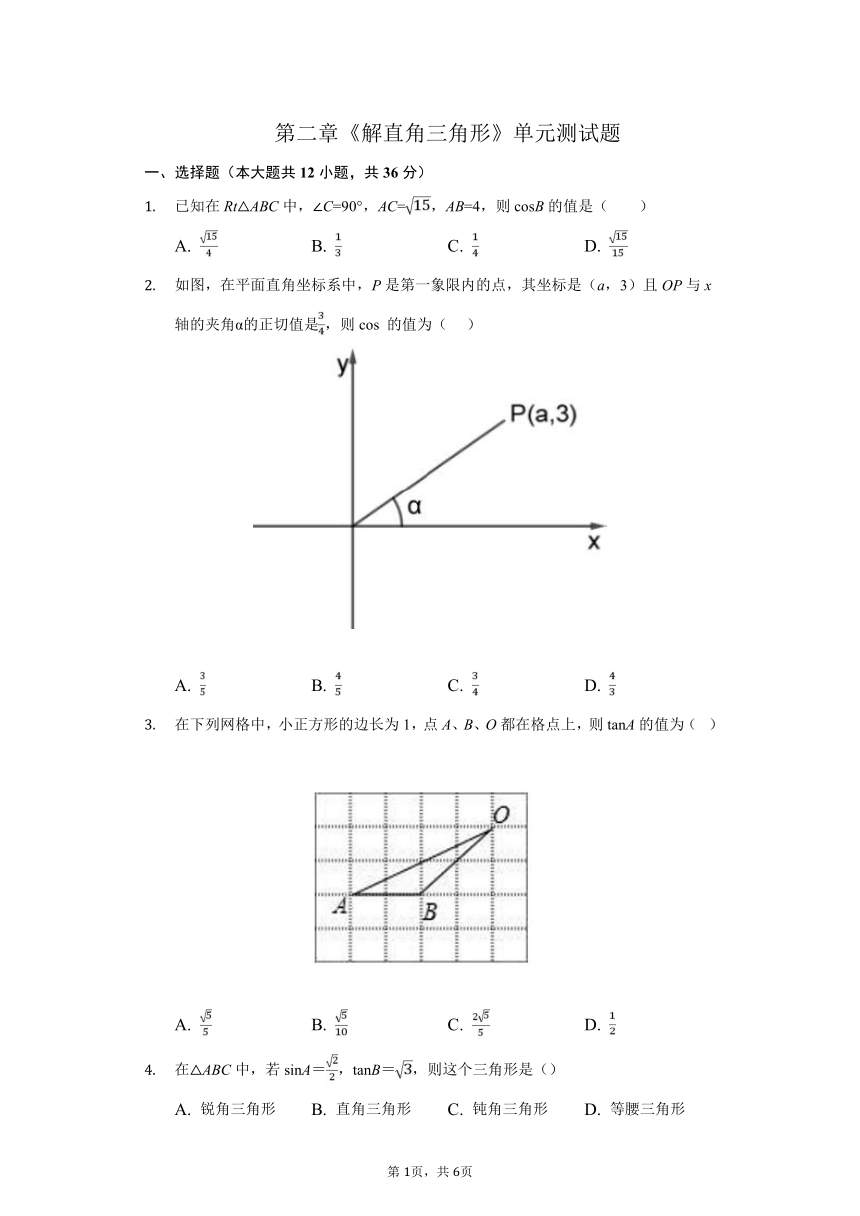 | |
| 格式 | zip | ||
| 文件大小 | 238.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 15:00:44 | ||
图片预览


文档简介
第二章《解直角三角形》单元测试题
一、选择题(本大题共12小题,共36分)
已知在Rt△ABC中,∠C=90°,AC=,AB=4,则cosB的值是( )
A.
B.
C.
D.
如图,在平面直角坐标系中,P是第一象限内的点,其坐标是(a,3)且OP与x轴的夹角α的正切值是,则cos?的值为(???
)
A.
B.
C.
D.
在下列网格中,小正方形的边长为1,点A、B、O都在格点上,则tanA的值为(?
)
A.
B.
C.
D.
在△ABC中,若sinA=,tanB=,则这个三角形是()
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
等腰三角形
在△ABC中,若|sinA-|+(1-tanB)2=0,则∠C的度数是( )
A.
45度
B.
60度
C.
75度
D.
105度
在△ABC中,AB=6,AC=6,cosB=,则BC边的长为( )
A.
9
B.
12
C.
12或6
D.
12或9
如图,四边形ABCD中∠DAB=60°,∠B=∠D=90°,BC=1,CD=2,则对角线AC的长为( )
A.
B.
C.
D.
如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是( )
A.
2
B.
4
C.
5
D.
10
如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是( )
A.
tan55°=
B.
tan55°=
C.
sin55°=
D.
cos55°=
如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AB的长度为( )
A.
6m
B.
3m
C.
9m
D.
6m
如图,一艘海轮位于灯塔P的北偏东55°方向的A处,已知PA=6海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.
6海里
B.
6cos55°海里
C.
6sin55°海里
D.
6tan55°海里
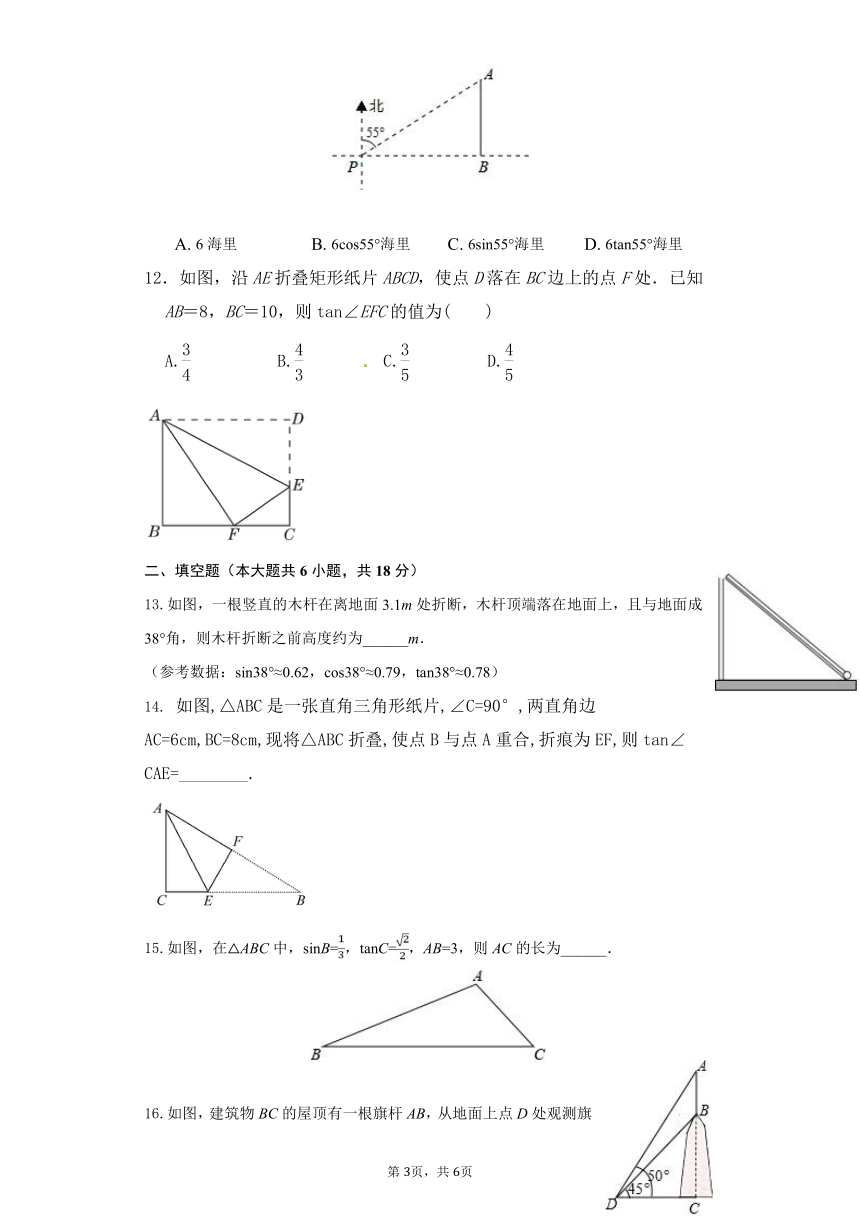
12.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边上的点F处.已知AB=8,BC=10,则tan∠EFC的值为( )
A.
B.
C.
D.
二、填空题(本大题共6小题,共18分)
13.如图,一根竖直的木杆在离地面3.1m处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为______m.
(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
14.
如图,△ABC是一张直角三角形纸片,∠C=90°,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为EF,则tan∠CAE=________.
15.如图,在△ABC中,sinB=,tanC=,AB=3,则AC的长为______.
16.如图,建筑物BC的屋顶有一根旗杆AB,从地面上点D处观测旗杆顶点A的仰角为50°,观测旗杆底部点B的仰角为45°.若旗杆的高度AB为3.5米,则建筑物BC的高度约为______米.(精确到1米,可用参考数据:sin50°≈0.8,tan50°≈1.2)
17.一艘货轮由西向东航行,在A处测得灯塔P在它的北偏东60°方向,继续航行到达B处,测得灯塔P在正南方向10海里的C处是港口,点A、B、C在一条直线上,则这艘货轮由A处到B处航行的路程为______海里(结果保留根号).
18.如图,在矩形ABCD中,AD=13,AB=24,点E是边AB上的一个动点,将CBE沿CE折叠,得到CB'E,连接AB',DB',若ADB'为等腰三角形,则BE的长为________.
三、解答题(本大题共6小题,共46分)
19.计算:
20.如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.
(1)求证:∠BEC=90°;
(2)求cos∠DAE.
21.如图,学校的教学楼对面是一幢办公楼,教学楼与办公楼的水平距离BC=30m,卓玛在教学楼顶部A处测得办公楼顶部D处的俯角α为30°,测得办公楼底部C处俯角β为60°,求办公楼的高CD.(结果保留根号)
22.2019年12月17日,国产航母山东舰正式交付中国海军,中国海军建设迈上了一个新台阶.如图,在一次训练中,笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=(12+4)海里,山东舰在点P处,从A测得山东舰在北偏西60°的方向,从B测得山东舰在北偏东45°的方向.
(1)求B、P两点之间的距离;(结果有根号的保留根号)
(2)山东舰从点P处沿射线AP的方向航行,航行30分钟后到达点C处,此时,从B测得山东舰在北偏西15°的方向.在这次训练中,山东舰的航行速度是多少?
23.如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:(1)BC的长;(2)∠ADC的正弦值.
24.如图,某教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面夹角是45°时,教学楼顶部A在地面上的影子F与墙角C的距离为18m(B、F、C在同一直线上).求教学楼AB的高;(结果保留整数)(参考数据:sim22°≈0.37,cos22°≈0.93,tan22°≈0.40)
第2页,共2页
第1页,共1页
一、选择题(本大题共12小题,共36分)
已知在Rt△ABC中,∠C=90°,AC=,AB=4,则cosB的值是( )
A.
B.
C.
D.
如图,在平面直角坐标系中,P是第一象限内的点,其坐标是(a,3)且OP与x轴的夹角α的正切值是,则cos?的值为(???
)
A.
B.
C.
D.
在下列网格中,小正方形的边长为1,点A、B、O都在格点上,则tanA的值为(?
)
A.
B.
C.
D.
在△ABC中,若sinA=,tanB=,则这个三角形是()
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
等腰三角形
在△ABC中,若|sinA-|+(1-tanB)2=0,则∠C的度数是( )
A.
45度
B.
60度
C.
75度
D.
105度
在△ABC中,AB=6,AC=6,cosB=,则BC边的长为( )
A.
9
B.
12
C.
12或6
D.
12或9
如图,四边形ABCD中∠DAB=60°,∠B=∠D=90°,BC=1,CD=2,则对角线AC的长为( )
A.
B.
C.
D.
如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是( )
A.
2
B.
4
C.
5
D.
10
如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是( )
A.
tan55°=
B.
tan55°=
C.
sin55°=
D.
cos55°=
如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AB的长度为( )
A.
6m
B.
3m
C.
9m
D.
6m
如图,一艘海轮位于灯塔P的北偏东55°方向的A处,已知PA=6海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.
6海里
B.
6cos55°海里
C.
6sin55°海里
D.
6tan55°海里
12.如图,沿AE折叠矩形纸片ABCD,使点D落在BC边上的点F处.已知AB=8,BC=10,则tan∠EFC的值为( )
A.
B.
C.
D.
二、填空题(本大题共6小题,共18分)
13.如图,一根竖直的木杆在离地面3.1m处折断,木杆顶端落在地面上,且与地面成38°角,则木杆折断之前高度约为______m.
(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
14.
如图,△ABC是一张直角三角形纸片,∠C=90°,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为EF,则tan∠CAE=________.
15.如图,在△ABC中,sinB=,tanC=,AB=3,则AC的长为______.
16.如图,建筑物BC的屋顶有一根旗杆AB,从地面上点D处观测旗杆顶点A的仰角为50°,观测旗杆底部点B的仰角为45°.若旗杆的高度AB为3.5米,则建筑物BC的高度约为______米.(精确到1米,可用参考数据:sin50°≈0.8,tan50°≈1.2)
17.一艘货轮由西向东航行,在A处测得灯塔P在它的北偏东60°方向,继续航行到达B处,测得灯塔P在正南方向10海里的C处是港口,点A、B、C在一条直线上,则这艘货轮由A处到B处航行的路程为______海里(结果保留根号).
18.如图,在矩形ABCD中,AD=13,AB=24,点E是边AB上的一个动点,将CBE沿CE折叠,得到CB'E,连接AB',DB',若ADB'为等腰三角形,则BE的长为________.
三、解答题(本大题共6小题,共46分)
19.计算:
20.如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.
(1)求证:∠BEC=90°;
(2)求cos∠DAE.
21.如图,学校的教学楼对面是一幢办公楼,教学楼与办公楼的水平距离BC=30m,卓玛在教学楼顶部A处测得办公楼顶部D处的俯角α为30°,测得办公楼底部C处俯角β为60°,求办公楼的高CD.(结果保留根号)
22.2019年12月17日,国产航母山东舰正式交付中国海军,中国海军建设迈上了一个新台阶.如图,在一次训练中,笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=(12+4)海里,山东舰在点P处,从A测得山东舰在北偏西60°的方向,从B测得山东舰在北偏东45°的方向.
(1)求B、P两点之间的距离;(结果有根号的保留根号)
(2)山东舰从点P处沿射线AP的方向航行,航行30分钟后到达点C处,此时,从B测得山东舰在北偏西15°的方向.在这次训练中,山东舰的航行速度是多少?
23.如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:(1)BC的长;(2)∠ADC的正弦值.
24.如图,某教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面夹角是45°时,教学楼顶部A在地面上的影子F与墙角C的距离为18m(B、F、C在同一直线上).求教学楼AB的高;(结果保留整数)(参考数据:sim22°≈0.37,cos22°≈0.93,tan22°≈0.40)
第2页,共2页
第1页,共1页
