鲁教版九年级上册数学第二章直角三角形的边角关系 复习课课件(29张)
文档属性
| 名称 | 鲁教版九年级上册数学第二章直角三角形的边角关系 复习课课件(29张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 18:18:32 | ||
图片预览






文档简介
(共29张PPT)
解直角三角形复习课
义务教育教科书
九年级上册
数
学
三角函数的定义
解直角三角形
解直角三角形
解直角三角形
的应用
知识树
(一)锐角三角函数(三角比)
1、定义:sinA=
cosA=
tanA=
2、性质
1、∠A是锐角,请说一说sinA和cosA的取值范围.
00tanA的取值范围是多少?
tanA>0
3、请说一说互为余角的三角函数之间的关系
sin(900-A)=cosA
cos(900
–A)=sinA
4、同角的三角函数关系
(1)、平方关系:
sin2A+cos2A=1
(2)、商数关系:
tanA=
跟踪练习(一)
1.如图,sinA的值等(
).
(A)
(B)2
(C)
(D)
2
1
C
跟踪练习(一)
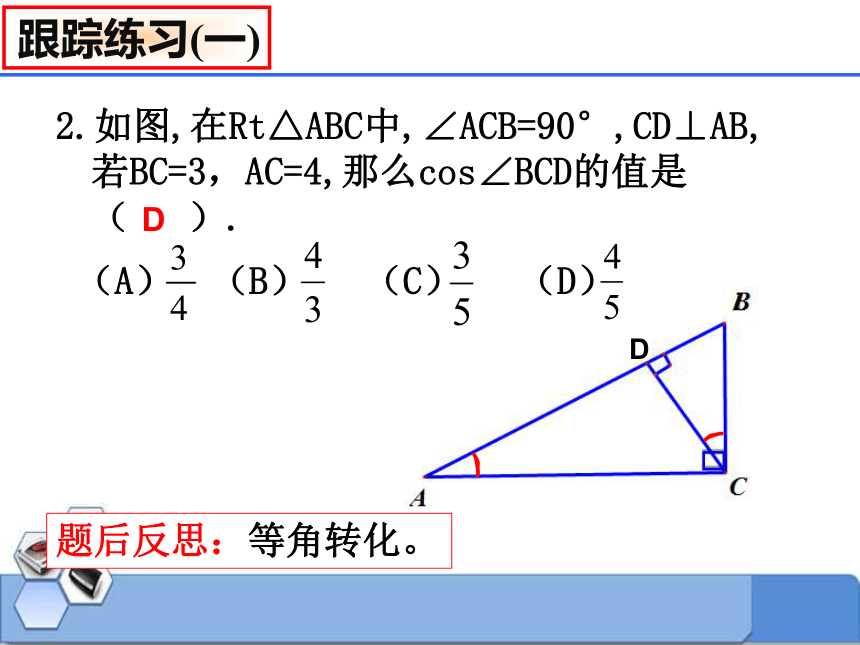
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,若BC=3,AC=4,那么cos∠BCD的值是(
).
D
(A)
(B)
(C)
(D)
D
题后反思:等角转化。
跟踪练习(一)
3.如图,在网格中,小正方形的边长均为1,点A、B、C都在格点上,则∠ABC的正切值是
_____.
题后反思:求一个角的三角函数值,必须把这个角放在Rt△中研究。
跟踪练习(一)
4、在Rt△ABC中,∠C=90°,若将各边长度都扩大为原来的2倍,则∠A的正弦值( )
A.扩大2倍
B.缩小2倍
C.扩大4倍
D.不变
D
【解析】在直角三角形中,∠A的正弦是∠A的对边与斜边的比值,当∠A固定时,其正弦值也是一个固定值,所以当直角三角形各边都扩大2倍时,其比值不变,故选择D.
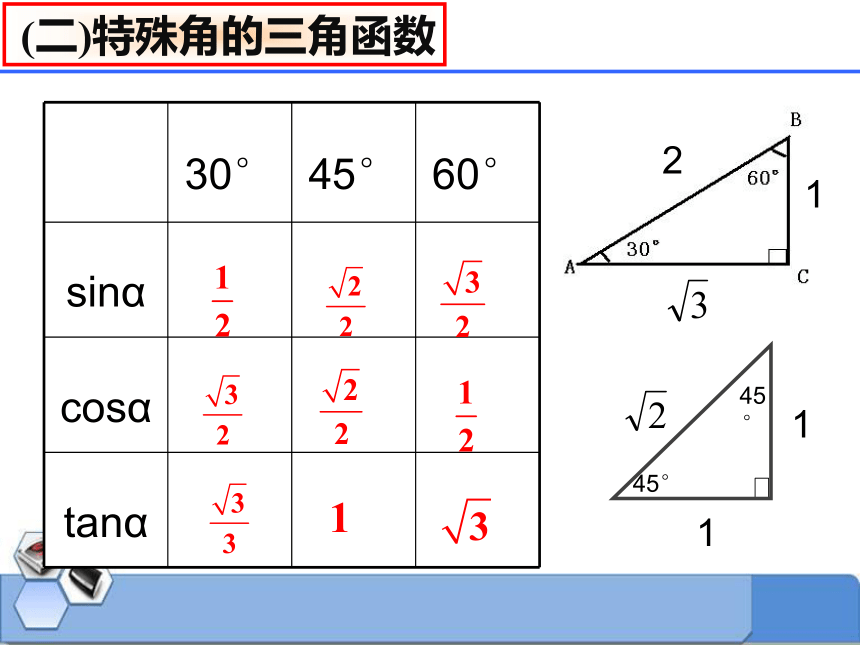
30°
45°
60°
sinα
cosα
tanα
45°
45°
1
1
1
2
(二)特殊角的三角函数
1.在Rt△ABC中,cosB=
,
则tanA=
.
2、计算:sin30°·cos30°-tan30°=________(结果保留根号).
跟踪练习(二)
C
(三)解直角三角形
在Rt△ABC中,∠C为直角,除直角C外,其余的元素有哪些?它们之间有什么关系?
A
B
C
c
b
a
利用这些关系,如果知道直角三角形的哪几个元素就可以求其他的元素了
在Rt△ABC中,∠C为直角,∠A、∠B为锐角,它们所对的边分别为c
、a、b,其中除直角C外,其余的5个元素之间有以下关系:
A
B
C
c
b
a
sinA=
c
a
cosA=
c
b
tanA=
b
a
∠A
+
∠B
=
90
°;
a2+b2=c2
;
(3)角与边之间的关系:
(2)边之间的关系:
(1)角之间的关系:
,
,
两个元素(至少一个是边)
两个角
两条边
一边一角
×
√
√
.解直角三角形的定义
由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.(直角三角形中,除直角外,一共有5个元素即3条边和2个锐角)
解直角三角形的几种基本类型
直角边a
斜边c
B=900-A;b=a/tanA
C=a/sinA
直角边a
锐角A
两直角边
a、b
斜边c,
锐角A
两边
B=900-A;a=csinA
b=c
cosA
一边一锐角
一般解法
已知条件
A
C
B
a
b
c
例1、如图,在△ABC中,已知∠A﹦60°,∠B﹦45°,AC﹦12,求AB的长。
A
C
B
D
?ABC不是直角三角形怎么办?
转化思想:作AB边上的高,把锐角三角形转化为直角三角形,把问题转化为解直角三角形!
化未知为已知!
例题讲解
A
C
B
D
解:过点C作CD⊥AB,垂足为点D。
例1.如图,在△ABC中,已知∠A﹦60°,∠B﹦45°,AC﹦12,求AB的长。
解直角三角形复习课
义务教育教科书
九年级上册
数
学
三角函数的定义
解直角三角形
解直角三角形
解直角三角形
的应用
知识树
(一)锐角三角函数(三角比)
1、定义:sinA=
cosA=
tanA=
2、性质
1、∠A是锐角,请说一说sinA和cosA的取值范围.
0
tanA>0
3、请说一说互为余角的三角函数之间的关系
sin(900-A)=cosA
cos(900
–A)=sinA
4、同角的三角函数关系
(1)、平方关系:
sin2A+cos2A=1
(2)、商数关系:
tanA=
跟踪练习(一)
1.如图,sinA的值等(
).
(A)
(B)2
(C)
(D)
2
1
C
跟踪练习(一)
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,若BC=3,AC=4,那么cos∠BCD的值是(
).
D
(A)
(B)
(C)
(D)
D
题后反思:等角转化。
跟踪练习(一)
3.如图,在网格中,小正方形的边长均为1,点A、B、C都在格点上,则∠ABC的正切值是
_____.
题后反思:求一个角的三角函数值,必须把这个角放在Rt△中研究。
跟踪练习(一)
4、在Rt△ABC中,∠C=90°,若将各边长度都扩大为原来的2倍,则∠A的正弦值( )
A.扩大2倍
B.缩小2倍
C.扩大4倍
D.不变
D
【解析】在直角三角形中,∠A的正弦是∠A的对边与斜边的比值,当∠A固定时,其正弦值也是一个固定值,所以当直角三角形各边都扩大2倍时,其比值不变,故选择D.
30°
45°
60°
sinα
cosα
tanα
45°
45°
1
1
1
2
(二)特殊角的三角函数
1.在Rt△ABC中,cosB=
,
则tanA=
.
2、计算:sin30°·cos30°-tan30°=________(结果保留根号).
跟踪练习(二)
C
(三)解直角三角形
在Rt△ABC中,∠C为直角,除直角C外,其余的元素有哪些?它们之间有什么关系?
A
B
C
c
b
a
利用这些关系,如果知道直角三角形的哪几个元素就可以求其他的元素了
在Rt△ABC中,∠C为直角,∠A、∠B为锐角,它们所对的边分别为c
、a、b,其中除直角C外,其余的5个元素之间有以下关系:
A
B
C
c
b
a
sinA=
c
a
cosA=
c
b
tanA=
b
a
∠A
+
∠B
=
90
°;
a2+b2=c2
;
(3)角与边之间的关系:
(2)边之间的关系:
(1)角之间的关系:
,
,
两个元素(至少一个是边)
两个角
两条边
一边一角
×
√
√
.解直角三角形的定义
由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.(直角三角形中,除直角外,一共有5个元素即3条边和2个锐角)
解直角三角形的几种基本类型
直角边a
斜边c
B=900-A;b=a/tanA
C=a/sinA
直角边a
锐角A
两直角边
a、b
斜边c,
锐角A
两边
B=900-A;a=csinA
b=c
cosA
一边一锐角
一般解法
已知条件
A
C
B
a
b
c
例1、如图,在△ABC中,已知∠A﹦60°,∠B﹦45°,AC﹦12,求AB的长。
A
C
B
D
?ABC不是直角三角形怎么办?
转化思想:作AB边上的高,把锐角三角形转化为直角三角形,把问题转化为解直角三角形!
化未知为已知!
例题讲解
A
C
B
D
解:过点C作CD⊥AB,垂足为点D。
例1.如图,在△ABC中,已知∠A﹦60°,∠B﹦45°,AC﹦12,求AB的长。
