四川省成都新津为明学校2020-2021学年八年级上学期期中测试数学试卷(Word版 含答案)
文档属性
| 名称 | 四川省成都新津为明学校2020-2021学年八年级上学期期中测试数学试卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 293.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 17:27:48 | ||
图片预览



文档简介
2020~2021学年度上期
期中考试
初二(初2022届)
数学试题
(说明:本卷满分150分,其中A卷100分,B卷50分,考试时间120分钟)
学校:_____
____姓名:____
_
____班级:___
_
_____考号:___
___
___
注意事项:1、答题前填写好自己的姓名、班级、考号等信息
2、请将答案正确填写在答题卡上
A卷(100分)
一、选择题(每题3分,共30分)
1.(3分)下列实数中,属于有理数的是( )
A.
B.
C.π
D.
2.
下列函数中y是x的一次函数的是(
)
A.
B.
C.
D.
3.(3分)若,则x+y等于( )
A.﹣1
B.1
C.3
D.﹣3
4.(3分)下列四组数据不能作为直角三角形的三边长的是( )
A.6、8、10
B.5、12、13
C.7、10、12
D.3、4、5
点(﹣2,6)在正比例函数y=kx图象上,请问k的值是( )
A.
3
B.
﹣3
C.
1
D.
﹣1
6.(3分)若点A(﹣1,3)在第(
)象限
A.一
B.二
C.三
D.四
7.(3分)已知小明从A地到B地,速度为4千米/小时,A、B两地相距3千米,若用x(小时)表示行走的时间,y(千米)表示余下的路程,则y与x之间的函数表达式是( )
A.y=4x
B.y=4x﹣3
C.y=﹣4x
D.y=﹣4x+3
8.(3分)若一次函数y=kx﹣1的函数值y随着x的增大而减小,则( )
A.k>1
B.k<1
C.k>0
D.k<0
9.(3分)若直角三角形两直角边长分别为5,12,则斜边上的高为( )
A.6
B.8
C.
D.
10.(3分)对于一次函数y=3x+2,①图象必经过点(﹣1,﹣1);②图象经过第一、二、四象限;③当x>1时,y<0;④y的值随着x值的增大而增大,以上结论正确的个数是( )
A.0个
B.1个
C.2个
D.3个
二、填空题
11.(4分)8的立方根是
.
12.(4分)如图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF=
.
13.(4分)一次函数的图象不经过第________象限
14.(4分)若函数y=2x+(1﹣m)是正比例函数,则m的值是
.
三、解答题
15.(10分)计算
(1)化简:
(2)化简:
16.(10分)解方程
(1)4x2﹣16=0
(2)
17.(8分)先化简,再求值:(2a﹣3)(a+1)﹣a(a﹣3),其中a1.
18.(8分)△ABC在直角坐标系内的位置如图.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标.
更正通知:
(8分)修改为:已知,,求2x2﹣xy+2y2的值.
20.(10分)在平面直角坐标系中,点A(2,2),点B(0,-
4),直线AB交x轴于点C.试求
(1)直线AB的表达式;
(2)点C的坐标;
(3)在平面直角坐标系中画出直线AB;
(4)求三角形AOB的面积。
B卷(共50分)
一、填空题(每题4分,共20分)
21.(4分)已知2a﹣1的平方根是±3,3a﹣b﹣1的立方根是2,a+b的平方根
.
22.(4分)已知点A(m﹣5,1),点B(4,m+1),且直线AB∥y轴,则m=
.
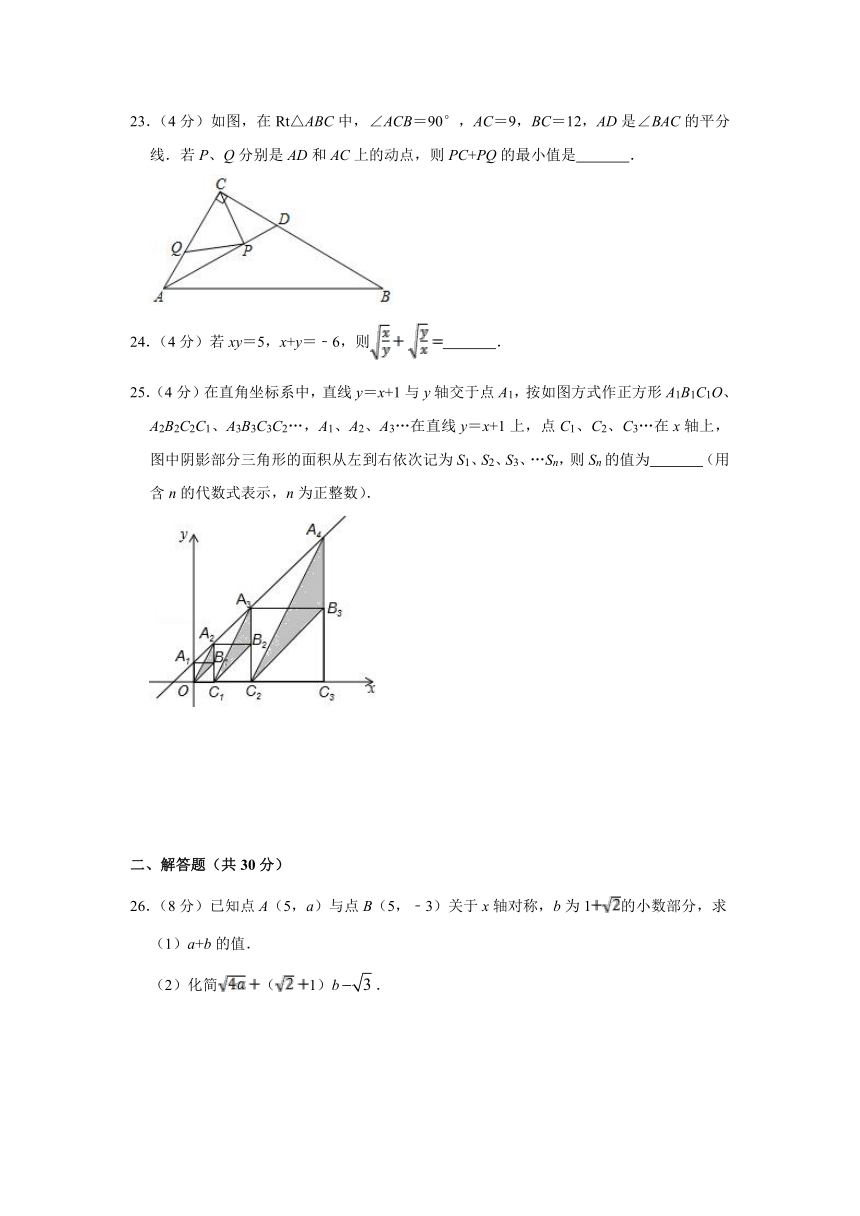
23.(4分)如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AD是∠BAC的平分线.若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是
.
24.(4分)若xy=5,x+y=﹣6,则
.
25.(4分)在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn,则Sn的值为
(用含n的代数式表示,n为正整数).
二、解答题(共30分)
26.(8分)已知点A(5,a)与点B(5,﹣3)关于x轴对称,b为1的小数部分,求
(1)a+b的值.
(2)化简(1)b.
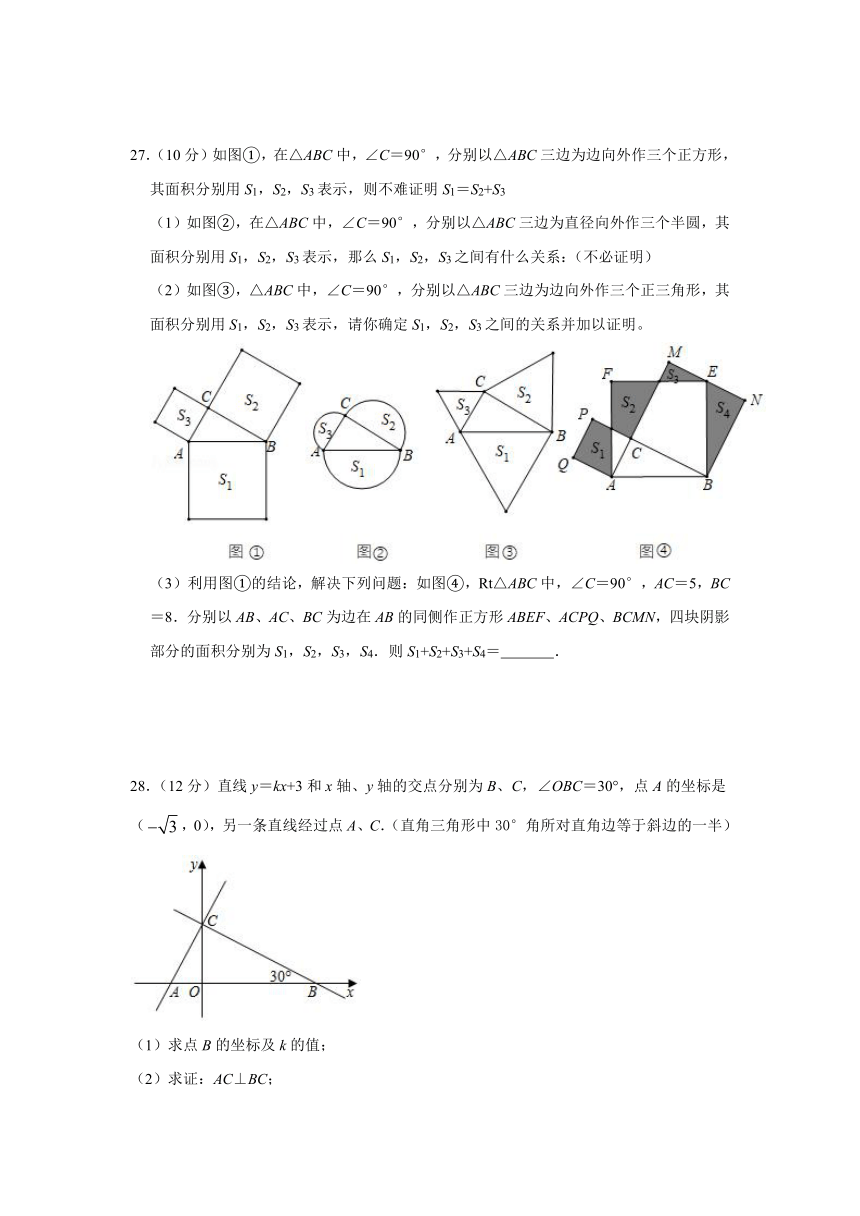
27.(10分)如图①,在△ABC中,∠C=90°,分别以△ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3
(1)如图②,在△ABC中,∠C=90°,分别以△ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系:(不必证明)
(2)如图③,△ABC中,∠C=90°,分别以△ABC三边为边向外作三个正三角形,其面积分别用S1,S2,S3表示,请你确定S1,S2,S3之间的关系并加以证明。
利用图①的结论,解决下列问题:如图④,Rt△ABC中,∠C=90°,AC=5,BC=8.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1,S2,S3,S4.则S1+S2+S3+S4=
.
28.(12分)直线y=kx+3和x轴、y轴的交点分别为B、C,∠OBC=30°,点A的坐标是(,0),另一条直线经过点A、C.(直角三角形中30°角所对直角边等于斜边的一半)
(1)求点B的坐标及k的值;
(2)求证:AC⊥BC;
(3)点M为直线BC上一点(与点B不重合),设点M的横坐标为x,△ABM的面积为S.
①求S与x的函数关系式;
②当S=6时,求点M的坐标.
初二数学期中试卷A卷
参考答案与试题解析
一、选择题
1.(3分)下列实数中,属于有理数的是( )
A.
B.
C.
D.
【解答】解:A、二次根下8不能正好开方,即为无理数,故本选项错误,
B、分数为有理数,符合;
C、π为无理数,所以为无理数,故本选项错误;
D、不能正好开方,为无理数,故本选项错误.
故选:B.
【点评】本题考查实数范围内的有理数的判断,从实际出发有理数有分数,自然数等,无理数有π、根式下开不尽的从而得到了答案.
2.(3分)下列函数中y是x的一次函数的是(
)
A.
B.
C.
D.
【解答】B
【点评】此题主要考查了关于x轴对称点的坐标,关键是掌握点的坐标的变化规律.
3.A.
【点评】本题考查了非负数的性质.解题的关键是掌握非负数的性质:几个非负数的和为0时,这几个非负数都为0.
4.(3分)下列四组数据不能作为直角三角形的三边长的是( )
A.6、8、10
B.5、12、13
C.7、10、12
D.3、4、5
【解答】解:A、62+82=102,能组成直角三角形,故此选项不合题意;
B、52+122=132,能组成直角三角形,故此选项不合题意;
C、72+102≠122,不能组成直角三角形,故此选项符合题意;
D、32+42=52,能组成直角三角形,故此选项错不合题意;
故选:C.
【点评】此题主要考查了勾股定理逆定理,关键是掌握判断一个三角形是不是直角三角形.必须满足较小两边平方的和等于最大边的平方才能做出判断.
5.【解答】B.
6.B
【点评】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点.用到的知识点为:第二象限点的符号为(﹣,+).
7.(3分)已知小明从A地到B地,速度为4千米/小时,A、B两地相距3千米,若用x(小时)表示行走的时间,y(千米)表示余下的路程,则y与x之间的函数表达式是( )
A.y=4x
B.y=4x﹣3
C.y=﹣4x
D.y=﹣4x+3
【解答】解:用x(小时)表示行走的时间,y(千米)表示余下的路程,
则y与x之间的函数表达式是:y=3﹣4x=﹣4x+3.
故选:D.
【点评】此题主要考查了根据实际问题列一次函数解析式,正确理解题意表示出行驶路程是解题的关键.
8.D
【点评】本题考查了一次函数的性质,在一次函数y=kx+b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
9.(3分)若直角三角形两直角边长分别为5,12,则斜边上的高为( )
A.6
B.8
C.
D.
【解答】解:根据勾股定理可得:斜边长2=52+122,
则斜边长=13,
直角三角形面积S5×1213×斜边的高,
解得:斜边的高;
故选:D.
10.(3分)对于一次函数y=3x+2,①图象必经过点(﹣1,﹣1);②图象经过第一、二、四象限;③当x>1时,y<0;④y的值随着x值的增大而增大,以上结论正确的个数是( )
A.0个
B.1个
C.2个
D.3个
【解答】解:①当x=﹣1时,y=﹣3+2=﹣1,故正确;
②k=3>0,b=2>0,故图象经过第一、二、三象限,故错误;
③y=0时,x,故x时,y<0,故错误;
④k=3>0,故y的值随着x值的增大而增大,正确;
故选:C.
【点评】本题考查的是一次函数图象上点的坐标特征,由k值的符号,确定函数的增减性即可求解.
二、填空题
11.(4分)8的立方根是 2 .
【解答】解:8的立方根为2,
故答案为:2.
【点评】此题考查了立方根,熟练掌握立方根的定义是解本题的关键.
12.(4分)6
=13.(4分)一次函数的图象不经过第________象限
【解答】故答案为:三.
【点评】本题考查了点的坐标,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
14.(4分)若函数y=2x+(1﹣m)是正比例函数,则m的值是 1 .
【解答】解:∵函数y=2x+(1﹣m)是正比例函数,
∴1﹣m=0,
解得:m=1.
故答案为:1.
【点评】此题主要考查了正比例函数的定义,正确掌握正比例函数的定义是解题关键.
三、解答题
15.(20分)计算
(1)化简:
(2)化简:
16.(1)解方程:
(2)解方程:
17.(8分)先化简,再求值:(2a﹣3)(a+1)﹣a(a﹣3),其中a1.
【解答】解:(2a﹣3)(a+1)﹣a(a﹣3)
=2a2﹣a﹣3﹣a2+3a
=a2+2a﹣3,
当a1时,原式=(1)2+2(1)﹣3=2﹣21+22﹣3=﹣2.
【点评】本题考查整式的混合运算﹣化简求值,解答本题的关键是明确整式化简求值的方法.
18.(8分)△ABC在直角坐标系内的位置如图.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标.
【解答】解:(1)A(0,3),B(﹣4,4),C(﹣2,1);
(2)△A1B1C1如图所示,B1(4,4).
【点评】本题考查了利用轴对称作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.
19.
【解答】解:
2x2﹣xy+2y2
=2(x﹣y)2+3xy
=2×()2+3
=2×1+3
=2
.
(10分)略
八上数学期中B卷
参考答案与试题解析
一、填空题
21.(4分)已知2a﹣1的平方根是±3,3a﹣b﹣1的立方根是2,a+b的平方根 ± .
【解答】解:由题意,有,
解得.
则a+b=5+6=11,
所以a+b的平方根±.
故答案为:±.
【点评】本题考查了平方根、立方根的定义.解题的关键是掌握平方根、立方根的定义.如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.如果一个数x的立方等于a,那么这个数x就叫做a的立方根.
22.(4分)已知点A(m﹣5,1),点B(4,m+1),且直线AB∥y轴,则m= 9 .
【解答】解:∵点A(m﹣5,1),点B(4,m+1),且直线AB∥y轴,
∴m﹣5=4,
解得m=9.
故答案是:9.
【点评】本题考查了坐标与图形性质.需要掌握平行于坐标轴直线上点的坐标特征.
23.(4分)如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AD是∠BAC的平分线.若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是 .
【解答】解:过点D作DE⊥AB于点E,过点E作EQ⊥AC于点Q,EQ交AD于点P,连接CP,此时PC+PQ=EQ取最小值,如图所示.
在Rt△ABC中,∠ACB=90°,AC=9,BC=12,
∴AB═15.
∵AD是∠BAC的平分线,
∴∠CAD=∠EAD,
在△ACD和△AED中,
∴△ACD≌△AED(AAS),
∴AE=AC=9.
∵EQ⊥AC,∠ACB=90°,
∴EQ∥BC,
∴,
即,
∴EQ,
故答案为.
【点评】本题考查了勾股定理、轴对称中的最短路线问题以及平行线的性质,找出点P、Q的位置是解题的关键.
4.(4分)若xy=5,x+y=﹣6,则 .
【解答】解:∵xy=5,x+y=﹣6,
∴x<0,y<0,
∴(),
故答案为:.
【点评】本题考查的是二次根式的化简求值,掌握二次根式的混合运算法则是解题的关键.
5.(4分)在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn,则Sn的值为 22n﹣3 (用含n的代数式表示,n为正整数).
【解答】方法一:
解:∵直线y=x+1,当x=0时,y=1,当y=0时,x=﹣1,
∴OA1=1,OD=1,
∴∠ODA1=45°,
∴∠A2A1B1=45°,
∴A2B1=A1B1=1,
∴S11×1,
∵A2B1=A1B1=1,
∴A2C1=2=21,
∴S2(21)2=21
同理得:A3C2=4=22,…,
S3(22)2=23
∴Sn(2n﹣1)2=22n﹣3
故答案为:22n﹣3.
方法二:
∵y=x+1,正方形A1B1C1O,
∴OA1=OC1=1,A2C1=2,B1C1=1,
∴A2B1=1,S1,
∵OC2=1+2=3,
∴A3C2=4,B2C2=2,
∴A3B2=2,
S2=2,
∴q4,
∴Sn.
【点评】本题考查了一次函数图象上点的坐标特征以及正方形的性质;通过求出第一个正方形、第二个正方形和第三个正方形的边长得出规律是解决问题的关键.
二、解答题
26.(8分)已知点A(5,a)与点B(5,﹣3)关于x轴对称,b为1的小数部分,求
(1)a+b的值.
(2)化简(1)b.
【解答】解:(1∵点A(5,a)与点B(5,﹣3)关于x轴对称,
∴a=3.
∵12,
∴b1.
∴以a+b1+32.
(2)将a、b的值代入得:原式(1)(1)=22﹣1=+1.
【点评】本题主要考查的是二次根式的混合运算,熟练掌握运算法则是解题的关键.
27.(10分)如图①,在△ABC中,∠C=90°,分别以△ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3
(1)如图②,在△ABC中,∠C=90°,分别以△ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系:(不必证明)
(2)如图③,△ABC中,∠C=90°,分别以△ABC三边为边向外作三个正三角形,其面积分别用S1,S2,S3表示,请你确定S1,S2,S3之间的关系并加以证明
(3)利用图①的结论,解决下列问题:如图④,Rt△ABC中,∠C=90°,AC=5,BC=8.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1,S2,S3,S4.则S1+S2+S3+S4= 60 .
【解答】解:(1)如图(2),分别以Rt△ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,那么S1=S2+S3,
理由为:在Rt△ABC中,利用勾股定理得:AB2=AC2+BC2,
∴AB2AC2BC2,即S1=S2+S3;
(2)如图(3),分别以Rt△ABC三边为边向外作三个正三角形,其面积分别用
S1、S2、S3表示,S1、S2、S3之间的关系为S1=S2+S3,
理由为:在Rt△ABC中,利用勾股定理得:AB2=AC2+BC2,
∴AB2AC2BC2,即S1=S2+S3;
(3)过F作AM的垂线交AM于D,
∴DF∥PC,
可证明Rt△ADF≌Rt△ABC,Rt△DFK≌Rt△CAT,
所以FD=AC=CP,
∴四边形CDFP是矩形,
∴∠CPF=90°,
∵∠QPC=90°,
∴∠QPF=180°,
∴Q,P,F三点共线,S2=SRt△ABC.
由Rt△DFK≌Rt△CAT可进一步证得:Rt△FPT≌Rt△EMK,
∴S3=S△FPT,
又可证得Rt△AQF≌Rt△ACB,
∴S1+S3=SRt△AQF=SRt△ABC.
易证Rt△ABC≌Rt△EBN,
∴S4=SRt△ABC,
∴S1+S2+S3+S4
=(S1+S3)+S2+S4
=SRt△ABC+SRt△ABC+SRt△ABC
=SRt△ABC×3
=5×8÷2×3
=60.
期中考试
初二(初2022届)
数学试题
(说明:本卷满分150分,其中A卷100分,B卷50分,考试时间120分钟)
学校:_____
____姓名:____
_
____班级:___
_
_____考号:___
___
___
注意事项:1、答题前填写好自己的姓名、班级、考号等信息
2、请将答案正确填写在答题卡上
A卷(100分)
一、选择题(每题3分,共30分)
1.(3分)下列实数中,属于有理数的是( )
A.
B.
C.π
D.
2.
下列函数中y是x的一次函数的是(
)
A.
B.
C.
D.
3.(3分)若,则x+y等于( )
A.﹣1
B.1
C.3
D.﹣3
4.(3分)下列四组数据不能作为直角三角形的三边长的是( )
A.6、8、10
B.5、12、13
C.7、10、12
D.3、4、5
点(﹣2,6)在正比例函数y=kx图象上,请问k的值是( )
A.
3
B.
﹣3
C.
1
D.
﹣1
6.(3分)若点A(﹣1,3)在第(
)象限
A.一
B.二
C.三
D.四
7.(3分)已知小明从A地到B地,速度为4千米/小时,A、B两地相距3千米,若用x(小时)表示行走的时间,y(千米)表示余下的路程,则y与x之间的函数表达式是( )
A.y=4x
B.y=4x﹣3
C.y=﹣4x
D.y=﹣4x+3
8.(3分)若一次函数y=kx﹣1的函数值y随着x的增大而减小,则( )
A.k>1
B.k<1
C.k>0
D.k<0
9.(3分)若直角三角形两直角边长分别为5,12,则斜边上的高为( )
A.6
B.8
C.
D.
10.(3分)对于一次函数y=3x+2,①图象必经过点(﹣1,﹣1);②图象经过第一、二、四象限;③当x>1时,y<0;④y的值随着x值的增大而增大,以上结论正确的个数是( )
A.0个
B.1个
C.2个
D.3个
二、填空题
11.(4分)8的立方根是
.
12.(4分)如图将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF=
.
13.(4分)一次函数的图象不经过第________象限
14.(4分)若函数y=2x+(1﹣m)是正比例函数,则m的值是
.
三、解答题
15.(10分)计算
(1)化简:
(2)化简:
16.(10分)解方程
(1)4x2﹣16=0
(2)
17.(8分)先化简,再求值:(2a﹣3)(a+1)﹣a(a﹣3),其中a1.
18.(8分)△ABC在直角坐标系内的位置如图.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标.
更正通知:
(8分)修改为:已知,,求2x2﹣xy+2y2的值.
20.(10分)在平面直角坐标系中,点A(2,2),点B(0,-
4),直线AB交x轴于点C.试求
(1)直线AB的表达式;
(2)点C的坐标;
(3)在平面直角坐标系中画出直线AB;
(4)求三角形AOB的面积。
B卷(共50分)
一、填空题(每题4分,共20分)
21.(4分)已知2a﹣1的平方根是±3,3a﹣b﹣1的立方根是2,a+b的平方根
.
22.(4分)已知点A(m﹣5,1),点B(4,m+1),且直线AB∥y轴,则m=
.
23.(4分)如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AD是∠BAC的平分线.若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是
.
24.(4分)若xy=5,x+y=﹣6,则
.
25.(4分)在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn,则Sn的值为
(用含n的代数式表示,n为正整数).
二、解答题(共30分)
26.(8分)已知点A(5,a)与点B(5,﹣3)关于x轴对称,b为1的小数部分,求
(1)a+b的值.
(2)化简(1)b.
27.(10分)如图①,在△ABC中,∠C=90°,分别以△ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3
(1)如图②,在△ABC中,∠C=90°,分别以△ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系:(不必证明)
(2)如图③,△ABC中,∠C=90°,分别以△ABC三边为边向外作三个正三角形,其面积分别用S1,S2,S3表示,请你确定S1,S2,S3之间的关系并加以证明。
利用图①的结论,解决下列问题:如图④,Rt△ABC中,∠C=90°,AC=5,BC=8.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1,S2,S3,S4.则S1+S2+S3+S4=
.
28.(12分)直线y=kx+3和x轴、y轴的交点分别为B、C,∠OBC=30°,点A的坐标是(,0),另一条直线经过点A、C.(直角三角形中30°角所对直角边等于斜边的一半)
(1)求点B的坐标及k的值;
(2)求证:AC⊥BC;
(3)点M为直线BC上一点(与点B不重合),设点M的横坐标为x,△ABM的面积为S.
①求S与x的函数关系式;
②当S=6时,求点M的坐标.
初二数学期中试卷A卷
参考答案与试题解析
一、选择题
1.(3分)下列实数中,属于有理数的是( )
A.
B.
C.
D.
【解答】解:A、二次根下8不能正好开方,即为无理数,故本选项错误,
B、分数为有理数,符合;
C、π为无理数,所以为无理数,故本选项错误;
D、不能正好开方,为无理数,故本选项错误.
故选:B.
【点评】本题考查实数范围内的有理数的判断,从实际出发有理数有分数,自然数等,无理数有π、根式下开不尽的从而得到了答案.
2.(3分)下列函数中y是x的一次函数的是(
)
A.
B.
C.
D.
【解答】B
【点评】此题主要考查了关于x轴对称点的坐标,关键是掌握点的坐标的变化规律.
3.A.
【点评】本题考查了非负数的性质.解题的关键是掌握非负数的性质:几个非负数的和为0时,这几个非负数都为0.
4.(3分)下列四组数据不能作为直角三角形的三边长的是( )
A.6、8、10
B.5、12、13
C.7、10、12
D.3、4、5
【解答】解:A、62+82=102,能组成直角三角形,故此选项不合题意;
B、52+122=132,能组成直角三角形,故此选项不合题意;
C、72+102≠122,不能组成直角三角形,故此选项符合题意;
D、32+42=52,能组成直角三角形,故此选项错不合题意;
故选:C.
【点评】此题主要考查了勾股定理逆定理,关键是掌握判断一个三角形是不是直角三角形.必须满足较小两边平方的和等于最大边的平方才能做出判断.
5.【解答】B.
6.B
【点评】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点.用到的知识点为:第二象限点的符号为(﹣,+).
7.(3分)已知小明从A地到B地,速度为4千米/小时,A、B两地相距3千米,若用x(小时)表示行走的时间,y(千米)表示余下的路程,则y与x之间的函数表达式是( )
A.y=4x
B.y=4x﹣3
C.y=﹣4x
D.y=﹣4x+3
【解答】解:用x(小时)表示行走的时间,y(千米)表示余下的路程,
则y与x之间的函数表达式是:y=3﹣4x=﹣4x+3.
故选:D.
【点评】此题主要考查了根据实际问题列一次函数解析式,正确理解题意表示出行驶路程是解题的关键.
8.D
【点评】本题考查了一次函数的性质,在一次函数y=kx+b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
9.(3分)若直角三角形两直角边长分别为5,12,则斜边上的高为( )
A.6
B.8
C.
D.
【解答】解:根据勾股定理可得:斜边长2=52+122,
则斜边长=13,
直角三角形面积S5×1213×斜边的高,
解得:斜边的高;
故选:D.
10.(3分)对于一次函数y=3x+2,①图象必经过点(﹣1,﹣1);②图象经过第一、二、四象限;③当x>1时,y<0;④y的值随着x值的增大而增大,以上结论正确的个数是( )
A.0个
B.1个
C.2个
D.3个
【解答】解:①当x=﹣1时,y=﹣3+2=﹣1,故正确;
②k=3>0,b=2>0,故图象经过第一、二、三象限,故错误;
③y=0时,x,故x时,y<0,故错误;
④k=3>0,故y的值随着x值的增大而增大,正确;
故选:C.
【点评】本题考查的是一次函数图象上点的坐标特征,由k值的符号,确定函数的增减性即可求解.
二、填空题
11.(4分)8的立方根是 2 .
【解答】解:8的立方根为2,
故答案为:2.
【点评】此题考查了立方根,熟练掌握立方根的定义是解本题的关键.
12.(4分)6
=13.(4分)一次函数的图象不经过第________象限
【解答】故答案为:三.
【点评】本题考查了点的坐标,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
14.(4分)若函数y=2x+(1﹣m)是正比例函数,则m的值是 1 .
【解答】解:∵函数y=2x+(1﹣m)是正比例函数,
∴1﹣m=0,
解得:m=1.
故答案为:1.
【点评】此题主要考查了正比例函数的定义,正确掌握正比例函数的定义是解题关键.
三、解答题
15.(20分)计算
(1)化简:
(2)化简:
16.(1)解方程:
(2)解方程:
17.(8分)先化简,再求值:(2a﹣3)(a+1)﹣a(a﹣3),其中a1.
【解答】解:(2a﹣3)(a+1)﹣a(a﹣3)
=2a2﹣a﹣3﹣a2+3a
=a2+2a﹣3,
当a1时,原式=(1)2+2(1)﹣3=2﹣21+22﹣3=﹣2.
【点评】本题考查整式的混合运算﹣化简求值,解答本题的关键是明确整式化简求值的方法.
18.(8分)△ABC在直角坐标系内的位置如图.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标.
【解答】解:(1)A(0,3),B(﹣4,4),C(﹣2,1);
(2)△A1B1C1如图所示,B1(4,4).
【点评】本题考查了利用轴对称作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.
19.
【解答】解:
2x2﹣xy+2y2
=2(x﹣y)2+3xy
=2×()2+3
=2×1+3
=2
.
(10分)略
八上数学期中B卷
参考答案与试题解析
一、填空题
21.(4分)已知2a﹣1的平方根是±3,3a﹣b﹣1的立方根是2,a+b的平方根 ± .
【解答】解:由题意,有,
解得.
则a+b=5+6=11,
所以a+b的平方根±.
故答案为:±.
【点评】本题考查了平方根、立方根的定义.解题的关键是掌握平方根、立方根的定义.如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.如果一个数x的立方等于a,那么这个数x就叫做a的立方根.
22.(4分)已知点A(m﹣5,1),点B(4,m+1),且直线AB∥y轴,则m= 9 .
【解答】解:∵点A(m﹣5,1),点B(4,m+1),且直线AB∥y轴,
∴m﹣5=4,
解得m=9.
故答案是:9.
【点评】本题考查了坐标与图形性质.需要掌握平行于坐标轴直线上点的坐标特征.
23.(4分)如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AD是∠BAC的平分线.若P、Q分别是AD和AC上的动点,则PC+PQ的最小值是 .
【解答】解:过点D作DE⊥AB于点E,过点E作EQ⊥AC于点Q,EQ交AD于点P,连接CP,此时PC+PQ=EQ取最小值,如图所示.
在Rt△ABC中,∠ACB=90°,AC=9,BC=12,
∴AB═15.
∵AD是∠BAC的平分线,
∴∠CAD=∠EAD,
在△ACD和△AED中,
∴△ACD≌△AED(AAS),
∴AE=AC=9.
∵EQ⊥AC,∠ACB=90°,
∴EQ∥BC,
∴,
即,
∴EQ,
故答案为.
【点评】本题考查了勾股定理、轴对称中的最短路线问题以及平行线的性质,找出点P、Q的位置是解题的关键.
4.(4分)若xy=5,x+y=﹣6,则 .
【解答】解:∵xy=5,x+y=﹣6,
∴x<0,y<0,
∴(),
故答案为:.
【点评】本题考查的是二次根式的化简求值,掌握二次根式的混合运算法则是解题的关键.
5.(4分)在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn,则Sn的值为 22n﹣3 (用含n的代数式表示,n为正整数).
【解答】方法一:
解:∵直线y=x+1,当x=0时,y=1,当y=0时,x=﹣1,
∴OA1=1,OD=1,
∴∠ODA1=45°,
∴∠A2A1B1=45°,
∴A2B1=A1B1=1,
∴S11×1,
∵A2B1=A1B1=1,
∴A2C1=2=21,
∴S2(21)2=21
同理得:A3C2=4=22,…,
S3(22)2=23
∴Sn(2n﹣1)2=22n﹣3
故答案为:22n﹣3.
方法二:
∵y=x+1,正方形A1B1C1O,
∴OA1=OC1=1,A2C1=2,B1C1=1,
∴A2B1=1,S1,
∵OC2=1+2=3,
∴A3C2=4,B2C2=2,
∴A3B2=2,
S2=2,
∴q4,
∴Sn.
【点评】本题考查了一次函数图象上点的坐标特征以及正方形的性质;通过求出第一个正方形、第二个正方形和第三个正方形的边长得出规律是解决问题的关键.
二、解答题
26.(8分)已知点A(5,a)与点B(5,﹣3)关于x轴对称,b为1的小数部分,求
(1)a+b的值.
(2)化简(1)b.
【解答】解:(1∵点A(5,a)与点B(5,﹣3)关于x轴对称,
∴a=3.
∵12,
∴b1.
∴以a+b1+32.
(2)将a、b的值代入得:原式(1)(1)=22﹣1=+1.
【点评】本题主要考查的是二次根式的混合运算,熟练掌握运算法则是解题的关键.
27.(10分)如图①,在△ABC中,∠C=90°,分别以△ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3
(1)如图②,在△ABC中,∠C=90°,分别以△ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系:(不必证明)
(2)如图③,△ABC中,∠C=90°,分别以△ABC三边为边向外作三个正三角形,其面积分别用S1,S2,S3表示,请你确定S1,S2,S3之间的关系并加以证明
(3)利用图①的结论,解决下列问题:如图④,Rt△ABC中,∠C=90°,AC=5,BC=8.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1,S2,S3,S4.则S1+S2+S3+S4= 60 .
【解答】解:(1)如图(2),分别以Rt△ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,那么S1=S2+S3,
理由为:在Rt△ABC中,利用勾股定理得:AB2=AC2+BC2,
∴AB2AC2BC2,即S1=S2+S3;
(2)如图(3),分别以Rt△ABC三边为边向外作三个正三角形,其面积分别用
S1、S2、S3表示,S1、S2、S3之间的关系为S1=S2+S3,
理由为:在Rt△ABC中,利用勾股定理得:AB2=AC2+BC2,
∴AB2AC2BC2,即S1=S2+S3;
(3)过F作AM的垂线交AM于D,
∴DF∥PC,
可证明Rt△ADF≌Rt△ABC,Rt△DFK≌Rt△CAT,
所以FD=AC=CP,
∴四边形CDFP是矩形,
∴∠CPF=90°,
∵∠QPC=90°,
∴∠QPF=180°,
∴Q,P,F三点共线,S2=SRt△ABC.
由Rt△DFK≌Rt△CAT可进一步证得:Rt△FPT≌Rt△EMK,
∴S3=S△FPT,
又可证得Rt△AQF≌Rt△ACB,
∴S1+S3=SRt△AQF=SRt△ABC.
易证Rt△ABC≌Rt△EBN,
∴S4=SRt△ABC,
∴S1+S2+S3+S4
=(S1+S3)+S2+S4
=SRt△ABC+SRt△ABC+SRt△ABC
=SRt△ABC×3
=5×8÷2×3
=60.
同课章节目录
