二次函数综合题(共38张ppt)
图片预览










文档简介
(共38张PPT)
第五节 二次函数的应用
1.为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于300元,那么政府为他承担的总差价最少为多少元?
考点一
二次函数的实际应用
考点二
二次函数的综合应用
命题角度? 线段、周长问题
例2
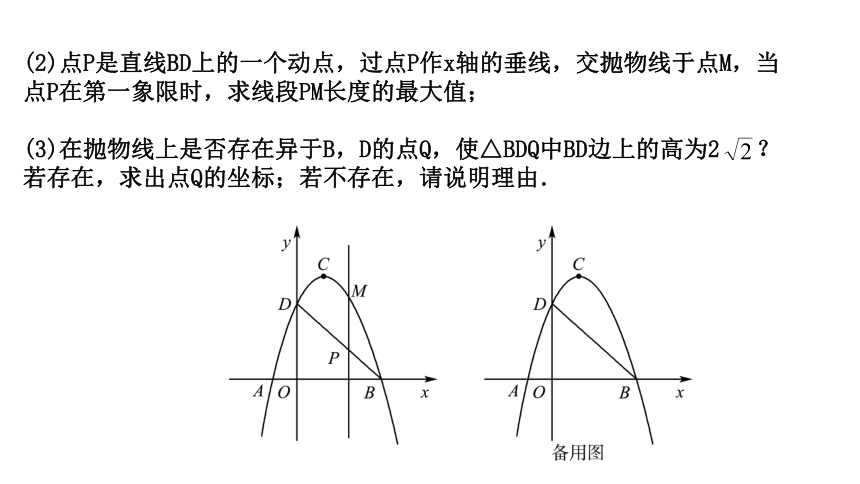
(2019·肥城二模)如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴
于A,B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的表达式和直线BD的表达式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当
点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B,D的点Q,使△BDQ中BD边上的高为2
?
若存在,求出点Q的坐标;若不存在,请说明理由.
【分析】(1)利用顶点式求得二次函数的表达式,再求出点D的坐标,即可
求得直线BD的表达式;
(2)设P点横坐标为m,则P(m,-m+3),M(m,-m2+2m+3),可得PM=-
M2+3m=-(m-
)2+
,即可得解;
(3)过Q作QE⊥x轴,交BD于点G,交x轴于点E,作QH⊥BD于H,连接QD,
QB,设Q(x,-x2+2x+3),G(x,-x+3),可得QG,利用等腰直角三角
形的性质、根的判别式,即可得解.
【自主解答】(1)∵抛物线的顶点C的坐标为(1,4),
∴可设抛物线表达式为y=a(x-1)2+4.
把B(3,0)代入得0=a(3-1)2+4,解得a=-1,
∴抛物线表达式为y=-(x-1)2+4,即y=-x2+2x+3.
∵点D在y轴上,令x=0可得y=3,
∴D点坐标为(0,3),
∴可设直线BD表达式为y=kx+3.
把B点坐标代入可得3k+3=0,解得k=-1,
∴直线BD表达式为y=-x+3.
(2)设P点横坐标为m(m>0),则P(m,-m+3),M(m,-m2+2m+3),
∴PM=-m2+2m+3-(-m+3)=-m2+3m=-(m-
)2+
,
∴当m=
时,PM有最大值,最大值为
.
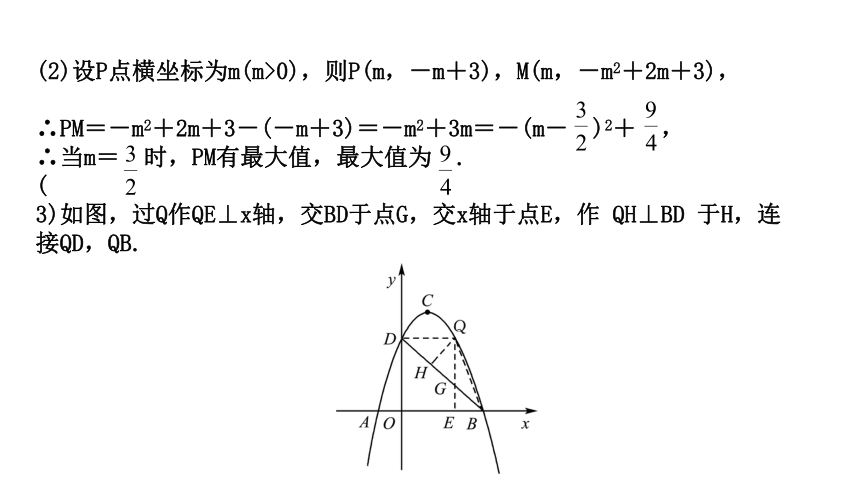
(
3)如图,过Q作QE⊥x轴,交BD于点G,交x轴于点E,作
QH⊥BD
于H,连
接QD,QB.
设Q(x,-x2+2x+3),则G(x,-x+3),
∴QG=|-x2+2x+3-(-x+3)|=|-x2+3x|.
∵△BOD是等腰直角三角形,
∴∠DBO=45°,
∴∠HGQ=∠BGE=45°.
当△BDQ中BD边上的高为2
时,
即QH=HG=2
,
∴QG=
×2
=4,
∴|-x2+3x|=4,
当-x2+3x=4时,Δ=9-16<0,方程无实数根,
当-x2+3x=-4时,解得x=-1或x=4,
∴Q(-1,0)或(4,-5).
综上可知,存在满足条件的点Q,其坐标为(-1,0)或(4,-5).
2.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)试求抛物线的解析式;
(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=
,试求m的最大值及此时点P的坐标;
(3)在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.
y=﹣
x2+x+4
3.(2018·泰安模拟)如图,抛物线y=ax2+bx+2与x轴交于A,B两点,
与y轴交于点C,AB=4.矩形OADC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的表达式;
(2)点P是直线EO上方抛物线上的一个动点,作PH⊥EO,垂足为H,求PH的
最大值;
(3)点M在抛物线上,点N在抛物线的对称轴上,若四边形ACMN是平行四边
形,求点M,N的坐标.
解:(1)将x=0代入抛物线的表达式得y=2,
∴C(0,2).
∵四边形OADC为矩形,∴OA=CD=1,
∴A(-1,0).
又∵AB=4,∴B(3,0).
设抛物线的表达式为y=a(x-3)(x+1).
将点C的坐标代入得-3a=2,解得a=-
,
∴抛物线的表达式为y=-
x2+
x+2.
(2)∵点E在DC的延长线上,∴y=2.
将y=2代入二次函数表达式得-
x2+
x+2=2,
解得x1=0(舍去),x2=2,
∴E(2,2),∴EC=OC=2,∴∠COE=45°.
如图,过点P作PG∥y轴交直线OE于点G,
∴∠PGH=∠COE=45°.
又∵PH⊥OE,∴PH=
PG.
设直线OE的表达式为y=kx,将点E的坐标代入得2k=2,
解得k=1,
∴直线OE的表达式为y=x,
∴设点P的坐标为(m,-
m2+
m+2),则点G的坐标为(m,m),
∴PH的最大值为
(3)由(1)可得抛物线的对称轴为x=1,
设点N的坐标为(1,n),点M的坐标为(e,f).
过点M作MQ垂直于对称轴,垂足为Q.
由AAS易证△MNQ≌△ACO,
∴QN=OC=2,MQ=AO=1,
∴点M的横坐标为2.
代入抛物线y=-
x2+
x+2得
Y=-
×4+
×2+2=2,
∴点M的坐标为(2,2),∴N的纵坐标为0,
∴点N的坐标为(1,0).
考点三
二次函数的综合应用
1.若一次函数
的图象与
轴,
轴分别交于
,
两点,点
的坐标为
,二次函数的
图象过
,
,
三点,如图
(1)求二次函数的表达式;
(2)如图(1),过点
作
轴交抛物线于点
,点
在抛物线上(
轴左侧),若
恰好平分
.求直线
的表达式;
(3)如图(2),若点
在抛物线上(点
在轴右侧),连接
交
于点
,连接
,
.
①当
时,求点
的坐标;
②求
的最大值.
1.如图,直线y=
x+2与x轴,y轴分别交于点A,C,抛物线y=﹣
x2+bx+c经过A,C两点,与x轴的另一交点为B.点D是AC上方抛物线上一点.
(1)求抛物线的函数表达式;
(2)连接BC,CD,设直线BD交线段AC于点E,如图1,△CDE,△BCE的面积分别为S1,S2,求
的最大值;
(3)过点D作DF⊥AC于F,连接CD,如图2,是否存在点D,使得△CDF中的某个角等于∠BAC的两倍?若存在,求点D的横坐标;若不存在,说明理由.
y=﹣
x2﹣
x+2;
1.如图,在平面直角坐标系xOy中,已知抛物线y=
+bx+c与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且
.
(1)求这条抛物线的表达式,并写出它的对称轴;
(2)求∠FAB的余切值;
(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.
2.如图,抛物线y=x2+bx+c与x轴交于A(1,0),B(﹣3,0),与y轴交于C
(1)求该抛物线的解析式,并写出抛物线的对称轴;
(2)设抛物线的对称轴交x轴于D,在对称轴左侧的抛物线上有一点E,使S△ACE=
,求点E的坐标;
(3)若P是直线y=x+1上的一点,P点的横坐标为
,M是第二象限抛物线上的一点,当∠MPD=∠ADC时,求M点的坐标.
y=(x﹣1)(x+3)=x2+2x﹣3.
3.2019秋?肥城市期末)如图,抛物线y=﹣x2+bx+c交x轴于A,B两点,交y轴于点C,直线y=﹣
x+2经过点B,C.
(1)求抛物线的解析式;
(2)点P是直线BC上方抛物线上一动点,设点P的横坐标为m.求△PBC面积最大值和此时m的值;
(3)Q是抛物线上一点,若∠ABC=∠CBQ,直线BQ与y轴交于点M,请直接写出M的坐标.
命题角度? 图形面积问题
例3
(2018·泰安中考)如图,在平面直角坐标系中,二次函数y=ax2+bx
+c交x轴于点A(-4,0),B(2,0),交y轴于点C(0,6),在y轴上有一点
E(0,-2),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形,若存在,请直
接写出所有P点的坐标;若不存在,请说明理由.
【分析】(1)把已知点坐标代入函数表达式,得出方程组求解即可;
(2)根据函数表达式设出点D坐标,过点D作DH与y轴平行,交AE于点F,表
示出△ADE的面积,运用二次函数分析最值即可;
(3)设出点P坐标,分PA=PE,PA=AE,PE=AE三种情况讨论分析即可.
【自主解答】(1)由题意可得
∴二次函数的表达式为y=-
x2-
x+6.
(2)由A(-4,0),E(0,-2),
可求得AE所在直线表达式为
y=-
x-2.
如图,过点D作DH与y轴平行,交AE于点F,
交x轴于点G,过点E作EH⊥DF,垂足为H.
设D点坐标为(x0,-
x02-
x0+6),则F点坐标为(x0,-
x0-2),
则DF=-
x02-
x0+6-(-
x0-2)=-
x02-x0+8.
又∵S△ADE=
S△ADF+
S△EDF,
∴S△ADE=DF·AG+DF·EH
=
×4DF
=2×(-
x02-x0+8)
=-
(x0+
)2+
,
∴当x0=-
时,△ADE的面积取得最大值
.
(3)P点的坐标为(-1,1),(-1,±
),(-1,-2±
).
2.(2019·泰安中考)若二次函数y=ax2+bx+c的图象与x轴、y轴分别交
于点A(3,0),B(0,-2),且过点C(2,-2).
(1)求二次函数表达式;
(2)若点P为抛物线上第一象限内的点,且S△PBA=4,求点P的坐标;
(3)在抛物线上(AB下方)是否存在点M,使∠ABO=∠ABM?若存在,求出点
M到y轴的距离;若不存在,请说明理由.
3.如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=﹣x2+bx+c.点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.
(1)求抛物线的解析式.
(2)当DE=4时,求四边形CAEB的面积.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求此点D坐标;若不存在,说明理由.
4.如图1,在平面直角坐标系中,直线y=x﹣1与抛物线y=﹣x2+bx+c交于A、B两点,其中A(m,0)、B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D.
(1)求m、n的值及该抛物线的解析式;
(2)如图2,若点P为线段AD上的一动点(不与A、D重合),分别以AP、DP为斜边,在直线AD的同侧作等腰直角△APM和等腰直角△DPN,连接MN,试确定△MPN面积最大时P点的坐标;
(3)如图3,连接BD、CD,在线段CD上是否存在点Q,使得以A、D、Q为顶点的三角形与△ABD相似,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
y=﹣x2+6x﹣5;
5.如图,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1,x2是方程x2﹣2x﹣8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
命题角度? 动点、存在点问题
例4
(2017·泰安中考)如图,是将抛物线y=-x2平移后得到的抛物线,
其对称轴为x=1,与x轴的一个交点为A(-1,0),
另一交点为B,与y轴的交点为C.
(1)求抛物线的函数表达式;
(2)若点N为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=
x+
的图象上一点,若四
边形OAPQ为平行四边形,这样的点P,Q是否存在?若存在,分别求出点
P,Q的坐标;若不存在,说明理由.
【分析】(1)设出顶点式,利用待定系数法求函数表达式;
(2)易证△BOC是等腰直角三角形,过点N作NH⊥y轴,根据CH=NH即可列方
程求解;
(3)四边形OAPQ是平行四边形,则PQ=OA=1,且PQ∥OA,设P点坐标,代
入y=
x+
即可求解.
【自主解答】(1)设抛物线的表达式为y=-(x-1)2+k.
∵A(-1,0)在抛物线上,
∴0=-(-1-1)2+k,∴k=4,
∴抛物线的表达式为y=-(x-1)2+4=-x2+2x+3.
(2)当x=0时,y=-(0-1)2+4=3,
∴点C(0,3),∴OC=3.
又B(3,0),∴△BOC为等腰直角三角形,
∴∠OCB=45°.
如图,过点N作NH⊥y轴,垂足为H.
∵∠NCB=90°,∴∠NCH=45°,
∴NH=CH,
∴HO=OC+CH=3+CH=3+NH,
则设点N为(a,-a2+2a+3),
∴a+3=-a2+2a+3,
解得a=0(舍去)或a=1,
∴N(1,4).
(3)∵四边形OAPQ是平行四边形,则PQ=OA=1,
且PQ∥OA,
设P(t,-t2+2t+3),则Q(t+1,-t2+2t+3).
将点Q(t+1,-t2+2t+3)代入y=
x+
得
-t2+2t+3=
(t+1)+
,
整理得2t2-t=0,解得t1=0,t2=
.
∴-t2+2t+3的值为3或
,
∴点P,Q的坐标为(0,3),(1,3)或(
,
),(
,
).
1.如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C
(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,且以AO为边的四边形AODE是平行四边形,求点D的坐标.
(3)P是抛物线上第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
2(2016?潍坊)如图,已知抛物线y=
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的点.
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
y=
x2+2x+1,
3.如图,直线y=﹣x+3与x轴、y轴分别相交x轴于点B、交y轴于点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
(1)求A点的坐标;
(2)求该抛物线的函数表达式;
(3)连接AC.请问在x轴上是否存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
y=x2﹣4x+3.
第五节 二次函数的应用
1.为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于300元,那么政府为他承担的总差价最少为多少元?
考点一
二次函数的实际应用
考点二
二次函数的综合应用
命题角度? 线段、周长问题
例2
(2019·肥城二模)如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴
于A,B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).
(1)求二次函数的表达式和直线BD的表达式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当
点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B,D的点Q,使△BDQ中BD边上的高为2
?
若存在,求出点Q的坐标;若不存在,请说明理由.
【分析】(1)利用顶点式求得二次函数的表达式,再求出点D的坐标,即可
求得直线BD的表达式;
(2)设P点横坐标为m,则P(m,-m+3),M(m,-m2+2m+3),可得PM=-
M2+3m=-(m-
)2+
,即可得解;
(3)过Q作QE⊥x轴,交BD于点G,交x轴于点E,作QH⊥BD于H,连接QD,
QB,设Q(x,-x2+2x+3),G(x,-x+3),可得QG,利用等腰直角三角
形的性质、根的判别式,即可得解.
【自主解答】(1)∵抛物线的顶点C的坐标为(1,4),
∴可设抛物线表达式为y=a(x-1)2+4.
把B(3,0)代入得0=a(3-1)2+4,解得a=-1,
∴抛物线表达式为y=-(x-1)2+4,即y=-x2+2x+3.
∵点D在y轴上,令x=0可得y=3,
∴D点坐标为(0,3),
∴可设直线BD表达式为y=kx+3.
把B点坐标代入可得3k+3=0,解得k=-1,
∴直线BD表达式为y=-x+3.
(2)设P点横坐标为m(m>0),则P(m,-m+3),M(m,-m2+2m+3),
∴PM=-m2+2m+3-(-m+3)=-m2+3m=-(m-
)2+
,
∴当m=
时,PM有最大值,最大值为
.
(
3)如图,过Q作QE⊥x轴,交BD于点G,交x轴于点E,作
QH⊥BD
于H,连
接QD,QB.
设Q(x,-x2+2x+3),则G(x,-x+3),
∴QG=|-x2+2x+3-(-x+3)|=|-x2+3x|.
∵△BOD是等腰直角三角形,
∴∠DBO=45°,
∴∠HGQ=∠BGE=45°.
当△BDQ中BD边上的高为2
时,
即QH=HG=2
,
∴QG=
×2
=4,
∴|-x2+3x|=4,
当-x2+3x=4时,Δ=9-16<0,方程无实数根,
当-x2+3x=-4时,解得x=-1或x=4,
∴Q(-1,0)或(4,-5).
综上可知,存在满足条件的点Q,其坐标为(-1,0)或(4,-5).
2.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)试求抛物线的解析式;
(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=
,试求m的最大值及此时点P的坐标;
(3)在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.
y=﹣
x2+x+4
3.(2018·泰安模拟)如图,抛物线y=ax2+bx+2与x轴交于A,B两点,
与y轴交于点C,AB=4.矩形OADC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的表达式;
(2)点P是直线EO上方抛物线上的一个动点,作PH⊥EO,垂足为H,求PH的
最大值;
(3)点M在抛物线上,点N在抛物线的对称轴上,若四边形ACMN是平行四边
形,求点M,N的坐标.
解:(1)将x=0代入抛物线的表达式得y=2,
∴C(0,2).
∵四边形OADC为矩形,∴OA=CD=1,
∴A(-1,0).
又∵AB=4,∴B(3,0).
设抛物线的表达式为y=a(x-3)(x+1).
将点C的坐标代入得-3a=2,解得a=-
,
∴抛物线的表达式为y=-
x2+
x+2.
(2)∵点E在DC的延长线上,∴y=2.
将y=2代入二次函数表达式得-
x2+
x+2=2,
解得x1=0(舍去),x2=2,
∴E(2,2),∴EC=OC=2,∴∠COE=45°.
如图,过点P作PG∥y轴交直线OE于点G,
∴∠PGH=∠COE=45°.
又∵PH⊥OE,∴PH=
PG.
设直线OE的表达式为y=kx,将点E的坐标代入得2k=2,
解得k=1,
∴直线OE的表达式为y=x,
∴设点P的坐标为(m,-
m2+
m+2),则点G的坐标为(m,m),
∴PH的最大值为
(3)由(1)可得抛物线的对称轴为x=1,
设点N的坐标为(1,n),点M的坐标为(e,f).
过点M作MQ垂直于对称轴,垂足为Q.
由AAS易证△MNQ≌△ACO,
∴QN=OC=2,MQ=AO=1,
∴点M的横坐标为2.
代入抛物线y=-
x2+
x+2得
Y=-
×4+
×2+2=2,
∴点M的坐标为(2,2),∴N的纵坐标为0,
∴点N的坐标为(1,0).
考点三
二次函数的综合应用
1.若一次函数
的图象与
轴,
轴分别交于
,
两点,点
的坐标为
,二次函数的
图象过
,
,
三点,如图
(1)求二次函数的表达式;
(2)如图(1),过点
作
轴交抛物线于点
,点
在抛物线上(
轴左侧),若
恰好平分
.求直线
的表达式;
(3)如图(2),若点
在抛物线上(点
在轴右侧),连接
交
于点
,连接
,
.
①当
时,求点
的坐标;
②求
的最大值.
1.如图,直线y=
x+2与x轴,y轴分别交于点A,C,抛物线y=﹣
x2+bx+c经过A,C两点,与x轴的另一交点为B.点D是AC上方抛物线上一点.
(1)求抛物线的函数表达式;
(2)连接BC,CD,设直线BD交线段AC于点E,如图1,△CDE,△BCE的面积分别为S1,S2,求
的最大值;
(3)过点D作DF⊥AC于F,连接CD,如图2,是否存在点D,使得△CDF中的某个角等于∠BAC的两倍?若存在,求点D的横坐标;若不存在,说明理由.
y=﹣
x2﹣
x+2;
1.如图,在平面直角坐标系xOy中,已知抛物线y=
+bx+c与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且
.
(1)求这条抛物线的表达式,并写出它的对称轴;
(2)求∠FAB的余切值;
(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.
2.如图,抛物线y=x2+bx+c与x轴交于A(1,0),B(﹣3,0),与y轴交于C
(1)求该抛物线的解析式,并写出抛物线的对称轴;
(2)设抛物线的对称轴交x轴于D,在对称轴左侧的抛物线上有一点E,使S△ACE=
,求点E的坐标;
(3)若P是直线y=x+1上的一点,P点的横坐标为
,M是第二象限抛物线上的一点,当∠MPD=∠ADC时,求M点的坐标.
y=(x﹣1)(x+3)=x2+2x﹣3.
3.2019秋?肥城市期末)如图,抛物线y=﹣x2+bx+c交x轴于A,B两点,交y轴于点C,直线y=﹣
x+2经过点B,C.
(1)求抛物线的解析式;
(2)点P是直线BC上方抛物线上一动点,设点P的横坐标为m.求△PBC面积最大值和此时m的值;
(3)Q是抛物线上一点,若∠ABC=∠CBQ,直线BQ与y轴交于点M,请直接写出M的坐标.
命题角度? 图形面积问题
例3
(2018·泰安中考)如图,在平面直角坐标系中,二次函数y=ax2+bx
+c交x轴于点A(-4,0),B(2,0),交y轴于点C(0,6),在y轴上有一点
E(0,-2),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形,若存在,请直
接写出所有P点的坐标;若不存在,请说明理由.
【分析】(1)把已知点坐标代入函数表达式,得出方程组求解即可;
(2)根据函数表达式设出点D坐标,过点D作DH与y轴平行,交AE于点F,表
示出△ADE的面积,运用二次函数分析最值即可;
(3)设出点P坐标,分PA=PE,PA=AE,PE=AE三种情况讨论分析即可.
【自主解答】(1)由题意可得
∴二次函数的表达式为y=-
x2-
x+6.
(2)由A(-4,0),E(0,-2),
可求得AE所在直线表达式为
y=-
x-2.
如图,过点D作DH与y轴平行,交AE于点F,
交x轴于点G,过点E作EH⊥DF,垂足为H.
设D点坐标为(x0,-
x02-
x0+6),则F点坐标为(x0,-
x0-2),
则DF=-
x02-
x0+6-(-
x0-2)=-
x02-x0+8.
又∵S△ADE=
S△ADF+
S△EDF,
∴S△ADE=DF·AG+DF·EH
=
×4DF
=2×(-
x02-x0+8)
=-
(x0+
)2+
,
∴当x0=-
时,△ADE的面积取得最大值
.
(3)P点的坐标为(-1,1),(-1,±
),(-1,-2±
).
2.(2019·泰安中考)若二次函数y=ax2+bx+c的图象与x轴、y轴分别交
于点A(3,0),B(0,-2),且过点C(2,-2).
(1)求二次函数表达式;
(2)若点P为抛物线上第一象限内的点,且S△PBA=4,求点P的坐标;
(3)在抛物线上(AB下方)是否存在点M,使∠ABO=∠ABM?若存在,求出点
M到y轴的距离;若不存在,请说明理由.
3.如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=﹣x2+bx+c.点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.
(1)求抛物线的解析式.
(2)当DE=4时,求四边形CAEB的面积.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求此点D坐标;若不存在,说明理由.
4.如图1,在平面直角坐标系中,直线y=x﹣1与抛物线y=﹣x2+bx+c交于A、B两点,其中A(m,0)、B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D.
(1)求m、n的值及该抛物线的解析式;
(2)如图2,若点P为线段AD上的一动点(不与A、D重合),分别以AP、DP为斜边,在直线AD的同侧作等腰直角△APM和等腰直角△DPN,连接MN,试确定△MPN面积最大时P点的坐标;
(3)如图3,连接BD、CD,在线段CD上是否存在点Q,使得以A、D、Q为顶点的三角形与△ABD相似,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
y=﹣x2+6x﹣5;
5.如图,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1,x2是方程x2﹣2x﹣8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
命题角度? 动点、存在点问题
例4
(2017·泰安中考)如图,是将抛物线y=-x2平移后得到的抛物线,
其对称轴为x=1,与x轴的一个交点为A(-1,0),
另一交点为B,与y轴的交点为C.
(1)求抛物线的函数表达式;
(2)若点N为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=
x+
的图象上一点,若四
边形OAPQ为平行四边形,这样的点P,Q是否存在?若存在,分别求出点
P,Q的坐标;若不存在,说明理由.
【分析】(1)设出顶点式,利用待定系数法求函数表达式;
(2)易证△BOC是等腰直角三角形,过点N作NH⊥y轴,根据CH=NH即可列方
程求解;
(3)四边形OAPQ是平行四边形,则PQ=OA=1,且PQ∥OA,设P点坐标,代
入y=
x+
即可求解.
【自主解答】(1)设抛物线的表达式为y=-(x-1)2+k.
∵A(-1,0)在抛物线上,
∴0=-(-1-1)2+k,∴k=4,
∴抛物线的表达式为y=-(x-1)2+4=-x2+2x+3.
(2)当x=0时,y=-(0-1)2+4=3,
∴点C(0,3),∴OC=3.
又B(3,0),∴△BOC为等腰直角三角形,
∴∠OCB=45°.
如图,过点N作NH⊥y轴,垂足为H.
∵∠NCB=90°,∴∠NCH=45°,
∴NH=CH,
∴HO=OC+CH=3+CH=3+NH,
则设点N为(a,-a2+2a+3),
∴a+3=-a2+2a+3,
解得a=0(舍去)或a=1,
∴N(1,4).
(3)∵四边形OAPQ是平行四边形,则PQ=OA=1,
且PQ∥OA,
设P(t,-t2+2t+3),则Q(t+1,-t2+2t+3).
将点Q(t+1,-t2+2t+3)代入y=
x+
得
-t2+2t+3=
(t+1)+
,
整理得2t2-t=0,解得t1=0,t2=
.
∴-t2+2t+3的值为3或
,
∴点P,Q的坐标为(0,3),(1,3)或(
,
),(
,
).
1.如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C
(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,且以AO为边的四边形AODE是平行四边形,求点D的坐标.
(3)P是抛物线上第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
2(2016?潍坊)如图,已知抛物线y=
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的点.
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
y=
x2+2x+1,
3.如图,直线y=﹣x+3与x轴、y轴分别相交x轴于点B、交y轴于点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
(1)求A点的坐标;
(2)求该抛物线的函数表达式;
(3)连接AC.请问在x轴上是否存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
y=x2﹣4x+3.
