2020-2021学年青岛新版七年级上册数学《第1章 基本的几何图形》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年青岛新版七年级上册数学《第1章 基本的几何图形》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 208.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-19 20:27:02 | ||
图片预览


文档简介
2020-2021学年青岛新版七年级上册数学《第1章
基本的几何图形》单元测试卷
一.选择题
1.下列立体图形中,面数相同的是( )
①正方体;②圆柱;③四棱柱;④圆锥.
A.①②
B.①③
C.②③
D.③④
2.用圆规画圆的过程中,把圆规的两脚分开,定好两脚间的距离是3cm,则该圆的直径是( )cm.
A.1.5
B.3
C.4.5
D.6
3.如图,长方形的长为3cm、宽为2cm,分别以该长方形的长、宽所在直线为轴,将其旋转1周,形成甲、乙两个圆柱,其体积分别记作V甲、V乙,侧面积分别记作S甲、S乙,则下列说法正确的是( )
A.V甲<V乙,S甲=S乙
B.V甲>V乙,S甲>S乙
C.V甲=V乙,S甲=S乙
D.V甲>V乙,S甲<S乙
4.如图,从A到B有①,②,③三条路线,最短的路线是①,其理由是( )
A.因为它最直
B.两点确定一条直线
C.两点间的距离的概念
D.两点之间,线段最短
5.如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )
A.CD=AC﹣BD
B.CD=BC
C.CD=AB﹣BD
D.CD=AD﹣BC
6.电视剧《西游记》中,孙悟空的“金箍棒”飞速旋转,形成一个圆面,是属于( )
A.点动成线
B.线动成面
C.面动成体
D.以上都不对
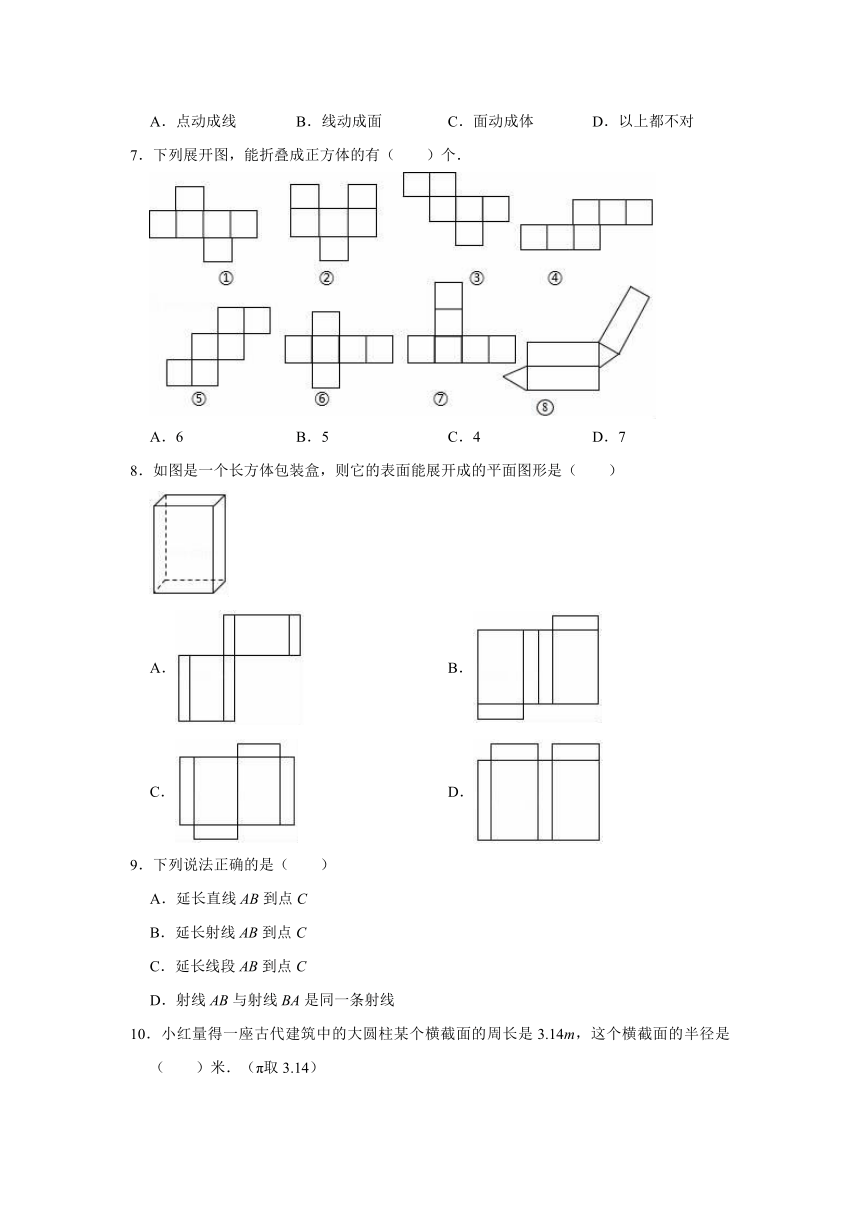
7.下列展开图,能折叠成正方体的有( )个.
A.6
B.5
C.4
D.7
8.如图是一个长方体包装盒,则它的表面能展开成的平面图形是( )
A.
B.
C.
D.
9.下列说法正确的是( )
A.延长直线AB到点C
B.延长射线AB到点C
C.延长线段AB到点C
D.射线AB与射线BA是同一条射线
10.小红量得一座古代建筑中的大圆柱某个横截面的周长是3.14m,这个横截面的半径是( )米.(π取3.14)
A.3.14
B.2
C.1
D.
二.填空题
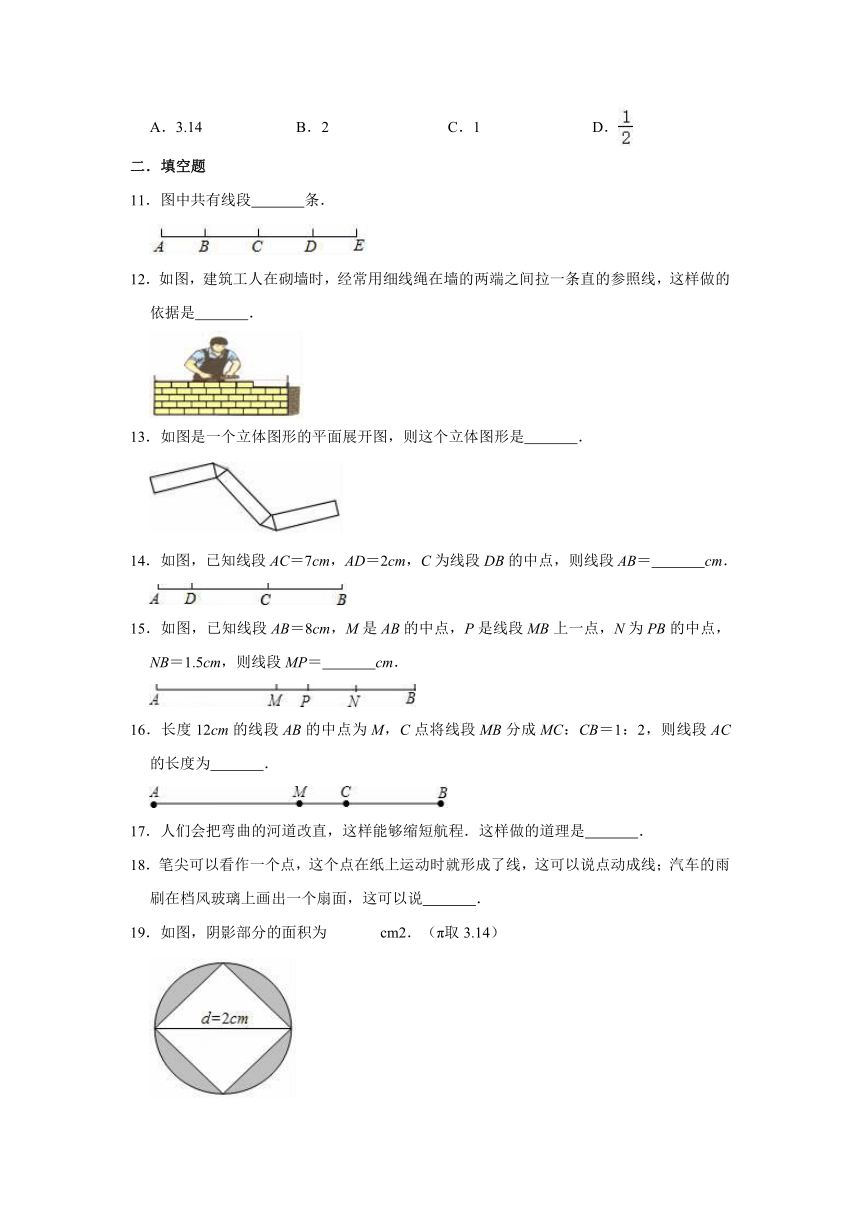
11.图中共有线段
条.
12.如图,建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条直的参照线,这样做的依据是
.
13.如图是一个立体图形的平面展开图,则这个立体图形是
.
14.如图,已知线段AC=7cm,AD=2cm,C为线段DB的中点,则线段AB=
cm.
15.如图,已知线段AB=8cm,M是AB的中点,P是线段MB上一点,N为PB的中点,NB=1.5cm,则线段MP=
cm.
16.长度12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段AC的长度为
.
17.人们会把弯曲的河道改直,这样能够缩短航程.这样做的道理是
.
18.笔尖可以看作一个点,这个点在纸上运动时就形成了线,这可以说点动成线;汽车的雨刷在档风玻璃上画出一个扇面,这可以说
.
19.如图,阴影部分的面积为
cm2.(π取3.14)
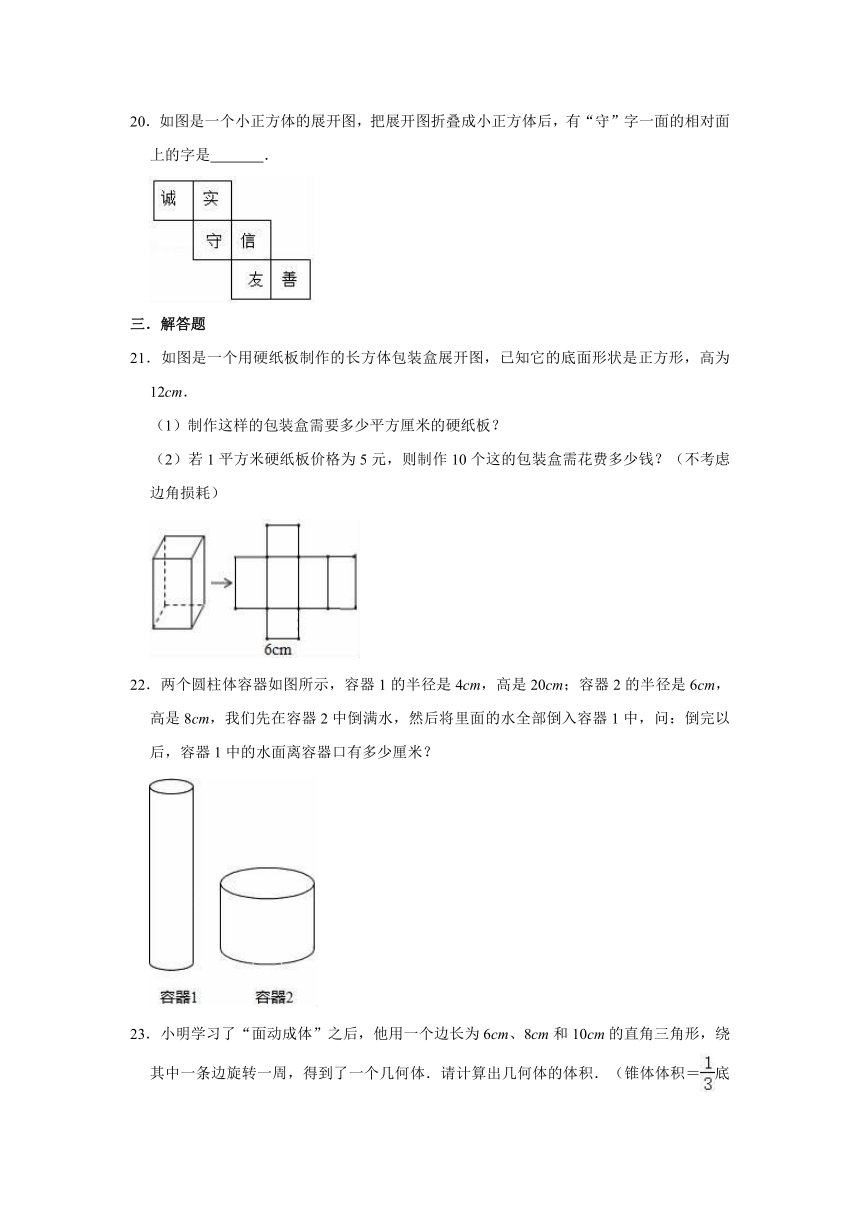
20.如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“守”字一面的相对面上的字是
.
三.解答题
21.如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)
22.两个圆柱体容器如图所示,容器1的半径是4cm,高是20cm;容器2的半径是6cm,高是8cm,我们先在容器2中倒满水,然后将里面的水全部倒入容器1中,问:倒完以后,容器1中的水面离容器口有多少厘米?
23.小明学习了“面动成体”之后,他用一个边长为6cm、8cm和10cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.(锥体体积=底面积×高)
24.点O是线段AB的中点,OB=14cm,点P将线段AB分为两部分,AP:PB=5:2.
①求线段OP的长.
②点M在线段AB上,若点M距离点P的长度为4cm,求线段AM的长.
25.我们知道,三棱柱的上、下底面都是三角形,那么正三棱柱的上、下底面都是等边三角形.如图,大正三棱柱的底面周长为10,截取一个底面周长为3的小正三棱柱.
(1)请写出截面的形状;
(2)请直接写出四边形DECB的周长.
26.过平面上四点中的任意两点作直线,甲说有一条,乙说有四条,丙说有六条,丁说他们说的都不对,应该是一条、四条或六条,谁说的对?请画图来说明你的看法.
27.如图已知点C为AB上一点,AC=18cm,CB=AC,D、E分别为AC、AB的中点,求DE的长.
参考答案与试题解析
一.选择题
1.解:①正方体六个面;
②圆柱三个面;
③四棱柱六个面;
④圆锥两个面,
面数相同的是①③,
故选:B.
2.解:∵把圆规的两脚分开,定好两脚间的距离是3cm,
∴该圆的直径是6cm,
故选:D.
3.解:由题可得,
V甲=π?22×3=12π,
V乙=π?32×2=18π,
∵12π<18π,
∴V甲<V乙;
∵S甲=2π×2×3=12π,
S乙=2π×3×2=12π,
∴S甲=S乙,
故选:A.
4.解:从A到B有①,②,③三条路线,最短的路线是①,其理由是:两点之间,线段最短,
故选:D.
5.解:∵C是线段AB的中点,
∴AC=BC=AB,
A、CD=BC﹣BD=AC﹣BD,故本选项正确;
B、D不一定是BC的中点,故CD=BC不一定成立;
C、CD=AD﹣AC=AD﹣BC,故本选项正确;
D、CD=BC﹣BD=AB﹣BD,故本选项正确.
故选:B.
6.解:孙悟空的“金箍棒”飞速旋转,形成一个圆面,是属于线动成面,
故选:B.
7.解:根据正方体展开图的特征可得,①③④⑤⑥可以折叠成正方体,而⑧折叠成三棱柱,
故选:B.
8.解:A、符合长方体的展开图的特点,是长方体的展开图,故此选项符合题意;
B、不符合长方体的展开图的特点,不是长方体的展开图,故此选项不符合题意;
C、不符合长方体的展开图的特点,不是长方体的展开图,故此选项不符合题意;
D、不符合长方体的展开图的特点,不是长方体的展开图,故此选项不符合题意.
故选:A.
9.解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;
B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;
C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;
D、射线AB与射线BA不是同一条射线,故本选项不符合题意;
故选:C.
10.解:设这个横截面的半径是r米,根据题意,得
2×3.14r=3.14,
解得r=,
故选:D.
二.填空题
11.解:由图得,图中的线段有:AB,BC,CD,DE,AC,BD,CE,BE,AD,AE一共10条.
故答案为:10.
12.解:建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.
故答案为:两点确定一条直线.
13.解:根据展开图可知,这个几何体两个底面是三角形,三个侧面是长方形的,因此这个几何体是三棱柱,
故答案为:三棱柱.
14.解:∵AC=7cm,AD=2cm,
∴CD=AC﹣AD=5cm,
∵C为线段DB的中点,
∴BC=CD=5cm,
∴AB=AC+BC=7+5=12(cm),
答:线段AB=12cm,
故答案为:12.
15.解:∵M是AB的中点,AB=8cm,
∴AM=BM=4cm,
∵N为PB的中点,NB=1.5cm,
∴PB=2NB=3cm,
∴MP=BM﹣PB=4﹣3=1cm.
故答案为1.
16.解:∵线段AB的中点为M,
∴AM=BM=6cm
设MC=x,则CB=2x,
∴x+2x=6,解得x=2
即MC=2cm.
∴AC=AM+MC=6+2=8cm.
17.解:由线段的性质可知,把弯曲的河道改直,能够缩短航程,这样做根据的道理是两点之间线段最短,
故答案为:两点之间线段最短.
18.解:汽车的雨刷实际上是一条线,通过运动把玻璃上的雨水刷干净,所以应是线动成面.
故答案为:线动成面.
19.解:S阴影=S圆形﹣S正方形=π×()2﹣×2×2=π﹣2≈1.14(cm2),
故答案为:1.14.
20.解:∵正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴“守”字一面的相对面上的字是“善”.
故答案为:善.
三.解答题
21.解:(1)由题意得,2×(12×6+12×6+6×6)=360cm2;
答:制作这样的包装盒需要360平方厘米的硬纸板;
(2)360÷10000×5×10=1.8元,
答:制作10个这的包装盒需花费1.8元钱.
22.解:设倒完以后,第一个容器中的水面离容器口有x
cm,
则:π×42×(20﹣x)=π×62×8,
解得:x=2,
答:第一个容器中的水面离容器口有2
cm.
23.解:以8cm为轴,得
以8cm为轴体积为×π×62×8=96π(cm3),
以6cm为轴,得
以6cm为轴的体积为×π×82×6=128π(cm3),
以10cm为轴,得
以10cm为轴的体积为×π()2×10=76.8π(cm3).
故几何体的体积为:96πcm3或128πcm3或76.8πcm3.
24.解:①∵点O是线段AB的中点,OB=14cm,
∴AB=2OB=28cm,
∵AP:PB=5:2.
∴BP=cm,
∴OP=OB﹣BP=14﹣8=6(cm);
②如图1,当M点在P点的左边时,
AM=AB﹣(PM+BP)=28﹣(4+8)=16(cm),
如图2,当M点在P点的右边时,
AM=AB﹣BM=AB﹣(BP﹣PM)=28﹣(8﹣4)=24(cm).
综上,AM=16cm或24cm.
25.解:(1)由题可得,截面的形状为长方形;
(2)∵△ADE是周长为3的等边三角形,
∴DE=AD=1,
又∵△ABC是周长为10的等边三角形,
∴AB=AC=BC=,
∴DB=EC=﹣1=,
∴四边形DECB的周长=1+×2+=9.
26.解:丁说的对.
(1)当四点共线时,可画1条,如图(1);
(2)当四点中有三点共线时,可画4条,如图(2);
(3)当四点中任意三点不共线时,可画6条,如图(3);
27.解:∵AC=18cm,CB=AC,
∴BC=×18=12cm,
则AB=AC+BC=30cm,
∵D、E分别为AC、AB的中点,
∴AD=AC=9cm,AE=AB=15cm,
∴DE=AE﹣AD=15﹣9=6cm,
答:DE的长是6cm.
基本的几何图形》单元测试卷
一.选择题
1.下列立体图形中,面数相同的是( )
①正方体;②圆柱;③四棱柱;④圆锥.
A.①②
B.①③
C.②③
D.③④
2.用圆规画圆的过程中,把圆规的两脚分开,定好两脚间的距离是3cm,则该圆的直径是( )cm.
A.1.5
B.3
C.4.5
D.6
3.如图,长方形的长为3cm、宽为2cm,分别以该长方形的长、宽所在直线为轴,将其旋转1周,形成甲、乙两个圆柱,其体积分别记作V甲、V乙,侧面积分别记作S甲、S乙,则下列说法正确的是( )
A.V甲<V乙,S甲=S乙
B.V甲>V乙,S甲>S乙
C.V甲=V乙,S甲=S乙
D.V甲>V乙,S甲<S乙
4.如图,从A到B有①,②,③三条路线,最短的路线是①,其理由是( )
A.因为它最直
B.两点确定一条直线
C.两点间的距离的概念
D.两点之间,线段最短
5.如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )
A.CD=AC﹣BD
B.CD=BC
C.CD=AB﹣BD
D.CD=AD﹣BC
6.电视剧《西游记》中,孙悟空的“金箍棒”飞速旋转,形成一个圆面,是属于( )
A.点动成线
B.线动成面
C.面动成体
D.以上都不对
7.下列展开图,能折叠成正方体的有( )个.
A.6
B.5
C.4
D.7
8.如图是一个长方体包装盒,则它的表面能展开成的平面图形是( )
A.
B.
C.
D.
9.下列说法正确的是( )
A.延长直线AB到点C
B.延长射线AB到点C
C.延长线段AB到点C
D.射线AB与射线BA是同一条射线
10.小红量得一座古代建筑中的大圆柱某个横截面的周长是3.14m,这个横截面的半径是( )米.(π取3.14)
A.3.14
B.2
C.1
D.
二.填空题
11.图中共有线段
条.
12.如图,建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条直的参照线,这样做的依据是
.
13.如图是一个立体图形的平面展开图,则这个立体图形是
.
14.如图,已知线段AC=7cm,AD=2cm,C为线段DB的中点,则线段AB=
cm.
15.如图,已知线段AB=8cm,M是AB的中点,P是线段MB上一点,N为PB的中点,NB=1.5cm,则线段MP=
cm.
16.长度12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段AC的长度为
.
17.人们会把弯曲的河道改直,这样能够缩短航程.这样做的道理是
.
18.笔尖可以看作一个点,这个点在纸上运动时就形成了线,这可以说点动成线;汽车的雨刷在档风玻璃上画出一个扇面,这可以说
.
19.如图,阴影部分的面积为
cm2.(π取3.14)
20.如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“守”字一面的相对面上的字是
.
三.解答题
21.如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)
22.两个圆柱体容器如图所示,容器1的半径是4cm,高是20cm;容器2的半径是6cm,高是8cm,我们先在容器2中倒满水,然后将里面的水全部倒入容器1中,问:倒完以后,容器1中的水面离容器口有多少厘米?
23.小明学习了“面动成体”之后,他用一个边长为6cm、8cm和10cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体.请计算出几何体的体积.(锥体体积=底面积×高)
24.点O是线段AB的中点,OB=14cm,点P将线段AB分为两部分,AP:PB=5:2.
①求线段OP的长.
②点M在线段AB上,若点M距离点P的长度为4cm,求线段AM的长.
25.我们知道,三棱柱的上、下底面都是三角形,那么正三棱柱的上、下底面都是等边三角形.如图,大正三棱柱的底面周长为10,截取一个底面周长为3的小正三棱柱.
(1)请写出截面的形状;
(2)请直接写出四边形DECB的周长.
26.过平面上四点中的任意两点作直线,甲说有一条,乙说有四条,丙说有六条,丁说他们说的都不对,应该是一条、四条或六条,谁说的对?请画图来说明你的看法.
27.如图已知点C为AB上一点,AC=18cm,CB=AC,D、E分别为AC、AB的中点,求DE的长.
参考答案与试题解析
一.选择题
1.解:①正方体六个面;
②圆柱三个面;
③四棱柱六个面;
④圆锥两个面,
面数相同的是①③,
故选:B.
2.解:∵把圆规的两脚分开,定好两脚间的距离是3cm,
∴该圆的直径是6cm,
故选:D.
3.解:由题可得,
V甲=π?22×3=12π,
V乙=π?32×2=18π,
∵12π<18π,
∴V甲<V乙;
∵S甲=2π×2×3=12π,
S乙=2π×3×2=12π,
∴S甲=S乙,
故选:A.
4.解:从A到B有①,②,③三条路线,最短的路线是①,其理由是:两点之间,线段最短,
故选:D.
5.解:∵C是线段AB的中点,
∴AC=BC=AB,
A、CD=BC﹣BD=AC﹣BD,故本选项正确;
B、D不一定是BC的中点,故CD=BC不一定成立;
C、CD=AD﹣AC=AD﹣BC,故本选项正确;
D、CD=BC﹣BD=AB﹣BD,故本选项正确.
故选:B.
6.解:孙悟空的“金箍棒”飞速旋转,形成一个圆面,是属于线动成面,
故选:B.
7.解:根据正方体展开图的特征可得,①③④⑤⑥可以折叠成正方体,而⑧折叠成三棱柱,
故选:B.
8.解:A、符合长方体的展开图的特点,是长方体的展开图,故此选项符合题意;
B、不符合长方体的展开图的特点,不是长方体的展开图,故此选项不符合题意;
C、不符合长方体的展开图的特点,不是长方体的展开图,故此选项不符合题意;
D、不符合长方体的展开图的特点,不是长方体的展开图,故此选项不符合题意.
故选:A.
9.解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;
B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;
C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;
D、射线AB与射线BA不是同一条射线,故本选项不符合题意;
故选:C.
10.解:设这个横截面的半径是r米,根据题意,得
2×3.14r=3.14,
解得r=,
故选:D.
二.填空题
11.解:由图得,图中的线段有:AB,BC,CD,DE,AC,BD,CE,BE,AD,AE一共10条.
故答案为:10.
12.解:建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上,沿着这条线就可以砌出直的墙,则其中的道理是:两点确定一条直线.
故答案为:两点确定一条直线.
13.解:根据展开图可知,这个几何体两个底面是三角形,三个侧面是长方形的,因此这个几何体是三棱柱,
故答案为:三棱柱.
14.解:∵AC=7cm,AD=2cm,
∴CD=AC﹣AD=5cm,
∵C为线段DB的中点,
∴BC=CD=5cm,
∴AB=AC+BC=7+5=12(cm),
答:线段AB=12cm,
故答案为:12.
15.解:∵M是AB的中点,AB=8cm,
∴AM=BM=4cm,
∵N为PB的中点,NB=1.5cm,
∴PB=2NB=3cm,
∴MP=BM﹣PB=4﹣3=1cm.
故答案为1.
16.解:∵线段AB的中点为M,
∴AM=BM=6cm
设MC=x,则CB=2x,
∴x+2x=6,解得x=2
即MC=2cm.
∴AC=AM+MC=6+2=8cm.
17.解:由线段的性质可知,把弯曲的河道改直,能够缩短航程,这样做根据的道理是两点之间线段最短,
故答案为:两点之间线段最短.
18.解:汽车的雨刷实际上是一条线,通过运动把玻璃上的雨水刷干净,所以应是线动成面.
故答案为:线动成面.
19.解:S阴影=S圆形﹣S正方形=π×()2﹣×2×2=π﹣2≈1.14(cm2),
故答案为:1.14.
20.解:∵正方体的表面展开图,相对的面之间一定相隔一个正方形,
∴“守”字一面的相对面上的字是“善”.
故答案为:善.
三.解答题
21.解:(1)由题意得,2×(12×6+12×6+6×6)=360cm2;
答:制作这样的包装盒需要360平方厘米的硬纸板;
(2)360÷10000×5×10=1.8元,
答:制作10个这的包装盒需花费1.8元钱.
22.解:设倒完以后,第一个容器中的水面离容器口有x
cm,
则:π×42×(20﹣x)=π×62×8,
解得:x=2,
答:第一个容器中的水面离容器口有2
cm.
23.解:以8cm为轴,得
以8cm为轴体积为×π×62×8=96π(cm3),
以6cm为轴,得
以6cm为轴的体积为×π×82×6=128π(cm3),
以10cm为轴,得
以10cm为轴的体积为×π()2×10=76.8π(cm3).
故几何体的体积为:96πcm3或128πcm3或76.8πcm3.
24.解:①∵点O是线段AB的中点,OB=14cm,
∴AB=2OB=28cm,
∵AP:PB=5:2.
∴BP=cm,
∴OP=OB﹣BP=14﹣8=6(cm);
②如图1,当M点在P点的左边时,
AM=AB﹣(PM+BP)=28﹣(4+8)=16(cm),
如图2,当M点在P点的右边时,
AM=AB﹣BM=AB﹣(BP﹣PM)=28﹣(8﹣4)=24(cm).
综上,AM=16cm或24cm.
25.解:(1)由题可得,截面的形状为长方形;
(2)∵△ADE是周长为3的等边三角形,
∴DE=AD=1,
又∵△ABC是周长为10的等边三角形,
∴AB=AC=BC=,
∴DB=EC=﹣1=,
∴四边形DECB的周长=1+×2+=9.
26.解:丁说的对.
(1)当四点共线时,可画1条,如图(1);
(2)当四点中有三点共线时,可画4条,如图(2);
(3)当四点中任意三点不共线时,可画6条,如图(3);
27.解:∵AC=18cm,CB=AC,
∴BC=×18=12cm,
则AB=AC+BC=30cm,
∵D、E分别为AC、AB的中点,
∴AD=AC=9cm,AE=AB=15cm,
∴DE=AE﹣AD=15﹣9=6cm,
答:DE的长是6cm.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
