10.1分式的概念-沪教版(上海)七年级数学上册课件(25张)
文档属性
| 名称 | 10.1分式的概念-沪教版(上海)七年级数学上册课件(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 09:28:36 | ||
图片预览







文档简介
(共25张PPT)
10.1分式的概念
能用分式表示现实情境中的数量关系,
体会分式的模型思想,进一步发展符号感。
求一个分式有意义的条件。
难点:
重点:
了解分式的形式,并理解分式概念中的一个特点:分母中含有字母;一个要求:字母的取值限制于使分母的值不得为0。
了解分式的概念,明确分式与整式的区别。
学习目标
(1)面积为2平方米的长方形一边长3米,则它的另一边长为________米;
(2)面积为s平方米的长方形一边长a米,则它的另一边长为________米;
(3)一箱苹果售价p元,总重m千克,箱重n千克.则每千克苹果的售价是_______元.
两个整数相除,不能整除时结果可用分数表示.当两个整式不能整除时,它们的商应该怎么表示呢?
2
3
a
s
m-n
p
做一做
大家谈谈
分母中含有字母.
上面的问题出现了代数式
这些代数式与整式有什么不同?这些代数式有什么共同特征?
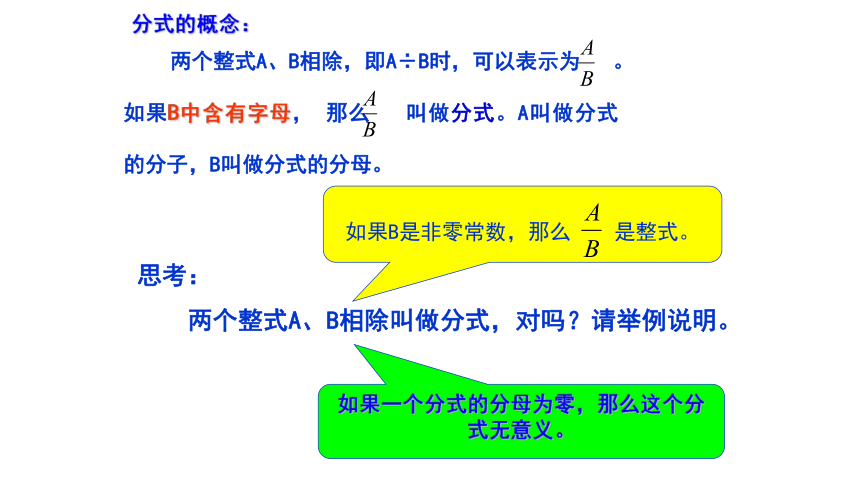
两个整式A、B相除,即A÷B时,可以表示为
。如果B中含有字母,
那么
叫做分式。A叫做分式的分子,B叫做分式的分母。
分式的概念:
思考:
两个整式A、B相除叫做分式,对吗?请举例说明。
如果B是非零常数,那么
是整式。
如果一个分式的分母为零,那么这个分式无意义。
探究
x
-2
-1
0
1
2
请你填表:
1
x
思考:X取任意值时,分式都有具体结果吗?
1
2
-1
1
1
2
1
3
-1
3
无意义
0
无意义
分式中字母的取值不能使使
.
分母为零.
当分母的值
为零时,分式就没有意义.
当
例1、下列各有理式中,哪些是整式?哪些是分式?
为什么(2)、(4)不是分式?判断的关键是什么?
解:属于整式的有(2)、(4)
属于分式的有(1)、(3)
分母含有字母是分式,
分母不含字母是整式.
1.下列代数式哪些是整式?
复习引入
活动1
,
,
,
,
,
,
,
.
,
,
.
整式是:
,
.
,
,
,
;
,
,
,
,
,
.
2.余下的代数式为何不是整式?有何特征?
分母中均含有字母
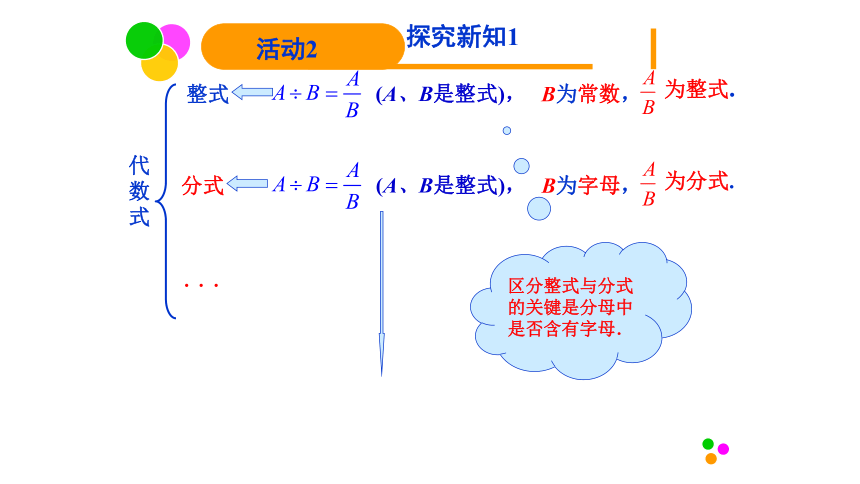
(A、B是整式),
为整式.
当B为常数时,
(A、B是整式),
为分式.
当B为字母时,
探究新知1
活动2
区分整式与分式的关键是分母中是否含有字母.
代
数
式
整式
分式
·
·
·
(A、B是整式),
为整式.
B为常数,
(A、B是整式),
为分式.
B为字母,
探究新知2
活动3
.
问:当
x=1
时,能求出此分式的值吗?
解:当x=-1时,
求代数式的值:
1.代入;
2.计算.
分式
中分母B=0
分式
无意义
例题1
当x=-1时,求分式
的值.
例、当x取什么值时,下列分式无意义?
变式训练:
(1)当x取什么值时,分式
有意义。
(2)当x取什么值时,分式
有意义。
例题分析:
如果分母为零,那么分式无意义。
如果分母不为零,那么分式有意义。
(2)如果x+2=0,那么x=-2,所以,当x=-2时,此分式无意义。
探究新知2
活动3
要使分式无意义,只要将分母的值取为零.
例题2
当x取何值时,下列分式无意义?
(1)
;
(2)
.
解:(1)当分母2x=0,即x=0时,此分式无意义.
(2)当分母x+2=0,即x=-2时,此分式无意义.
探究新知2
活动3
变式:
当x取何值时,下列分式有意义?
(1)
;
(2)
.
分式
中分母B≠0
分式
有意义
分析:
解:(1)当2x≠0,即x
≠
0时,分式
有意义.
(2)当x+2≠0,即x
≠
-2时,分式
有意义.
分式
B=0
分式
无意义
B≠0
分式
有意义
课堂练习
活动4
.
【试一试】
(1)当x取什么值时,分式
无意义.
有意义.
(2)当x取什么值时,分式
解:(1)当
,即
时,分式
无意义.
(2)当
,即
时,分式
有意义.
【议一议】
当m取什么值时,分式
有意义.
分析:∵
∴
∴
m取任意数值时,分式恒有意义.
例、当y是什么值时,分式
的值是0?
分析:分式的值为0需满足的条件是分子的值为0且分母的值不为0。
例题分析:
变式训练:
(1)当y是什么值时,分式
的值是0?
(2)当y是什么值时,分式
的值是正数?
探究新知3
活动5
.
例题3
当x取何值时,分式
的值为零?
分析:分式
,当A=0,且B≠0
分式值为零.
解:由题意得:分子2x+1=0,
得
,
∴当x=
时,分式
的值为零.
当
时,
分母3x-1
≠0.
探究新知3
活动5
.
【做一做】
当y取何值时,分式
的值为零?
解:由题意,得分子y-4=0,
当y=4时,分母2y+3≠0
分式值为零的条件:
1.分式的分子为零;
2.保证分母的值不为零.
y=4,
的值为零.
∴当y=4时,分式
注意:
在分式中,分母的值不能是零。如果分母的值是零,则分式没有意义。
a
s
m-n
9
例如:在分式
中,a≠0;
在分式
中,m
-
n
≠
0,即m≠n.
阅读下面一题的解答过程,试判断是否正确,如果不正确,请加以改正。
当x是什么数时,分式 的值是零?
解:由分子
|x|
-4=0,得x=±4
所以当x=±4时,分式
的值是零.
用心填一填
(1)当__________时,分式
有意义;
(2)当___________时,分式
无意义;
(3)当___________时,分式
的值为零;
(4)当______________时,分式
的值为零;
(5)当________________
时,分式
有意义;
x≠0
x=2
x=3
x≠-1且x≠
2
x=
-1
当
_____________
时,分式
x=-1或x=
2
无意义;
选择:
1.使分式
有意义的
值必为
(
)
A
B
C
D
任意有理数
B
分析:
分母
得
2.当
时,分式①
②
③
④
无意义的是
A
①②
B
②③
C
①③
D
②④
(
)
C
判断:
1、对于任意有理数
,分式
有意义
(
)
2、若分式
无意义,则
的值一定是-3
(
)
√
×
则
无论
取何值,
分析
拓展提高
活动6
1.当x取何值时,分式
值为零?
当x=1时,分母1-x=0,
∴x=1舍去.
∴当x=-1时,分式
的值为零.
解:由题意得分子
,
当x=-1时,分母1-x
≠0.
分式值为零的条件:
1.分式的分子为零;
2.保证分母的值不为零.
拓展提高
活动6
2.对于分式
.
(1)使分式无意义的x,y有多少对?
(2)使分式有意义的x,y有多少对?x,y应有什么关系?
(3)如果x=1,那么y取何值时,分式无意义?
(4)如果当y=1,那么x取何值时,分式有意义?
(5)如果x=-1,那么y取什么值时,分式的值为零?
解:(1)无数对;
(2)无数对,
(3)
;
(4)
;
(5)
由-1-y=0得y=-1,此时-1+2y≠0,故y=-1时分式值为零.
谈一谈这一节课你的收获和体会
。
归纳小结
①分子分母都是整式
②分母中必含有字母
分母中字母的取值不能使分母值为零,否则分式无意义.
当分子为零且分母不为零时,分式值为零.
分式的概念
10.1分式的概念
能用分式表示现实情境中的数量关系,
体会分式的模型思想,进一步发展符号感。
求一个分式有意义的条件。
难点:
重点:
了解分式的形式,并理解分式概念中的一个特点:分母中含有字母;一个要求:字母的取值限制于使分母的值不得为0。
了解分式的概念,明确分式与整式的区别。
学习目标
(1)面积为2平方米的长方形一边长3米,则它的另一边长为________米;
(2)面积为s平方米的长方形一边长a米,则它的另一边长为________米;
(3)一箱苹果售价p元,总重m千克,箱重n千克.则每千克苹果的售价是_______元.
两个整数相除,不能整除时结果可用分数表示.当两个整式不能整除时,它们的商应该怎么表示呢?
2
3
a
s
m-n
p
做一做
大家谈谈
分母中含有字母.
上面的问题出现了代数式
这些代数式与整式有什么不同?这些代数式有什么共同特征?
两个整式A、B相除,即A÷B时,可以表示为
。如果B中含有字母,
那么
叫做分式。A叫做分式的分子,B叫做分式的分母。
分式的概念:
思考:
两个整式A、B相除叫做分式,对吗?请举例说明。
如果B是非零常数,那么
是整式。
如果一个分式的分母为零,那么这个分式无意义。
探究
x
-2
-1
0
1
2
请你填表:
1
x
思考:X取任意值时,分式都有具体结果吗?
1
2
-1
1
1
2
1
3
-1
3
无意义
0
无意义
分式中字母的取值不能使使
.
分母为零.
当分母的值
为零时,分式就没有意义.
当
例1、下列各有理式中,哪些是整式?哪些是分式?
为什么(2)、(4)不是分式?判断的关键是什么?
解:属于整式的有(2)、(4)
属于分式的有(1)、(3)
分母含有字母是分式,
分母不含字母是整式.
1.下列代数式哪些是整式?
复习引入
活动1
,
,
,
,
,
,
,
.
,
,
.
整式是:
,
.
,
,
,
;
,
,
,
,
,
.
2.余下的代数式为何不是整式?有何特征?
分母中均含有字母
(A、B是整式),
为整式.
当B为常数时,
(A、B是整式),
为分式.
当B为字母时,
探究新知1
活动2
区分整式与分式的关键是分母中是否含有字母.
代
数
式
整式
分式
·
·
·
(A、B是整式),
为整式.
B为常数,
(A、B是整式),
为分式.
B为字母,
探究新知2
活动3
.
问:当
x=1
时,能求出此分式的值吗?
解:当x=-1时,
求代数式的值:
1.代入;
2.计算.
分式
中分母B=0
分式
无意义
例题1
当x=-1时,求分式
的值.
例、当x取什么值时,下列分式无意义?
变式训练:
(1)当x取什么值时,分式
有意义。
(2)当x取什么值时,分式
有意义。
例题分析:
如果分母为零,那么分式无意义。
如果分母不为零,那么分式有意义。
(2)如果x+2=0,那么x=-2,所以,当x=-2时,此分式无意义。
探究新知2
活动3
要使分式无意义,只要将分母的值取为零.
例题2
当x取何值时,下列分式无意义?
(1)
;
(2)
.
解:(1)当分母2x=0,即x=0时,此分式无意义.
(2)当分母x+2=0,即x=-2时,此分式无意义.
探究新知2
活动3
变式:
当x取何值时,下列分式有意义?
(1)
;
(2)
.
分式
中分母B≠0
分式
有意义
分析:
解:(1)当2x≠0,即x
≠
0时,分式
有意义.
(2)当x+2≠0,即x
≠
-2时,分式
有意义.
分式
B=0
分式
无意义
B≠0
分式
有意义
课堂练习
活动4
.
【试一试】
(1)当x取什么值时,分式
无意义.
有意义.
(2)当x取什么值时,分式
解:(1)当
,即
时,分式
无意义.
(2)当
,即
时,分式
有意义.
【议一议】
当m取什么值时,分式
有意义.
分析:∵
∴
∴
m取任意数值时,分式恒有意义.
例、当y是什么值时,分式
的值是0?
分析:分式的值为0需满足的条件是分子的值为0且分母的值不为0。
例题分析:
变式训练:
(1)当y是什么值时,分式
的值是0?
(2)当y是什么值时,分式
的值是正数?
探究新知3
活动5
.
例题3
当x取何值时,分式
的值为零?
分析:分式
,当A=0,且B≠0
分式值为零.
解:由题意得:分子2x+1=0,
得
,
∴当x=
时,分式
的值为零.
当
时,
分母3x-1
≠0.
探究新知3
活动5
.
【做一做】
当y取何值时,分式
的值为零?
解:由题意,得分子y-4=0,
当y=4时,分母2y+3≠0
分式值为零的条件:
1.分式的分子为零;
2.保证分母的值不为零.
y=4,
的值为零.
∴当y=4时,分式
注意:
在分式中,分母的值不能是零。如果分母的值是零,则分式没有意义。
a
s
m-n
9
例如:在分式
中,a≠0;
在分式
中,m
-
n
≠
0,即m≠n.
阅读下面一题的解答过程,试判断是否正确,如果不正确,请加以改正。
当x是什么数时,分式 的值是零?
解:由分子
|x|
-4=0,得x=±4
所以当x=±4时,分式
的值是零.
用心填一填
(1)当__________时,分式
有意义;
(2)当___________时,分式
无意义;
(3)当___________时,分式
的值为零;
(4)当______________时,分式
的值为零;
(5)当________________
时,分式
有意义;
x≠0
x=2
x=3
x≠-1且x≠
2
x=
-1
当
_____________
时,分式
x=-1或x=
2
无意义;
选择:
1.使分式
有意义的
值必为
(
)
A
B
C
D
任意有理数
B
分析:
分母
得
2.当
时,分式①
②
③
④
无意义的是
A
①②
B
②③
C
①③
D
②④
(
)
C
判断:
1、对于任意有理数
,分式
有意义
(
)
2、若分式
无意义,则
的值一定是-3
(
)
√
×
则
无论
取何值,
分析
拓展提高
活动6
1.当x取何值时,分式
值为零?
当x=1时,分母1-x=0,
∴x=1舍去.
∴当x=-1时,分式
的值为零.
解:由题意得分子
,
当x=-1时,分母1-x
≠0.
分式值为零的条件:
1.分式的分子为零;
2.保证分母的值不为零.
拓展提高
活动6
2.对于分式
.
(1)使分式无意义的x,y有多少对?
(2)使分式有意义的x,y有多少对?x,y应有什么关系?
(3)如果x=1,那么y取何值时,分式无意义?
(4)如果当y=1,那么x取何值时,分式有意义?
(5)如果x=-1,那么y取什么值时,分式的值为零?
解:(1)无数对;
(2)无数对,
(3)
;
(4)
;
(5)
由-1-y=0得y=-1,此时-1+2y≠0,故y=-1时分式值为零.
谈一谈这一节课你的收获和体会
。
归纳小结
①分子分母都是整式
②分母中必含有字母
分母中字母的取值不能使分母值为零,否则分式无意义.
当分子为零且分母不为零时,分式值为零.
分式的概念
