10.2分式的基本性质-沪教版(上海)七年级数学上册课件(共21张ppt)
文档属性
| 名称 | 10.2分式的基本性质-沪教版(上海)七年级数学上册课件(共21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 585.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 07:47:26 | ||
图片预览








文档简介
(共21张PPT)
10.2分式的基本性质
当x取什么值时,下列分式有意义?
复习:
分式的分子与分母都乘以(或除)同一个不等于0的整式,分式的值不变.
为什么所乘的整式不能为0呢?
分式的基本性质:
合作交流
一.分式的基本性质
(一)下列等式的右边是怎样从左边得到的?
(二)填空:①
②
想一想:(2)中为什么不给出x
≠0,而(2)中却给出了c
≠0?
下列各组分式,能否由左边变形为右边?
与
判
断
反思:运用分式的基本性质应注意什么?
(1)”都”
(2)”同一个”
(3)”不为0”
(2)
与
(3)
与
(4)
与
下列分式的右边是怎样从左边得到的?
⑴
;
⑵
例
反思:为什么(1)中有附加条件y≠0,
而(2)中没有附加条件x≠0?
b
a
bx
ax
=
把分式分子、分母的公因式约去,这种变形叫分式的约分.
分式的基本性质
分式约分的依据是什么?
分式的约分
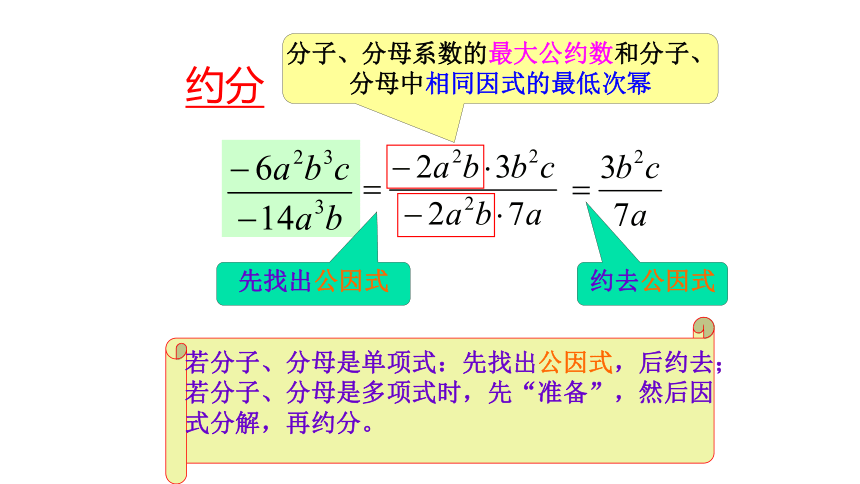
约分的基本步骤:
(1)若分子﹑分母都是单项式,则约去系数的最大公约数,并约去分子、分母相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母所有的公因式.
约分
若分子、分母是单项式:先找出公因式,后约去;若分子、分母是多项式时,先“准备”,然后因式分解,再约分。
先找出公因式
约去公因式
分子、分母系数的最大公约数和分子、分母中相同因式的最低次幂
例题
(1)
(2)
约去系数的最大公约数,和分子分母相同字母的最低次幂
先把分子、分母分别分解因式,然后约去公因式.
约分:
分子与分母没有公因式的分式称为最简分式.
议一议
(1)求分式
的最简公分母。
分析:
对于三个分式的分母中的系数2,4,6,取其最小公倍数12;对于三个分式的分母的字母,字母x为底的幂的因式,取其最高次幂x?,字母y为底的幂的因式,取其最高次幂y4,再取字母z.所以三个分式的公分母为12x?y4z.
(2)求分式
与
的最简公分母.
=-2x(x-2)
把这两个分式的分母中所有的因式都取到,
其中,系数取正数,取它们的积,
即
就是这两个分式的最简公分母.
2x(x+2)
(x-2)
4x-2x?
=
2x(2
-x)
x?-4
=
(x+2)(x
-2)
x?-4
1
4x-2x?
1
的最简公分母是________________.
(3)分式
a?-4a
+4=
(a
-2)?
4a?-8a
+4=
4(a
-1)?
3a
-
6=
3(a
-2)
12(a
-2)?
(a
-1)?
填空,使等式成立.
⑴
(其中
x+y
≠0
)
⑵
想一想
反思:你是怎么想的?
1、把下面的分数通分:
2、什么叫分数的通分?
答:把几个异分母的分数化成同分母的分数,而不改变分数的值,叫做分数的通分。
3、和分数通分类似,把几个异分母的分式化成与原来的分式相等的同分母的分式叫做分式的通分。
4、通分的关键是确定几个分式的公分母。
,
,
例
通分:
(1)
;
(2)
,
(3)
;
.
例题讲解与练习
公分母如何确定呢?
最简公分母
若分母是多项式时,应先将各分母分解因式,再找出最简公分母。
1、各分母系数的最小公倍数。
2、各分母所含有的因式。
3、各分母所含相同因式的最高次幂。
4、所得的系数与各字母(或因式)的最高次幂的积(其中系数都取正数)
通分:
例
通分的关键是确定几个分式的公分母,通常取各分母所有因式的最高次幂的积作为公分母.
(3)
x?+xy
1
x?-y?
1
,
∵
x?-y?=____________,
x?
+xy=__________,
∴
与
的最简公分母为____________,
因此
x?+xy
1
x?-y?
1
=________________,
=________________,
x?+xy
1
x?-y?
1
(x+y)(x-y)
x(x+y)
x(x+y)(x-y)
x(x+y)(x-y)
x
x(x+y)(x-y)
x-y
x?-xy?
x
x?-xy?
x
-y
先把分母分解因式
二.分式中的符号法则
分式的分子、分母与分式本身的符号,同时改变两处的符号,分式的值不变.
例1.不改变分式的值,使下列分式的分子与分母都不含”一”号
练习:不改变分式的值,使下列分式的分子与分母都不含”一”号
B
A
3.下列各式成立的是(
)
D
A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍
1.若把分式
的
x
和
y
都扩大两倍,则分式的值(
)
y
x+y
2.若把分式
中的x
和y都扩大3倍,那么分式的值(
).
A.扩大3倍 B.扩大9倍
C.扩大4倍
D.不变
xy
x+y
A.
c
b-a
c
a+b
=
B.
c
a-b
c
b-a
=
C.
c
b-a
-c
a+b
=
D.
c
b-a
c
a-b
=-
你认为小红的解答对吗?如果不正确,请说明理由,
并给出正确的解答。
字母的取值,分式是否有意义。
4、有一道题目:当x=4时,求分式
的值。小红是这样解的:
x3-16x
2x-8
x(x-4)(x+4)
2(x-4)
=
x2+4x
2
解:原式=
=
当x=4时,原式=
42+4×4
2
16
1
课堂小结
1.分式的基本性质是什么?
2.符号法则
3.分式的约分与最简分式.
10.2分式的基本性质
当x取什么值时,下列分式有意义?
复习:
分式的分子与分母都乘以(或除)同一个不等于0的整式,分式的值不变.
为什么所乘的整式不能为0呢?
分式的基本性质:
合作交流
一.分式的基本性质
(一)下列等式的右边是怎样从左边得到的?
(二)填空:①
②
想一想:(2)中为什么不给出x
≠0,而(2)中却给出了c
≠0?
下列各组分式,能否由左边变形为右边?
与
判
断
反思:运用分式的基本性质应注意什么?
(1)”都”
(2)”同一个”
(3)”不为0”
(2)
与
(3)
与
(4)
与
下列分式的右边是怎样从左边得到的?
⑴
;
⑵
例
反思:为什么(1)中有附加条件y≠0,
而(2)中没有附加条件x≠0?
b
a
bx
ax
=
把分式分子、分母的公因式约去,这种变形叫分式的约分.
分式的基本性质
分式约分的依据是什么?
分式的约分
约分的基本步骤:
(1)若分子﹑分母都是单项式,则约去系数的最大公约数,并约去分子、分母相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母所有的公因式.
约分
若分子、分母是单项式:先找出公因式,后约去;若分子、分母是多项式时,先“准备”,然后因式分解,再约分。
先找出公因式
约去公因式
分子、分母系数的最大公约数和分子、分母中相同因式的最低次幂
例题
(1)
(2)
约去系数的最大公约数,和分子分母相同字母的最低次幂
先把分子、分母分别分解因式,然后约去公因式.
约分:
分子与分母没有公因式的分式称为最简分式.
议一议
(1)求分式
的最简公分母。
分析:
对于三个分式的分母中的系数2,4,6,取其最小公倍数12;对于三个分式的分母的字母,字母x为底的幂的因式,取其最高次幂x?,字母y为底的幂的因式,取其最高次幂y4,再取字母z.所以三个分式的公分母为12x?y4z.
(2)求分式
与
的最简公分母.
=-2x(x-2)
把这两个分式的分母中所有的因式都取到,
其中,系数取正数,取它们的积,
即
就是这两个分式的最简公分母.
2x(x+2)
(x-2)
4x-2x?
=
2x(2
-x)
x?-4
=
(x+2)(x
-2)
x?-4
1
4x-2x?
1
的最简公分母是________________.
(3)分式
a?-4a
+4=
(a
-2)?
4a?-8a
+4=
4(a
-1)?
3a
-
6=
3(a
-2)
12(a
-2)?
(a
-1)?
填空,使等式成立.
⑴
(其中
x+y
≠0
)
⑵
想一想
反思:你是怎么想的?
1、把下面的分数通分:
2、什么叫分数的通分?
答:把几个异分母的分数化成同分母的分数,而不改变分数的值,叫做分数的通分。
3、和分数通分类似,把几个异分母的分式化成与原来的分式相等的同分母的分式叫做分式的通分。
4、通分的关键是确定几个分式的公分母。
,
,
例
通分:
(1)
;
(2)
,
(3)
;
.
例题讲解与练习
公分母如何确定呢?
最简公分母
若分母是多项式时,应先将各分母分解因式,再找出最简公分母。
1、各分母系数的最小公倍数。
2、各分母所含有的因式。
3、各分母所含相同因式的最高次幂。
4、所得的系数与各字母(或因式)的最高次幂的积(其中系数都取正数)
通分:
例
通分的关键是确定几个分式的公分母,通常取各分母所有因式的最高次幂的积作为公分母.
(3)
x?+xy
1
x?-y?
1
,
∵
x?-y?=____________,
x?
+xy=__________,
∴
与
的最简公分母为____________,
因此
x?+xy
1
x?-y?
1
=________________,
=________________,
x?+xy
1
x?-y?
1
(x+y)(x-y)
x(x+y)
x(x+y)(x-y)
x(x+y)(x-y)
x
x(x+y)(x-y)
x-y
x?-xy?
x
x?-xy?
x
-y
先把分母分解因式
二.分式中的符号法则
分式的分子、分母与分式本身的符号,同时改变两处的符号,分式的值不变.
例1.不改变分式的值,使下列分式的分子与分母都不含”一”号
练习:不改变分式的值,使下列分式的分子与分母都不含”一”号
B
A
3.下列各式成立的是(
)
D
A.扩大两倍 B.不变
C.缩小两倍 D.缩小四倍
1.若把分式
的
x
和
y
都扩大两倍,则分式的值(
)
y
x+y
2.若把分式
中的x
和y都扩大3倍,那么分式的值(
).
A.扩大3倍 B.扩大9倍
C.扩大4倍
D.不变
xy
x+y
A.
c
b-a
c
a+b
=
B.
c
a-b
c
b-a
=
C.
c
b-a
-c
a+b
=
D.
c
b-a
c
a-b
=-
你认为小红的解答对吗?如果不正确,请说明理由,
并给出正确的解答。
字母的取值,分式是否有意义。
4、有一道题目:当x=4时,求分式
的值。小红是这样解的:
x3-16x
2x-8
x(x-4)(x+4)
2(x-4)
=
x2+4x
2
解:原式=
=
当x=4时,原式=
42+4×4
2
16
1
课堂小结
1.分式的基本性质是什么?
2.符号法则
3.分式的约分与最简分式.
