人教版数学八年级上册14.2.2完全平方公式-添括号法则 课件(17张)
文档属性
| 名称 | 人教版数学八年级上册14.2.2完全平方公式-添括号法则 课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
添括号法则
1.去括号的法则是什么?
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不改变正负号。
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号。
2.去括号:
解:
上面是根据去括号法则,由左边式子得右边式子,现在我们把上面四个式子反过来
(1)
a+b-c=a+(b-c)
(2)
a-b-c=a+(-b-c)
(3)
a+b-c=a-(-b+c)
(4)
a-b+c=a-(b-c)
3
a
+
b
–
c
=
a
+
(
b
–
c)
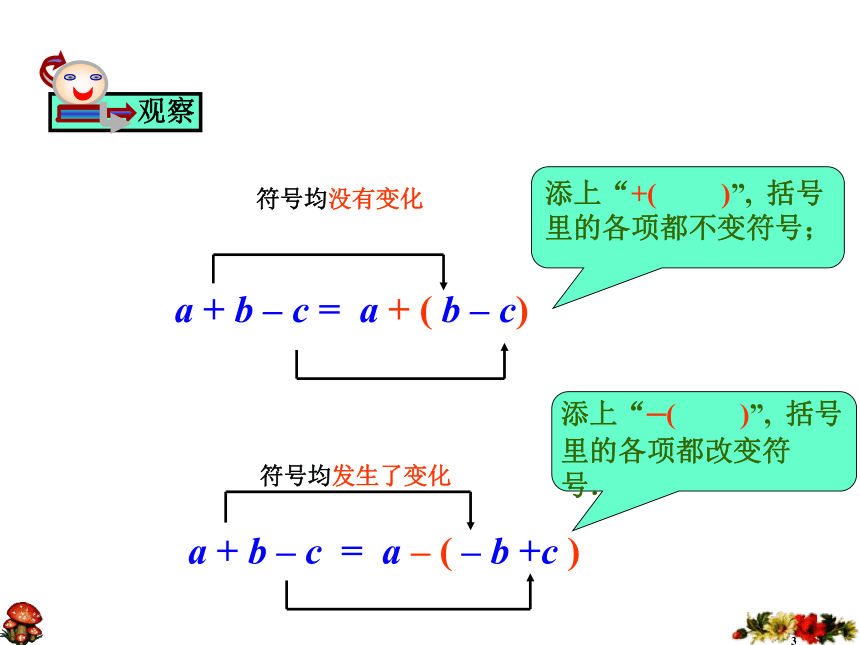
符号均没有变化
a
+
b
–
c
=
a
–
(
–
b
+c
)
符号均发生了变化
添上“+(
)”,
括号里的各项都不变符号;
添上“–(
)”,
括号里的各项都改变符号.
观察
添括号法则
添括号时,
如果括号前面是正号,括到括号里的各项都不变符号;
如果括号前面是负号,括到括号里的各项都改变符号.
遇“加”不变,遇“减”都变.
1、下列各式,等号右边添的括号正确吗?
若不正确,可怎样改正?
各显身手
检验方法:
用去括号法则
来检验添括号是否正确
2、做一做:
.在括号内填入适当的项:
(1)
x
?–x+1
=
x
?
–(
);
(2)
2
x
?–3
x–1=
2
x
?
+(
);
(3)(a–b)–(c–d)=
a
–(
).
x–1
–3x–1
b
+
c
–
d
运用乘法公式计算:
(1)
(
x
+2y-3)
(x-
2y
+3)
;
(2)
(a
+
b
+c
)
2.
解:
(1)
(
x
+2y-3)
(x-
2y
+3)
=
[
x+
(2y
–
3
)]
[
x-
(2y-3)
]
=
x2-
(2y-
3)2
=
x2-
(
4y2-12y+9)
=
x2-4y2+12y-9.
(a
+
b
+c
)
2
=
[
(a+b)
+c
]2
=
(a+b)2
+2
(a+b)c
+c2
=
a2+2ab
+b2
+2ac
+2bc
+c2
=
a2+b2+c2
+2ab+2bc
+2ac.
3.
填空:
2xy?
–
x?
–
y?
+
3x?y
=+(
)
=
–(
)
=
2xy?
–
(
)+
3x?y
=
2xy?
+
(
)+
3x?y
=
2xy?
–
(
)
–
x?
2xy?
–
x?
–
y?
+
3x?y
–
2xy?
+
x?
+
y?
–
3x?y
x?
+
y?
–
x?
–
y?
y?
–
3x?y
(1)
3x?
y?
–
2
x?
+
y?
(2)
–
a?
+
2a?
–
a
+1
(3)
3x?
–
2xy?
+
2y?
4.
给下列多项式添括号,使它们的最高次项系数为正数.
如:
–
x?
+
x
=
–(x?
–
x);
x?
–
x
=
+
(x?
–
x)
练一练
=
+(
)
=
–(
)
=
–(
)
=
–(
)
9
3x?
y?
–
2
x?
+
y?
a?
–
2a?
+
a
–
1
–
3x?
+
2xy?
–
2y?
2xy?–
3x?
–
2y?
化简求值:2x?y
–3xy?
+
4x?y–5
xy?
其中x=1,y=-1.
解:
2x?y
–3xy?
+
4x?y–5
xy?
=(2x?y
+
4x?y)
–(3xy?
+
5
xy?)
=6x?y–8xy?
当x=1,y=-1时
原式=6×1?×(–1)–8×1×(
–1
)?
=
–6–8
=
–14
用简便方法计算:
(1)214a+47a+53a;(2)214a
–
39a
–
61a.
7
解:
(1)
214a+47a+53a
=
214a+(47a+53a)
=
214a+100a
=
314a
(2)
214a
–
39a
–
61a
=214a
–
(39a
+
61a)
=214a
–
100a
=114a
1.??用简便方法计算:
(1)
117x
+
138x
–
38x
;
(2)
125x
–
64x
–
36x
;
????(3)
136x
–
87x
+
57x
.
当
时,
求
的值。
添括号法则
1.去括号的法则是什么?
括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不改变正负号。
括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号。
2.去括号:
解:
上面是根据去括号法则,由左边式子得右边式子,现在我们把上面四个式子反过来
(1)
a+b-c=a+(b-c)
(2)
a-b-c=a+(-b-c)
(3)
a+b-c=a-(-b+c)
(4)
a-b+c=a-(b-c)
3
a
+
b
–
c
=
a
+
(
b
–
c)
符号均没有变化
a
+
b
–
c
=
a
–
(
–
b
+c
)
符号均发生了变化
添上“+(
)”,
括号里的各项都不变符号;
添上“–(
)”,
括号里的各项都改变符号.
观察
添括号法则
添括号时,
如果括号前面是正号,括到括号里的各项都不变符号;
如果括号前面是负号,括到括号里的各项都改变符号.
遇“加”不变,遇“减”都变.
1、下列各式,等号右边添的括号正确吗?
若不正确,可怎样改正?
各显身手
检验方法:
用去括号法则
来检验添括号是否正确
2、做一做:
.在括号内填入适当的项:
(1)
x
?–x+1
=
x
?
–(
);
(2)
2
x
?–3
x–1=
2
x
?
+(
);
(3)(a–b)–(c–d)=
a
–(
).
x–1
–3x–1
b
+
c
–
d
运用乘法公式计算:
(1)
(
x
+2y-3)
(x-
2y
+3)
;
(2)
(a
+
b
+c
)
2.
解:
(1)
(
x
+2y-3)
(x-
2y
+3)
=
[
x+
(2y
–
3
)]
[
x-
(2y-3)
]
=
x2-
(2y-
3)2
=
x2-
(
4y2-12y+9)
=
x2-4y2+12y-9.
(a
+
b
+c
)
2
=
[
(a+b)
+c
]2
=
(a+b)2
+2
(a+b)c
+c2
=
a2+2ab
+b2
+2ac
+2bc
+c2
=
a2+b2+c2
+2ab+2bc
+2ac.
3.
填空:
2xy?
–
x?
–
y?
+
3x?y
=+(
)
=
–(
)
=
2xy?
–
(
)+
3x?y
=
2xy?
+
(
)+
3x?y
=
2xy?
–
(
)
–
x?
2xy?
–
x?
–
y?
+
3x?y
–
2xy?
+
x?
+
y?
–
3x?y
x?
+
y?
–
x?
–
y?
y?
–
3x?y
(1)
3x?
y?
–
2
x?
+
y?
(2)
–
a?
+
2a?
–
a
+1
(3)
3x?
–
2xy?
+
2y?
4.
给下列多项式添括号,使它们的最高次项系数为正数.
如:
–
x?
+
x
=
–(x?
–
x);
x?
–
x
=
+
(x?
–
x)
练一练
=
+(
)
=
–(
)
=
–(
)
=
–(
)
9
3x?
y?
–
2
x?
+
y?
a?
–
2a?
+
a
–
1
–
3x?
+
2xy?
–
2y?
2xy?–
3x?
–
2y?
化简求值:2x?y
–3xy?
+
4x?y–5
xy?
其中x=1,y=-1.
解:
2x?y
–3xy?
+
4x?y–5
xy?
=(2x?y
+
4x?y)
–(3xy?
+
5
xy?)
=6x?y–8xy?
当x=1,y=-1时
原式=6×1?×(–1)–8×1×(
–1
)?
=
–6–8
=
–14
用简便方法计算:
(1)214a+47a+53a;(2)214a
–
39a
–
61a.
7
解:
(1)
214a+47a+53a
=
214a+(47a+53a)
=
214a+100a
=
314a
(2)
214a
–
39a
–
61a
=214a
–
(39a
+
61a)
=214a
–
100a
=114a
1.??用简便方法计算:
(1)
117x
+
138x
–
38x
;
(2)
125x
–
64x
–
36x
;
????(3)
136x
–
87x
+
57x
.
当
时,
求
的值。
