_北师大版(2012)数学九年级上册4.4相似三角形的判定
文档属性
| 名称 | _北师大版(2012)数学九年级上册4.4相似三角形的判定 |

|
|
| 格式 | zip | ||
| 文件大小 | 269.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 00:00:00 | ||
图片预览



文档简介
相似三角形的判定(第1课时)
一、教学目标
1.
通过一些具体情境,深化对相似三角形的认识和理解;
2.
掌握并理解平行线分线段成比例定理;
3.
掌握平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似和相似三角形的判定方法,并能运用这个定理进行相似三角形的判定.
二、重点:运用相似三角形的基本定理和判定方法进行证明.
难点:
对“平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似”这一定理的两种情形的理解与掌握.
三、学情分析
相似三角形的判定既是本章的重点,也是整个初中几何的重点。同时,在我们的生活中相似图形的应用也比较广泛。由于有了相似图形、相似多边形和全等三角形的基础,学生应不难理解。
四、自主探究
问题一:相似三角形的概念及表示
1、
什么叫相似三角形?
2、怎样表示两三角形相似?
3、什么是三角形的相似比?
4、如果相似比k=1,两三角形有怎样的关系?
问题二:平行线分线段成比例定理
1、已知如图,直线,直线分别交于点A、B、C、D、E、F.
(1)分别测量线段AB、BC、DE、EF的长度;
(2)计算,的值,你有什么发现?
(3)任意移动,再测量DE、EF的长度,并计算的值,你又有什么发现?
(4)任意平移,再测量AB、BC、DE、EF的长度,计算,的值,上述规律还成立吗?
(5)验证,成立吗?
(6)由上述探究,你能发现什么规律?
2、(1)若1中的相交于上点A,如图,你会得到什么结论?
(2)若1中的相交于上点A,如图,你会得到什么结论?
(3)把(1)中的看成平行于△ABC的边BC的直线,把(2)中的看成平行于△ABC的边BC的直线,你会得到什么结论?
问题三:相似三角形的预备定理
1、在△ABC中,DE∥BC,分别交AB,AC于点D,E,△ADE与△ABC有什么关系?
2、由上题,请你归纳结论.
3、【引申】上述结论中,如果平行线与其他两边延长线相交结论仍成立,你能画出正确的图形吗?
二、尝试应用
1.如图,已知,那么下列结论正确的是(
)
A.
B.
C.
D.
2、如图,在平行四边形ABCD中,E是AD上一点,连结CE并延长交BA的延长线于点F,则下列结论中错误的是
(
)
A.∠AEF=∠DEC
B.FA:CD=AE:BC
C.FA:AB=FE:EC
D.AB=DC
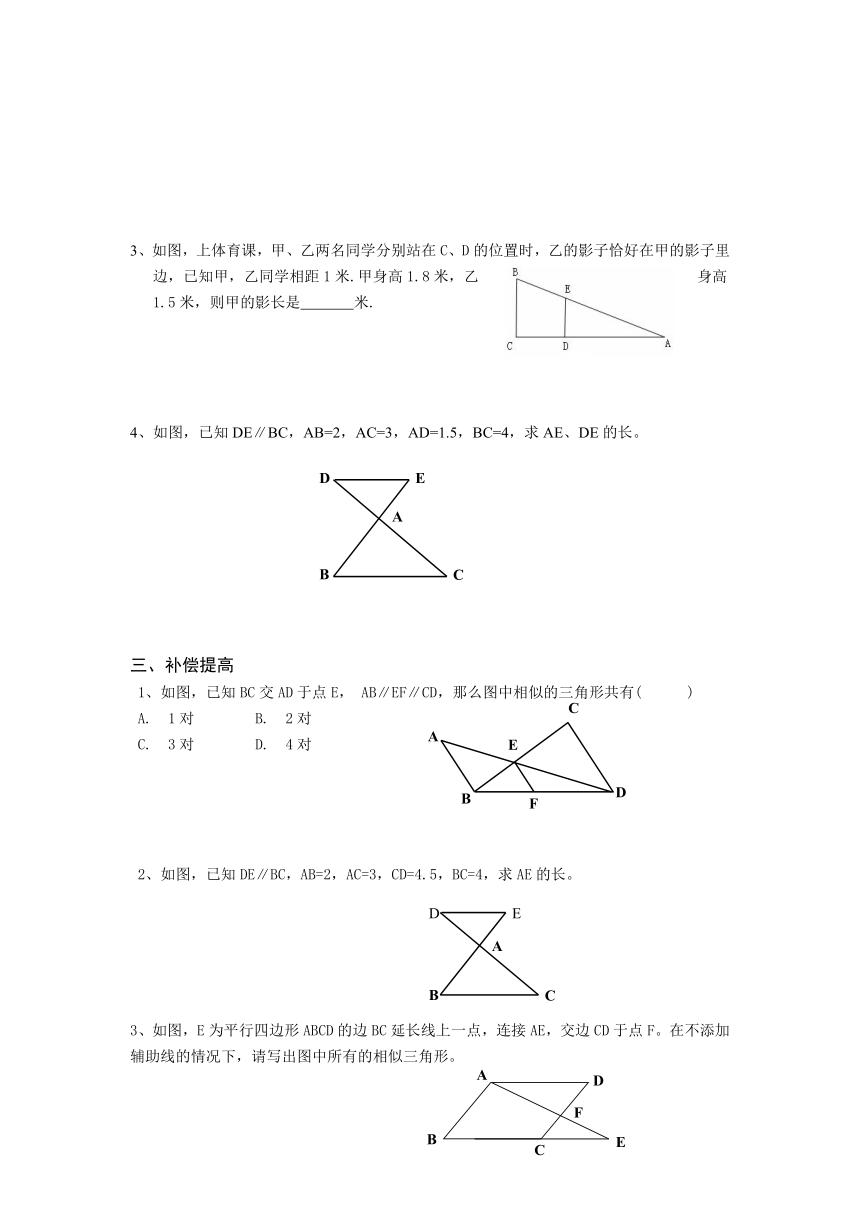
3、如图,上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是
米.
4、如图,已知DE∥BC,AB=2,AC=3,AD=1.5,BC=4,求AE、DE的长。
三、补偿提高
1、如图,已知BC交AD于点E,
AB∥EF∥CD,那么图中相似的三角形共有(
)
A.
1对
B.
2对
C.
3对
D.
4对
2、如图,已知DE∥BC,AB=2,AC=3,CD=4.5,BC=4,求AE的长。
3、如图,E为平行四边形ABCD的边BC延长线上一点,连接AE,交边CD于点F。在不添加辅助线的情况下,请写出图中所有的相似三角形。
4、如图,梯形ABCD中,AB∥DC,AC交BD于点F,延长AD、BC交于点E,DE=2,AD=3。求DF∶BF的值。
相似三角形的判定(第2课时)
一、教学目标:进一步深化对相似三角形的判定方法的理解,并能够运用相似三角形的判定方法解决相似三角形的有关问题.
二、重点:掌握三边比相等两三角形相似的判定定理,并会用此定理判定两三角形相似.
难点:
探究三角形相似的条件,并用该定理解决问题.
三、学情分析
本节内容是研究相似三角形的判定定理1,研究过程中类比三角形全等的判定方法。首先让学生通过画图初步感受到三边的比相等的两三角形相似,然后通过理论严格论证该命题的正确性。
四、自主探究
问题一:试验
1、任意画一个三角形,再画一个三角形,使它的各边长是原来的k(k=2或0.5)倍;
2、比较这两三角形的对应角是否相等(方法:1、可用度量法;2、可剪下一三角形,
用重叠法);
3、这两三角形有什么关系?
4、根据上面讨论,你能得到什么结论?
问题二:证明
1、结合命题,画出图形,写出已知和求证
2、写出证明过程。
五、尝试应用
1、根据下列条件,判断△ABC和△A’B’C’是否相似,并说明理由。
(1)AB=10cm,BC=12cm,AC=15cm;
A’B’=150cm,B’C’=180cm,A’C’=225cm;
(2)AB=4cm,BC=6cm,AC=8cm;
A’B’=12cm,B’C’=18cm,A’C’=21cm。
2、如图,判断两个三角形是否相似。
3、如图,已知,试说明:∠BAD=∠CAE.
4、要制作两个形状相同的三角形框架,其中一个三边长分别是4、5、6,另一个一边长为2,它的另外两边长应当是多少?
六、补偿提高
1、如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上.判断△ABC和△DEF是否相似,并说明理由;
2、如图,
∠DEB
=∠ACB=Rt∠,DE=2,AB=5,BC=3,BD=2.5。
求证:AB平分∠DBC.
相似三角形的判定(第3课时)
一、教学目标:初步掌握“两组对应边的比相等,并且相应的夹角相等的两个三角形相似”的判定方法。
经历两个三角形相似的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程;激发学生探索知识的兴趣,体验数学活动充满着探索性和创造性.
二、重点:掌握判定方法,会运用判定方法判定两个三角形相似.
难点:会准确的运用三角形相似的条件来判定三角形是否相似.
三、学情分析
本节课开始引导学生由三角形全等的条件猜想三角形相似的条件,引起学生的学习兴趣和引出本课主题.再通过作图、测量、计算与比较,验证猜想,最后,从理论上推理论证了三角形相似的判定定理2.练习的设计由易到难,注重了对边和角的位置关系的训练.
四、自主探究
问题一:
1、作图:
(1)任意画△ABC;
(2)作∠MA|N=∠A;
(3)在射线A|M上截取A|D=2AB,在射线A|N上截取A|E=2AC
(4)连接DE.
2、测量BC和B|C|的长度并计算它们的比值,你有什么发现?
3、度量∠B和∠B|,∠C和∠C|的度数,它们分别相等吗?
问题二:
证明:两个三角形的两组对应边的比相等,且它们的夹角相等,那么这两个三角形相似.
五、尝试应用
1.根据下列条件,判断两三角形是否相似,并说明理由:
(1)在△ABC中,∠A=120°,AB=7cm,AC=14cm;
在△A|B|C|中,∠A|=120°,A|B|=3cm,A|C|=6cm.
(2)在△ABC中,∠B=30°,AB=5cm,AC=4cm;
在△A|B|C|中,∠B|=30°,A|B|=10cm,A|C|=8cm.
2.已知:
如图,AB?AC=AD?AE,且∠1=∠2,
求证:△ABC∽△AED.
六、补偿提高
1.如图,在△ABC中,点D在AB上,请再添一个适当的条件,使△ADC∽△ACB,那么可添加的条件是
.
2.如图,在正方形ABCD中,E为AB的中点,BF=BC,试判断与△AED相似的三角形.并说明理由。
3.如图,ΔABC与ΔADB中,∠ABC=∠ADB=90°,AC=5cm,AB=4cm,如果图中的两个直角三角形相似,求AD的长.
七、小结与作业
1、学生小结:
2、必做题:教材P45练习2.
3、选做题:
如图,在△
ABC中,∠
C=90°,BC=8cm,4AC一3BC=0,点P从B出发,沿BC方向以2cm/s的速度移动,点Q从C出发,沿CA方向以lcm/s的速度移动,若P,Q分别从B,C同时出发,经过多长时间,△CBA与△CPQ相似?
相似三角形的判定
一、教学目标:初步掌握“两角对应相等,两个三角形相似”的判定方法.
二、重点:掌握判定方法,会运用判定方法判定两个三角形相似.
难点:会准确的运用两个三角形相似的条件来判定三角形是否相似.
三、学情分析:本节课主要是探究相似三角形的判定方法3,由于上两节课已经学习了探究两个三角形相似的判定引例﹑判定方法1﹑判定方法2,因此本课教学力求使探究途径多元化,把学生利用刻度尺、量角器等作图工具作静态探究与应用“几何画板”等计算机软件作动态探究有机结合起来,让学生充分感受探究的全面性,丰富探究的内涵。协同式小组合作学习的开展不仅提高了数学实验的效率,而且培养了学生的合作能力。
四、自主探究
问题一
1、与同伴合作,一人先画△ABC,另一人再画△A`B`C`,使得∠A=
∠A`,
∠B=
∠B`.
2、比较你们所画的两个三角形,
∠C=
∠C`吗?
3、度量边长,计算,,,你有什么发现?
4、猜想:两个三角形至少有几个角对应相等,才能保证这两个三角形相似?
5、已知:
如图,在△ABC和△A’B’C’中,
∠A=∠A’,∠B=∠B’。
求证:△ABC∽△A’B’C’。
问题二
思考:对于两个直角三角形,我们用“HL”判定它们全等。那么满足斜边之比等于一直角边的比两三角形相似吗?
五、尝试应用
1、下列图形中两个三角形是否相似?
2、判断题:
⑴所有的直角三角形都相似
.
⑵有一个锐角对应相等的两直角三角形相似.
⑶所有的等边三角形都相似.
⑷所有的等腰直角三角形都相似.
⑸顶角相等的两个等腰三角形相似.
⑹有一个角相等的两个等腰三角形相似.
3、如图,弦AB和CD相交于OO内一点P,
求证:PA
?
PB
=
PC?PD
六、补偿提高
1、
已知如图直线BE、DC交于A
,
∠E=
∠C
求证:DA·AC=AB·AE
2、已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
A
B
D
C
E
F
B
A
D
C
E
F
E
A
B
C
D
B
F
C
A
E
D
E
A
B
C
D
E
C
B
D
A
F
B
A
F
C
D
E
A
C
B
F
E
D
P1
P2
P3
P4
P5
30o
A
C
B
55o
30o
30o
30o
30o
O
?
D
P
C
B
A
D
E
A
B
C
1
2
一、教学目标
1.
通过一些具体情境,深化对相似三角形的认识和理解;
2.
掌握并理解平行线分线段成比例定理;
3.
掌握平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似和相似三角形的判定方法,并能运用这个定理进行相似三角形的判定.
二、重点:运用相似三角形的基本定理和判定方法进行证明.
难点:
对“平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似”这一定理的两种情形的理解与掌握.
三、学情分析
相似三角形的判定既是本章的重点,也是整个初中几何的重点。同时,在我们的生活中相似图形的应用也比较广泛。由于有了相似图形、相似多边形和全等三角形的基础,学生应不难理解。
四、自主探究
问题一:相似三角形的概念及表示
1、
什么叫相似三角形?
2、怎样表示两三角形相似?
3、什么是三角形的相似比?
4、如果相似比k=1,两三角形有怎样的关系?
问题二:平行线分线段成比例定理
1、已知如图,直线,直线分别交于点A、B、C、D、E、F.
(1)分别测量线段AB、BC、DE、EF的长度;
(2)计算,的值,你有什么发现?
(3)任意移动,再测量DE、EF的长度,并计算的值,你又有什么发现?
(4)任意平移,再测量AB、BC、DE、EF的长度,计算,的值,上述规律还成立吗?
(5)验证,成立吗?
(6)由上述探究,你能发现什么规律?
2、(1)若1中的相交于上点A,如图,你会得到什么结论?
(2)若1中的相交于上点A,如图,你会得到什么结论?
(3)把(1)中的看成平行于△ABC的边BC的直线,把(2)中的看成平行于△ABC的边BC的直线,你会得到什么结论?
问题三:相似三角形的预备定理
1、在△ABC中,DE∥BC,分别交AB,AC于点D,E,△ADE与△ABC有什么关系?
2、由上题,请你归纳结论.
3、【引申】上述结论中,如果平行线与其他两边延长线相交结论仍成立,你能画出正确的图形吗?
二、尝试应用
1.如图,已知,那么下列结论正确的是(
)
A.
B.
C.
D.
2、如图,在平行四边形ABCD中,E是AD上一点,连结CE并延长交BA的延长线于点F,则下列结论中错误的是
(
)
A.∠AEF=∠DEC
B.FA:CD=AE:BC
C.FA:AB=FE:EC
D.AB=DC
3、如图,上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是
米.
4、如图,已知DE∥BC,AB=2,AC=3,AD=1.5,BC=4,求AE、DE的长。
三、补偿提高
1、如图,已知BC交AD于点E,
AB∥EF∥CD,那么图中相似的三角形共有(
)
A.
1对
B.
2对
C.
3对
D.
4对
2、如图,已知DE∥BC,AB=2,AC=3,CD=4.5,BC=4,求AE的长。
3、如图,E为平行四边形ABCD的边BC延长线上一点,连接AE,交边CD于点F。在不添加辅助线的情况下,请写出图中所有的相似三角形。
4、如图,梯形ABCD中,AB∥DC,AC交BD于点F,延长AD、BC交于点E,DE=2,AD=3。求DF∶BF的值。
相似三角形的判定(第2课时)
一、教学目标:进一步深化对相似三角形的判定方法的理解,并能够运用相似三角形的判定方法解决相似三角形的有关问题.
二、重点:掌握三边比相等两三角形相似的判定定理,并会用此定理判定两三角形相似.
难点:
探究三角形相似的条件,并用该定理解决问题.
三、学情分析
本节内容是研究相似三角形的判定定理1,研究过程中类比三角形全等的判定方法。首先让学生通过画图初步感受到三边的比相等的两三角形相似,然后通过理论严格论证该命题的正确性。
四、自主探究
问题一:试验
1、任意画一个三角形,再画一个三角形,使它的各边长是原来的k(k=2或0.5)倍;
2、比较这两三角形的对应角是否相等(方法:1、可用度量法;2、可剪下一三角形,
用重叠法);
3、这两三角形有什么关系?
4、根据上面讨论,你能得到什么结论?
问题二:证明
1、结合命题,画出图形,写出已知和求证
2、写出证明过程。
五、尝试应用
1、根据下列条件,判断△ABC和△A’B’C’是否相似,并说明理由。
(1)AB=10cm,BC=12cm,AC=15cm;
A’B’=150cm,B’C’=180cm,A’C’=225cm;
(2)AB=4cm,BC=6cm,AC=8cm;
A’B’=12cm,B’C’=18cm,A’C’=21cm。
2、如图,判断两个三角形是否相似。
3、如图,已知,试说明:∠BAD=∠CAE.
4、要制作两个形状相同的三角形框架,其中一个三边长分别是4、5、6,另一个一边长为2,它的另外两边长应当是多少?
六、补偿提高
1、如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上.判断△ABC和△DEF是否相似,并说明理由;
2、如图,
∠DEB
=∠ACB=Rt∠,DE=2,AB=5,BC=3,BD=2.5。
求证:AB平分∠DBC.
相似三角形的判定(第3课时)
一、教学目标:初步掌握“两组对应边的比相等,并且相应的夹角相等的两个三角形相似”的判定方法。
经历两个三角形相似的探索过程,体验用类比、实验操作、分析归纳得出数学结论的过程;激发学生探索知识的兴趣,体验数学活动充满着探索性和创造性.
二、重点:掌握判定方法,会运用判定方法判定两个三角形相似.
难点:会准确的运用三角形相似的条件来判定三角形是否相似.
三、学情分析
本节课开始引导学生由三角形全等的条件猜想三角形相似的条件,引起学生的学习兴趣和引出本课主题.再通过作图、测量、计算与比较,验证猜想,最后,从理论上推理论证了三角形相似的判定定理2.练习的设计由易到难,注重了对边和角的位置关系的训练.
四、自主探究
问题一:
1、作图:
(1)任意画△ABC;
(2)作∠MA|N=∠A;
(3)在射线A|M上截取A|D=2AB,在射线A|N上截取A|E=2AC
(4)连接DE.
2、测量BC和B|C|的长度并计算它们的比值,你有什么发现?
3、度量∠B和∠B|,∠C和∠C|的度数,它们分别相等吗?
问题二:
证明:两个三角形的两组对应边的比相等,且它们的夹角相等,那么这两个三角形相似.
五、尝试应用
1.根据下列条件,判断两三角形是否相似,并说明理由:
(1)在△ABC中,∠A=120°,AB=7cm,AC=14cm;
在△A|B|C|中,∠A|=120°,A|B|=3cm,A|C|=6cm.
(2)在△ABC中,∠B=30°,AB=5cm,AC=4cm;
在△A|B|C|中,∠B|=30°,A|B|=10cm,A|C|=8cm.
2.已知:
如图,AB?AC=AD?AE,且∠1=∠2,
求证:△ABC∽△AED.
六、补偿提高
1.如图,在△ABC中,点D在AB上,请再添一个适当的条件,使△ADC∽△ACB,那么可添加的条件是
.
2.如图,在正方形ABCD中,E为AB的中点,BF=BC,试判断与△AED相似的三角形.并说明理由。
3.如图,ΔABC与ΔADB中,∠ABC=∠ADB=90°,AC=5cm,AB=4cm,如果图中的两个直角三角形相似,求AD的长.
七、小结与作业
1、学生小结:
2、必做题:教材P45练习2.
3、选做题:
如图,在△
ABC中,∠
C=90°,BC=8cm,4AC一3BC=0,点P从B出发,沿BC方向以2cm/s的速度移动,点Q从C出发,沿CA方向以lcm/s的速度移动,若P,Q分别从B,C同时出发,经过多长时间,△CBA与△CPQ相似?
相似三角形的判定
一、教学目标:初步掌握“两角对应相等,两个三角形相似”的判定方法.
二、重点:掌握判定方法,会运用判定方法判定两个三角形相似.
难点:会准确的运用两个三角形相似的条件来判定三角形是否相似.
三、学情分析:本节课主要是探究相似三角形的判定方法3,由于上两节课已经学习了探究两个三角形相似的判定引例﹑判定方法1﹑判定方法2,因此本课教学力求使探究途径多元化,把学生利用刻度尺、量角器等作图工具作静态探究与应用“几何画板”等计算机软件作动态探究有机结合起来,让学生充分感受探究的全面性,丰富探究的内涵。协同式小组合作学习的开展不仅提高了数学实验的效率,而且培养了学生的合作能力。
四、自主探究
问题一
1、与同伴合作,一人先画△ABC,另一人再画△A`B`C`,使得∠A=
∠A`,
∠B=
∠B`.
2、比较你们所画的两个三角形,
∠C=
∠C`吗?
3、度量边长,计算,,,你有什么发现?
4、猜想:两个三角形至少有几个角对应相等,才能保证这两个三角形相似?
5、已知:
如图,在△ABC和△A’B’C’中,
∠A=∠A’,∠B=∠B’。
求证:△ABC∽△A’B’C’。
问题二
思考:对于两个直角三角形,我们用“HL”判定它们全等。那么满足斜边之比等于一直角边的比两三角形相似吗?
五、尝试应用
1、下列图形中两个三角形是否相似?
2、判断题:
⑴所有的直角三角形都相似
.
⑵有一个锐角对应相等的两直角三角形相似.
⑶所有的等边三角形都相似.
⑷所有的等腰直角三角形都相似.
⑸顶角相等的两个等腰三角形相似.
⑹有一个角相等的两个等腰三角形相似.
3、如图,弦AB和CD相交于OO内一点P,
求证:PA
?
PB
=
PC?PD
六、补偿提高
1、
已知如图直线BE、DC交于A
,
∠E=
∠C
求证:DA·AC=AB·AE
2、已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE.
A
B
D
C
E
F
B
A
D
C
E
F
E
A
B
C
D
B
F
C
A
E
D
E
A
B
C
D
E
C
B
D
A
F
B
A
F
C
D
E
A
C
B
F
E
D
P1
P2
P3
P4
P5
30o
A
C
B
55o
30o
30o
30o
30o
O
?
D
P
C
B
A
D
E
A
B
C
1
2
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
