冀教版初中数学八年级上册 13.3 全等三角形的判定 课件(16张)
文档属性
| 名称 | 冀教版初中数学八年级上册 13.3 全等三角形的判定 课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
13.3
三角形全等的判定
(第1课时)
创设情境,导入新知
那么:①AB=DE
③
AC=DF
②
BC=EF
④
∠A=
∠D
⑤
∠B=∠E
⑥
∠C=
∠F
如果:△ABC
≌△
DEF
D
E
F
A
B
C
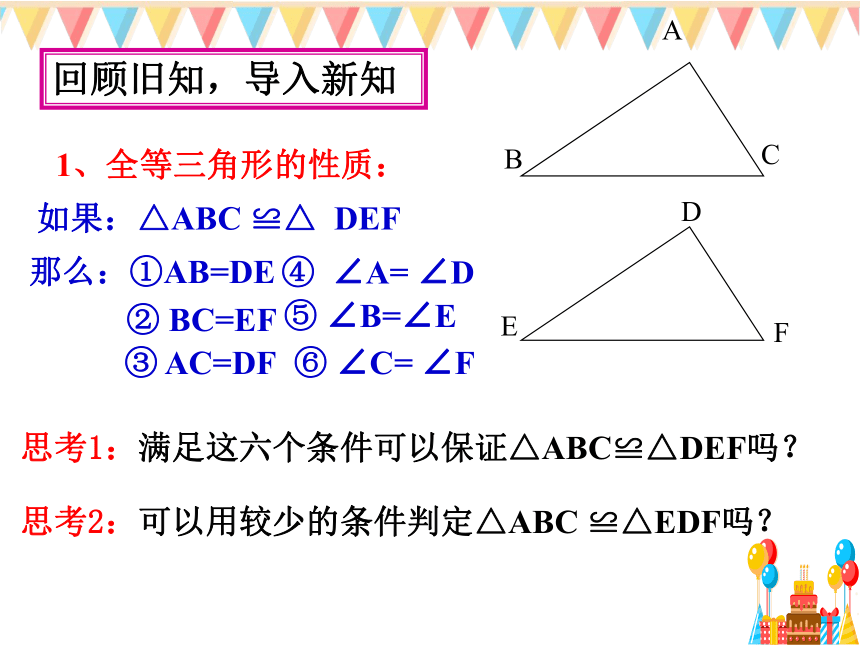
1、全等三角形的性质:
回顾旧知,导入新知
思考1:满足这六个条件可以保证△ABC≌△DEF吗?
思考2:可以用较少的条件判定△ABC
≌△EDF吗?
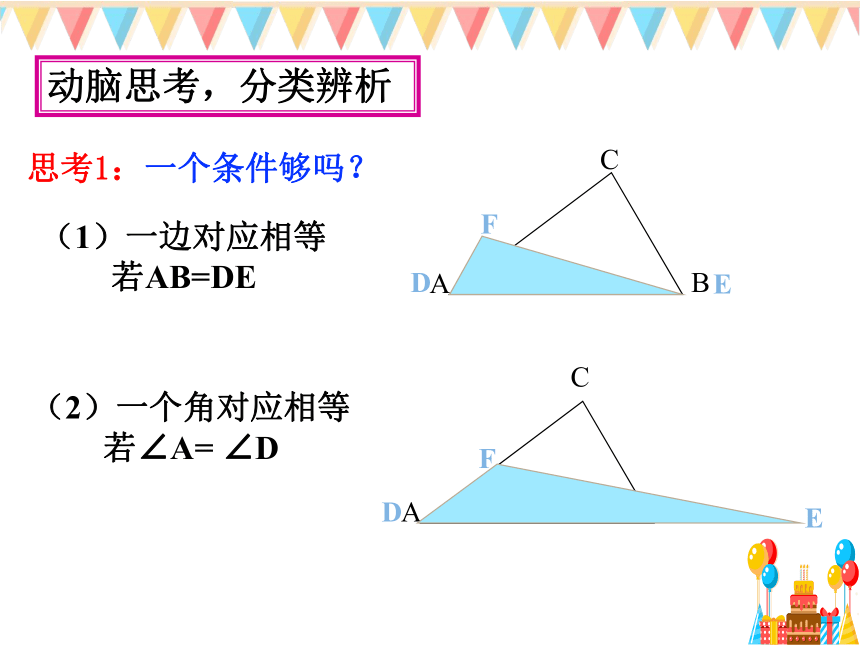
(1)一边对应相等
若AB=DE
C
A
B
E
D
F
(2)一个角对应相等若∠A=
∠D
C
A
B
E
D
F
动脑思考,分类辨析
思考1:一个条件够吗?
(1)两条边对应相等
若AB=DE,AC=DF
C
A
C
A
C
A
B
E
D
F
E
D
F
E
D
F
(2)一条边和一个角对应相等
若AB=DE,∠A=
∠D
(3)两个角对应相等
若∠A=
∠D,∠C=
∠AFE
B
B
动脑思考,分类辨析
思考2:两个条件够吗?
①
三角对应相等
②
三边对应相等
③
两边一角对应相等
④
两角一边对应相等
三个条件
思考3:当满足三个条件时,
可判定两个三角形
全等吗?满足三个条件时,又分为几种情况呢?
动脑思考,分类辨析
思考4:当三边对应相等时,可判定两个三角形全等吗?
探究活动1:
分别用黄色、绿色、蓝色小棒围成两个三角形,观察比较所得的三角形是否全等
?(相同颜色的小棒长度相同)
探究活动2:
分别用红色、绿色、蓝色小棒围成两个三角形,观察比较所得的三角形是否全等
?
动手操作,验证猜想
探究活动3:
任取一组能构成三角形的小棒,同一小组用同一组颜色围成两个三角形,观察比较所得三角形是否全等?
基本事实一:
如果两个三角形的三边对应相等,那么这两个三角形全等。
简写为“边边边”或“SSS”
动脑思考,得出结论
A
B
C
D
E
F
符号语言:
在△ABC
与
△
DEF中:
AB
=ED
∵
AC
=DF
BC
=EF
∴ △ABC
≌△DEF(SSS)
三角形的三边长度确定,它的形状和大小就完全
确定了,所以三角形就具有了稳定性.
例1、已知:如图,AB=AC,
DB=DC,求证:△ABD≌△ACD
A
B
C
D
在△ABD和△ACD中,
AB=AC
(已知)
DB=DC
(已知)
AD=AD
(公共边)
∴△ABD≌△ACD
(SSS)
∴
∠B
=∠C
(全等三角形的对应角相等)
应用所学,例题解析:
求证:∠B
=∠C
1、如图,AB=EF,AC=DE,要使△ABC≌△EFD还需要什么条件?
BC=FD
或
BF=CD
A
B
C
D
E
F
学以致用,变式练习1:
1、已知:
如图,AB=EF,AC=ED,
BF=CD
求证:△ABC≌△EFD
证明:∵
BF=CD
∴BF+FC=CD+FC(等式性质)
即
BC=FD
在△ABC和△FDE
中
AB=EF(已知)
AC=DE(已知)
BC=FD(已证)
∴△ABC≌△EFD(SSS)
∴
∠A=∠E
(全等三角形的对应角相等)
A
B
C
D
E
F
求证:∠A
=∠E
学以致用,变式练习1:
已知:如图,AB=AD,AC=AE,BC=DE.
求证:∠BAD
=∠CAE
A
C
D
B
E
证明:在△ABC和△ADE中
BC=DE(已知)
AB=AD
(
)
AC=AE
(
)
已知
已知
∴△ABC≌△ADE
(SSS)
∴
∠BAC
=∠DAE
(全等三角形的对应角相等)
∴
∠BAC
+∠CAD
=∠DAE+
∠CAD
(等式的性质)
即:
∠BAD
=∠CAE
学以致用,变式练习2:
回顾并观看尺规作图作一个角等于已知角,说一说作法的依据。
应用新知,拓展延伸:
回顾反思,归纳提升:
1、通过今天学习初步体会到探索一个基本事实的过程
2、通过实践与探索得到了一个基本事实,
即:三边对应相等的两个三角形全等
3、掌握了利用“边边边”证明三角形全等的方法及书
面表达,同时也收获了证明两个角相等的又一方法。
4、通过三个题目的学习初步感受了几何图形的三种
基本变换,即:翻折、平移、旋转
学以致用,拓展延伸:
已知:如图,AB=CD,AD=CB.求证:AB∥CD
A
D
B
C
在△ABD和△CDB中,
AB=CD
(已知)
AD=CB
(已知)
BD=DB
(公共边)
∴△ABD≌△CDB
(SSS)
证明:连接BD
∴
∠ABD
=∠CDB
(全等三角形的对应角相等)
∴AB∥CD
(内错角相等,两直线平行)
13.3
三角形全等的判定
(第1课时)
创设情境,导入新知
那么:①AB=DE
③
AC=DF
②
BC=EF
④
∠A=
∠D
⑤
∠B=∠E
⑥
∠C=
∠F
如果:△ABC
≌△
DEF
D
E
F
A
B
C
1、全等三角形的性质:
回顾旧知,导入新知
思考1:满足这六个条件可以保证△ABC≌△DEF吗?
思考2:可以用较少的条件判定△ABC
≌△EDF吗?
(1)一边对应相等
若AB=DE
C
A
B
E
D
F
(2)一个角对应相等若∠A=
∠D
C
A
B
E
D
F
动脑思考,分类辨析
思考1:一个条件够吗?
(1)两条边对应相等
若AB=DE,AC=DF
C
A
C
A
C
A
B
E
D
F
E
D
F
E
D
F
(2)一条边和一个角对应相等
若AB=DE,∠A=
∠D
(3)两个角对应相等
若∠A=
∠D,∠C=
∠AFE
B
B
动脑思考,分类辨析
思考2:两个条件够吗?
①
三角对应相等
②
三边对应相等
③
两边一角对应相等
④
两角一边对应相等
三个条件
思考3:当满足三个条件时,
可判定两个三角形
全等吗?满足三个条件时,又分为几种情况呢?
动脑思考,分类辨析
思考4:当三边对应相等时,可判定两个三角形全等吗?
探究活动1:
分别用黄色、绿色、蓝色小棒围成两个三角形,观察比较所得的三角形是否全等
?(相同颜色的小棒长度相同)
探究活动2:
分别用红色、绿色、蓝色小棒围成两个三角形,观察比较所得的三角形是否全等
?
动手操作,验证猜想
探究活动3:
任取一组能构成三角形的小棒,同一小组用同一组颜色围成两个三角形,观察比较所得三角形是否全等?
基本事实一:
如果两个三角形的三边对应相等,那么这两个三角形全等。
简写为“边边边”或“SSS”
动脑思考,得出结论
A
B
C
D
E
F
符号语言:
在△ABC
与
△
DEF中:
AB
=ED
∵
AC
=DF
BC
=EF
∴ △ABC
≌△DEF(SSS)
三角形的三边长度确定,它的形状和大小就完全
确定了,所以三角形就具有了稳定性.
例1、已知:如图,AB=AC,
DB=DC,求证:△ABD≌△ACD
A
B
C
D
在△ABD和△ACD中,
AB=AC
(已知)
DB=DC
(已知)
AD=AD
(公共边)
∴△ABD≌△ACD
(SSS)
∴
∠B
=∠C
(全等三角形的对应角相等)
应用所学,例题解析:
求证:∠B
=∠C
1、如图,AB=EF,AC=DE,要使△ABC≌△EFD还需要什么条件?
BC=FD
或
BF=CD
A
B
C
D
E
F
学以致用,变式练习1:
1、已知:
如图,AB=EF,AC=ED,
BF=CD
求证:△ABC≌△EFD
证明:∵
BF=CD
∴BF+FC=CD+FC(等式性质)
即
BC=FD
在△ABC和△FDE
中
AB=EF(已知)
AC=DE(已知)
BC=FD(已证)
∴△ABC≌△EFD(SSS)
∴
∠A=∠E
(全等三角形的对应角相等)
A
B
C
D
E
F
求证:∠A
=∠E
学以致用,变式练习1:
已知:如图,AB=AD,AC=AE,BC=DE.
求证:∠BAD
=∠CAE
A
C
D
B
E
证明:在△ABC和△ADE中
BC=DE(已知)
AB=AD
(
)
AC=AE
(
)
已知
已知
∴△ABC≌△ADE
(SSS)
∴
∠BAC
=∠DAE
(全等三角形的对应角相等)
∴
∠BAC
+∠CAD
=∠DAE+
∠CAD
(等式的性质)
即:
∠BAD
=∠CAE
学以致用,变式练习2:
回顾并观看尺规作图作一个角等于已知角,说一说作法的依据。
应用新知,拓展延伸:
回顾反思,归纳提升:
1、通过今天学习初步体会到探索一个基本事实的过程
2、通过实践与探索得到了一个基本事实,
即:三边对应相等的两个三角形全等
3、掌握了利用“边边边”证明三角形全等的方法及书
面表达,同时也收获了证明两个角相等的又一方法。
4、通过三个题目的学习初步感受了几何图形的三种
基本变换,即:翻折、平移、旋转
学以致用,拓展延伸:
已知:如图,AB=CD,AD=CB.求证:AB∥CD
A
D
B
C
在△ABD和△CDB中,
AB=CD
(已知)
AD=CB
(已知)
BD=DB
(公共边)
∴△ABD≌△CDB
(SSS)
证明:连接BD
∴
∠ABD
=∠CDB
(全等三角形的对应角相等)
∴AB∥CD
(内错角相等,两直线平行)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
