人教版数学八年级上册14.3.2因式分解-完全平方公式 课件(17张)
文档属性
| 名称 | 人教版数学八年级上册14.3.2因式分解-完全平方公式 课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
运用完全平方公式分解因式
八年级下册
14.3因式分解
二、学习目标
1
熟练地运用完全公式进行因式分解;
掌握因式分解的公式法之完全平方公式;
2
3
学会用不同的方法将多项式因式分解.
提取公因式法:ma+mb+mc=m(a+b+c)
运用公式法:
①
a2-b2=(a+b)(a-b)
练习
把下列各式分解因式
解:原式=ax2(x2-1)
=ax2(x+1)(x-1)
课前复习:1、分解因式学了哪些方法
(有公因式,先提公因式,且因式分解要彻底。
)
解:原式=(x+1)(x-1)
课前复习:
2.除了平方差公式外,还学过了哪些公式?
下面的多项式能用平方差公式分解因式吗?
(1)
a2+2ab+b2 (2)
a2-2ab+b2
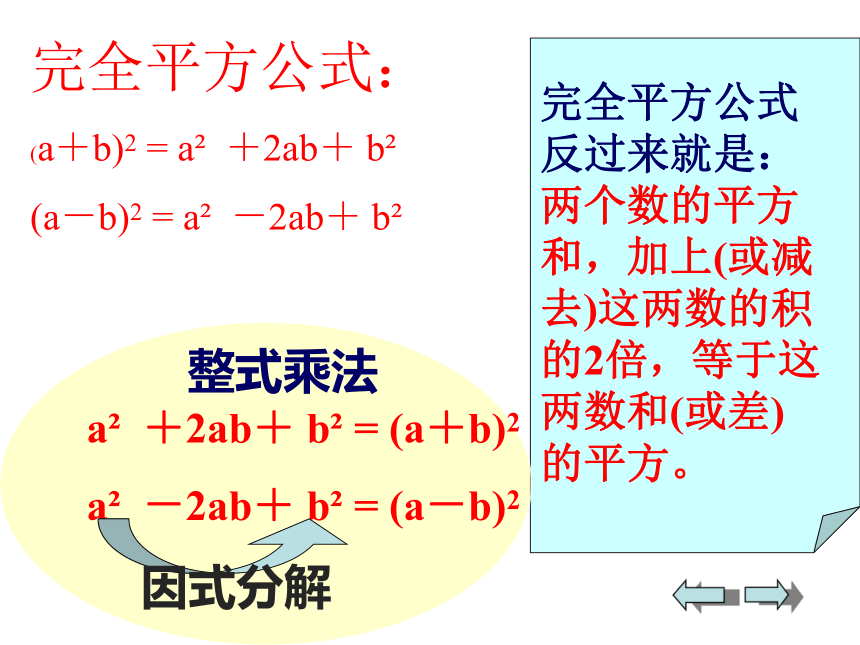
完全平方公式反过来就是:两个数的平方和,加上(或减去)这两数的积的2倍,等于这两数和(或差)的平方。
a?
+2ab+
b?
=
(a+b)2
a?
-2ab+
b?
=
(a-b)2
因式分解
完全平方公式:
(a+b)2
=
a?
+2ab+
b?
(a-b)2
=
a?
-2ab+
b?
整式乘法
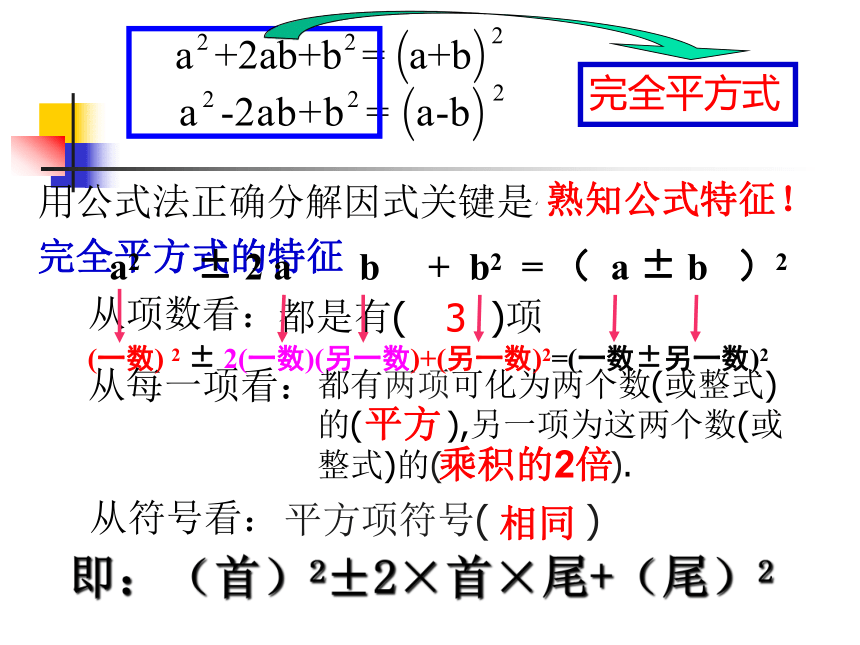
用公式法正确分解因式关键是什么?
熟知公式特征!
完全平方式
完全平方式的特征
3
从项数看:
都是有(
)项
从每一项看:
都有两项可化为两个数(或整式)的(
),另一项为这两个数(或整式)的(
).
从符号看:
平方项符号(
)
a2
±
2
a
b
+
b2
=
(
a
±
b
)2
(一数)
2
±
2(一数)(另一数)+(另一数)2=(一数±另一数)2
平方
乘积的2倍
相同
即:(首)2±2×首×尾+(尾)2
练一练:按照完全平方公式填空:
(
)
2ab
相信自己,我能填!
(
)
(
)
12ab
2m
用完全平方公式分解因式的关键是:在判断一个多项式是不是一个完全平方式。
做一做:下列多项式中,哪些是完全平方式?
是
是
不是
不是
完全平方式
的应用
解:(1)
(1)
例题1分解因式
多项式的各项与公式中的各项分别对应
原式=(4x)2+2×4x×3+32
=(4x+3)2
例题1分解因式
(2)
注意本小题应该先提出一个负号。
完全平方式
的应用
解:原式=-(x2-4xy+4y2)
=-[x2-2·x·2y+(2y)2]
=-(x-2y)2
(2)
解:
例题2
3ax2+6axy+3ay2
(1)
解:
注意啦!首先要考虑能不能提取公因式!
灵活地把(a+b)看成一个整体,这需要你的智慧哟。
(a+b)?-12(a+b)+36
原式=3a(x2+2xy+y2)
=3a(x+y)2
原式=(a+b)2-2·(a+b)·6+62
=(a+b-6)2
判断因式分解正误。
(1)
-x2-2xy-y2=
-(x-y)2
错。应为:
-x2-2xy-y2
=-(
x2+2xy+y2)
=-(x+y)2
(2)a2+2ab-b2
错。此多项式不是完全平方式
辨明真相
=(a-b)2
分解因式:
看谁最快!
解:原式=(2x)2-2·2x·1+12
=(2x-1)2
(1)4x2-4x+1
(2)(m+n)2-4m(m+n)+4m2
解:原式=(m+n)2-2·(m+n)·2m+(2m)2
=(m+n-2m)2
=(n-m)2
1.在括号内填上适当的代数式,使等式成立
(1).a2+6a+______=(a+____)2
(2).16a2+_______+9b2=(_____+_____)2
9
3
±24ab
4a
(±3b)
推广与应用
2.k-6ab+9b2是一个完全平方式,
那么K的值是_____
a2
总结与反思:
1:整式乘法的完全平方公式是:
2:利用完全平方公式分解因式的公式形式是:
3:完全平方公式特点:
含有三项;两平方项的符号同号;首尾2倍中间项
(a±b)2=a2±2ab+b2
a2±2ab+b2=(a±b)2
作业
习题14.3
第三题
再见
谢谢同学们合作
谢谢各位领导及同行指导
运用完全平方公式分解因式
八年级下册
14.3因式分解
二、学习目标
1
熟练地运用完全公式进行因式分解;
掌握因式分解的公式法之完全平方公式;
2
3
学会用不同的方法将多项式因式分解.
提取公因式法:ma+mb+mc=m(a+b+c)
运用公式法:
①
a2-b2=(a+b)(a-b)
练习
把下列各式分解因式
解:原式=ax2(x2-1)
=ax2(x+1)(x-1)
课前复习:1、分解因式学了哪些方法
(有公因式,先提公因式,且因式分解要彻底。
)
解:原式=(x+1)(x-1)
课前复习:
2.除了平方差公式外,还学过了哪些公式?
下面的多项式能用平方差公式分解因式吗?
(1)
a2+2ab+b2 (2)
a2-2ab+b2
完全平方公式反过来就是:两个数的平方和,加上(或减去)这两数的积的2倍,等于这两数和(或差)的平方。
a?
+2ab+
b?
=
(a+b)2
a?
-2ab+
b?
=
(a-b)2
因式分解
完全平方公式:
(a+b)2
=
a?
+2ab+
b?
(a-b)2
=
a?
-2ab+
b?
整式乘法
用公式法正确分解因式关键是什么?
熟知公式特征!
完全平方式
完全平方式的特征
3
从项数看:
都是有(
)项
从每一项看:
都有两项可化为两个数(或整式)的(
),另一项为这两个数(或整式)的(
).
从符号看:
平方项符号(
)
a2
±
2
a
b
+
b2
=
(
a
±
b
)2
(一数)
2
±
2(一数)(另一数)+(另一数)2=(一数±另一数)2
平方
乘积的2倍
相同
即:(首)2±2×首×尾+(尾)2
练一练:按照完全平方公式填空:
(
)
2ab
相信自己,我能填!
(
)
(
)
12ab
2m
用完全平方公式分解因式的关键是:在判断一个多项式是不是一个完全平方式。
做一做:下列多项式中,哪些是完全平方式?
是
是
不是
不是
完全平方式
的应用
解:(1)
(1)
例题1分解因式
多项式的各项与公式中的各项分别对应
原式=(4x)2+2×4x×3+32
=(4x+3)2
例题1分解因式
(2)
注意本小题应该先提出一个负号。
完全平方式
的应用
解:原式=-(x2-4xy+4y2)
=-[x2-2·x·2y+(2y)2]
=-(x-2y)2
(2)
解:
例题2
3ax2+6axy+3ay2
(1)
解:
注意啦!首先要考虑能不能提取公因式!
灵活地把(a+b)看成一个整体,这需要你的智慧哟。
(a+b)?-12(a+b)+36
原式=3a(x2+2xy+y2)
=3a(x+y)2
原式=(a+b)2-2·(a+b)·6+62
=(a+b-6)2
判断因式分解正误。
(1)
-x2-2xy-y2=
-(x-y)2
错。应为:
-x2-2xy-y2
=-(
x2+2xy+y2)
=-(x+y)2
(2)a2+2ab-b2
错。此多项式不是完全平方式
辨明真相
=(a-b)2
分解因式:
看谁最快!
解:原式=(2x)2-2·2x·1+12
=(2x-1)2
(1)4x2-4x+1
(2)(m+n)2-4m(m+n)+4m2
解:原式=(m+n)2-2·(m+n)·2m+(2m)2
=(m+n-2m)2
=(n-m)2
1.在括号内填上适当的代数式,使等式成立
(1).a2+6a+______=(a+____)2
(2).16a2+_______+9b2=(_____+_____)2
9
3
±24ab
4a
(±3b)
推广与应用
2.k-6ab+9b2是一个完全平方式,
那么K的值是_____
a2
总结与反思:
1:整式乘法的完全平方公式是:
2:利用完全平方公式分解因式的公式形式是:
3:完全平方公式特点:
含有三项;两平方项的符号同号;首尾2倍中间项
(a±b)2=a2±2ab+b2
a2±2ab+b2=(a±b)2
作业
习题14.3
第三题
再见
谢谢同学们合作
谢谢各位领导及同行指导
