2020-2021学年山东菏泽八年级上数学第二次月考试卷(word版 含解析)
文档属性
| 名称 | 2020-2021学年山东菏泽八年级上数学第二次月考试卷(word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 601.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 11:24:50 | ||
图片预览




文档简介
2020-2021学年山东菏泽八年级上数学月考试卷
一、选择题
?
1. 下面四大手机品牌图标中,轴对称图形的是(? ? ? ? )
A. B.
C. D.
?
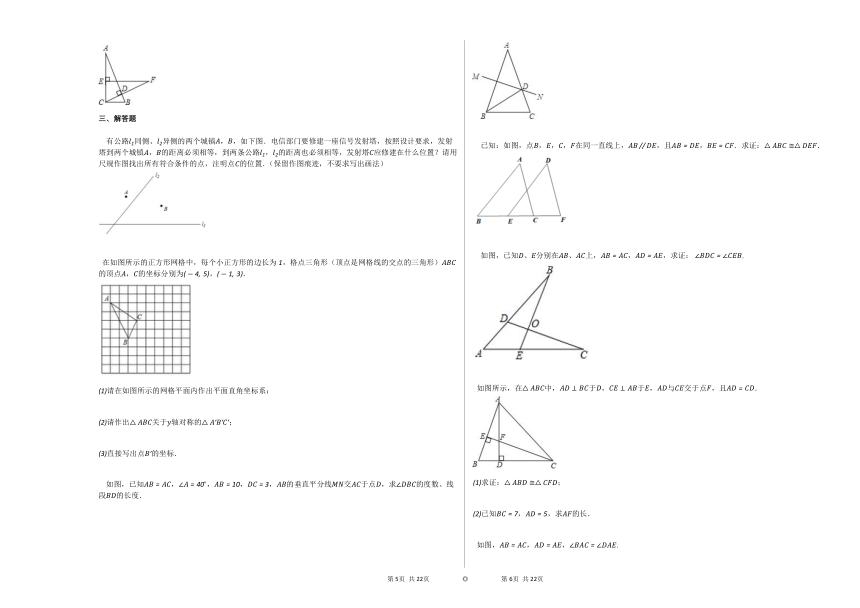
2. 如图,在△ABC中,∠C=31?,∠ABC的平分线BD交AC于点D.如果DE垂直平分BC,那么∠A的度数为(? ? ? ? )
A.31? B.62? C.87? D.93?
?
3. 如图, △ABD?△ACE,AE=3cm,AC=5cm,则线段CD的长为(? ? ? ? )
A.2cm B.3cm C.4cm D.5cm
?
4. 如图,Rt△ABC中,∠C=90?,∠B=30?,分别以点A和点B为圆心,大于12AB的长为半径作弧,两弧相交于M,N两点,作直线MN,交BC于点D,连结AD,则∠CAD的度数是(? ? ? ? )
A.20? B.30? C.45? D.60?
?
5. 下列条件能判定△ABC?△DEF的一组是(? ? ? ? )
A.∠A=∠D,∠B=∠E,∠C=∠F
B.AB=DE,BC=EF,∠A=∠D
C.∠A=∠D,∠C=∠F,AC=DF
D.△ABC的周长等于△DEF的周长
?
6. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC?△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.∠B=∠E,∠A=∠D D.BC=DC,∠A=∠D
?
7.
如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为(? ? ? ? )
A.30? B.36? C.40? D.45?
?
8. 如图,点O在△ABC内,连接OA,OB,OC,若对于任意的△ABC,S△OAB=S△OBC=S△OAC都成立,则点O应是(? ? ? ? )
A.△ABC三条高的交点
B.△ABC的三条中线的交点
C.△ABC的三条角平分线的交点
D.△ABC的一条中线与一条角平分线的交点
?
9. 如图,∠E=∠F=90?,∠B=∠C,AE=AF,下列结论:①EM=NF;②NC=FN;③∠FAN=∠EAM;④△ACN?△ABM.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
?
10. 等腰三角形一腰上的高与另一腰的夹角的度数为20?,则顶角的度数是( )
A.70? B.110? C.70?或110? D.20?或160?
二、填空题
?
已知点A(a,?2),B(?3,?b)关于x轴对称,求a+b=________.
?
等腰三角形的一个角是70?,则它的另外两个角的度数是________.
?
如图,AD?//?BC,∠D=100?,CA平分∠BCD,则∠DAC=________.
?
如图,△ABC中,DE垂直平分AC交AB于E,∠A=30?,∠ACB=80?,则∠BCE=________度.
?
如图所示,已知点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC?△FDE,还需添加一个条件,这个条件可以是________.(只需填一个即可)
?
如图,已知AB?//?CF,E为DF的中点,若AB=9cm,CF=5cm,则BD=________cm.
?
如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为________.
?
?
如图,在Rt△ABC中,∠ACB=90?,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AE=________cm.
三、解答题
?
有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
?
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(?4,?5),(?1,?3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)直接写出点B′的坐标.
?
如图,已知AB=AC,∠A=40?,AB=10,DC=3,AB的垂直平分线MN交AC于点D,求∠DBC的度数、线段BD的长度.
?
已知:如图,点B,E,C,F在同一直线上,AB?//?DE,且AB=DE,BE=CF.求证:△ABC?△DEF.
?
如图,已知D、E分别在AB、AC上,AB=AC,AD=AE,求证:?∠BDC=∠CEB.
?
如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD?△CFD;
(2)已知BC=7,AD=5,求AF的长.
?
如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD?△ACE;
(2)若∠1=25?,∠2=30?,求∠3的度数.
?
如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE//BC,分别交AB,AC于点D,E.
(1)△BDO是等腰三角形吗?请说明理由;
(2)若AB=10,AC=6,求△ADE的周长.
参考答案与试题解析
2020-2021学年山东菏泽八年级上数学月考试卷
一、选择题
1.
【答案】
A
【考点】
轴对称图形
【解析】
此题暂无解析
【解答】
解:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,
此题符合轴对称图形定义条件的是A.
故选A?.
2.
【答案】
C
【考点】
线段垂直平分线的性质
角平分线的性质
三角形内角和定理
【解析】
根据垂直平分线和角平分线的性质解答即可.
【解答】
解:∵ 在△ABC中,∠C=31?,DE垂直平分BC,
∴ ∠CBD=∠C=31?.
∵ ∠ABC的平分线BD交AC于点D,
∴ ∠ABC=2×31?=62?,
∴ ∠A=180??62??31?=87?.
故选C.
3.
【答案】
A
【考点】
全等三角形的性质
【解析】
由△ABD?△ACE根据全等三角形的性质可得AB=AC,AD=AE即可求得CD的长度.
【解答】
解:∵ △ABD?△ACE,
∴ AB=AC=5cm,AD=AE=3cm,
∵ CD=AC?AD,
∴ CD=5?3=2cm.
故选A.
4.
【答案】
B
【考点】
作图—基本作图
线段垂直平分线的性质
【解析】
根据内角和定理求得∠BAC=60?,由垂直平分线性质知DA=DB,即∠DAB=∠B=30?,从而得出答案.
【解答】
解:在△ABC中,∵ ∠B=30?,∠C=90?,
∴ ∠BAC=180??∠B?∠C=60?.
由作图可知MN为AB的垂直平分线,
∴ DA=DB,
∴ ∠DAB=∠B=30?,
∴ ∠CAD=∠BAC?∠DAB=30?.
故选B.
5.
【答案】
C
【考点】
全等三角形的判定
【解析】
判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL,结合选项逐一检验.
【解答】
解:A,∠A=∠D,∠B=∠E,∠C=∠F,是AAA,不能判定两三角形全等,故A不符合题意;
B,AB=DE,BC=EF,∠A=∠D,是SSA,不能判定两三角形全等,故B不符合题意;
C,∠A=∠D,∠C=∠F,AC=DF,符合ASA,能判定两三角形全等,故C符合题意;
D,△ABC的周长等于△DEF的周长,三边可能不相等,故D不符合题意.
故选C.
6.
【答案】
D
【考点】
全等三角形的判定
【解析】
根据全等三角形的判定方法分别进行判定即可.
【解答】
解:A,已知AB=DE,再加上条件BC=EC,∠B=∠E可利用SAS证明△ABC?△DEC,故此选项不合题意;
B,已知AB=DE,再加上条件BC=EC,AC=DC可利用SSS证明△ABC?△DEC,故此选项不合题意;
C,已知AB=DE,再加上条件∠B=∠E,∠A=∠D可利用ASA证明△ABC?△DEC,故此选项不合题意;
D,已知AB=DE,再加上条件BC=DC,∠A=∠D不能证明△ABC?△DEC,故此选项符合题意.
故选D.
7.
【答案】
B
【考点】
等腰三角形的判定与性质
【解析】
求出∠BAD=2∠CAD=2∠B=2∠C的关系,利用三角形的内角和是180?,求∠B,
【解答】
解:∵ AB=AC,
∴ ∠B=∠C,
∵ AB=BD,
∴ ∠BAD=∠BDA,
∵ CD=AD,
∴ ∠C=∠CAD,
∵ ∠BAD+∠CAD+∠B+∠C=180?,
∴ 5∠B=180?,
∴ ∠B=36?.
故选B.
8.
【答案】
B
【考点】
全等三角形的性质与判定
三角形的面积
三角形的角平分线、中线和高
【解析】
根据三角形的面积公式,知点B和点C到AO的距离相等,利用全等三角形就可证明AO的延长线和BC的交点即为BC的中点,同理可证明BO、CO也是三角形的中线的一部分.
【解答】
解:延长AO交BC于P,作BE⊥AO于E,作CF⊥AO于F.
∵ S△OAB=S△OAC,
∴ BE=CF.
∵ ∠E=∠CFP=90?,∠BPE=∠CPF,
∴ △BEP?△CFP,
∴ BP=CP,
∴ AO是BC边上的中线.
同理可以证明BO是AC边上的中线,CO是AB边上的中线,
∴ 点O是三角形的三条中线的交点.
故选B.
9.
【答案】
C
【考点】
等腰三角形的性质
全等三角形的判定
【解析】
先证明△AEB?△AFC得∠EAB=∠FAC即可推出③正确,由△AEM?△AFN即可推出①正确,由△CMD?△BND可以推出②错误,由△ACN?△ABM可以推出④正确,由此即可得出结论.
【解答】
解:在△AEB和△AFC中,
∠E=∠F,∠B=∠C,AE=AF,?
∴ △AEB?△AFC(AAS),
∴ ∠EAB=∠FAC,EB=CF,AB=AC,
∴ ∠EAM=∠FAN,故③正确,
在△AEM和△AFN中,
∠E=∠F,AE=AF,∠EAM=∠FAN,?
∴ △AEM?△AFN(ASA),
∴ EM=FN,AM=AN,故①正确,
在△ACN和△ABM中,
∠CAN=∠BAM,∠C=∠B,AN=AM,?
∴ △ACN?△ABM(AAS),故④正确,
根据已知条件无法得到NC=FN,故②错误,
故①③④正确.
故选C.
10.
【答案】
C
【考点】
三角形内角和定理
三角形的外角性质
等腰三角形的性质
【解析】
本题要分情况讨论.当等腰三角形的顶角是钝角或者等腰三角形的顶角是锐角两种情况.
【解答】
解:此题要分情况讨论:
当等腰三角形的顶角是锐角时,腰上的高在其内部,
故顶角是90??20?=70?.
当等腰三角形的顶角是钝角时,腰上的高在外部,
根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是=90?+20?=110?.
故选C.
二、填空题
【答案】
?5
【考点】
关于x轴、y轴对称的点的坐标
【解析】
先根据“于x轴对称的点,横坐标相同,纵坐标互为相反数”求得a,b的值再求代数式的值.
【解答】
解:∵ 点A(a,?2),B(?3,?b)关于x轴对称,
∴ a=?3,b=?2,
∴ a+b=?5.
故答案为:?5.
【答案】
55?、55?或70?、40?
【考点】
三角形内角和定理
等腰三角形的判定与性质
【解析】
已知给出了一个内角是70?,没有明确是顶角还是底角,所以要进行分类讨论,分类后还有用内角和定理去验证每种情况是不是都成立.
【解答】
解:(1)当顶角为70?时,则它的另外两个角的度数是55?,55?;
(2)当底角70?时,则它的另外两个角的度数是70?,40?;
所以另外两个角是55?,55?或70?,40?.
故答案为:55?,55?或70?,40?.
【答案】
40?
【考点】
角平分线的性质
平行线的判定与性质
【解析】
本题主要利用两直线平行,同旁内角互补、两直线平行,内错角相等以及角平分线的定义进行做题.
【解答】
解:∵ AD?//?BC,
∴ ∠BCD=180??∠D=80?.
又CA平分∠BCD,
∴ ∠ACB=12∠BCD=40?,
∴ ∠DAC=∠ACB=40?.
故答案为:40?.
【答案】
50
【考点】
线段垂直平分线的性质
【解析】
根据△ABC中DE垂直平分AC,可求出AE=CE,再根据等腰三角形的性质求出∠ACE=∠A=30?,再根据∠ACB=80?即可解答.
【解答】
解:∵ DE垂直平分AC,∠A=30?,
∴ AE=CE,∠ACE=∠A=30?,
∵ ∠ACB=80?,
∴ ∠BCE=80??30?=50?.
故答案为:50.
【答案】
∠A=∠F或AC?//?EF或BC=DE(答案不唯一)
【考点】
全等三角形的判定
【解析】
要判定△ABC?△FDE,已知AC=FE,AD=BF,则AB=CF,具备了两组边对应相等,故添加∠A=∠F,利用SAS可证全等.(也可添加其它条件).
【解答】
解:增加一个条件:∠A=∠F,
显然能看出,在△ABC和△FDE中,利用SAS可证三角形全等(答案不唯一).
或增加条件AC?//?EF,得到∠A=∠F,同理利用SAS可证三角形全等(答案不唯一).
或增加条件BC=DE,利用SSS可证三角形全等(答案不唯一).
故答案为:∠A=∠F或AC?//?EF或BC=DE(答案不唯一).
【答案】
4
【考点】
全等三角形的性质与判定
平行线的性质
【解析】
先根据平行线的性质求出∠ADE=∠EFC,再由ASA可求出△ADE?△CFE,根据全等三角形的性质即可求出AD的长,再由AB=9cm即可求出BD的长.
【解答】
解:∵ AB?//?CF,
∴ ∠ADE=∠EFC,
∵ ∠AED=∠FEC,E为DF的中点,
∴ △ADE?△CFE,
∴ AD=CF=5cm,
∵ AB=9cm,
∴ BD=9?5=4cm.
故答案为:4.
【答案】
19cm
【考点】
线段垂直平分线的性质
【解析】
由已知条件,利用线段的垂直平分线的性质,得到AD=CD,AC=2AE,结合周长,进行线段的等量代换可得答案.
【解答】
解:∵ DE是AC的垂直平分线,
∴ AD=CD,AC=2AE=6cm,
又∵ △ABD的周长=AB+BD+AD=13cm,
∴ AB+BD+CD=13cm,
即AB+BC=13cm,
∴ △ABC的周长=AB+BC+AC=13+6=19cm.
故答案为:19cm.
【答案】
3
【考点】
全等三角形的性质与判定
【解析】
根据直角三角形的两锐角互余的性质求出∠ECF=∠B,然后利用“角边角”证明△ABC和△FCE全等,根据全等三角形对应边相等可得AC=EF,再根据AE=AC?CE,代入数据计算即可得解.
【解答】
解:∵ ∠ACB=90?,
∴ ∠ECF+∠BCD=90?.
∵ CD⊥AB,
∴ ∠BCD+∠B=90?,
∴ ∠ECF=∠B(等角的余角相等).
在△FCE和△ABC中,
∠ECF=∠B,EC=CB,∠ACB=∠FEC=90?,
∴ △ABC?△FCE(ASA),
∴ AC=EF.
∵ AE=AC?CE,BC=2cm,EF=5cm,
∴ AE=5?2=3(cm).
故答案为:3.
三、解答题
【答案】
解:作图如下:C1,C2就是所求的位置.
【考点】
作图—应用与设计作图
角平分线的性质
线段垂直平分线的性质
【解析】
根据题意知道,点C应满足两个条件,一是在线段AB的垂直平分线上;二是在两条公路夹角的平分线上,所以点C应是它们的交点.
(1)作两条公路夹角的平分线OD或OE;
(2)作线段AB的垂直平分线FG;
则射线OD,OE与直线FG的交点C1,C2就是所求的位置.
【解答】
解:作图如下:C1,C2就是所求的位置.
【答案】
?解:(1)易得y轴在C的右边一个单位,x轴在C的下方3个单位,
作出平面直角坐标系如图所示:
(2)如图,作出A,B,C三点关于y轴对称的三点,顺次连接,
(3)由(2)图象可知,点B′的坐标为(2,?1).
【考点】
平面直角坐标系的相关概念
作图-轴对称变换
坐标与图形变化-对称
【解析】
(1)易得y轴在C的右边一个单位,x轴在C的下方3个单位;
(2)作出A,B,C三点关于y轴对称的三点,顺次连接即可;
(3)根据所在象限及距离坐标轴的距离可得相应坐标.
【解答】
?解:(1)易得y轴在C的右边一个单位,x轴在C的下方3个单位,
作出平面直角坐标系如图所示:
(2)如图,作出A,B,C三点关于y轴对称的三点,顺次连接,
(3)由(2)图象可知,点B′的坐标为(2,?1).
【答案】
解:∵ AB=AC,∠A=40?,
∴ ∠ABC=∠C=70?.
∵ MN是AB的垂直平分线,
∴ DA=DB,
∴ ∠DBA=∠A=40?,
∴ ∠DBC=30?;
∵ AB=AC,AB=10,DC=3,
∴ BD=DA=10?3=7.
【考点】
等腰三角形的性质
线段垂直平分线的性质
【解析】
根据三角形内角和定理求出∠ABC的度数,根据线段的垂直平分线的性质得到∠DBA的度数,DA=DB,计算即可.
【解答】
解:∵ AB=AC,∠A=40?,
∴ ∠ABC=∠C=70?.
∵ MN是AB的垂直平分线,
∴ DA=DB,
∴ ∠DBA=∠A=40?,
∴ ∠DBC=30?;
∵ AB=AC,AB=10,DC=3,
∴ BD=DA=10?3=7.
【答案】
证明:∵ AB?//?DE,
∴ ∠B=∠DEF.
∵ BE=CF,
∴ BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
AB=DE,∠B=∠DEF,BC=EF,
∴ △ABC?△DEF(SAS).
【考点】
全等三角形的判定
【解析】
根据BE=CF得到BC=EF,然后利用SAS判定定理证明△ABC?△DEF即可.
【解答】
证明:∵ AB?//?DE,
∴ ∠B=∠DEF.
∵ BE=CF,
∴ BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
AB=DE,∠B=∠DEF,BC=EF,
∴ △ABC?△DEF(SAS).
【答案】
证明:在△ABE和△ACD中,
AB=AC,∠A=∠A,AE=AD,
∴ △ABE?△ACD(SAS),
∴ ∠ADC=∠AEB,
∴ ∠BDC=∠CEB.
【考点】
全等三角形的判定
全等三角形的性质
【解析】
? ?
【解答】
证明:在△ABE和△ACD中,
AB=AC,∠A=∠A,AE=AD,
∴ △ABE?△ACD(SAS),
∴ ∠ADC=∠AEB,
∴ ∠BDC=∠CEB.
【答案】
(1)证明:∵ AD⊥BC,CE⊥AB,
∴ ∠ADB=∠CDF=∠CEB=90?,
∴ ∠BAD+∠B=∠FCD+∠B=90?,
∴ ∠BAD=∠FCD,
在△ABD和CFD中,
∠ADB=∠CDF,AD=DC,∠BAD=∠DCF,?
∴ △ABD?△CFD(ASA).
(2)解:∵ △ABD?△CFD,
∴ BD=DF.
∵ BC=7,AD=DC=5,
∴ BD=BC?CD=2,
∴ AF=AD?DF=5?2=3.
【考点】
全等三角形的判定
全等三角形的性质
【解析】
(1)由ASA证明△ABD?△COD即可;
(2)理由全等三角形的性质即可解决问题;∵
【解答】
(1)证明:∵ AD⊥BC,CE⊥AB,
∴ ∠ADB=∠CDF=∠CEB=90?,
∴ ∠BAD+∠B=∠FCD+∠B=90?,
∴ ∠BAD=∠FCD,
在△ABD和CFD中,
∠ADB=∠CDF,AD=DC,∠BAD=∠DCF,?
∴ △ABD?△CFD(ASA).
(2)解:∵ △ABD?△CFD,
∴ BD=DF.
∵ BC=7,AD=DC=5,
∴ BD=BC?CD=2,
∴ AF=AD?DF=5?2=3.
【答案】
(1)证明:∵ ∠BAC=∠DAE,
∴ ∠BAC?∠DAC=∠DAE?∠DAC,
∴ ∠1=∠EAC,
在△ABD和△ACE中,
AB=AC∠1=∠EACAD=AE,
∴ △ABD?△ACE(SAS).
(2)解:∵ △ABD?△ACE,
∴ ∠ABD=∠2=30?,
∵ ∠1=25?,
∴ ∠3=∠1+∠ABD=25?+30?=55?.
【考点】
全等三角形的判定
全等三角形的性质
【解析】
(1)利用已知得出∠1=∠EAC,进而借助SAS得出即可;
(2)利用全等三角形的性质得出∠ABD=∠2=30?,再利用三角形的外角得出得出即可.
【解答】
(1)证明:∵ ∠BAC=∠DAE,
∴ ∠BAC?∠DAC=∠DAE?∠DAC,
∴ ∠1=∠EAC,
在△ABD和△ACE中,
AB=AC∠1=∠EACAD=AE,
∴ △ABD?△ACE(SAS).
(2)解:∵ △ABD?△ACE,
∴ ∠ABD=∠2=30?,
∵ ∠1=25?,
∴ ∠3=∠1+∠ABD=25?+30?=55?.
【答案】
解:(1)△BDO是等腰三角形.理由如下:
∵ BO平分∠ABC,
∴ ∠DBO=∠OBC.
∵ DE//BC,
∴ ∠OBC=∠DOB,
∴ ∠DBO=∠DOB,
∴ BD=OD,
∴ △BDO是等腰三角形.
(2)由(1)知,BD=OD,
同理可得,OE=EC,
∴ △ADE的周长=AD+DE+AE
=AD+DO+OE+AE
=AD+DB+AE+EC
=AB+AC
=16.
【考点】
等腰三角形的判定
等腰三角形的性质
平行线的性质
角平分线的定义
【解析】
? ?
? ?
【解答】
解:(1)△BDO是等腰三角形.理由如下:
∵ BO平分∠ABC,
∴ ∠DBO=∠OBC.
∵ DE//BC,
∴ ∠OBC=∠DOB,
∴ ∠DBO=∠DOB,
∴ BD=OD,
∴ △BDO是等腰三角形.
(2)由(1)知,BD=OD,
同理可得,OE=EC,
∴ △ADE的周长=AD+DE+AE
=AD+DO+OE+AE
=AD+DB+AE+EC
=AB+AC
=16.
一、选择题
?
1. 下面四大手机品牌图标中,轴对称图形的是(? ? ? ? )
A. B.
C. D.
?
2. 如图,在△ABC中,∠C=31?,∠ABC的平分线BD交AC于点D.如果DE垂直平分BC,那么∠A的度数为(? ? ? ? )
A.31? B.62? C.87? D.93?
?
3. 如图, △ABD?△ACE,AE=3cm,AC=5cm,则线段CD的长为(? ? ? ? )
A.2cm B.3cm C.4cm D.5cm
?
4. 如图,Rt△ABC中,∠C=90?,∠B=30?,分别以点A和点B为圆心,大于12AB的长为半径作弧,两弧相交于M,N两点,作直线MN,交BC于点D,连结AD,则∠CAD的度数是(? ? ? ? )
A.20? B.30? C.45? D.60?
?
5. 下列条件能判定△ABC?△DEF的一组是(? ? ? ? )
A.∠A=∠D,∠B=∠E,∠C=∠F
B.AB=DE,BC=EF,∠A=∠D
C.∠A=∠D,∠C=∠F,AC=DF
D.△ABC的周长等于△DEF的周长
?
6. 如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC?△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.∠B=∠E,∠A=∠D D.BC=DC,∠A=∠D
?
7.
如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为(? ? ? ? )
A.30? B.36? C.40? D.45?
?
8. 如图,点O在△ABC内,连接OA,OB,OC,若对于任意的△ABC,S△OAB=S△OBC=S△OAC都成立,则点O应是(? ? ? ? )
A.△ABC三条高的交点
B.△ABC的三条中线的交点
C.△ABC的三条角平分线的交点
D.△ABC的一条中线与一条角平分线的交点
?
9. 如图,∠E=∠F=90?,∠B=∠C,AE=AF,下列结论:①EM=NF;②NC=FN;③∠FAN=∠EAM;④△ACN?△ABM.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
?
10. 等腰三角形一腰上的高与另一腰的夹角的度数为20?,则顶角的度数是( )
A.70? B.110? C.70?或110? D.20?或160?
二、填空题
?
已知点A(a,?2),B(?3,?b)关于x轴对称,求a+b=________.
?
等腰三角形的一个角是70?,则它的另外两个角的度数是________.
?
如图,AD?//?BC,∠D=100?,CA平分∠BCD,则∠DAC=________.
?
如图,△ABC中,DE垂直平分AC交AB于E,∠A=30?,∠ACB=80?,则∠BCE=________度.
?
如图所示,已知点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC?△FDE,还需添加一个条件,这个条件可以是________.(只需填一个即可)
?
如图,已知AB?//?CF,E为DF的中点,若AB=9cm,CF=5cm,则BD=________cm.
?
如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为________.
?
?
如图,在Rt△ABC中,∠ACB=90?,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AE=________cm.
三、解答题
?
有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
?
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(?4,?5),(?1,?3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)直接写出点B′的坐标.
?
如图,已知AB=AC,∠A=40?,AB=10,DC=3,AB的垂直平分线MN交AC于点D,求∠DBC的度数、线段BD的长度.
?
已知:如图,点B,E,C,F在同一直线上,AB?//?DE,且AB=DE,BE=CF.求证:△ABC?△DEF.
?
如图,已知D、E分别在AB、AC上,AB=AC,AD=AE,求证:?∠BDC=∠CEB.
?
如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,且AD=CD.
(1)求证:△ABD?△CFD;
(2)已知BC=7,AD=5,求AF的长.
?
如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD?△ACE;
(2)若∠1=25?,∠2=30?,求∠3的度数.
?
如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE//BC,分别交AB,AC于点D,E.
(1)△BDO是等腰三角形吗?请说明理由;
(2)若AB=10,AC=6,求△ADE的周长.
参考答案与试题解析
2020-2021学年山东菏泽八年级上数学月考试卷
一、选择题
1.
【答案】
A
【考点】
轴对称图形
【解析】
此题暂无解析
【解答】
解:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,
此题符合轴对称图形定义条件的是A.
故选A?.
2.
【答案】
C
【考点】
线段垂直平分线的性质
角平分线的性质
三角形内角和定理
【解析】
根据垂直平分线和角平分线的性质解答即可.
【解答】
解:∵ 在△ABC中,∠C=31?,DE垂直平分BC,
∴ ∠CBD=∠C=31?.
∵ ∠ABC的平分线BD交AC于点D,
∴ ∠ABC=2×31?=62?,
∴ ∠A=180??62??31?=87?.
故选C.
3.
【答案】
A
【考点】
全等三角形的性质
【解析】
由△ABD?△ACE根据全等三角形的性质可得AB=AC,AD=AE即可求得CD的长度.
【解答】
解:∵ △ABD?△ACE,
∴ AB=AC=5cm,AD=AE=3cm,
∵ CD=AC?AD,
∴ CD=5?3=2cm.
故选A.
4.
【答案】
B
【考点】
作图—基本作图
线段垂直平分线的性质
【解析】
根据内角和定理求得∠BAC=60?,由垂直平分线性质知DA=DB,即∠DAB=∠B=30?,从而得出答案.
【解答】
解:在△ABC中,∵ ∠B=30?,∠C=90?,
∴ ∠BAC=180??∠B?∠C=60?.
由作图可知MN为AB的垂直平分线,
∴ DA=DB,
∴ ∠DAB=∠B=30?,
∴ ∠CAD=∠BAC?∠DAB=30?.
故选B.
5.
【答案】
C
【考点】
全等三角形的判定
【解析】
判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL,结合选项逐一检验.
【解答】
解:A,∠A=∠D,∠B=∠E,∠C=∠F,是AAA,不能判定两三角形全等,故A不符合题意;
B,AB=DE,BC=EF,∠A=∠D,是SSA,不能判定两三角形全等,故B不符合题意;
C,∠A=∠D,∠C=∠F,AC=DF,符合ASA,能判定两三角形全等,故C符合题意;
D,△ABC的周长等于△DEF的周长,三边可能不相等,故D不符合题意.
故选C.
6.
【答案】
D
【考点】
全等三角形的判定
【解析】
根据全等三角形的判定方法分别进行判定即可.
【解答】
解:A,已知AB=DE,再加上条件BC=EC,∠B=∠E可利用SAS证明△ABC?△DEC,故此选项不合题意;
B,已知AB=DE,再加上条件BC=EC,AC=DC可利用SSS证明△ABC?△DEC,故此选项不合题意;
C,已知AB=DE,再加上条件∠B=∠E,∠A=∠D可利用ASA证明△ABC?△DEC,故此选项不合题意;
D,已知AB=DE,再加上条件BC=DC,∠A=∠D不能证明△ABC?△DEC,故此选项符合题意.
故选D.
7.
【答案】
B
【考点】
等腰三角形的判定与性质
【解析】
求出∠BAD=2∠CAD=2∠B=2∠C的关系,利用三角形的内角和是180?,求∠B,
【解答】
解:∵ AB=AC,
∴ ∠B=∠C,
∵ AB=BD,
∴ ∠BAD=∠BDA,
∵ CD=AD,
∴ ∠C=∠CAD,
∵ ∠BAD+∠CAD+∠B+∠C=180?,
∴ 5∠B=180?,
∴ ∠B=36?.
故选B.
8.
【答案】
B
【考点】
全等三角形的性质与判定
三角形的面积
三角形的角平分线、中线和高
【解析】
根据三角形的面积公式,知点B和点C到AO的距离相等,利用全等三角形就可证明AO的延长线和BC的交点即为BC的中点,同理可证明BO、CO也是三角形的中线的一部分.
【解答】
解:延长AO交BC于P,作BE⊥AO于E,作CF⊥AO于F.
∵ S△OAB=S△OAC,
∴ BE=CF.
∵ ∠E=∠CFP=90?,∠BPE=∠CPF,
∴ △BEP?△CFP,
∴ BP=CP,
∴ AO是BC边上的中线.
同理可以证明BO是AC边上的中线,CO是AB边上的中线,
∴ 点O是三角形的三条中线的交点.
故选B.
9.
【答案】
C
【考点】
等腰三角形的性质
全等三角形的判定
【解析】
先证明△AEB?△AFC得∠EAB=∠FAC即可推出③正确,由△AEM?△AFN即可推出①正确,由△CMD?△BND可以推出②错误,由△ACN?△ABM可以推出④正确,由此即可得出结论.
【解答】
解:在△AEB和△AFC中,
∠E=∠F,∠B=∠C,AE=AF,?
∴ △AEB?△AFC(AAS),
∴ ∠EAB=∠FAC,EB=CF,AB=AC,
∴ ∠EAM=∠FAN,故③正确,
在△AEM和△AFN中,
∠E=∠F,AE=AF,∠EAM=∠FAN,?
∴ △AEM?△AFN(ASA),
∴ EM=FN,AM=AN,故①正确,
在△ACN和△ABM中,
∠CAN=∠BAM,∠C=∠B,AN=AM,?
∴ △ACN?△ABM(AAS),故④正确,
根据已知条件无法得到NC=FN,故②错误,
故①③④正确.
故选C.
10.
【答案】
C
【考点】
三角形内角和定理
三角形的外角性质
等腰三角形的性质
【解析】
本题要分情况讨论.当等腰三角形的顶角是钝角或者等腰三角形的顶角是锐角两种情况.
【解答】
解:此题要分情况讨论:
当等腰三角形的顶角是锐角时,腰上的高在其内部,
故顶角是90??20?=70?.
当等腰三角形的顶角是钝角时,腰上的高在外部,
根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是=90?+20?=110?.
故选C.
二、填空题
【答案】
?5
【考点】
关于x轴、y轴对称的点的坐标
【解析】
先根据“于x轴对称的点,横坐标相同,纵坐标互为相反数”求得a,b的值再求代数式的值.
【解答】
解:∵ 点A(a,?2),B(?3,?b)关于x轴对称,
∴ a=?3,b=?2,
∴ a+b=?5.
故答案为:?5.
【答案】
55?、55?或70?、40?
【考点】
三角形内角和定理
等腰三角形的判定与性质
【解析】
已知给出了一个内角是70?,没有明确是顶角还是底角,所以要进行分类讨论,分类后还有用内角和定理去验证每种情况是不是都成立.
【解答】
解:(1)当顶角为70?时,则它的另外两个角的度数是55?,55?;
(2)当底角70?时,则它的另外两个角的度数是70?,40?;
所以另外两个角是55?,55?或70?,40?.
故答案为:55?,55?或70?,40?.
【答案】
40?
【考点】
角平分线的性质
平行线的判定与性质
【解析】
本题主要利用两直线平行,同旁内角互补、两直线平行,内错角相等以及角平分线的定义进行做题.
【解答】
解:∵ AD?//?BC,
∴ ∠BCD=180??∠D=80?.
又CA平分∠BCD,
∴ ∠ACB=12∠BCD=40?,
∴ ∠DAC=∠ACB=40?.
故答案为:40?.
【答案】
50
【考点】
线段垂直平分线的性质
【解析】
根据△ABC中DE垂直平分AC,可求出AE=CE,再根据等腰三角形的性质求出∠ACE=∠A=30?,再根据∠ACB=80?即可解答.
【解答】
解:∵ DE垂直平分AC,∠A=30?,
∴ AE=CE,∠ACE=∠A=30?,
∵ ∠ACB=80?,
∴ ∠BCE=80??30?=50?.
故答案为:50.
【答案】
∠A=∠F或AC?//?EF或BC=DE(答案不唯一)
【考点】
全等三角形的判定
【解析】
要判定△ABC?△FDE,已知AC=FE,AD=BF,则AB=CF,具备了两组边对应相等,故添加∠A=∠F,利用SAS可证全等.(也可添加其它条件).
【解答】
解:增加一个条件:∠A=∠F,
显然能看出,在△ABC和△FDE中,利用SAS可证三角形全等(答案不唯一).
或增加条件AC?//?EF,得到∠A=∠F,同理利用SAS可证三角形全等(答案不唯一).
或增加条件BC=DE,利用SSS可证三角形全等(答案不唯一).
故答案为:∠A=∠F或AC?//?EF或BC=DE(答案不唯一).
【答案】
4
【考点】
全等三角形的性质与判定
平行线的性质
【解析】
先根据平行线的性质求出∠ADE=∠EFC,再由ASA可求出△ADE?△CFE,根据全等三角形的性质即可求出AD的长,再由AB=9cm即可求出BD的长.
【解答】
解:∵ AB?//?CF,
∴ ∠ADE=∠EFC,
∵ ∠AED=∠FEC,E为DF的中点,
∴ △ADE?△CFE,
∴ AD=CF=5cm,
∵ AB=9cm,
∴ BD=9?5=4cm.
故答案为:4.
【答案】
19cm
【考点】
线段垂直平分线的性质
【解析】
由已知条件,利用线段的垂直平分线的性质,得到AD=CD,AC=2AE,结合周长,进行线段的等量代换可得答案.
【解答】
解:∵ DE是AC的垂直平分线,
∴ AD=CD,AC=2AE=6cm,
又∵ △ABD的周长=AB+BD+AD=13cm,
∴ AB+BD+CD=13cm,
即AB+BC=13cm,
∴ △ABC的周长=AB+BC+AC=13+6=19cm.
故答案为:19cm.
【答案】
3
【考点】
全等三角形的性质与判定
【解析】
根据直角三角形的两锐角互余的性质求出∠ECF=∠B,然后利用“角边角”证明△ABC和△FCE全等,根据全等三角形对应边相等可得AC=EF,再根据AE=AC?CE,代入数据计算即可得解.
【解答】
解:∵ ∠ACB=90?,
∴ ∠ECF+∠BCD=90?.
∵ CD⊥AB,
∴ ∠BCD+∠B=90?,
∴ ∠ECF=∠B(等角的余角相等).
在△FCE和△ABC中,
∠ECF=∠B,EC=CB,∠ACB=∠FEC=90?,
∴ △ABC?△FCE(ASA),
∴ AC=EF.
∵ AE=AC?CE,BC=2cm,EF=5cm,
∴ AE=5?2=3(cm).
故答案为:3.
三、解答题
【答案】
解:作图如下:C1,C2就是所求的位置.
【考点】
作图—应用与设计作图
角平分线的性质
线段垂直平分线的性质
【解析】
根据题意知道,点C应满足两个条件,一是在线段AB的垂直平分线上;二是在两条公路夹角的平分线上,所以点C应是它们的交点.
(1)作两条公路夹角的平分线OD或OE;
(2)作线段AB的垂直平分线FG;
则射线OD,OE与直线FG的交点C1,C2就是所求的位置.
【解答】
解:作图如下:C1,C2就是所求的位置.
【答案】
?解:(1)易得y轴在C的右边一个单位,x轴在C的下方3个单位,
作出平面直角坐标系如图所示:
(2)如图,作出A,B,C三点关于y轴对称的三点,顺次连接,
(3)由(2)图象可知,点B′的坐标为(2,?1).
【考点】
平面直角坐标系的相关概念
作图-轴对称变换
坐标与图形变化-对称
【解析】
(1)易得y轴在C的右边一个单位,x轴在C的下方3个单位;
(2)作出A,B,C三点关于y轴对称的三点,顺次连接即可;
(3)根据所在象限及距离坐标轴的距离可得相应坐标.
【解答】
?解:(1)易得y轴在C的右边一个单位,x轴在C的下方3个单位,
作出平面直角坐标系如图所示:
(2)如图,作出A,B,C三点关于y轴对称的三点,顺次连接,
(3)由(2)图象可知,点B′的坐标为(2,?1).
【答案】
解:∵ AB=AC,∠A=40?,
∴ ∠ABC=∠C=70?.
∵ MN是AB的垂直平分线,
∴ DA=DB,
∴ ∠DBA=∠A=40?,
∴ ∠DBC=30?;
∵ AB=AC,AB=10,DC=3,
∴ BD=DA=10?3=7.
【考点】
等腰三角形的性质
线段垂直平分线的性质
【解析】
根据三角形内角和定理求出∠ABC的度数,根据线段的垂直平分线的性质得到∠DBA的度数,DA=DB,计算即可.
【解答】
解:∵ AB=AC,∠A=40?,
∴ ∠ABC=∠C=70?.
∵ MN是AB的垂直平分线,
∴ DA=DB,
∴ ∠DBA=∠A=40?,
∴ ∠DBC=30?;
∵ AB=AC,AB=10,DC=3,
∴ BD=DA=10?3=7.
【答案】
证明:∵ AB?//?DE,
∴ ∠B=∠DEF.
∵ BE=CF,
∴ BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
AB=DE,∠B=∠DEF,BC=EF,
∴ △ABC?△DEF(SAS).
【考点】
全等三角形的判定
【解析】
根据BE=CF得到BC=EF,然后利用SAS判定定理证明△ABC?△DEF即可.
【解答】
证明:∵ AB?//?DE,
∴ ∠B=∠DEF.
∵ BE=CF,
∴ BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
AB=DE,∠B=∠DEF,BC=EF,
∴ △ABC?△DEF(SAS).
【答案】
证明:在△ABE和△ACD中,
AB=AC,∠A=∠A,AE=AD,
∴ △ABE?△ACD(SAS),
∴ ∠ADC=∠AEB,
∴ ∠BDC=∠CEB.
【考点】
全等三角形的判定
全等三角形的性质
【解析】
? ?
【解答】
证明:在△ABE和△ACD中,
AB=AC,∠A=∠A,AE=AD,
∴ △ABE?△ACD(SAS),
∴ ∠ADC=∠AEB,
∴ ∠BDC=∠CEB.
【答案】
(1)证明:∵ AD⊥BC,CE⊥AB,
∴ ∠ADB=∠CDF=∠CEB=90?,
∴ ∠BAD+∠B=∠FCD+∠B=90?,
∴ ∠BAD=∠FCD,
在△ABD和CFD中,
∠ADB=∠CDF,AD=DC,∠BAD=∠DCF,?
∴ △ABD?△CFD(ASA).
(2)解:∵ △ABD?△CFD,
∴ BD=DF.
∵ BC=7,AD=DC=5,
∴ BD=BC?CD=2,
∴ AF=AD?DF=5?2=3.
【考点】
全等三角形的判定
全等三角形的性质
【解析】
(1)由ASA证明△ABD?△COD即可;
(2)理由全等三角形的性质即可解决问题;∵
【解答】
(1)证明:∵ AD⊥BC,CE⊥AB,
∴ ∠ADB=∠CDF=∠CEB=90?,
∴ ∠BAD+∠B=∠FCD+∠B=90?,
∴ ∠BAD=∠FCD,
在△ABD和CFD中,
∠ADB=∠CDF,AD=DC,∠BAD=∠DCF,?
∴ △ABD?△CFD(ASA).
(2)解:∵ △ABD?△CFD,
∴ BD=DF.
∵ BC=7,AD=DC=5,
∴ BD=BC?CD=2,
∴ AF=AD?DF=5?2=3.
【答案】
(1)证明:∵ ∠BAC=∠DAE,
∴ ∠BAC?∠DAC=∠DAE?∠DAC,
∴ ∠1=∠EAC,
在△ABD和△ACE中,
AB=AC∠1=∠EACAD=AE,
∴ △ABD?△ACE(SAS).
(2)解:∵ △ABD?△ACE,
∴ ∠ABD=∠2=30?,
∵ ∠1=25?,
∴ ∠3=∠1+∠ABD=25?+30?=55?.
【考点】
全等三角形的判定
全等三角形的性质
【解析】
(1)利用已知得出∠1=∠EAC,进而借助SAS得出即可;
(2)利用全等三角形的性质得出∠ABD=∠2=30?,再利用三角形的外角得出得出即可.
【解答】
(1)证明:∵ ∠BAC=∠DAE,
∴ ∠BAC?∠DAC=∠DAE?∠DAC,
∴ ∠1=∠EAC,
在△ABD和△ACE中,
AB=AC∠1=∠EACAD=AE,
∴ △ABD?△ACE(SAS).
(2)解:∵ △ABD?△ACE,
∴ ∠ABD=∠2=30?,
∵ ∠1=25?,
∴ ∠3=∠1+∠ABD=25?+30?=55?.
【答案】
解:(1)△BDO是等腰三角形.理由如下:
∵ BO平分∠ABC,
∴ ∠DBO=∠OBC.
∵ DE//BC,
∴ ∠OBC=∠DOB,
∴ ∠DBO=∠DOB,
∴ BD=OD,
∴ △BDO是等腰三角形.
(2)由(1)知,BD=OD,
同理可得,OE=EC,
∴ △ADE的周长=AD+DE+AE
=AD+DO+OE+AE
=AD+DB+AE+EC
=AB+AC
=16.
【考点】
等腰三角形的判定
等腰三角形的性质
平行线的性质
角平分线的定义
【解析】
? ?
? ?
【解答】
解:(1)△BDO是等腰三角形.理由如下:
∵ BO平分∠ABC,
∴ ∠DBO=∠OBC.
∵ DE//BC,
∴ ∠OBC=∠DOB,
∴ ∠DBO=∠DOB,
∴ BD=OD,
∴ △BDO是等腰三角形.
(2)由(1)知,BD=OD,
同理可得,OE=EC,
∴ △ADE的周长=AD+DE+AE
=AD+DO+OE+AE
=AD+DB+AE+EC
=AB+AC
=16.
同课章节目录
