直线和圆的位置关系

(共17张PPT)
O
A
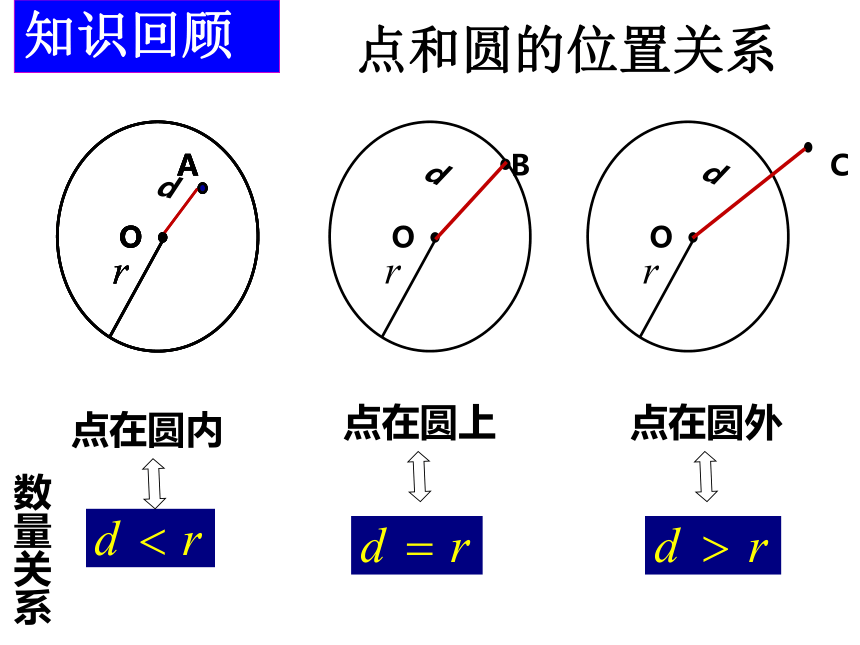
知识回顾
点和圆的位置关系
点在圆内
点在圆上
点在圆外
O
B
O
C
O
A
d
d
O
A
d
O
A
数量关系
如图，在太阳升起的过程中，太阳和地平线会有几种位置关系？我们把太阳看作一个圆，把地平线看作一条直线，由此你能得出直线和圆的位置关系吗？
在纸上画一条直线(地平线),把硬币的边缘看作圆(太阳)在纸上移动硬币.
你能发现直线与圆的公共点个数的变化情况吗？公共点最少时有几个？最多时有几个？
动手做一做
想想:
直线与圆有_____种位置关系，是
用直线与圆的________的个数来定义
的．这也是判断直线 与圆的位置关系
的重要方法.
三
公共点
1.直线与圆最多有两个公共点 （　）
√
×
2.若直线与圆相交,则直线上的点都在圆内( )
3 .若C为⊙O外的一点，则过点C的直线
CD 与 ⊙O 相交或相离（ ）
×
.C
练习1
(3)若AB和⊙O相交,则 .
1.已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
(1)若AB和⊙O相离, 则 ;
(2)若AB和⊙O相切, 则 ;
d > 5cm
d = 5cm
d < 5cm
0cm≤
练习2
2.已知圆的半径等于5,直线l与圆没有交点,则圆
心到直线的距离d的取值范围是 .
d>5
3.已知圆的直径为13cm，设圆心到直线的距离
为d ：
(3)若d= 8 cm ,则直线与圆______, 直线与圆
有____个公共点.
(2)若d=6.5cm ,则直线与圆______, 直线与圆
有____个公共点.
(1)若d=4.5cm ,则直线与圆　　　, 直线与圆
有____个公共点.
相交
相切
相离
两
一
零
练习2
利用圆心到直线的距离与半径的大小关系来判定直线和圆的位置关系
思考：求圆心A到X轴、
Y轴的距离各是多少
A.(-3,-4)
O
X
Y
已知⊙A的直径为6，点A的坐标为（-3，-4），则X轴与⊙A的位置关系是_____, Y轴与⊙A的位置关系是______。
B
C
4
3
相离
相切
练习3
补充：在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm。以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？
(1)r=2cm (2)r=2.4cm (3)r=3cm
B
4
C 3 A
D
解：圆心C到AB的距离d=2.4cm
(1)当r=2cm时,
有d>r,
因此⊙C和AB相离。
5
2.4
思考：图中线段AB的长度为多少？
.
(2)当r=2.4cm 时,
有d=r,
因此⊙C和AB相切。
D
B
C A
2.4
(3)当r=3cm 时，
有d因此⊙C和AB相交。
D
B
C A
2.4
怎样求圆心C到直线AB的距离？
0
d>r
1
d=r
切点
切线
2
d交点
割线
．Ｏ
l
d
r
┐
┐
．ｏ
l
d
r
．O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
归纳小结：
随堂检测
1．⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l　
　与⊙O没有公共点，则d为（　）：
　A．d ＞3 B．d<3 C．d ≤3 D．d =3
2．圆心O到直线的距离等于⊙O的半径，则直线
和⊙O的位置 关系是（　　）：
A．相离 B.相交 C.相切 D.相切或相交
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
与直线BC的位置关系是 ,以A为圆心,以
为半径的圆与直线BC相切.
A
C
√
相离
随堂检测：
5．若⊙O与直线m的距离为d，⊙O 的半径为
r，若d，r是方程
则直线m与⊙O的位置关系是
相离或相交
的两个根，
的两个根，且直线m
1、若d，r是方程
与⊙O的位置关系是相切，则a的值是 。
2、如图：菱形ABCD的边长为5cm，∠B=60°当以
A为圆心的圆与BC相切时，半径是 ，此时
⊙A与CD的位置关系是 。
D
C
B
A
思考题：