北师大版九年级数学上册4.6利用相似三角形测高-假期同步测试(word版含答案)
文档属性
| 名称 | 北师大版九年级数学上册4.6利用相似三角形测高-假期同步测试(word版含答案) |

|
|
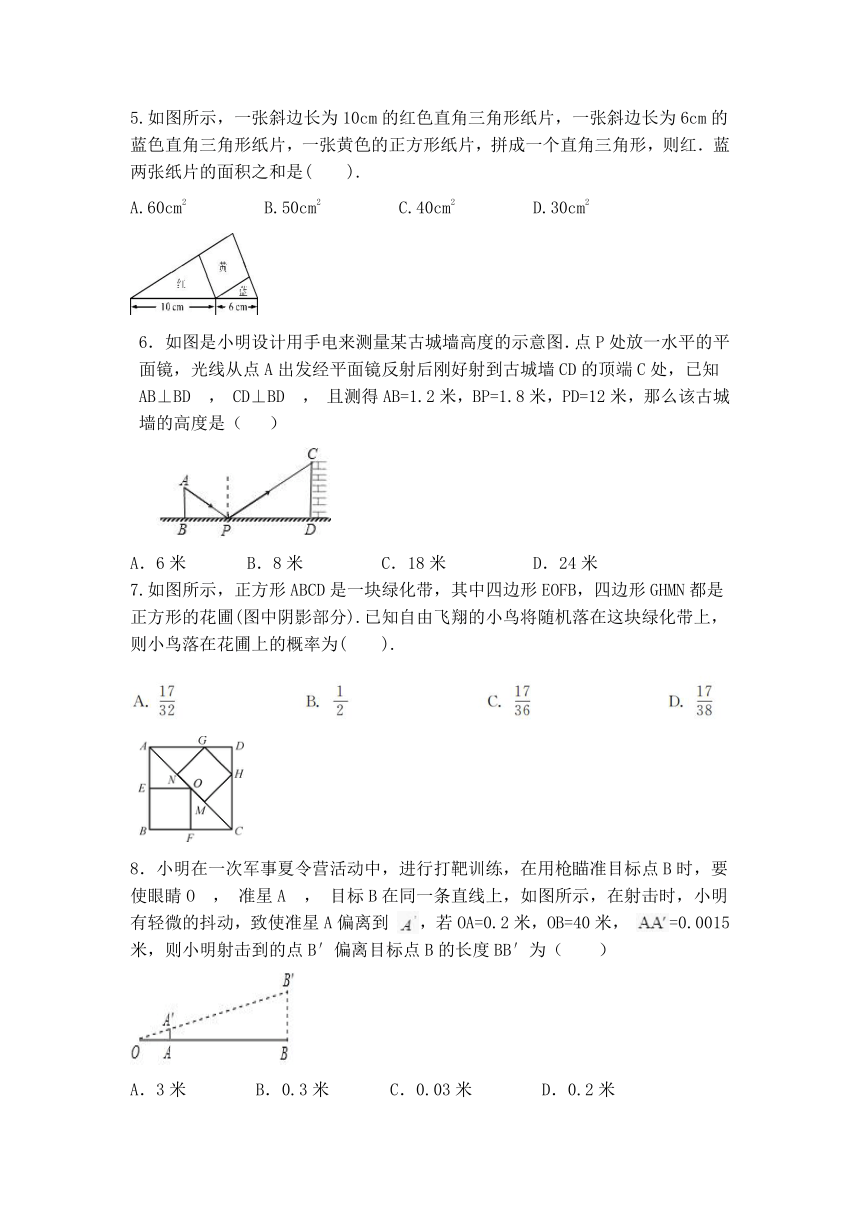
| 格式 | zip | ||
| 文件大小 | 223.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 00:00:00 | ||
图片预览


文档简介
北师大版九年级数学上册第四章4.6利用相似三角形测高
同步测试
一.选择题
1.如图所示,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上.若CD=1.8cm,则AB的长为(
).
A.7.2cm
B.5.4cm
C.3.6cm
D.0.6cm
2.如图,AB是斜靠在墙上的一个梯子,梯脚B距墙1.4m,梯上点D距墙DE=1.2m,BD长0.5m,且△ADE∽△ABC
,
则梯子的长为( )
A.3.5m
B.3.85m
C.4m
D.4.2m
3.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学名著《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为(
).
A.1.25尺
B.57.5尺
C.6.25尺
D.56.5尺
4.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
A.10米
B.12米
C.15米
D.22.5米
5.如图所示,一张斜边长为10cm的红色直角三角形纸片,一张斜边长为6cm的蓝色直角三角形纸片,一张黄色的正方形纸片,拼成一个直角三角形,则红.蓝两张纸片的面积之和是(
).
A.60cm2
B.50cm2
C.40cm2
D.30cm2
如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD
,
CD⊥BD
,
且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是(?
)
A.6米
B.8米
C.18米
D.24米
7.如图所示,正方形ABCD是一块绿化带,其中四边形EOFB,四边形GHMN都是正方形的花圃(图中阴影部分).已知自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为(
).
8.小明在一次军事夏令营活动中,进行打靶训练,在用枪瞄准目标点B时,要使眼睛O
,
准星A
,
目标B在同一条直线上,如图所示,在射击时,小明有轻微的抖动,致使准星A偏离到
,若OA=0.2米,OB=40米,
=0.0015米,则小明射击到的点B′偏离目标点B的长度BB′为( )
A.3米
B.0.3米
C.0.03米
D.0.2米
9.某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5m的标杆DF,如右图,量出DF的影子EF的长度为1m,同一时刻测量旗杆AC的影子BC的长度为6m,那么旗杆AC的高度为( )
A.6m B.7m C.8.5m D.9m
10.已知如图,小明在打网球时,要使球恰好能打过网,而且落在离网5m的位置上,则球拍击球的高度h应为(??
?)
A.2.7m
B.1.8m
C.0.9m
D.2.5m
11.如图,是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.2m,BP=1.8m,PD=12m.那么该古城墙CD的高度是(
)
A.6m B.8m C.18m D.21m
12.如图所示的测量旗杆的方法,已知AB是标杆,BC表示AB在太阳光下的影子,叙述错误的是(??
?)
A.可以利用在同一时刻,不同物体与其影长的比相等来计算旗杆的高
B.只需测量出标杆和旗杆的影长就可计算出旗杆的高
C.可以利用△ABC∽△EDB
,
来计算旗杆的高
D.需要测量出AB.BC和DB的长,才能计算出旗杆的高
二.填空题
13.如右图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为
.
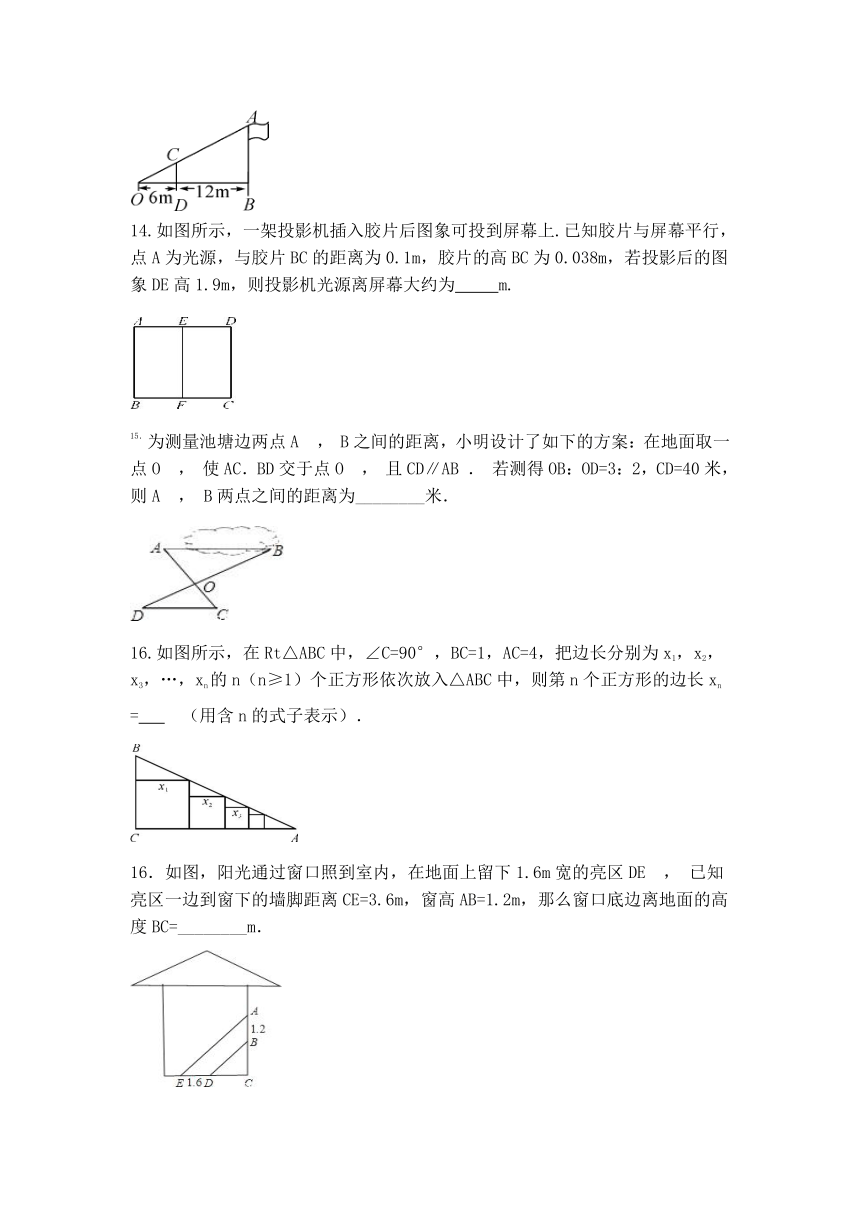
14.如图所示,一架投影机插入胶片后图象可投到屏幕上.已知胶片与屏幕平行,点A为光源,与胶片BC的距离为0.1m,胶片的高BC为0.038m,若投影后的图象DE高1.9m,则投影机光源离屏幕大约为
m.
为测量池塘边两点A
,
B之间的距离,小明设计了如下的方案:在地面取一点O
,
使AC.BD交于点O
,
且CD∥AB
.
若测得OB:OD=3:2,CD=40米,则A
,
B两点之间的距离为________米.
16.如图所示,在Rt△ABC中,∠C=90°,BC=1,AC=4,把边长分别为x1,x2,x3,…,xn的n(n≥1)个正方形依次放入△ABC中,则第n个正方形的边长xn
=
(用含n的式子表示).
如图,阳光通过窗口照到室内,在地面上留下1.6m宽的亮区DE
,
已知亮区一边到窗下的墙脚距离CE=3.6m,窗高AB=1.2m,那么窗口底边离地面的高度BC=________m.
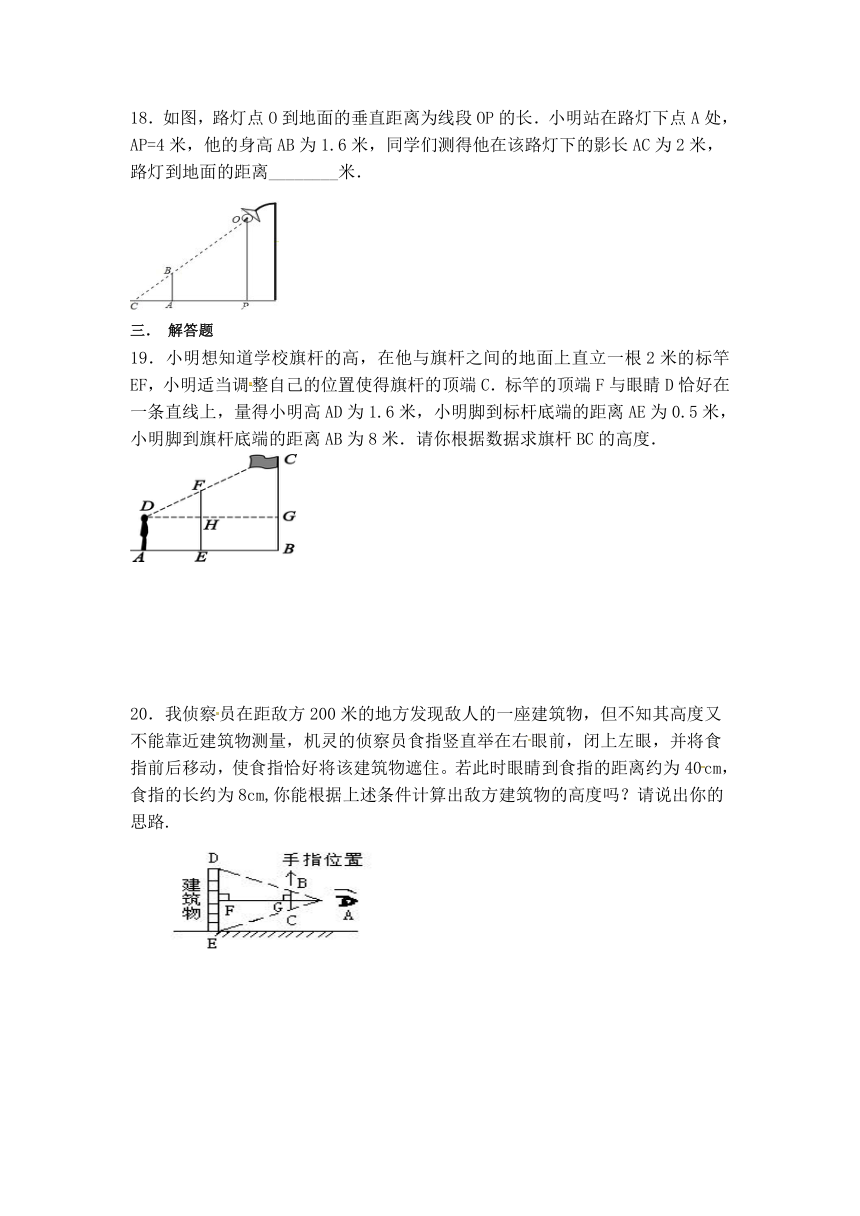
18.如图,路灯点O到地面的垂直距离为线段OP的长.小明站在路灯下点A处,AP=4米,他的身高AB为1.6米,同学们测得他在该路灯下的影长AC为2米,路灯到地面的距离________米.
解答题
19.小明想知道学校旗杆的高,在他与旗杆之间的地面上直立一根2米的标竿EF,小明适当调整自己的位置使得旗杆的顶端C.标竿的顶端F与眼睛D恰好在一条直线上,量得小明高AD为1.6米,小明脚到标杆底端的距离AE为0.5米,小明脚到旗杆底端的距离AB为8米.请你根据数据求旗杆BC的高度.
我侦察员在距敌方200米的地方发现敌人的一座建筑物,但不知其高度又不能靠近建筑物测量,机灵的侦察员食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住。若此时眼睛到食指的距离约为40cm,食指的长约为8cm,你能根据上述条件计算出敌方建筑物的高度吗?请说出你的思路.
21.小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D.B.F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
(1)小明距离路灯多远?
(2)求路灯高度.
22.如图所示,在水平桌面上的两个“E”,当点P1,P2,O在同一条直线上时,在点O处用①号“E”测得的视力与用②号“E”测得的视力相同.
(1)图中b1,b2,l1,l2满足怎样的关系式?
(2)若b1=3.2cm,b2=2cm,①号“E”的测试距离l1=8m,要使测得的视力相同,则②号“E”的测试距离l2应为多少?
23.有一张锐角三角形卡纸余料ABC,它的边BC=120cm,高AD=80cm,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2∶5的矩形纸片EFGH和正方形纸片PMNQ,裁剪时,矩形纸片的较长边在BC上,正方形纸片的一边在矩形纸片的较长边EH上,其余顶点分别在AB,AC上,具体裁剪方式如图所示.
(1)求矩形纸片较长边EH的长.
(2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪的:先沿着剩余余料△AEH中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.
24.如图所示,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以1cm/s的速度分别沿CA,CB向终点A,B移动,同时动点P从点B出发,以2cm/s的速度沿BA向终点A移动,连结PM,PN,设移动时间为t(单位:s,0<t<2.5).
(1)当t为何值时,以点A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
答案提示
B
2.A.
3.B
4.A.
5.D
6.B.
7.C
8.B
9.D
10.A. 11.B
12.B.
13.9m
14.
5
15.60.
16.
17.1.5.
18.4.8米.
19.解:证△DCG∽△DFH,求得CG=6.4米,BC=8米.
20.
解:过A作AG⊥BC于G交DE于F.又BC∥DE,故AF⊥DE,易知⊿ADE∽⊿ABC,
从而故
(1)解:设DB=xm,
∵AB∥CD
,
∴∠QBA=∠QDC
,
∠QAB=∠QCD
,
∴△QAB∽△QCD
∴
同理可得
∵CD=EF
∴
∴
∴x=12
即小明距离路灯12m
.
(2)由
得
∴CD=6
即路灯高6m.
22.【答案】(1)
=.
(2)∵=,b1=3.2(cm),b2=2(cm),l1=8(m),∴=.∴l2=5(m).∴②号“E”的测试距离是l2为5m.
23.【答案】(1)设EF=2x,则EH=5x.∵矩形对边EH∥BC,∴△AEH∽△ABC.∴,解得x=15.∴EH=5x=15×5=75(cm),∴矩形纸片较长边EH的长为75cm.
(2)小聪的剪法不正确.理由如下:设正方形PMNQ的边长为a(cm).∵AR=AD-RD=80-2×15=50(cm),∴AK=(50-a)(m).由题意知△APQ∽△AEH,∴
,解得a=30.与边EH平行的中位线长为×75=37.5(cm).∵37.5≠30,∴小聪的剪法不正确.
24.【答案】∵∠C=90°,AC=4(cm),BC=3(cm),∴AB==5(cm).
(1)以点A,P,M为顶点的三角形与△ABC相似,分两种情况:
①当△AMP∽△ABC时,,解得t=32.
②当△APM∽△ABC时,,解得t=0(不合题意,舍去).
综上所述,当t=s时,以点A,P,M为顶点的三角形与△ABC相似.
(2)存在某一时刻t,使四边形APNC的面积S有最小值.
理由如下:
假设存在某一时刻t,使四边形APNC的面积S有最小值.
如答图所示,过点P作PH⊥BC于点H,则PH∥AC,
∴.
∴S=S△ABC-S△BPN=.
∵>0,∴S有最小值.当t=时,S最小值=.∴当t=s时,四边形APNC的面积S有最小值,其最小值是cm2.
同步测试
一.选择题
1.如图所示,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上.若CD=1.8cm,则AB的长为(
).
A.7.2cm
B.5.4cm
C.3.6cm
D.0.6cm
2.如图,AB是斜靠在墙上的一个梯子,梯脚B距墙1.4m,梯上点D距墙DE=1.2m,BD长0.5m,且△ADE∽△ABC
,
则梯子的长为( )
A.3.5m
B.3.85m
C.4m
D.4.2m
3.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学名著《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为(
).
A.1.25尺
B.57.5尺
C.6.25尺
D.56.5尺
4.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
A.10米
B.12米
C.15米
D.22.5米
5.如图所示,一张斜边长为10cm的红色直角三角形纸片,一张斜边长为6cm的蓝色直角三角形纸片,一张黄色的正方形纸片,拼成一个直角三角形,则红.蓝两张纸片的面积之和是(
).
A.60cm2
B.50cm2
C.40cm2
D.30cm2
如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD
,
CD⊥BD
,
且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是(?
)
A.6米
B.8米
C.18米
D.24米
7.如图所示,正方形ABCD是一块绿化带,其中四边形EOFB,四边形GHMN都是正方形的花圃(图中阴影部分).已知自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为(
).
8.小明在一次军事夏令营活动中,进行打靶训练,在用枪瞄准目标点B时,要使眼睛O
,
准星A
,
目标B在同一条直线上,如图所示,在射击时,小明有轻微的抖动,致使准星A偏离到
,若OA=0.2米,OB=40米,
=0.0015米,则小明射击到的点B′偏离目标点B的长度BB′为( )
A.3米
B.0.3米
C.0.03米
D.0.2米
9.某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5m的标杆DF,如右图,量出DF的影子EF的长度为1m,同一时刻测量旗杆AC的影子BC的长度为6m,那么旗杆AC的高度为( )
A.6m B.7m C.8.5m D.9m
10.已知如图,小明在打网球时,要使球恰好能打过网,而且落在离网5m的位置上,则球拍击球的高度h应为(??
?)
A.2.7m
B.1.8m
C.0.9m
D.2.5m
11.如图,是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD.且测得AB=1.2m,BP=1.8m,PD=12m.那么该古城墙CD的高度是(
)
A.6m B.8m C.18m D.21m
12.如图所示的测量旗杆的方法,已知AB是标杆,BC表示AB在太阳光下的影子,叙述错误的是(??
?)
A.可以利用在同一时刻,不同物体与其影长的比相等来计算旗杆的高
B.只需测量出标杆和旗杆的影长就可计算出旗杆的高
C.可以利用△ABC∽△EDB
,
来计算旗杆的高
D.需要测量出AB.BC和DB的长,才能计算出旗杆的高
二.填空题
13.如右图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为
.
14.如图所示,一架投影机插入胶片后图象可投到屏幕上.已知胶片与屏幕平行,点A为光源,与胶片BC的距离为0.1m,胶片的高BC为0.038m,若投影后的图象DE高1.9m,则投影机光源离屏幕大约为
m.
为测量池塘边两点A
,
B之间的距离,小明设计了如下的方案:在地面取一点O
,
使AC.BD交于点O
,
且CD∥AB
.
若测得OB:OD=3:2,CD=40米,则A
,
B两点之间的距离为________米.
16.如图所示,在Rt△ABC中,∠C=90°,BC=1,AC=4,把边长分别为x1,x2,x3,…,xn的n(n≥1)个正方形依次放入△ABC中,则第n个正方形的边长xn
=
(用含n的式子表示).
如图,阳光通过窗口照到室内,在地面上留下1.6m宽的亮区DE
,
已知亮区一边到窗下的墙脚距离CE=3.6m,窗高AB=1.2m,那么窗口底边离地面的高度BC=________m.
18.如图,路灯点O到地面的垂直距离为线段OP的长.小明站在路灯下点A处,AP=4米,他的身高AB为1.6米,同学们测得他在该路灯下的影长AC为2米,路灯到地面的距离________米.
解答题
19.小明想知道学校旗杆的高,在他与旗杆之间的地面上直立一根2米的标竿EF,小明适当调整自己的位置使得旗杆的顶端C.标竿的顶端F与眼睛D恰好在一条直线上,量得小明高AD为1.6米,小明脚到标杆底端的距离AE为0.5米,小明脚到旗杆底端的距离AB为8米.请你根据数据求旗杆BC的高度.
我侦察员在距敌方200米的地方发现敌人的一座建筑物,但不知其高度又不能靠近建筑物测量,机灵的侦察员食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住。若此时眼睛到食指的距离约为40cm,食指的长约为8cm,你能根据上述条件计算出敌方建筑物的高度吗?请说出你的思路.
21.小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D.B.F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
(1)小明距离路灯多远?
(2)求路灯高度.
22.如图所示,在水平桌面上的两个“E”,当点P1,P2,O在同一条直线上时,在点O处用①号“E”测得的视力与用②号“E”测得的视力相同.
(1)图中b1,b2,l1,l2满足怎样的关系式?
(2)若b1=3.2cm,b2=2cm,①号“E”的测试距离l1=8m,要使测得的视力相同,则②号“E”的测试距离l2应为多少?
23.有一张锐角三角形卡纸余料ABC,它的边BC=120cm,高AD=80cm,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2∶5的矩形纸片EFGH和正方形纸片PMNQ,裁剪时,矩形纸片的较长边在BC上,正方形纸片的一边在矩形纸片的较长边EH上,其余顶点分别在AB,AC上,具体裁剪方式如图所示.
(1)求矩形纸片较长边EH的长.
(2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪的:先沿着剩余余料△AEH中与边EH平行的中位线剪一刀,再沿过该中位线两端点向边EH所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.
24.如图所示,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以1cm/s的速度分别沿CA,CB向终点A,B移动,同时动点P从点B出发,以2cm/s的速度沿BA向终点A移动,连结PM,PN,设移动时间为t(单位:s,0<t<2.5).
(1)当t为何值时,以点A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
答案提示
B
2.A.
3.B
4.A.
5.D
6.B.
7.C
8.B
9.D
10.A. 11.B
12.B.
13.9m
14.
5
15.60.
16.
17.1.5.
18.4.8米.
19.解:证△DCG∽△DFH,求得CG=6.4米,BC=8米.
20.
解:过A作AG⊥BC于G交DE于F.又BC∥DE,故AF⊥DE,易知⊿ADE∽⊿ABC,
从而故
(1)解:设DB=xm,
∵AB∥CD
,
∴∠QBA=∠QDC
,
∠QAB=∠QCD
,
∴△QAB∽△QCD
∴
同理可得
∵CD=EF
∴
∴
∴x=12
即小明距离路灯12m
.
(2)由
得
∴CD=6
即路灯高6m.
22.【答案】(1)
=.
(2)∵=,b1=3.2(cm),b2=2(cm),l1=8(m),∴=.∴l2=5(m).∴②号“E”的测试距离是l2为5m.
23.【答案】(1)设EF=2x,则EH=5x.∵矩形对边EH∥BC,∴△AEH∽△ABC.∴,解得x=15.∴EH=5x=15×5=75(cm),∴矩形纸片较长边EH的长为75cm.
(2)小聪的剪法不正确.理由如下:设正方形PMNQ的边长为a(cm).∵AR=AD-RD=80-2×15=50(cm),∴AK=(50-a)(m).由题意知△APQ∽△AEH,∴
,解得a=30.与边EH平行的中位线长为×75=37.5(cm).∵37.5≠30,∴小聪的剪法不正确.
24.【答案】∵∠C=90°,AC=4(cm),BC=3(cm),∴AB==5(cm).
(1)以点A,P,M为顶点的三角形与△ABC相似,分两种情况:
①当△AMP∽△ABC时,,解得t=32.
②当△APM∽△ABC时,,解得t=0(不合题意,舍去).
综上所述,当t=s时,以点A,P,M为顶点的三角形与△ABC相似.
(2)存在某一时刻t,使四边形APNC的面积S有最小值.
理由如下:
假设存在某一时刻t,使四边形APNC的面积S有最小值.
如答图所示,过点P作PH⊥BC于点H,则PH∥AC,
∴.
∴S=S△ABC-S△BPN=.
∵>0,∴S有最小值.当t=时,S最小值=.∴当t=s时,四边形APNC的面积S有最小值,其最小值是cm2.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
