人教版八年级数学上册教学课件:14.1.4 整式的乘法(16张)
文档属性
| 名称 | 人教版八年级数学上册教学课件:14.1.4 整式的乘法(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 413.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-21 15:58:06 | ||
图片预览





文档简介
(共16张PPT)
整式的乘除与因式分解
14.1.4
多项式与多项式相乘
目录
1.几个单项式的和叫做多项式
2.在多项式中,每个单项式叫做多项式的项。
注意:
多项式的每一项都要带上单项式的符号
新课导入
知识回顾
比如:
学习目标
1.了解并掌握多项式与多项式相乘的运算法则.(重点)
2.掌握多项式与多项式相乘的运算法则的推导.(难点)
新课导入
如图把一块原长a
m、
宽p
m的长方形绿地,加长了
b
m,加宽了qm.
你能用几种方法求出扩大后的绿地面积?
a
p
q
b
不同的表示方法:
(a+b)(p+q);
a(
p+q)+b
(p+q);
p(a+b)+q(a+b);
ap+aq+bp+bq.
由于四种方法表示同一个数量,所以(a+b)(p+q)=
ap+aq+bp+bq上面的等式提供了多项式与多项式相乘的方法.
新课讲解
知识讲解
探究
多项式乘多项式法则
法则:一般地,多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
式子表示:(a+b)(p+q)=ap+aq+bp+bq(a,b,p,q分别是单项式).
重
点
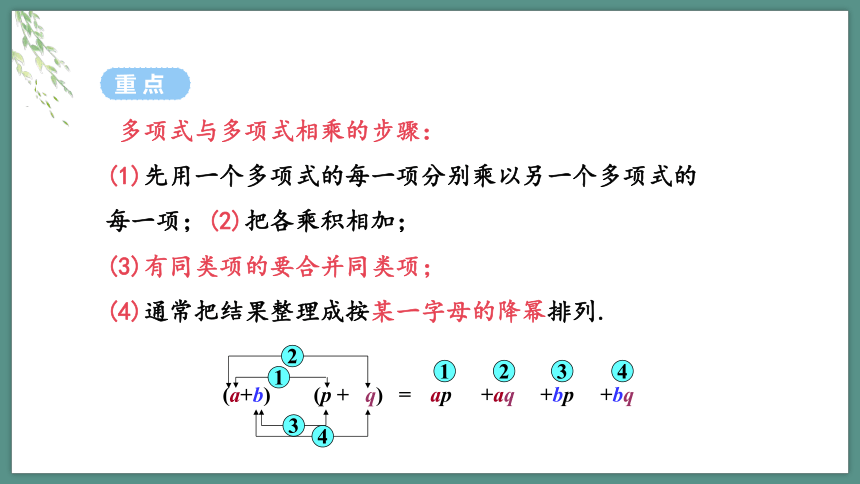
多项式与多项式相乘的步骤:
(1)先用一个多项式的每一项分别乘以另一个多项式的每一项;(2)把各乘积相加;
(3)有同类项的要合并同类项;
(4)通常把结果整理成按某一字母的降幂排列.
(a+b)
(p
+
q)
1
=
1
ap
2
2
+aq
3
3
+bp
4
4
+bq
重
点
(1)多项式乘法法则的实质是将多项式与多项式相乘转化为几个单项式相乘的和的形式;
(2)
多项式与多项式相乘的结果仍为多项式,若有同类项,一定要及时合并同类项,在合并同类项之前,积的项数应该是两个多项式的项数之积;
(3)多项式乘法法则也适用于多个多项式相乘,即按顺序先将前两个多项式相乘,再把乘积与第三个多项式相乘,以此类推.
课堂练习
练一练
1
计算:
(1)
(3a+1)(a-2)
;
解:(1)
(3a+1)(a-2)
=
3a?a+3a?(-2)+1?a+
1?(-2)
=
3a2-6a+a-2
=
3a2-5a-2
;
(2)
(1-x+y)(-x-y)
=-x-y+x2+xy-xy-y2
=-x-y+x2-y2
.
(2)
(1-x+y)(-x-y).
课堂练习
练一练
2
计算:(1)
(4a-b)(-2b)2
;
解:(1)
(4a-b)(-2b)2
=
(4a-b)?4b2
=
4a?4b2+(-b)?4b2
=
16ab2-4b3
;
(2)
课堂练习
先化简,再求值:(x+2)(x-2)+x(1-x),其中x=-1.
(x+2)(x-2)+x(1-x)
=
x2-2x+2x-4+x-x2
=
x-4.
因为当x=-1,所以原式=-5.
解:
课堂练习
2.已知M,N分别是2次多项式和3次多项式,则M×N( )
A.一定是5次多项式
B.一定是6次多项式
C.一定是不高于5次的多项式
D.无法确定积的次数
分析:最高次数+最高次数=最终多项式次数。即2+3=5
A
课堂练习
先化简,再求值:(x-2y)(x+3y)-(2x-y)(x-4y),其中x=-1,y=2.
解:
原式=x2+3xy-2xy-6y2-(2x2-8xy-xy+4y2)
=x2+xy-6y2-(2x2-9xy+4y2)
=x2+xy-6y2-2x2+9xy-4y2
=-x2+10xy-10y2.
当x=-1,y=2时,
原式=-(-1)2+10×(-1)×2-10×22
=-1-20-40
=-61.
课堂小结
多项式乘多项式
1.运算法则:先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多项式与多项式相乘易犯错误:
1.漏项
2.丢符号
3.最后含有同类项
必做题:课本的对应习题
作业:
感谢各位观看
整式的乘除与因式分解
14.1.4
多项式与多项式相乘
目录
1.几个单项式的和叫做多项式
2.在多项式中,每个单项式叫做多项式的项。
注意:
多项式的每一项都要带上单项式的符号
新课导入
知识回顾
比如:
学习目标
1.了解并掌握多项式与多项式相乘的运算法则.(重点)
2.掌握多项式与多项式相乘的运算法则的推导.(难点)
新课导入
如图把一块原长a
m、
宽p
m的长方形绿地,加长了
b
m,加宽了qm.
你能用几种方法求出扩大后的绿地面积?
a
p
q
b
不同的表示方法:
(a+b)(p+q);
a(
p+q)+b
(p+q);
p(a+b)+q(a+b);
ap+aq+bp+bq.
由于四种方法表示同一个数量,所以(a+b)(p+q)=
ap+aq+bp+bq上面的等式提供了多项式与多项式相乘的方法.
新课讲解
知识讲解
探究
多项式乘多项式法则
法则:一般地,多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
式子表示:(a+b)(p+q)=ap+aq+bp+bq(a,b,p,q分别是单项式).
重
点
多项式与多项式相乘的步骤:
(1)先用一个多项式的每一项分别乘以另一个多项式的每一项;(2)把各乘积相加;
(3)有同类项的要合并同类项;
(4)通常把结果整理成按某一字母的降幂排列.
(a+b)
(p
+
q)
1
=
1
ap
2
2
+aq
3
3
+bp
4
4
+bq
重
点
(1)多项式乘法法则的实质是将多项式与多项式相乘转化为几个单项式相乘的和的形式;
(2)
多项式与多项式相乘的结果仍为多项式,若有同类项,一定要及时合并同类项,在合并同类项之前,积的项数应该是两个多项式的项数之积;
(3)多项式乘法法则也适用于多个多项式相乘,即按顺序先将前两个多项式相乘,再把乘积与第三个多项式相乘,以此类推.
课堂练习
练一练
1
计算:
(1)
(3a+1)(a-2)
;
解:(1)
(3a+1)(a-2)
=
3a?a+3a?(-2)+1?a+
1?(-2)
=
3a2-6a+a-2
=
3a2-5a-2
;
(2)
(1-x+y)(-x-y)
=-x-y+x2+xy-xy-y2
=-x-y+x2-y2
.
(2)
(1-x+y)(-x-y).
课堂练习
练一练
2
计算:(1)
(4a-b)(-2b)2
;
解:(1)
(4a-b)(-2b)2
=
(4a-b)?4b2
=
4a?4b2+(-b)?4b2
=
16ab2-4b3
;
(2)
课堂练习
先化简,再求值:(x+2)(x-2)+x(1-x),其中x=-1.
(x+2)(x-2)+x(1-x)
=
x2-2x+2x-4+x-x2
=
x-4.
因为当x=-1,所以原式=-5.
解:
课堂练习
2.已知M,N分别是2次多项式和3次多项式,则M×N( )
A.一定是5次多项式
B.一定是6次多项式
C.一定是不高于5次的多项式
D.无法确定积的次数
分析:最高次数+最高次数=最终多项式次数。即2+3=5
A
课堂练习
先化简,再求值:(x-2y)(x+3y)-(2x-y)(x-4y),其中x=-1,y=2.
解:
原式=x2+3xy-2xy-6y2-(2x2-8xy-xy+4y2)
=x2+xy-6y2-(2x2-9xy+4y2)
=x2+xy-6y2-2x2+9xy-4y2
=-x2+10xy-10y2.
当x=-1,y=2时,
原式=-(-1)2+10×(-1)×2-10×22
=-1-20-40
=-61.
课堂小结
多项式乘多项式
1.运算法则:先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
多项式与多项式相乘易犯错误:
1.漏项
2.丢符号
3.最后含有同类项
必做题:课本的对应习题
作业:
感谢各位观看
