人教版版九年级上册24.2.2 圆的切线的性质和判定定理课件(29张)
文档属性
| 名称 | 人教版版九年级上册24.2.2 圆的切线的性质和判定定理课件(29张) |  | |
| 格式 | zip | ||
| 文件大小 | 387.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-21 15:59:22 | ||
图片预览

文档简介
(共29张PPT)
分享
一切优秀的品质都源于自制,不管是勤奋还是奋进,都必须以自制为前提,奋进必为落后所占据。只有管得住自己的人,才能管得住别人,管好别人的人不一定管好自己。但管得住自己的人一定能管好别人。世界上的名臣良将都是首先从自己做起,做三军之表才能服人,希望同学们加强自制力,万事首先从自己想起,管住心灵的羁荡,才能管住苍穹。
24.2.2
圆的切线的性质和判定定理
.O
B
A
O
r
M
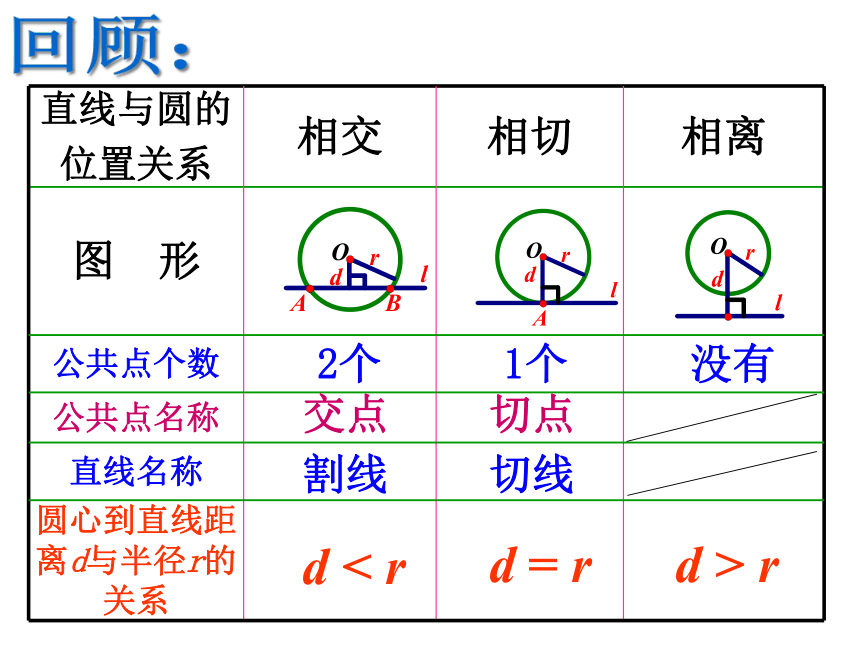
直线与圆的
位置关系
相交
相切
相离
图
形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2个
交点
割线
1个
切点
切线
d
<
r
d
=
r
d
>
r
没有
回顾:
本节专门讨论直线与圆相切的情形.
.O
相交
相切
相离
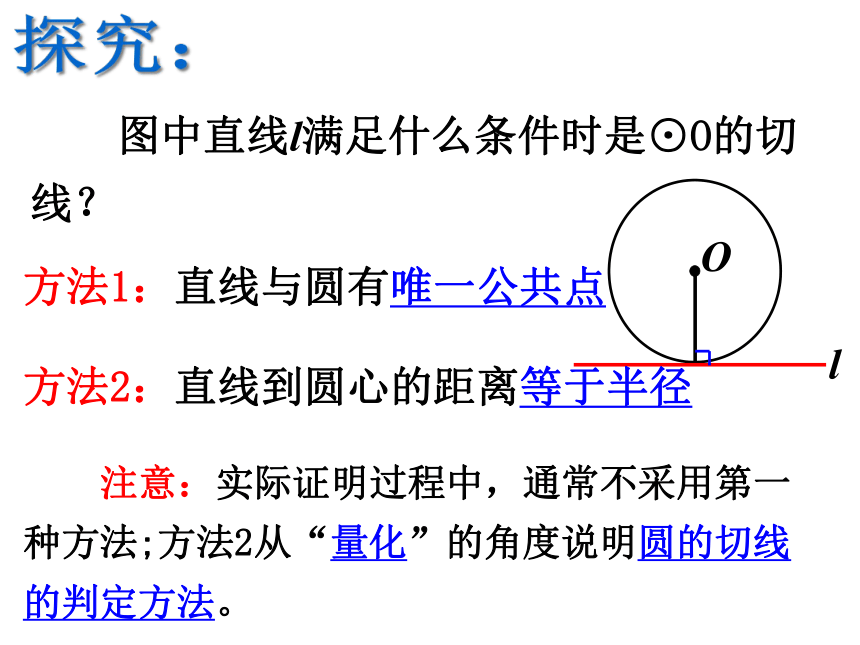
图中直线l满足什么条件时是⊙O的切线?
探究:
O
l
方法1:直线与圆有唯一公共点
方法2:直线到圆心的距离等于半径
注意:实际证明过程中,通常不采用第一种方法;方法2从“量化”的角度说明圆的切线的判定方法。
(1)
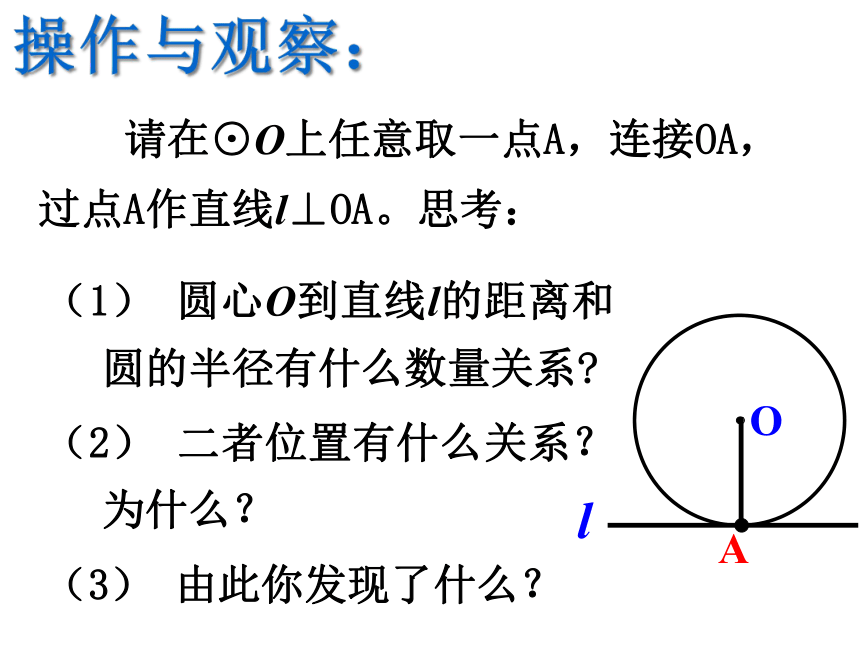
圆心O到直线l的距离和圆的半径有什么数量关系?
(2)
二者位置有什么关系?为什么?
(3)
由此你发现了什么?
O
请在⊙O上任意取一点A,连接OA,过点A作直线l⊥OA。思考:
l
A
操作与观察:
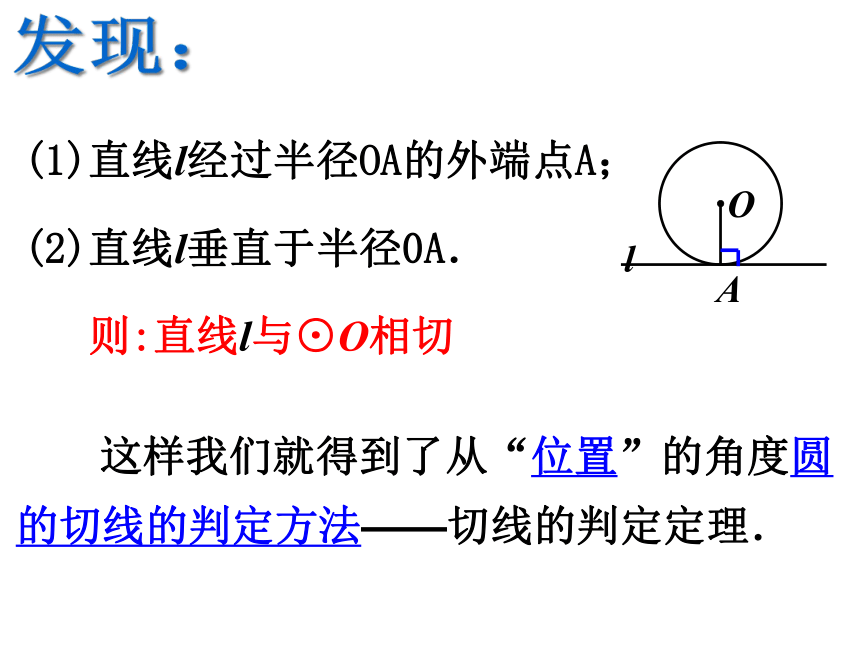
(1)直线l经过半径OA的外端点A;
(2)直线l垂直于半径0A.
则:直线l与⊙O相切
这样我们就得到了从“位置”的角度圆的切线的判定方法——切线的判定定理.
A
O
l
发现:
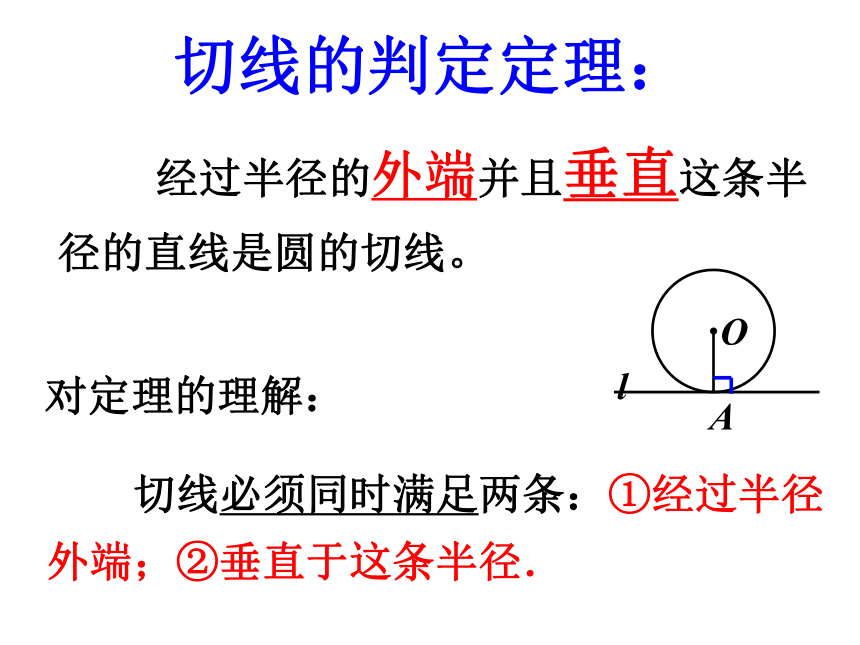
切线的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线。
对定理的理解:
切线必须同时满足两条:①经过半径外端;②垂直于这条半径.
A
O
l
O
r
l
A
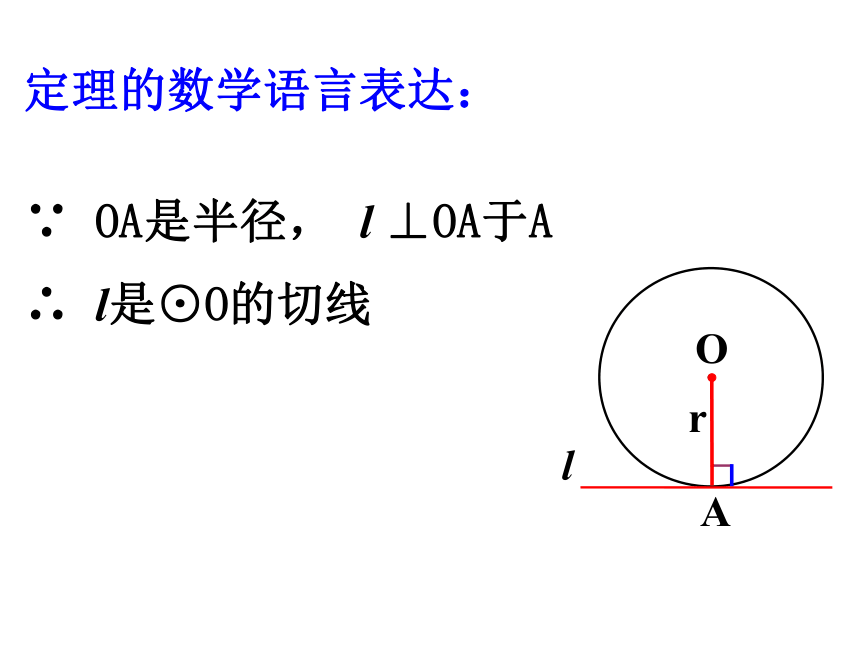
∵
OA是半径,
l
⊥OA于A
∴
l是⊙O的切线
定理的数学语言表达:
判断:
(1)过半径的外端的直线是圆的切线(
)
(2)与半径垂直的的直线是圆的切线(
)
(3)过半径的端点与半径垂直的直线是圆的切线(
)
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
巩固:
两个条件缺一不可
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线.
判定直线与圆相切有哪些方法?
归纳:
例1
如图,已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可。
例题:
有交点,连半径,证垂直
〖规范板书〗
已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
证明:连结OC(如图)。
∵
OA=OB,CA=CB,
∴
AB⊥OC(三线合一)
∵
OC是⊙O的半径
∴
AB是⊙O的切线。
例2
如图,已知:O为∠BAC平分线上一
点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。
求证:⊙O与AC相切。
O
A
B
C
E
D
无交点,作垂直,证半径
〖规范板书〗
已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。
O
A
B
C
E
D
证明:过O作OE⊥AC于E。
∵
AO平分∠BAC,
OD⊥AB于点D
∴
OE=OD
∵
OD是⊙O的半径
∴
OE也是半径
∴
AC是⊙O的切线。
O
B
A
C
O
A
B
C
E
D
归纳:
例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直.简记为:有交点,连半径,证垂直.
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段,再证垂线段长等于半径长.简记为:无交点,作垂直,证半径.
.
O
A
L
思考?如图:如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢?
一定垂直
切线的性质定理:
圆的切线垂直于过切点的半径
符号语言:∵
l是⊙O的切线,切点为A
∴
l
⊥OA
O
M
反证法
这与“直线l是圆O的切线”矛盾.
切线的性质定理:
圆的切线垂直于经过切点的半径
证明:假设l与OA不垂直,
作OM⊥
l于M
因“垂线段最短”,
故OA>OM,
即圆心到直线的距离小于半径.
A
故直线l与圆O一定垂直.
【切线的性质定理】
切线的性质定理:圆的切线垂直于过切点的半径。
O
A
l
因为经过一点只有一条直线与已知直线垂直,所以经过圆心垂直于切线的直线一定过切点;反之,过切点且垂直于切线的直线也一定过圆心.由此得到:
1
切线的性质定理:圆的切线垂直于经过切点的半径.
切线的性质定理的推论1:经过圆心且垂直于切线的直线必经过切点.
切线的性质定理的推论2:经过切点且垂直于切线的直线必经过圆心.
O.
A
1、切线和圆只有一个公共点。
2、切线和圆心的距离等于半径。
3、切线垂直于过切点的半径。
4、经过圆心垂直于切线的直线必过切点。
5、经过切点垂直于切线的直线必过圆心。
判断:
切线的性质定理:圆的切线垂直于过切点的半径。
归纳:
O
A
l
①过半径外端;
②垂直于这条半径.
切线
①圆的切线;
②过切点的半径.
切线垂直于半径
切线判定定理:
切线性质定理:
比较:
O
A
l
1、如图,
⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少?
例题
注:已知切线、切点,则连接半径,应用切线的性质定理得到垂直关系,从而应用勾股定理计算。
2、如图.
AB为⊙O的直径,C为⊙O上一点,AD和
过C点的切线互相垂直,垂足为
D,求证:AC平分∠DAB.
A
B
O
C
D
证明:连接OC,
∴OC⊥CD.
又∵AD⊥CD,
∴OC//AD.
∵OC=OA.
∴
∠CAO=∠ACO.
∴
∠CAD=∠CAO.
故AC平分∠DAB.
∵CD是⊙O的切线,
由此得
∠ACO=∠CAD.
①过半径外端;
②垂直于这条半径.
切线
①圆的切线;
②过切点的半径.
切线垂直于半径
切线判定定理:
切线性质定理:
小结:
O
A
l
1.
判定一条直线是圆的切线的三种方法:
直线l
与圆有唯一公共点
与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
l是圆的切线
2.
常用的添辅助线方法?
⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这条垂线段等于圆的半径。(作垂直,证半径)
l是圆的切线
l是圆的切线
课堂小结:
课堂小结:
1、知识:切线的判定定理.着重分析了定理成立的条件,在应用定理时,注重两个条件缺一不可.
2、判定一条直线是圆的切线的三种方法说明:其中(2)和(3)本质相同,只是表达形式不同.解题时,灵活选用其中之一.
如图,AB、AC分别切⊙O于B、C,若∠A=600,点P是圆上异于B、C的一动点,则∠BPC的度数是(
)
A、600
B、1200
C、600或1200
D、1400或600
B
P
C
A
O
分享
一切优秀的品质都源于自制,不管是勤奋还是奋进,都必须以自制为前提,奋进必为落后所占据。只有管得住自己的人,才能管得住别人,管好别人的人不一定管好自己。但管得住自己的人一定能管好别人。世界上的名臣良将都是首先从自己做起,做三军之表才能服人,希望同学们加强自制力,万事首先从自己想起,管住心灵的羁荡,才能管住苍穹。
24.2.2
圆的切线的性质和判定定理
.O
B
A
O
r
M
直线与圆的
位置关系
相交
相切
相离
图
形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
2个
交点
割线
1个
切点
切线
d
<
r
d
=
r
d
>
r
没有
回顾:
本节专门讨论直线与圆相切的情形.
.O
相交
相切
相离
图中直线l满足什么条件时是⊙O的切线?
探究:
O
l
方法1:直线与圆有唯一公共点
方法2:直线到圆心的距离等于半径
注意:实际证明过程中,通常不采用第一种方法;方法2从“量化”的角度说明圆的切线的判定方法。
(1)
圆心O到直线l的距离和圆的半径有什么数量关系?
(2)
二者位置有什么关系?为什么?
(3)
由此你发现了什么?
O
请在⊙O上任意取一点A,连接OA,过点A作直线l⊥OA。思考:
l
A
操作与观察:
(1)直线l经过半径OA的外端点A;
(2)直线l垂直于半径0A.
则:直线l与⊙O相切
这样我们就得到了从“位置”的角度圆的切线的判定方法——切线的判定定理.
A
O
l
发现:
切线的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线。
对定理的理解:
切线必须同时满足两条:①经过半径外端;②垂直于这条半径.
A
O
l
O
r
l
A
∵
OA是半径,
l
⊥OA于A
∴
l是⊙O的切线
定理的数学语言表达:
判断:
(1)过半径的外端的直线是圆的切线(
)
(2)与半径垂直的的直线是圆的切线(
)
(3)过半径的端点与半径垂直的直线是圆的切线(
)
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
巩固:
两个条件缺一不可
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线.
判定直线与圆相切有哪些方法?
归纳:
例1
如图,已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可。
例题:
有交点,连半径,证垂直
〖规范板书〗
已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
证明:连结OC(如图)。
∵
OA=OB,CA=CB,
∴
AB⊥OC(三线合一)
∵
OC是⊙O的半径
∴
AB是⊙O的切线。
例2
如图,已知:O为∠BAC平分线上一
点,OD⊥AB于D,以O为圆心,OD为半径作⊙O。
求证:⊙O与AC相切。
O
A
B
C
E
D
无交点,作垂直,证半径
〖规范板书〗
已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。
O
A
B
C
E
D
证明:过O作OE⊥AC于E。
∵
AO平分∠BAC,
OD⊥AB于点D
∴
OE=OD
∵
OD是⊙O的半径
∴
OE也是半径
∴
AC是⊙O的切线。
O
B
A
C
O
A
B
C
E
D
归纳:
例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直.简记为:有交点,连半径,证垂直.
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段,再证垂线段长等于半径长.简记为:无交点,作垂直,证半径.
.
O
A
L
思考?如图:如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢?
一定垂直
切线的性质定理:
圆的切线垂直于过切点的半径
符号语言:∵
l是⊙O的切线,切点为A
∴
l
⊥OA
O
M
反证法
这与“直线l是圆O的切线”矛盾.
切线的性质定理:
圆的切线垂直于经过切点的半径
证明:假设l与OA不垂直,
作OM⊥
l于M
因“垂线段最短”,
故OA>OM,
即圆心到直线的距离小于半径.
A
故直线l与圆O一定垂直.
【切线的性质定理】
切线的性质定理:圆的切线垂直于过切点的半径。
O
A
l
因为经过一点只有一条直线与已知直线垂直,所以经过圆心垂直于切线的直线一定过切点;反之,过切点且垂直于切线的直线也一定过圆心.由此得到:
1
切线的性质定理:圆的切线垂直于经过切点的半径.
切线的性质定理的推论1:经过圆心且垂直于切线的直线必经过切点.
切线的性质定理的推论2:经过切点且垂直于切线的直线必经过圆心.
O.
A
1、切线和圆只有一个公共点。
2、切线和圆心的距离等于半径。
3、切线垂直于过切点的半径。
4、经过圆心垂直于切线的直线必过切点。
5、经过切点垂直于切线的直线必过圆心。
判断:
切线的性质定理:圆的切线垂直于过切点的半径。
归纳:
O
A
l
①过半径外端;
②垂直于这条半径.
切线
①圆的切线;
②过切点的半径.
切线垂直于半径
切线判定定理:
切线性质定理:
比较:
O
A
l
1、如图,
⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少?
例题
注:已知切线、切点,则连接半径,应用切线的性质定理得到垂直关系,从而应用勾股定理计算。
2、如图.
AB为⊙O的直径,C为⊙O上一点,AD和
过C点的切线互相垂直,垂足为
D,求证:AC平分∠DAB.
A
B
O
C
D
证明:连接OC,
∴OC⊥CD.
又∵AD⊥CD,
∴OC//AD.
∵OC=OA.
∴
∠CAO=∠ACO.
∴
∠CAD=∠CAO.
故AC平分∠DAB.
∵CD是⊙O的切线,
由此得
∠ACO=∠CAD.
①过半径外端;
②垂直于这条半径.
切线
①圆的切线;
②过切点的半径.
切线垂直于半径
切线判定定理:
切线性质定理:
小结:
O
A
l
1.
判定一条直线是圆的切线的三种方法:
直线l
与圆有唯一公共点
与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
l是圆的切线
2.
常用的添辅助线方法?
⑴直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这条垂线段等于圆的半径。(作垂直,证半径)
l是圆的切线
l是圆的切线
课堂小结:
课堂小结:
1、知识:切线的判定定理.着重分析了定理成立的条件,在应用定理时,注重两个条件缺一不可.
2、判定一条直线是圆的切线的三种方法说明:其中(2)和(3)本质相同,只是表达形式不同.解题时,灵活选用其中之一.
如图,AB、AC分别切⊙O于B、C,若∠A=600,点P是圆上异于B、C的一动点,则∠BPC的度数是(
)
A、600
B、1200
C、600或1200
D、1400或600
B
P
C
A
O
同课章节目录
