5.2.3 平行线的性质 课件(共18张PPT)
文档属性
| 名称 | 5.2.3 平行线的性质 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
3.平
行
线
的
性
质
华东师大版
七年级数学上册
教学课件
5.2
平形线
【基本目标】
1.探索平行线的性质,并掌握它们的文字语言、符号语言和图形语言;
2.会用平行线的性质进行简单的计算和推理,结合平行线对图形进行简单的平移.
【学习重点】
掌握平行线的性质.
【学习难点】
平行线的性质的应用.
学习目标
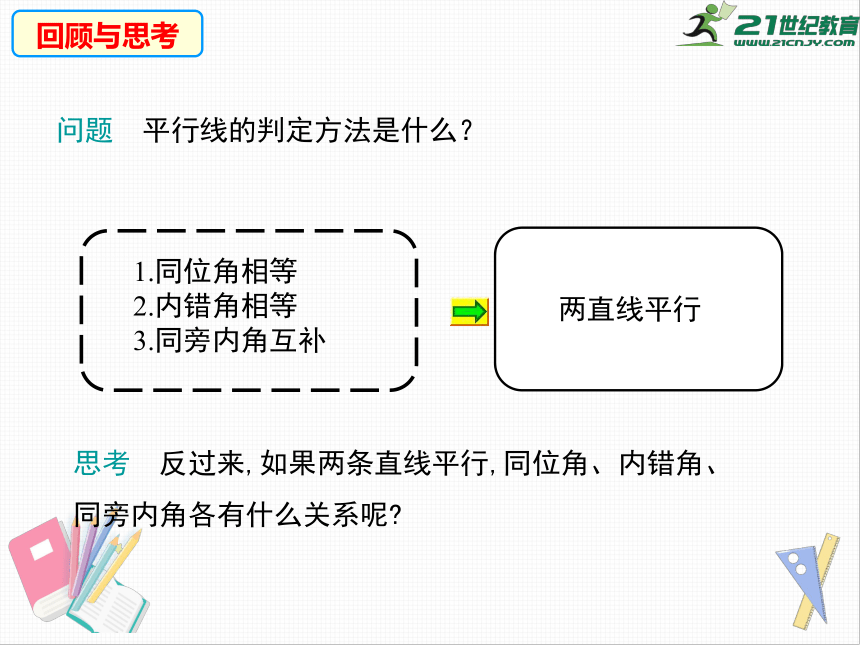
回顾与思考
问题
平行线的判定方法是什么?
1.同位角相等
2.内错角相等
3.同旁内角互补
两直线平行
思考
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
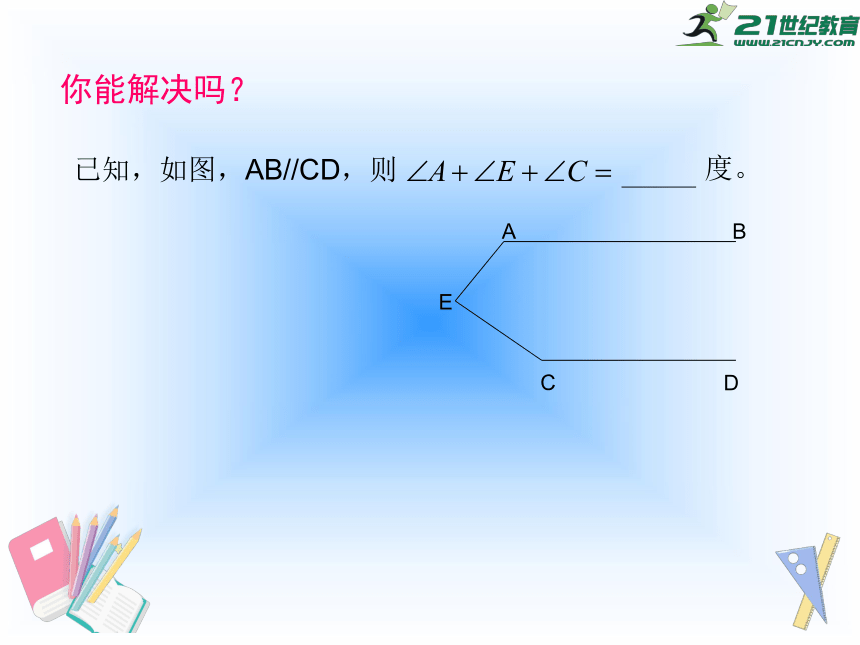
你能解决吗?
已知,如图,AB//CD,则
度。
A
B
C
D
E
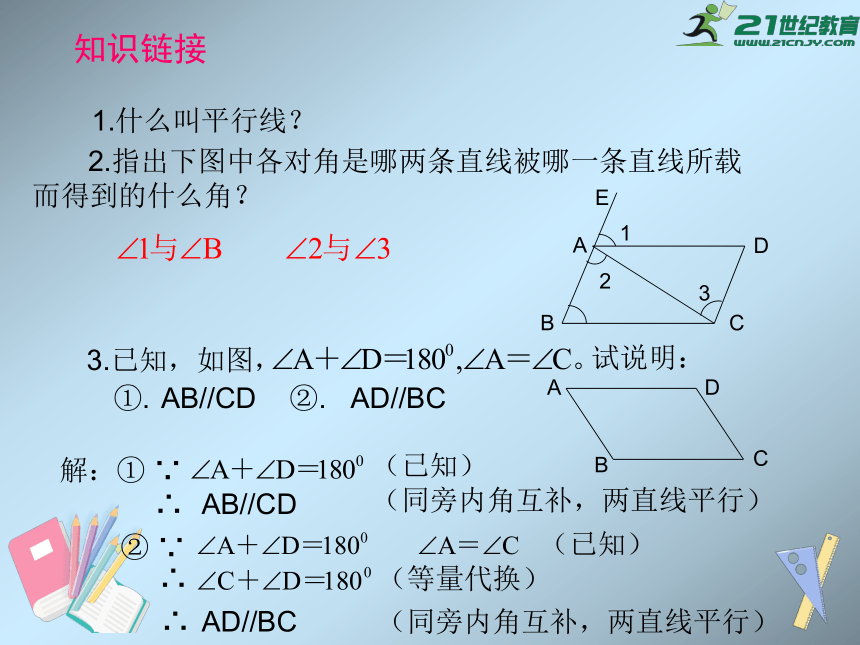
知识链接
1.什么叫平行线?
2.指出下图中各对角是哪两条直线被哪一条直线所载
而得到的什么角?
E
A
B
C
D
1
2
3
3.已知,如图,
试说明:
①.
②.
AB//CD
AD//BC
A
B
C
D
解:①
∵
∴
AB//CD
(已知)
(同旁内角互补,两直线平行)
②
∵
∴
(已知)
(等量代换)
∴
AD//BC
(同旁内角互补,两直线平行)
知识积累
1.用前面学过的画平行线的方法
画两条平行线:
a∥b
2.用第三条直线
l
去截这两条平行线,找找其中的同位角、内错角和同旁内角,猜一猜它们的数量关系,并用量角器去测量验证。
3.归纳你得到的结论:
(1)两直线平行,同位角相等
(2)两直线平行,内错角相等,
(3)两直线平行,同旁内角互补,
∵
a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
知识积累
4.概括平行线的性质:
(1).
两直线平行,同位角相等。
(2).
两直线平行,内错角相等。
(3).
两直线平行,同旁内角互补。
5.理解,记忆
(1).区别异同。
(2).与平行线的判定区别。
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行。
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。
平行线的判定
平行线的性质
对
比
1.判断下列说法是否正确。
(1).
对顶角相等。(
)
(2).
相等的角是对顶角。(
)
(3).
两条直线被第三条直线所截,同位角相等。(
)
(4).
如果直线a、b被c所截得的8个角都相等,则a∥b,c⊥a,c⊥b。(
)
√
×
×
√
2.在下列解答中,填上适当的理由。
(1).
∵AD//BC
(已知)
∴∠B=∠1
(
)
1
A
B
C
D
(2).
∵AB//CD
(已知)
∴∠D=∠1
( )
两直线平行,同位角相等
两直线平行,内错角相等
3
.
如图,已知直线a∥b,∠1=50°,求∠2的度数。
分析:由于a∥b,
根据两直线平行,内错角相等,
可得∠1=∠2。
又∠1=50°,因此∠2=50°。
解:∵a∥b(已知)
∴∠1=∠2(两直线平行,内错角相等)
又
∵
∠1=50°(已知)
∴
∠2=50°。
(等量代换)
1.
如图,在四边形ABCD中,已知AB∥CD,∠B=60°,求∠C的度数。能否求得∠A的度数
?
分析:由于AB∥CD
,
根据两直线平行,同旁内角互补
,
可得∠B+∠C=180°
。
又∠B=60°
,因此∠C=120°
。
根据题目的已知条件,无法求出
∠A的度数。
解:∵
AB∥CD
(已知)
∴
∠B+∠C=180°
(两直线平行,同旁内角互补
)
又
∵
∠B=60°
(已知)
∴
∠C=120°
。
(等式的性质)
根据题目的已知条件,无法求出∠A的度数。
初露锋芒
2.
如图,
(1)如果AD∥BC,那么根据两直线平行,同旁内角互补,可得∠____+∠ABC
=180°;
(2)如果AB∥CD,那么根据两直线平行,同旁内角互补,可得∠____+∠ABC
=180°。
(1)
∵
AD∥BC
(已知)
∴∠DAB+∠ABC=180°(两直线平行,
同旁内角互补)
(2)
∵
AB∥CD
(已知)
∴∠DCB+∠ABC=180°(两直线平行,
同旁内角互补)
DAB
DCB
初露锋芒
3.
在图上画着与第三条直线相交的两条平行线,如果∠1=52°
,那么∠2=
,
∠3=
,
∠4=
.
52°
128°
52°
初露锋芒
1.
如图,已知直线a∥b,
∠3=131°,求∠
1、∠2的度数。
解(1)∵∠1=∠3
(对顶角相等)
且∠3=131°(已知)
∴∠1
=131°
(等量代换)
(2)∵a∥b(已知)
∴∠1+∠2=180°(两直线平行,
同旁内角互补)
又
∵
∠1=131°
(已知)
∴
∠2=49°。
(等式性质)
大显身手
大显身手
2.
已知,如图,AC//FD,
试说明:EC//BD
A
B
C
D
E
F
1
2
解:∵
AC//FD
(
)
∴
∠A=∠2
(
)
∵
∠1=∠A,∠B=∠2
(
)
∴
∠1=∠B
(
)
已知
两直线平行,同位角相等
已知
等量代换
∴
EC//BD
(
)
同位角相等,两直线平行
你能解决吗?
已知,如图,AB//CD,则
度。
A
B
C
D
E
A
B
C
D
E
F
解法一:
连结AC
∵
AB//CD
(
)
已知
∴
∠BAC+∠ACD=180
(
)
0
两直线平行,同旁内角互补
三角形内角和
∵
∠E+∠EAC+∠ACE=180
(
)
0
∴
∠BAE+∠E+∠ACE=360
(
)
0
等式性质
解法二:
过点E作EF//AB
360
1、完成教材同步习题;
2、完成练习册本课时对应习题。
课后作业
谢谢欣赏!
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
3.平
行
线
的
性
质
华东师大版
七年级数学上册
教学课件
5.2
平形线
【基本目标】
1.探索平行线的性质,并掌握它们的文字语言、符号语言和图形语言;
2.会用平行线的性质进行简单的计算和推理,结合平行线对图形进行简单的平移.
【学习重点】
掌握平行线的性质.
【学习难点】
平行线的性质的应用.
学习目标
回顾与思考
问题
平行线的判定方法是什么?
1.同位角相等
2.内错角相等
3.同旁内角互补
两直线平行
思考
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
你能解决吗?
已知,如图,AB//CD,则
度。
A
B
C
D
E
知识链接
1.什么叫平行线?
2.指出下图中各对角是哪两条直线被哪一条直线所载
而得到的什么角?
E
A
B
C
D
1
2
3
3.已知,如图,
试说明:
①.
②.
AB//CD
AD//BC
A
B
C
D
解:①
∵
∴
AB//CD
(已知)
(同旁内角互补,两直线平行)
②
∵
∴
(已知)
(等量代换)
∴
AD//BC
(同旁内角互补,两直线平行)
知识积累
1.用前面学过的画平行线的方法
画两条平行线:
a∥b
2.用第三条直线
l
去截这两条平行线,找找其中的同位角、内错角和同旁内角,猜一猜它们的数量关系,并用量角器去测量验证。
3.归纳你得到的结论:
(1)两直线平行,同位角相等
(2)两直线平行,内错角相等,
(3)两直线平行,同旁内角互补,
∵
a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
知识积累
4.概括平行线的性质:
(1).
两直线平行,同位角相等。
(2).
两直线平行,内错角相等。
(3).
两直线平行,同旁内角互补。
5.理解,记忆
(1).区别异同。
(2).与平行线的判定区别。
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行。
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。
平行线的判定
平行线的性质
对
比
1.判断下列说法是否正确。
(1).
对顶角相等。(
)
(2).
相等的角是对顶角。(
)
(3).
两条直线被第三条直线所截,同位角相等。(
)
(4).
如果直线a、b被c所截得的8个角都相等,则a∥b,c⊥a,c⊥b。(
)
√
×
×
√
2.在下列解答中,填上适当的理由。
(1).
∵AD//BC
(已知)
∴∠B=∠1
(
)
1
A
B
C
D
(2).
∵AB//CD
(已知)
∴∠D=∠1
( )
两直线平行,同位角相等
两直线平行,内错角相等
3
.
如图,已知直线a∥b,∠1=50°,求∠2的度数。
分析:由于a∥b,
根据两直线平行,内错角相等,
可得∠1=∠2。
又∠1=50°,因此∠2=50°。
解:∵a∥b(已知)
∴∠1=∠2(两直线平行,内错角相等)
又
∵
∠1=50°(已知)
∴
∠2=50°。
(等量代换)
1.
如图,在四边形ABCD中,已知AB∥CD,∠B=60°,求∠C的度数。能否求得∠A的度数
?
分析:由于AB∥CD
,
根据两直线平行,同旁内角互补
,
可得∠B+∠C=180°
。
又∠B=60°
,因此∠C=120°
。
根据题目的已知条件,无法求出
∠A的度数。
解:∵
AB∥CD
(已知)
∴
∠B+∠C=180°
(两直线平行,同旁内角互补
)
又
∵
∠B=60°
(已知)
∴
∠C=120°
。
(等式的性质)
根据题目的已知条件,无法求出∠A的度数。
初露锋芒
2.
如图,
(1)如果AD∥BC,那么根据两直线平行,同旁内角互补,可得∠____+∠ABC
=180°;
(2)如果AB∥CD,那么根据两直线平行,同旁内角互补,可得∠____+∠ABC
=180°。
(1)
∵
AD∥BC
(已知)
∴∠DAB+∠ABC=180°(两直线平行,
同旁内角互补)
(2)
∵
AB∥CD
(已知)
∴∠DCB+∠ABC=180°(两直线平行,
同旁内角互补)
DAB
DCB
初露锋芒
3.
在图上画着与第三条直线相交的两条平行线,如果∠1=52°
,那么∠2=
,
∠3=
,
∠4=
.
52°
128°
52°
初露锋芒
1.
如图,已知直线a∥b,
∠3=131°,求∠
1、∠2的度数。
解(1)∵∠1=∠3
(对顶角相等)
且∠3=131°(已知)
∴∠1
=131°
(等量代换)
(2)∵a∥b(已知)
∴∠1+∠2=180°(两直线平行,
同旁内角互补)
又
∵
∠1=131°
(已知)
∴
∠2=49°。
(等式性质)
大显身手
大显身手
2.
已知,如图,AC//FD,
试说明:EC//BD
A
B
C
D
E
F
1
2
解:∵
AC//FD
(
)
∴
∠A=∠2
(
)
∵
∠1=∠A,∠B=∠2
(
)
∴
∠1=∠B
(
)
已知
两直线平行,同位角相等
已知
等量代换
∴
EC//BD
(
)
同位角相等,两直线平行
你能解决吗?
已知,如图,AB//CD,则
度。
A
B
C
D
E
A
B
C
D
E
F
解法一:
连结AC
∵
AB//CD
(
)
已知
∴
∠BAC+∠ACD=180
(
)
0
两直线平行,同旁内角互补
三角形内角和
∵
∠E+∠EAC+∠ACE=180
(
)
0
∴
∠BAE+∠E+∠ACE=360
(
)
0
等式性质
解法二:
过点E作EF//AB
360
1、完成教材同步习题;
2、完成练习册本课时对应习题。
课后作业
谢谢欣赏!
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
