第5章 相交线与平行线 本章复习课件(共32张PPT)
文档属性
| 名称 | 第5章 相交线与平行线 本章复习课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 12:31:04 | ||
图片预览




文档简介
(共32张PPT)
本章复习
华东师大版
七年级数学上册
教学课件
第5章
相交线与平行线
【基本目标】
1.经历对本章所学知识回顾与思考的过程,将本章内容条理化、系统化,
梳理本章的知识结构;
2.通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用几何语言说明几何图形;
3.认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质.理解平移的性质,能利用平移设计图案.
【学习重点】
复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用.
【学习难点】
垂直、平行的性质和判定的综合应用.
学习目标
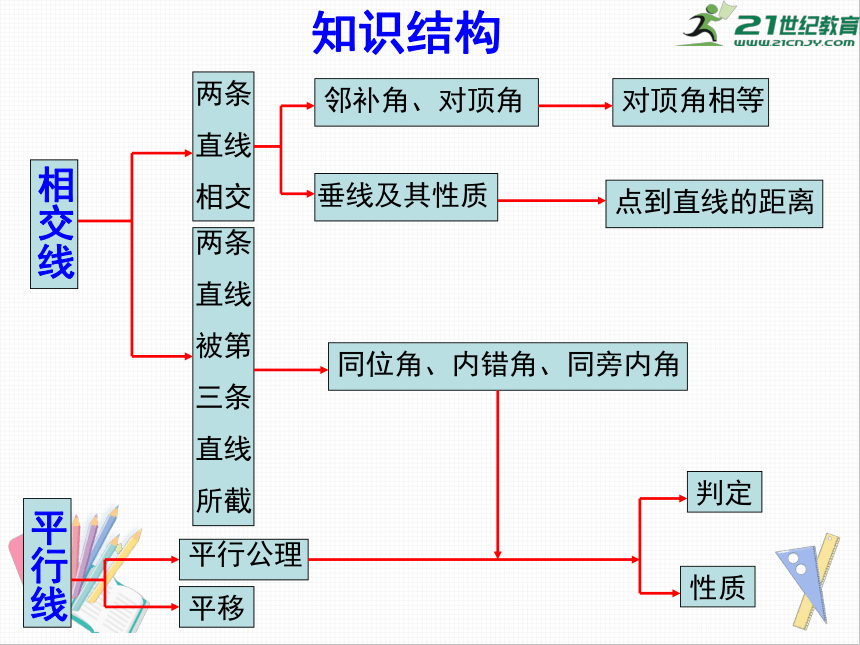
知识结构
相交线
两条
直线
相交
邻补角、对顶角
对顶角相等
垂线及其性质
点到直线的距离
两条
直线
被第
三条
直线
所截
同位角、内错角、同旁内角
平行线
平行公理
平移
判定
性质
1.
互为邻补角:两条直线相交所构成的四了角中,有公共顶点且
有一条公共边的两个角是邻补角。如图(1)
1
2
2.
对顶角:
(1)两条直线相交所构成的四个角中,
(1)
有公共顶点但没有公共边的两个角是对顶角。
如图(2).
(2)
1
2
3
4
(2)一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角。
3.
邻补角的性质:
同角的补角相等。
4.
对顶角性质:对顶角相等。
两个特征:(1)
具有公共顶点;
(2)
角的两边互为反向延长线。
n条直线相交于一点,
就有n(n-1)对对顶角。
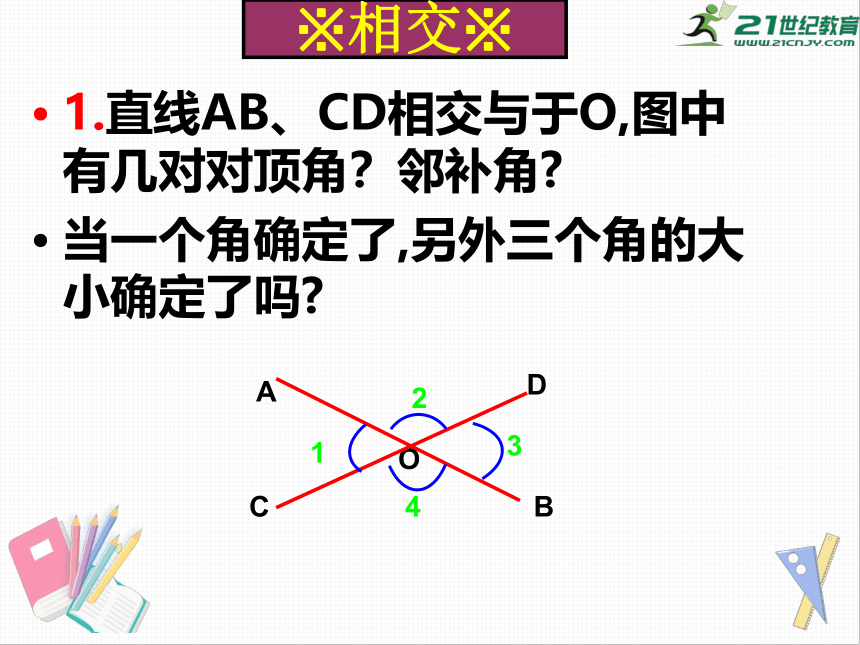
※相交※
1.直线AB、CD相交与于O,图中有几对对顶角?邻补角?
当一个角确定了,另外三个角的大小确定了吗?
O
A
B
C
D
1
2
3
4
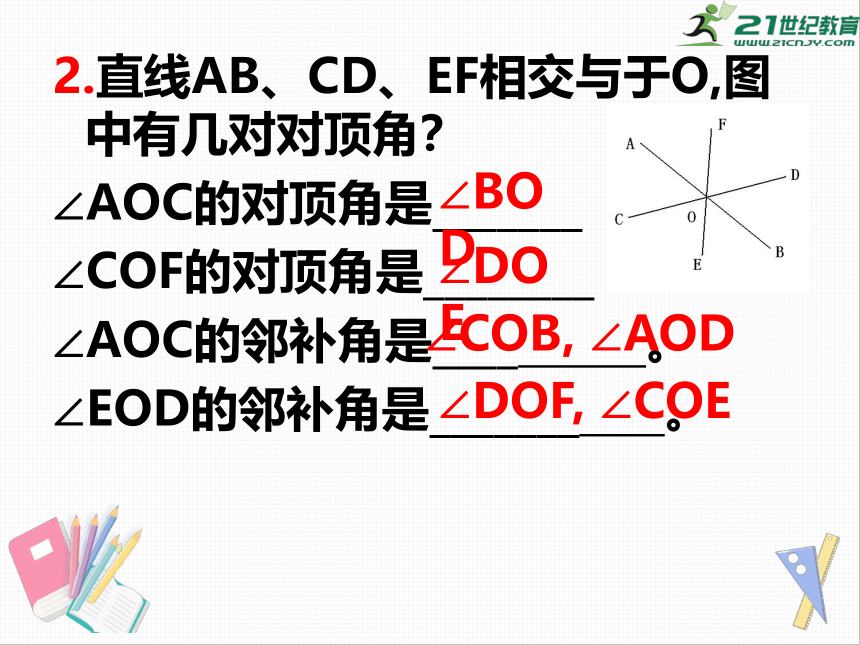
2.直线AB、CD、EF相交与于O,图中有几对对顶角?
∠AOC的对顶角是_______
∠COF的对顶角是________
∠AOC的邻补角是____
。
∠EOD的邻补角是_______
。
∠BOD
∠DOE
∠COB,
∠AOD
∠DOF,
∠COE
A
B
C
D
O
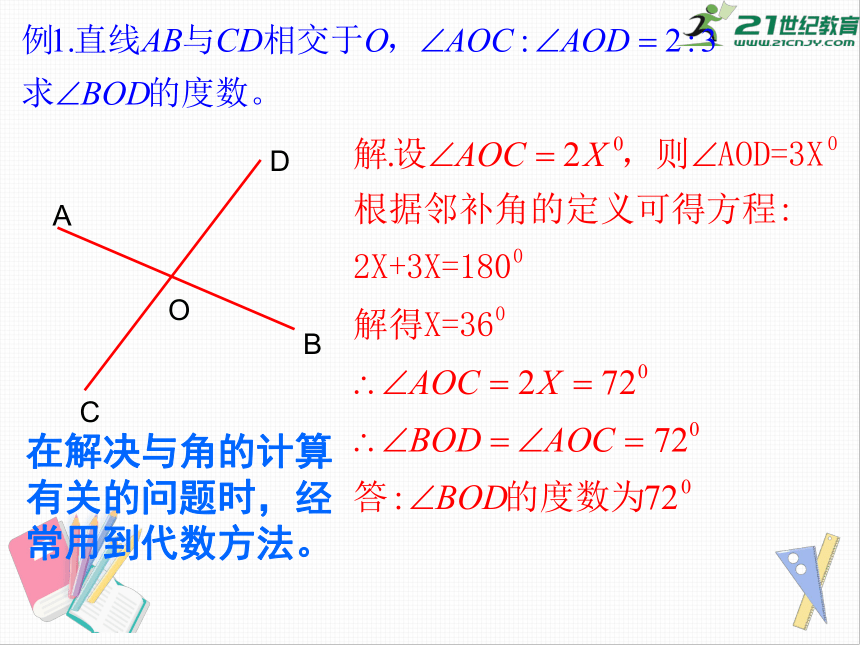
在解决与角的计算有关的问题时,经常用到代数方法。
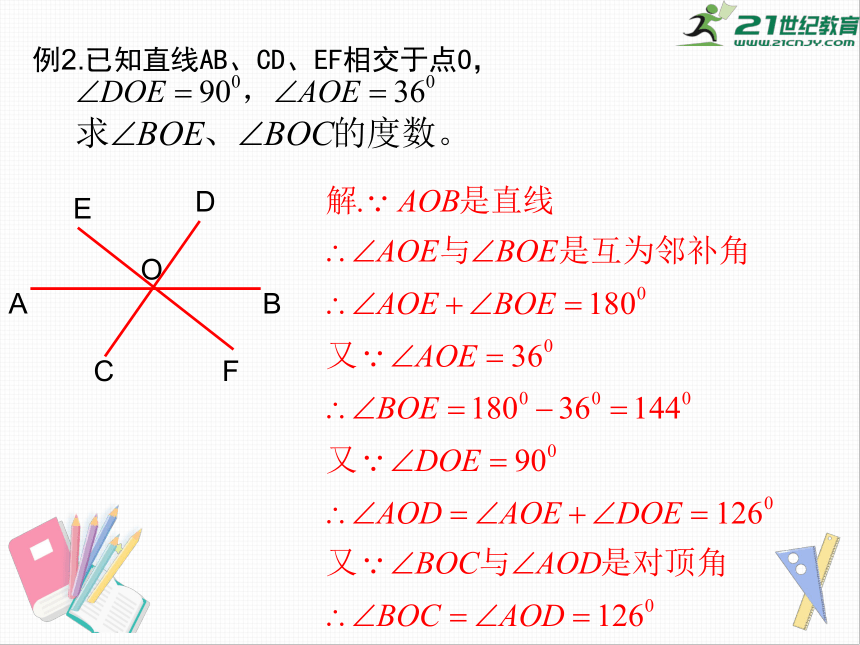
例2.已知直线AB、CD、EF相交于点O,
O
A
B
C
D
E
F
1.垂线的定义:
两条直线相交,所构成的四个角中,有一个角
是
时,就说这两条直线互相垂直。其中一条直线叫做另一
条直线的垂线。它们的交点叫垂足。
2.
垂线的性质:
(1)过一点有且只有一条直线与已知直线垂直。
性质(2):
直线外一点与直线上各点连结的所有线段中,垂线
段最短。简称:垂线段最短。
3.点到直线的距离:
从直线外一点到这条直线的垂线段的长度,
叫做点到直线的距离。
4.如遇到线段与线段,线段与射线,射线与射线,线段或射线与
直线垂直时,特指它们所在的直线互相垂直。
5.垂线是直线,垂线段特指一条线段是图形,点到直线距离是指
垂线段的长度,是指一个数量,是有单位的。
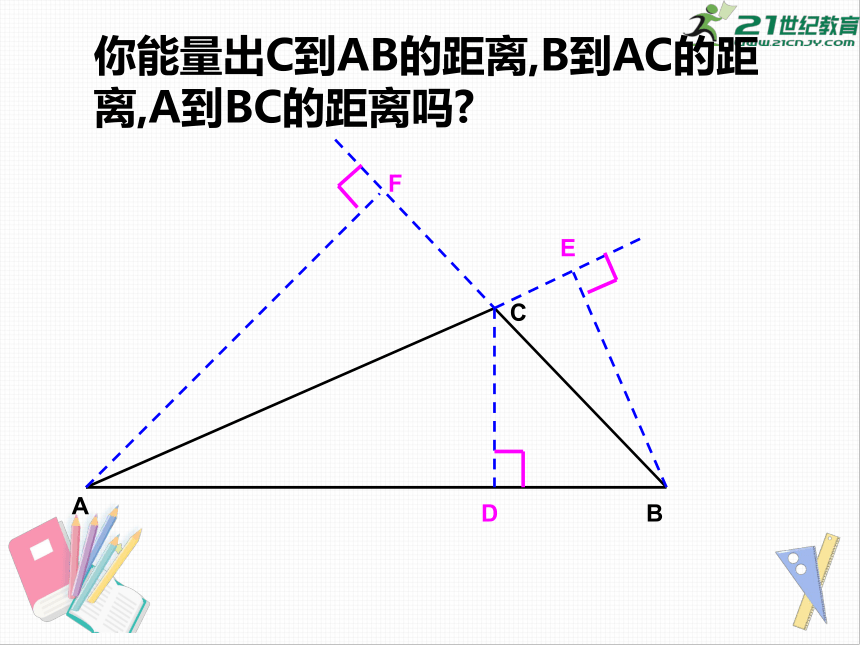
你能量出C到AB的距离,B到AC的距离,A到BC的距离吗?
A
D
C
B
E
F
拓
展
应
用
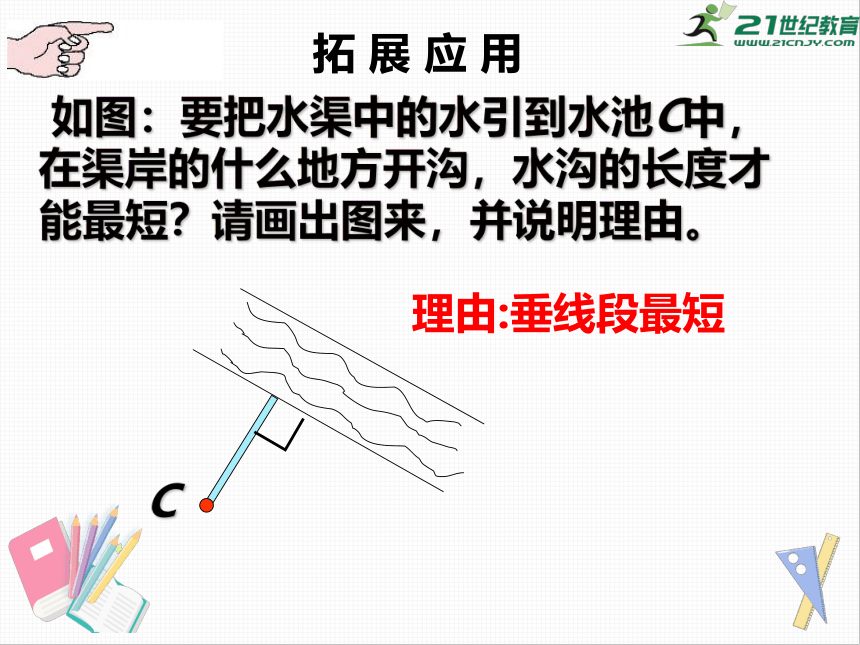
如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。
C
∟
理由:垂线段最短
┓
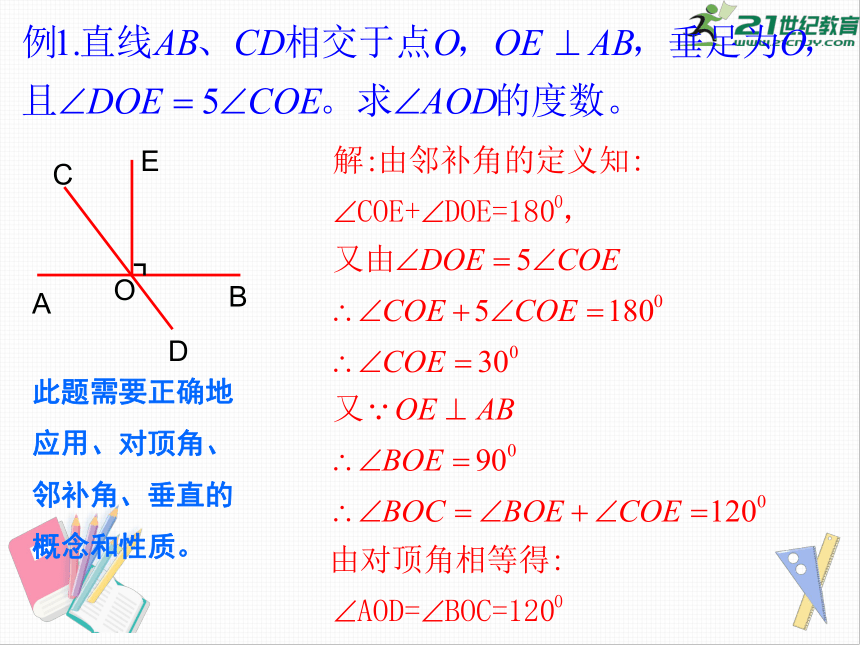
A
B
C
D
O
E
此题需要正确地
应用、对顶角、
邻补角、垂直的
概念和性质。
O
A
D
C
B
由垂直先找到
的
角,再根据角之间
的关系求解。
平行线的概念:
在同一平面内,不相交的两条直线叫做平行线。
2.
两直线的位置关系:
在同一平面内,两直线的位置关系只有两
种:(1)相交;
(2)平行。
3.
平行线的基本性质:
(1)
平行公理(平行线的存在性和唯一性)
经过直线外一点,有且只有一条直线与已知直线平行。
(2)
推论(平行线的传递性)
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行。
4.同位角、内错角、同旁内角的概念
同位角、内错角、同旁内角,指的是一条直线分别与两条直线
相交构成的八个角中,不共顶点的角之间的特殊位置关系。它
们与对顶角、邻补角一样,总是成对存在着的。
同位角的位置特征是:
(1)在截线的同旁,(2)被截两直线的同方向。
内错角的位置特征是:
(1)在截线的两旁,(2)在被截两直线之间。
同旁内角的位置特征是:
(1)在截线的同旁,(2)在被截两直线之间。
判定两直线平行的方法有三种:
(1)定义法;在同一平面内不相交的两条直线是平行线。
(2)传递法;两条直线都和第三条直线平行,这两条直线也平行。
(3)三种角判定(3种方法):
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
在这五种方法中,定义一般不常用。
读下列语句,并画出图形
点p是直线AB外的一点,直线CD经过点P,且与直线AB平行;
直线AB、CD是相交直线,点P是直线AB外的一点,直线EF经过点P与直线AB平行,与直线CD交于E.
.
P
A
B
C
D
C
D
A
B
P
.
E
F
∠1和∠2不是同位角,
练
一
练
如图中的∠1和∠2是同位角吗?
为什么?
1
2
1
2
∵∠1和∠2无一边共线。
∠1和∠2是同位角,
∵∠1和∠2有一边共线、同向
且不共顶点。
如图:直线a、b被直线
l
截的8个角中
同位角:
∠1与∠5
,
∠2与∠6
,
∠3与∠7
,
∠4与∠8.
内错角:
∠3与∠5
,
∠4与∠6.
同旁内角:
∠4与∠5
,
∠3与∠6.
1
4
3
2
8
7
6
5
b
a
l
A
B
D
C
F
E
1
2
3
4
5
6
7
8
9
10
11
12
练一练
(1)∠1和
∠9是由直线
、
被直线
所截成的
角
;
(2)∠6和
∠12是由直线
、
被直线
所截成的
角
;
(3)∠4和
∠6是由直线
、
被直线
所截成的
角
;
(4)由直线AB、CD被直线EF
所截成的同位角有
;
(5)∠7和
∠12是
角
;
在判断两个角时一定要先知道由哪两条直线被哪条直线所截呦!
AB
CD
EF
同位
AB
EF
CD
内错
AB
CD
EF
同旁内
∠1
和∠9、
∠4和
∠12、∠2和∠10、
∠3
和∠11
同旁内
例1.
∠1与哪个角是内错角?
A
C
B
D
E
1
2
答:∠
EAC
答:∠
DAB
答:∠
BAC,∠BAE
,
∠2
∠1与哪个角是同旁内角?
∠2与哪个角是内错角?
1、观察右图并填空:
(1)
∠1
与
是同位角;
(2)
∠5
与
是同旁内角;
(3)
∠1
与
是内错角;
随堂练习
b
a
n
m
2
3
1
4
5
∠4
∠3
∠2
2、
指出图中的同位角、内错角、同旁内角
a
b
l
m
n
1
2
3
4
同位角:∠4与∠1
内错角:∠4与∠2
同旁内角:∠3与∠1
平行线的性质
平行线的判定
两直线平行
条件
结论
同位角相等
内错角相等
同旁内角互补
条件
同位角相等
内错角相等
同旁内角互补
结论
两直线平行
夹在两平行线间的垂线段的长度,叫做两平行线间的距离。
综合应用:
A
B
C
D
E
F
1
2
3
1、填空:
(1)、∵ ∠A=____,
(已知)
AC∥ED
,(_____________________)
(2)、
∵AB
∥______,
(已知)
∠2=
∠4,(______________________)
4
5
(3)、
___
∥___,
(已知)
∠B=
∠3.
(___________
___________)
试一试,你准行!
模仿上题自己编题。(考查平行线的性质或判定)
∠4
同位角相等,两直线平行。
DF
两直线平行,
内错角相等。
AB
DF
两直线平行,
同位角相等.
判定
性质
性质
∴
∴
∴
∵
A
B
C
D
E
F
1
2
3
4
5
6
如图:
填空,并注明理由。
(1)、∵ ∠1=
∠2
(已知)
——∥——
(
)
∵ ∠3=
∠4
(已知)
——∥——
(
)
∵ ∠5=
∠6
(已知)
——∥——
(
)
∵
∠5+
∠AFE=180
(已知)
——∥——
(
)
∵
AB
∥FC,
ED
∥FC
(已知)
——∥——(
)
∴
∴
∴
∴
∴
AB
ED
内错角相等。两直线平行,
AF
BE
同位角相等,两直线平行。
BC
EF
内错角相等,两直线平行。
AF
BE
同旁内角互补,两直线平行。
AB
ED
平行于同直线的两条直线互相平行。
平行线的判定应用练习:
例2.
已知∠DAC=
∠ACB,
∠D+∠DFE=1800,求证:EF//BC
证明:
∵
∠DAC=
∠ACB
(已知)
∴
AD//
BC
(内错角相等,两直线平行)
∵
∠D+∠DFE=1800(已知)
∴
AD//
EF
(同旁内角互补,两直线平行)
∴
EF//
BC
(平行于同一条直线的两条直线互相平行)
A
B
C
D
E
F
例3.
如图
已知:∠1+∠2=180°,
求证:AB∥CD。
证明:由:∠1+∠2=180°(已知),
∠1=∠3(对顶角相等).
∠2=∠4(对顶角相等)
根据:等量代换
得:∠3+∠4=180°.
根据:同旁内角互补,两直线平行
得:AB//CD
.
4
1
2
3
A
B
C
E
F
D
例4.
如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD。
证明:
∵由AC∥DE
(已知)
∴
∠ACD=
∠2
(两直线平行,内错角相等)
∵
∠1=∠2(已知)
∴
∠1=∠ACD(等量代换)
∴AB
∥
CD
(内错角相等,两直线平行)
A
D
B
E
1
2
C
例5.已知
EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。
证明:
∵
EF⊥AB,CD⊥AB
(已知)
∴
AD∥BC
(垂直于同一条直线的两条直线互相平行)
∴
∠EFB=
∠DCB
(两直线平行,同位角相等)
∵
∠EFB=∠GDC
(已知)
∴
∠DCB=∠GDC
(等量代换)
∴
DG∥BC
(内错角相等,两直线平行)
∴
∠AGD=∠ACB
(两直线平行,同位角相等)
例6.
两块平面镜的夹角应为多少度?
如图,两平面镜а、β的夹角为θ,入射光线AO平行于β入
射到а上,经两次反射后的反射光线
平行于а,则角
θ=_____度
а
β
θ
O
B
A
1
2
3
4
5
1、完成教材同步习题;
2、完成练习册本课时对应习题。
课后作业
谢谢欣赏!
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
本章复习
华东师大版
七年级数学上册
教学课件
第5章
相交线与平行线
【基本目标】
1.经历对本章所学知识回顾与思考的过程,将本章内容条理化、系统化,
梳理本章的知识结构;
2.通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用几何语言说明几何图形;
3.认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质.理解平移的性质,能利用平移设计图案.
【学习重点】
复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用.
【学习难点】
垂直、平行的性质和判定的综合应用.
学习目标
知识结构
相交线
两条
直线
相交
邻补角、对顶角
对顶角相等
垂线及其性质
点到直线的距离
两条
直线
被第
三条
直线
所截
同位角、内错角、同旁内角
平行线
平行公理
平移
判定
性质
1.
互为邻补角:两条直线相交所构成的四了角中,有公共顶点且
有一条公共边的两个角是邻补角。如图(1)
1
2
2.
对顶角:
(1)两条直线相交所构成的四个角中,
(1)
有公共顶点但没有公共边的两个角是对顶角。
如图(2).
(2)
1
2
3
4
(2)一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角。
3.
邻补角的性质:
同角的补角相等。
4.
对顶角性质:对顶角相等。
两个特征:(1)
具有公共顶点;
(2)
角的两边互为反向延长线。
n条直线相交于一点,
就有n(n-1)对对顶角。
※相交※
1.直线AB、CD相交与于O,图中有几对对顶角?邻补角?
当一个角确定了,另外三个角的大小确定了吗?
O
A
B
C
D
1
2
3
4
2.直线AB、CD、EF相交与于O,图中有几对对顶角?
∠AOC的对顶角是_______
∠COF的对顶角是________
∠AOC的邻补角是____
。
∠EOD的邻补角是_______
。
∠BOD
∠DOE
∠COB,
∠AOD
∠DOF,
∠COE
A
B
C
D
O
在解决与角的计算有关的问题时,经常用到代数方法。
例2.已知直线AB、CD、EF相交于点O,
O
A
B
C
D
E
F
1.垂线的定义:
两条直线相交,所构成的四个角中,有一个角
是
时,就说这两条直线互相垂直。其中一条直线叫做另一
条直线的垂线。它们的交点叫垂足。
2.
垂线的性质:
(1)过一点有且只有一条直线与已知直线垂直。
性质(2):
直线外一点与直线上各点连结的所有线段中,垂线
段最短。简称:垂线段最短。
3.点到直线的距离:
从直线外一点到这条直线的垂线段的长度,
叫做点到直线的距离。
4.如遇到线段与线段,线段与射线,射线与射线,线段或射线与
直线垂直时,特指它们所在的直线互相垂直。
5.垂线是直线,垂线段特指一条线段是图形,点到直线距离是指
垂线段的长度,是指一个数量,是有单位的。
你能量出C到AB的距离,B到AC的距离,A到BC的距离吗?
A
D
C
B
E
F
拓
展
应
用
如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。
C
∟
理由:垂线段最短
┓
A
B
C
D
O
E
此题需要正确地
应用、对顶角、
邻补角、垂直的
概念和性质。
O
A
D
C
B
由垂直先找到
的
角,再根据角之间
的关系求解。
平行线的概念:
在同一平面内,不相交的两条直线叫做平行线。
2.
两直线的位置关系:
在同一平面内,两直线的位置关系只有两
种:(1)相交;
(2)平行。
3.
平行线的基本性质:
(1)
平行公理(平行线的存在性和唯一性)
经过直线外一点,有且只有一条直线与已知直线平行。
(2)
推论(平行线的传递性)
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行。
4.同位角、内错角、同旁内角的概念
同位角、内错角、同旁内角,指的是一条直线分别与两条直线
相交构成的八个角中,不共顶点的角之间的特殊位置关系。它
们与对顶角、邻补角一样,总是成对存在着的。
同位角的位置特征是:
(1)在截线的同旁,(2)被截两直线的同方向。
内错角的位置特征是:
(1)在截线的两旁,(2)在被截两直线之间。
同旁内角的位置特征是:
(1)在截线的同旁,(2)在被截两直线之间。
判定两直线平行的方法有三种:
(1)定义法;在同一平面内不相交的两条直线是平行线。
(2)传递法;两条直线都和第三条直线平行,这两条直线也平行。
(3)三种角判定(3种方法):
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
在这五种方法中,定义一般不常用。
读下列语句,并画出图形
点p是直线AB外的一点,直线CD经过点P,且与直线AB平行;
直线AB、CD是相交直线,点P是直线AB外的一点,直线EF经过点P与直线AB平行,与直线CD交于E.
.
P
A
B
C
D
C
D
A
B
P
.
E
F
∠1和∠2不是同位角,
练
一
练
如图中的∠1和∠2是同位角吗?
为什么?
1
2
1
2
∵∠1和∠2无一边共线。
∠1和∠2是同位角,
∵∠1和∠2有一边共线、同向
且不共顶点。
如图:直线a、b被直线
l
截的8个角中
同位角:
∠1与∠5
,
∠2与∠6
,
∠3与∠7
,
∠4与∠8.
内错角:
∠3与∠5
,
∠4与∠6.
同旁内角:
∠4与∠5
,
∠3与∠6.
1
4
3
2
8
7
6
5
b
a
l
A
B
D
C
F
E
1
2
3
4
5
6
7
8
9
10
11
12
练一练
(1)∠1和
∠9是由直线
、
被直线
所截成的
角
;
(2)∠6和
∠12是由直线
、
被直线
所截成的
角
;
(3)∠4和
∠6是由直线
、
被直线
所截成的
角
;
(4)由直线AB、CD被直线EF
所截成的同位角有
;
(5)∠7和
∠12是
角
;
在判断两个角时一定要先知道由哪两条直线被哪条直线所截呦!
AB
CD
EF
同位
AB
EF
CD
内错
AB
CD
EF
同旁内
∠1
和∠9、
∠4和
∠12、∠2和∠10、
∠3
和∠11
同旁内
例1.
∠1与哪个角是内错角?
A
C
B
D
E
1
2
答:∠
EAC
答:∠
DAB
答:∠
BAC,∠BAE
,
∠2
∠1与哪个角是同旁内角?
∠2与哪个角是内错角?
1、观察右图并填空:
(1)
∠1
与
是同位角;
(2)
∠5
与
是同旁内角;
(3)
∠1
与
是内错角;
随堂练习
b
a
n
m
2
3
1
4
5
∠4
∠3
∠2
2、
指出图中的同位角、内错角、同旁内角
a
b
l
m
n
1
2
3
4
同位角:∠4与∠1
内错角:∠4与∠2
同旁内角:∠3与∠1
平行线的性质
平行线的判定
两直线平行
条件
结论
同位角相等
内错角相等
同旁内角互补
条件
同位角相等
内错角相等
同旁内角互补
结论
两直线平行
夹在两平行线间的垂线段的长度,叫做两平行线间的距离。
综合应用:
A
B
C
D
E
F
1
2
3
1、填空:
(1)、∵ ∠A=____,
(已知)
AC∥ED
,(_____________________)
(2)、
∵AB
∥______,
(已知)
∠2=
∠4,(______________________)
4
5
(3)、
___
∥___,
(已知)
∠B=
∠3.
(___________
___________)
试一试,你准行!
模仿上题自己编题。(考查平行线的性质或判定)
∠4
同位角相等,两直线平行。
DF
两直线平行,
内错角相等。
AB
DF
两直线平行,
同位角相等.
判定
性质
性质
∴
∴
∴
∵
A
B
C
D
E
F
1
2
3
4
5
6
如图:
填空,并注明理由。
(1)、∵ ∠1=
∠2
(已知)
——∥——
(
)
∵ ∠3=
∠4
(已知)
——∥——
(
)
∵ ∠5=
∠6
(已知)
——∥——
(
)
∵
∠5+
∠AFE=180
(已知)
——∥——
(
)
∵
AB
∥FC,
ED
∥FC
(已知)
——∥——(
)
∴
∴
∴
∴
∴
AB
ED
内错角相等。两直线平行,
AF
BE
同位角相等,两直线平行。
BC
EF
内错角相等,两直线平行。
AF
BE
同旁内角互补,两直线平行。
AB
ED
平行于同直线的两条直线互相平行。
平行线的判定应用练习:
例2.
已知∠DAC=
∠ACB,
∠D+∠DFE=1800,求证:EF//BC
证明:
∵
∠DAC=
∠ACB
(已知)
∴
AD//
BC
(内错角相等,两直线平行)
∵
∠D+∠DFE=1800(已知)
∴
AD//
EF
(同旁内角互补,两直线平行)
∴
EF//
BC
(平行于同一条直线的两条直线互相平行)
A
B
C
D
E
F
例3.
如图
已知:∠1+∠2=180°,
求证:AB∥CD。
证明:由:∠1+∠2=180°(已知),
∠1=∠3(对顶角相等).
∠2=∠4(对顶角相等)
根据:等量代换
得:∠3+∠4=180°.
根据:同旁内角互补,两直线平行
得:AB//CD
.
4
1
2
3
A
B
C
E
F
D
例4.
如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD。
证明:
∵由AC∥DE
(已知)
∴
∠ACD=
∠2
(两直线平行,内错角相等)
∵
∠1=∠2(已知)
∴
∠1=∠ACD(等量代换)
∴AB
∥
CD
(内错角相等,两直线平行)
A
D
B
E
1
2
C
例5.已知
EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。
证明:
∵
EF⊥AB,CD⊥AB
(已知)
∴
AD∥BC
(垂直于同一条直线的两条直线互相平行)
∴
∠EFB=
∠DCB
(两直线平行,同位角相等)
∵
∠EFB=∠GDC
(已知)
∴
∠DCB=∠GDC
(等量代换)
∴
DG∥BC
(内错角相等,两直线平行)
∴
∠AGD=∠ACB
(两直线平行,同位角相等)
例6.
两块平面镜的夹角应为多少度?
如图,两平面镜а、β的夹角为θ,入射光线AO平行于β入
射到а上,经两次反射后的反射光线
平行于а,则角
θ=_____度
а
β
θ
O
B
A
1
2
3
4
5
1、完成教材同步习题;
2、完成练习册本课时对应习题。
课后作业
谢谢欣赏!
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
