平行线的性质

(共10张PPT)
如果两条直线平行
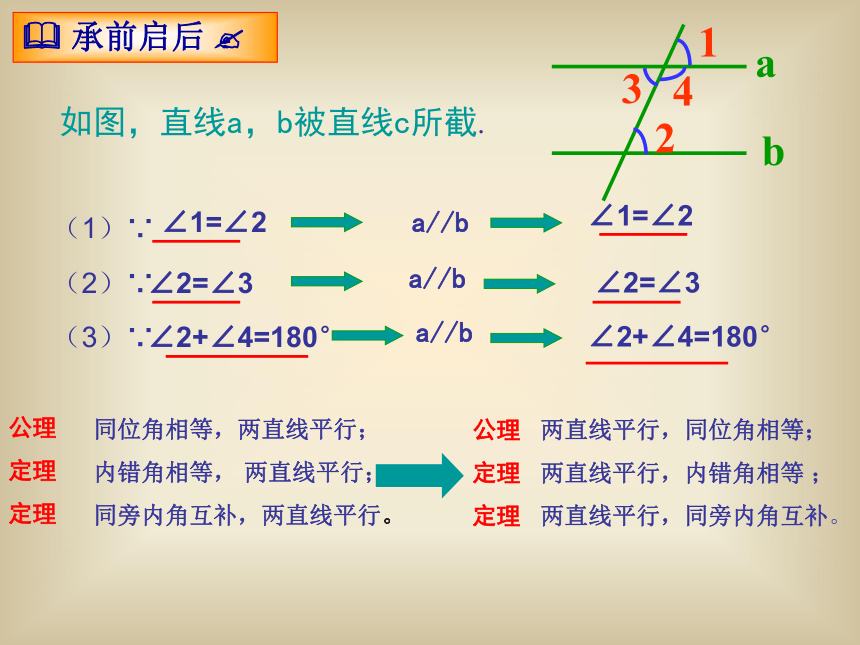
如图，直线a，b被直线c所截.
1
2
3
a
b
4
∠1=∠2
∠2=∠3
∠2+∠4=180°
同位角相等，两直线平行；
内错角相等， 两直线平行；
同旁内角互补，两直线平行。
∠1=∠2
∠2=∠3
∠2+∠4=180°
a//b
a//b
a//b
（1）∵
（2）∵
（3）∵
两直线平行，同位角相等；
两直线平行，内错角相等 ；
两直线平行，同旁内角互补。
公理
定理
定理
公理
定理
定理
承前启后
公理 两条平行线被第三条直线所截，同位角相等.
简单说成: 两直线平行,同位角相等.
利用这个公理,你能证明哪些熟悉的结论
a
b
c
2
1
∴∠1=∠2
∵a // b
温馨提示: 公理是人们公认的真命题,是不需要证明的,除公理外，其他真命题的正确性需要经过推理的方法证实.
探究新知
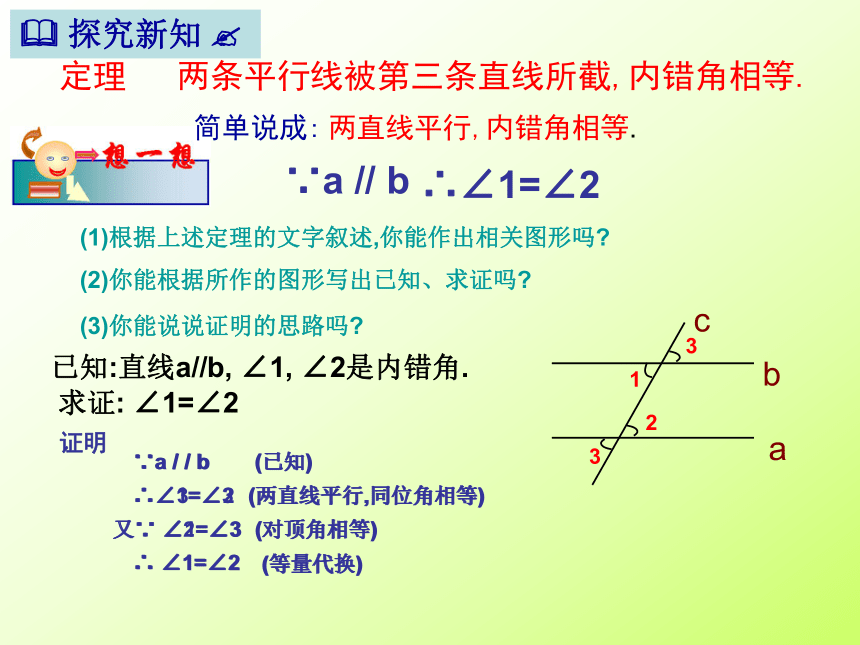
定理 两条平行线被第三条直线所截,内错角相等.
简单说成: 两直线平行,内错角相等.
(1)根据上述定理的文字叙述,你能作出相关图形吗
(2)你能根据所作的图形写出已知、求证吗
(3)你能说说证明的思路吗
已知:直线a//b, ∠1, ∠2是内错角.
求证: ∠1=∠2
∵a / / b
3
a
b
c
2
1
证明
(已知)
∴∠3=∠2
(两直线平行,同位角相等)
又∵ ∠1=∠3
(对顶角相等)
∴ ∠1=∠2
(等量代换)
探究新知
∴∠1=∠2
∵a // b
3
∵a / / b
(已知)
∴∠1=∠3
(两直线平行,同位角相等)
又∵ ∠2=∠3
(对顶角相等)
∴ ∠1=∠2
(等量代换)
文字命题证明的步骤：
1.根据题意，画出图形；
2.根据题设、结论，结合图形，写出
已知、求证；
3.经过分析，找出由已知推出求证的
途径，写出证明过程.
你能说说文字命题证明的一般步骤吗
做一做
证明定理: 两条平行线被第三条直线所截,同旁内角互补.
简单说成: 两直线平行,同旁内角互补
已知: 如图 直线a // b , ∠1和∠2是同旁内角.
求证: ∠1＋∠2=180°
证明
又∵∠1+∠3=180°
∵ a∥b
(已知)
∴∠3=∠2
(两直线平行,同位角相等)
(平角定义)
∴∠1+∠2=180°
(等量代换)
2
3
a
b
1
c
又∵∠1+∠3=180°
∵ a∥b
(已知)
∴∠3=∠2
(两直线平行,内错角相等)
(平角定义)
∴∠1+∠2=180°
(等量代换)
3
3
又∵∠3+∠2=180°
∵ a∥b
(已知)
∴∠1=∠3
(两直线平行,内错角相等)
(平角定义)
∴∠1+∠2=180°
(等量代换)
3
又∵∠3+∠2=180°
∵ a∥b
(已知)
∴∠1=∠3
(两直线平行,同位角相等)
(平角定义)
∴∠1+∠2=180°
(等量代换)
归 纳：
平行线的性质
两直线平行，同位角相等；
两直线平行，内错角相等 ；
两直线平行，同旁内角互补。
公理
定理
定理
点评：公理和已经证明的定理都可以作为以后
推理的依据。
已知: 如图,直线a，b被直线c 所截.a//b.
求证: ∠1＋∠2=180°
2
a
b
1
各抒己见：你想把起过渡桥梁的角添加在什么位置？
说说你的想法？
C
3
3
3
3
课堂小结
这节课你有什么收获吗
1.平行线的性质
两直线平行，同位角相等；
两直线平行，内错角相等 ；
两直线平行，同旁内角互补。
2.证明的一般步骤
（1）根据题意，画出图形；
（2）根据题设、结论，结合图形，写出已知、求证；
（3）经过分析,找出由已知推出求证的途径,写出证
明的过程.