14.1.2 直角三角形的判定 课件(共21张PPT)
文档属性
| 名称 | 14.1.2 直角三角形的判定 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 20:36:50 | ||
图片预览






文档简介
(共21张PPT)
14.1
勾股定理
2.直角三角形的判定
华东师大版
八年级数学上册
上课课件
第14章
勾股定理
情境引入
【基本目标】
1.理解勾股定理的逆定理的证明方法.
2.能用勾股定理的逆定理判别一个三角形是直角三角形.
【教学重点】
用勾股定理的逆定理判别一个三角形是直角三角形.
【教学难点】
勾股定理逆定理的证明.
学习目标
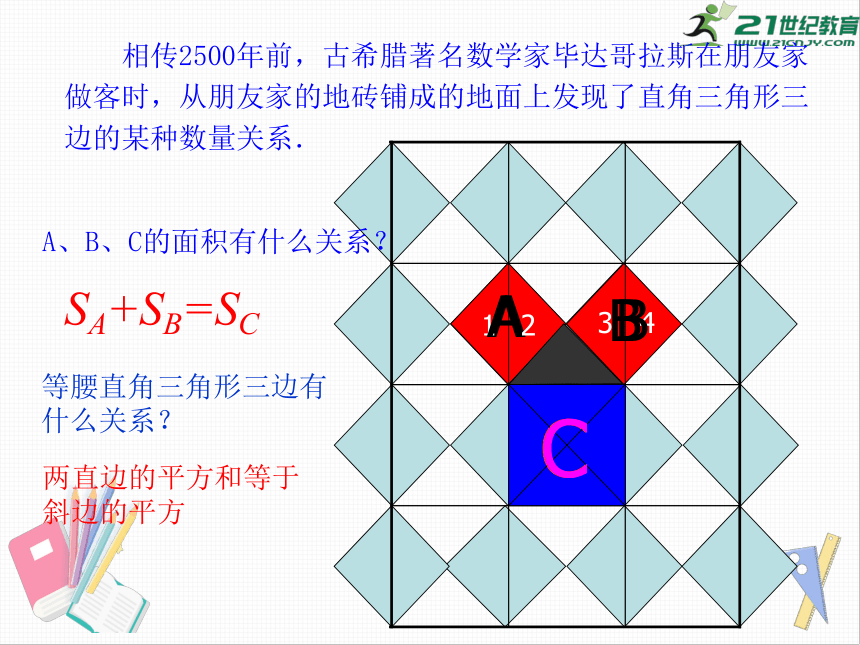
相传2500年前,古希腊著名数学家毕达哥拉斯在朋友家做客时,从朋友家的地砖铺成的地面上发现了直角三角形三边的某种数量关系.
A
B
C
A、B、C的面积有什么关系?
等腰直角三角形三边有
什么关系?
SA+SB=SC
两直边的平方和等于
斜边的平方
1
2
3
4
A
B
C
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
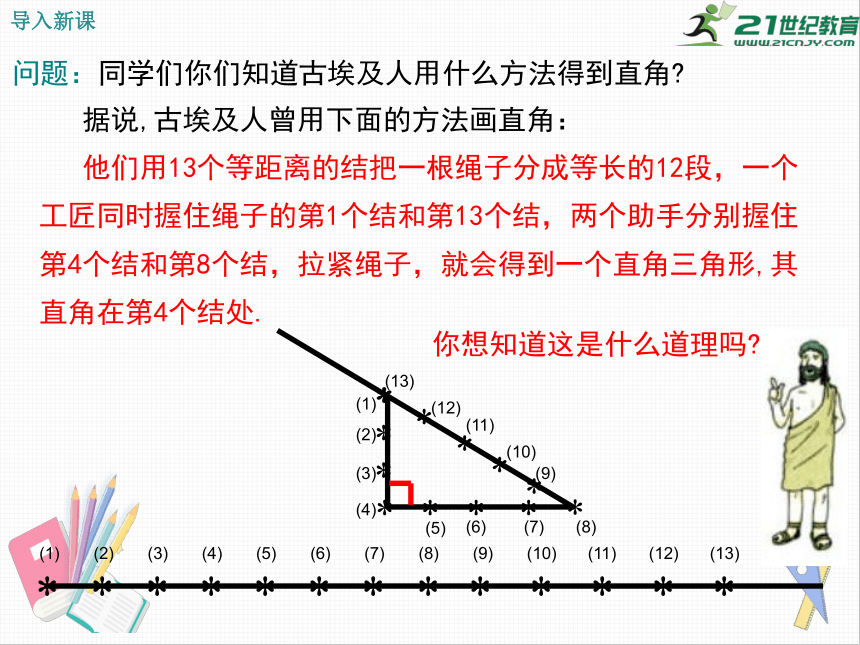
你想知道这是什么道理吗?
据说,古埃及人曾用下面的方法画直角:
他们用13个等距离的结把一根绳子分成等长的12段,一个
工匠同时握住绳子的第1个结和第13个结,两个助手分别握住
第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其
直角在第4个结处.
问题:同学们你们知道古埃及人用什么方法得到直角?
导入新课
直角三角形的判定
一
问题:试画出三边长度分别为如下数据的三角形,看看它们是一些什么样的三角形:
(1)a=3,b=4,c=5;
(2)a=4,b=6,c=8;
(3)a=6,b=8,c=10.
试一试
可以发现,按(1)、(3)所画的三角形都是直角三角形,最长边所对的角是直角;按(2)所画的三角形不是直角三角形.
这三组数都满足
a2+b2=c2吗?
在这三组数据中,(1)、(3)两组数据恰好都满足a2+b2=c2.
勾股定理的逆定理
如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个
三角形是直角三角形,且边c所对的角为直角.
对于任意一个三角形,若三边长满足
a2+b2=c2,则该三角形是直角三角形吗?
B′
C′
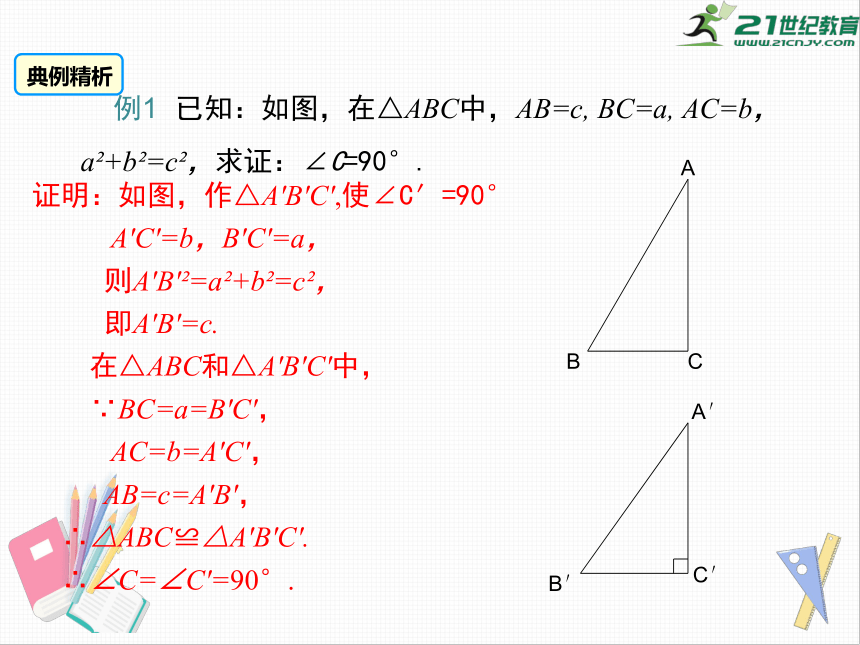
例1
已知:如图,在△ABC中,AB=c,
BC=a,
AC=b,a?+b?=c?,求证:∠C=90°.
A
B
C
A′
证明:如图,作△A'B′C′,使∠C′=90°
A′C′=b,B′C′=a,
则A′B′?=a?+b?=c?,
即A′B′=c.
在△ABC和△A′B′C′中,
∵BC=a=B′C′,
AC=b=A′C′,
AB=c=A′B′,
∴△ABC≌△A′B′C′.
∴∠C=∠C′=90°.
典例精析
分析:根据勾股定理的逆定理,
判断一个三角形是不是直角三角形,
只要看两条较短边长的平方和是否等于最长边长的平方.
例2
判断由线段a,b,c组成的三角形是不是直角三角形?
(1)
a=7,b=25,c=24;
(2)
a=13,b=11,c=9.
解:(1)最长边为25,
∵a2+c2=72+242
=49+576
=625,
b2=252
=625,
∴a2+c2=b2.
∴以7,
25,
24为边长的
三角形是直角三角形.
(2)最长边为13,
∵b2+c2=112+92
=121+81
=202,
a2=132
=169,
∴b2+c2≠a2.
∴以13,
11,
9为边长的
三角形不是直角三角形.
例
3
一个零件的形状如图1所示,按规定这个零件中∠A
和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如
图2所示,你说这个零件符合要求吗?
D
A
B
C
4
3
5
13
12
D
A
B
C
图1
图2
在△BCD中,
所以△BCD
是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
所以△ABD
是直角三角形,∠A是直角.
例4
已知△ABC,AB=n?-1,BC=2n,AC=n?+1(n为大于
1的正整数).试问△ABC是直角三角形吗?若是,哪一条
边所对的角是直角?请说明理由
解:∵AB?+BC?=(n?-1)?+(2n)?
=n4
-2n?+1+4n?
=n4
+2n?+1
=(n?+1)?
=AC?,
∴△ABC直角三角形,边AC所对的角是直角.
先确定AB、BC、AC、
的大小
能够成为直角三角形三边长的三个正整数,称为勾股数.例如3
,4
,5
;6,
8,
10;
n?-1,2n,n?+1(n为大于1的正整数)等都是勾股数.
勾股数
二
例5
下列各组数是勾股数的是(
)
A.6,8,10
B.7,8,9
C.0.3,0.4,0.5
D.52,122,132
A
方法点拨:根据勾股数的定义,勾股数必须为正整数,先排除小数,再计算最长边的平方是否等于其他两边的平方和即可.
当堂练习
1.如果线段a,b,c能组成直角三角形,则它们的比可以是(
)
A.3∶4∶7
B.5∶12∶13
C.1∶2∶4
D.1∶3∶5
将直角三角形的三边长扩大同样的倍数,则得到的
三角形
(
)
A.是直角三角形
B.可能是锐角三角形
C.可能是钝角三角形
D.不可能是直角三角形
B
A
4.如果三条线段a,b,c满足a2=c2-b2,这三条线段组成的
三角形是直角三角形吗?为什么?
解:是直角三角形,因为a2+b2=c2,满足勾股定理的逆定理.
3.以△ABC的三条边为边长向外作正方形,
依次得到的面
积是25,
144
,
169,
则这个三角形是______三角形.
直角
5.如图,在正方形ABCD中,AB=4,AE=2,DF=1,
图中有几个直角三角形,你是如何判断的?
与你的同伴交流.
4
1
2
2
4
3
解:由题意可知△ABE,△DEF,△FCB均为直角三角形.
由勾股定理,知
BE2=22+42=20,EF2=22+12=5,
BF2=32+42=25,
∴BE2+EF2=BF2.
∴
△BEF是直角三角形.
一定是直角三角形
勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形.
课堂小结
勾股数:满足a2+b2=c2的三个正整数
课后作业
1、完成本课时教材对应习题;
2、完成同步练习册本课时对应习题。
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
14.1
勾股定理
2.直角三角形的判定
华东师大版
八年级数学上册
上课课件
第14章
勾股定理
情境引入
【基本目标】
1.理解勾股定理的逆定理的证明方法.
2.能用勾股定理的逆定理判别一个三角形是直角三角形.
【教学重点】
用勾股定理的逆定理判别一个三角形是直角三角形.
【教学难点】
勾股定理逆定理的证明.
学习目标
相传2500年前,古希腊著名数学家毕达哥拉斯在朋友家做客时,从朋友家的地砖铺成的地面上发现了直角三角形三边的某种数量关系.
A
B
C
A、B、C的面积有什么关系?
等腰直角三角形三边有
什么关系?
SA+SB=SC
两直边的平方和等于
斜边的平方
1
2
3
4
A
B
C
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
你想知道这是什么道理吗?
据说,古埃及人曾用下面的方法画直角:
他们用13个等距离的结把一根绳子分成等长的12段,一个
工匠同时握住绳子的第1个结和第13个结,两个助手分别握住
第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其
直角在第4个结处.
问题:同学们你们知道古埃及人用什么方法得到直角?
导入新课
直角三角形的判定
一
问题:试画出三边长度分别为如下数据的三角形,看看它们是一些什么样的三角形:
(1)a=3,b=4,c=5;
(2)a=4,b=6,c=8;
(3)a=6,b=8,c=10.
试一试
可以发现,按(1)、(3)所画的三角形都是直角三角形,最长边所对的角是直角;按(2)所画的三角形不是直角三角形.
这三组数都满足
a2+b2=c2吗?
在这三组数据中,(1)、(3)两组数据恰好都满足a2+b2=c2.
勾股定理的逆定理
如果三角形的三边长a、b、c有关系a2+b2=c2,那么这个
三角形是直角三角形,且边c所对的角为直角.
对于任意一个三角形,若三边长满足
a2+b2=c2,则该三角形是直角三角形吗?
B′
C′
例1
已知:如图,在△ABC中,AB=c,
BC=a,
AC=b,a?+b?=c?,求证:∠C=90°.
A
B
C
A′
证明:如图,作△A'B′C′,使∠C′=90°
A′C′=b,B′C′=a,
则A′B′?=a?+b?=c?,
即A′B′=c.
在△ABC和△A′B′C′中,
∵BC=a=B′C′,
AC=b=A′C′,
AB=c=A′B′,
∴△ABC≌△A′B′C′.
∴∠C=∠C′=90°.
典例精析
分析:根据勾股定理的逆定理,
判断一个三角形是不是直角三角形,
只要看两条较短边长的平方和是否等于最长边长的平方.
例2
判断由线段a,b,c组成的三角形是不是直角三角形?
(1)
a=7,b=25,c=24;
(2)
a=13,b=11,c=9.
解:(1)最长边为25,
∵a2+c2=72+242
=49+576
=625,
b2=252
=625,
∴a2+c2=b2.
∴以7,
25,
24为边长的
三角形是直角三角形.
(2)最长边为13,
∵b2+c2=112+92
=121+81
=202,
a2=132
=169,
∴b2+c2≠a2.
∴以13,
11,
9为边长的
三角形不是直角三角形.
例
3
一个零件的形状如图1所示,按规定这个零件中∠A
和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如
图2所示,你说这个零件符合要求吗?
D
A
B
C
4
3
5
13
12
D
A
B
C
图1
图2
在△BCD中,
所以△BCD
是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
所以△ABD
是直角三角形,∠A是直角.
例4
已知△ABC,AB=n?-1,BC=2n,AC=n?+1(n为大于
1的正整数).试问△ABC是直角三角形吗?若是,哪一条
边所对的角是直角?请说明理由
解:∵AB?+BC?=(n?-1)?+(2n)?
=n4
-2n?+1+4n?
=n4
+2n?+1
=(n?+1)?
=AC?,
∴△ABC直角三角形,边AC所对的角是直角.
先确定AB、BC、AC、
的大小
能够成为直角三角形三边长的三个正整数,称为勾股数.例如3
,4
,5
;6,
8,
10;
n?-1,2n,n?+1(n为大于1的正整数)等都是勾股数.
勾股数
二
例5
下列各组数是勾股数的是(
)
A.6,8,10
B.7,8,9
C.0.3,0.4,0.5
D.52,122,132
A
方法点拨:根据勾股数的定义,勾股数必须为正整数,先排除小数,再计算最长边的平方是否等于其他两边的平方和即可.
当堂练习
1.如果线段a,b,c能组成直角三角形,则它们的比可以是(
)
A.3∶4∶7
B.5∶12∶13
C.1∶2∶4
D.1∶3∶5
将直角三角形的三边长扩大同样的倍数,则得到的
三角形
(
)
A.是直角三角形
B.可能是锐角三角形
C.可能是钝角三角形
D.不可能是直角三角形
B
A
4.如果三条线段a,b,c满足a2=c2-b2,这三条线段组成的
三角形是直角三角形吗?为什么?
解:是直角三角形,因为a2+b2=c2,满足勾股定理的逆定理.
3.以△ABC的三条边为边长向外作正方形,
依次得到的面
积是25,
144
,
169,
则这个三角形是______三角形.
直角
5.如图,在正方形ABCD中,AB=4,AE=2,DF=1,
图中有几个直角三角形,你是如何判断的?
与你的同伴交流.
4
1
2
2
4
3
解:由题意可知△ABE,△DEF,△FCB均为直角三角形.
由勾股定理,知
BE2=22+42=20,EF2=22+12=5,
BF2=32+42=25,
∴BE2+EF2=BF2.
∴
△BEF是直角三角形.
一定是直角三角形
勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形.
课堂小结
勾股数:满足a2+b2=c2的三个正整数
课后作业
1、完成本课时教材对应习题;
2、完成同步练习册本课时对应习题。
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
