14.1.3 反证法 课件(共18张PPT)
文档属性
| 名称 | 14.1.3 反证法 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 20:41:44 | ||
图片预览






文档简介
(共18张PPT)
14.1
勾股定理
3.反证法
华东师大版
八年级数学上册
上课课件
第14章
勾股定理
情境引入
【基本目标】
1.理解反证法.
2.会用反证法证明较简单的题.
【教学重点】
用反证法证明几何命题.
【教学难点】
反证法中渗透“正难则反”的思想.
学习目标
路
边
苦
李
王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.伙伴问他为什么不去摘?
小故事:
新课导入
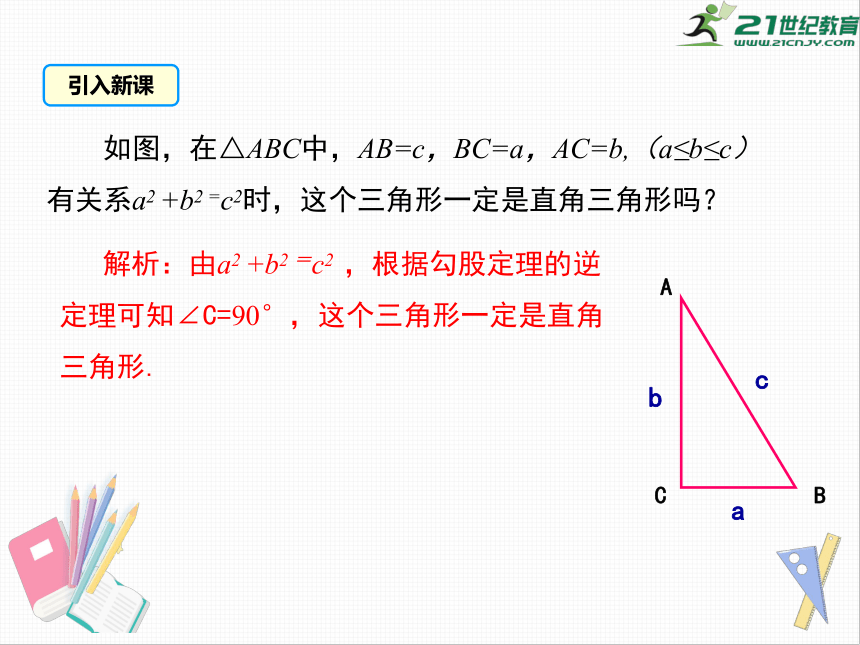
如图,在△ABC中,AB=c,BC=a,AC=b,(a≤b≤c)有关系a2
+b2
=c2时,这个三角形一定是直角三角形吗?
c
a
b
A
C
B
解析:由a2
+b2
=c2
,根据勾股定理的逆定理可知∠C=90°,这个三角形一定是直角三角形.
引入新课
反证法
若将上面的条件改为“在△ABC中,AB=c,BC=a,AC=b(a≤b≤c),a2
+b2
≠
c2”,请问这个三角形是否一定不是直角三角形呢?请说明理由.
c
a
b
A
C
B
探究:
(1)假设它是一个直角三角形;
(2)由勾股定理,一定有a2
+b2
=c2,与已知条件a2
+b2
≠
c2矛盾;
(3)因此假设不成立,即它不是一个直角三角形.
问题探究
这种证明方法与前面的证明方法不同,其步骤为:(1)先假设结论的反面是正确的;
(2)然后通过逻辑推理,得出与基本事实、已证的定理、定义或已知条件相矛盾;
(3)从而说明假设不成立,进而得出原结论正确。
探究发现
像这样的证明方法叫“反证法”.
例1
写出下列各结论的反面:
(1)a∥b;
(2)a≥0;
(3)b是正数;
(4)a⊥b.
a<0
b是0或负数
a不垂直于b
a不平行于b
典例精析
例2
在△ABC中,AB≠AC,求证:∠B
≠
∠
C.
A
B
C
证明:假设 ,
则 (
)
这与 矛盾.
假设不成立.
∴ .
∠B
=
∠C
AB=AC
等角对等边
已知AB≠AC
∠B
≠
∠
C
小结:
反证法的步骤:假设结论的反面成立→逻辑推理得出矛盾→肯定原结论正确
证明:假设a与b不止一个交点,不妨假设有两个交点A和A',
因为两点确定一条直线,即经过点A和A’的直线有且只有一
条,这与已知两条直线矛盾,假设不成立.
所以两条直线相交只有一个交点.
小结:根据假设推出结论除了可以与已知条件矛盾以外,还可以与我们学过的基本事实、定理矛盾.
例3
求证:两条直线相交只有一个交点.
已知:如图,两条相交直线a,b.
求证:a与b只有一个交点.
a
b
A
●
A'
●
分析:想从已知条件“两条相交直线a,b”出发,经过推理,得出结论“a,b只有一个交点”是很困难的,因此可以考虑用反证法.
例4
求证:在一个三角形中,至少有一个内角小于或等于60°.
已知:△ABC.
求证:△ABC中至少有一个内角小于或等于60°.
证明:假设 ,
即 ,
∴ ,
这与 矛盾.假设不成立.
∴ .
△ABC中没有一个内角小于或等于60°
∠A>60°,∠B>60°,∠C>60°
三角形的内角和为180°
△ABC中至少有一个内角小于或等于60°
点拨:至少的反面是没有!
∠A+∠B+∠C>60°+60°+60°=180°
1.试说出下列命题的反面:
(1)a是实数;
(2)a大于2;
(3)a小于2;
(4)至少有2个;
(5)最多有一个;
(6)两条直线平行;
2.用反证法证明“若a2≠
b2,则a
≠
b”的第一步是
.
3.用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步
.
a不是实数
a小于或等于2
a大于或等于2
没有两个
一个也没有
两直线相交
假设a=b
假设这个三角形是等腰三角形
当堂练习
4.命题“三角形中最多只有一个内角是直角”的结论的否定是(
)
A.有两个内角是直角
B.有三个内角是直角
C.至少有两个内角是直角
D.没有一个内角是直角
5.否定“自然数a,b,c中恰有一个偶数”时,正确的反设为(
)
A.a,b,c都是奇数
B.
a,b,c都是偶数
C.
a,b,c中至少有两个偶数
D.
a,b,c中都是奇数或至少有两个偶数
C
D
6.已知:a是整数,2能整除a2.
求证:2能整除a.
证明:假设命题的结论不成立,即“2不能整除a”,因为a是整数,故a是奇数.
不妨设a=2n+1(n是整数),
∴a2=(2n+1)2=4n2+4n+1=2(2n2+2n)+1,
∴a2是奇数,则2不能整除a2
,这与已知矛盾.
∴假设不成立,故2能整除a.
原词语
否定词
原词语
否定词
等于
任意的
是
至少有一个
都是
至多有一个
大于
至少有n个
小于
至多有n个
对所有x成立
对任何x
不成立
7.准确地作出反设(即否定结论)是非常重要的,下面是一些常见的关键词的否定形式.
?
不是
不都是
不大于
不小于
一个也没有
至少有两个
至多有(n-1)个
至少有(n+1)个
存在某个x不成立
存在某个x成立
不等于
某个
反证法
概念
课堂小结
反证法证明的思路:假设命题不成立→正确的推理,得出矛盾→肯定待定命题的结论.
证明步骤
课后作业
1、完成本课时教材对应习题;
2、完成同步练习册本课时对应习题。
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
14.1
勾股定理
3.反证法
华东师大版
八年级数学上册
上课课件
第14章
勾股定理
情境引入
【基本目标】
1.理解反证法.
2.会用反证法证明较简单的题.
【教学重点】
用反证法证明几何命题.
【教学难点】
反证法中渗透“正难则反”的思想.
学习目标
路
边
苦
李
王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.伙伴问他为什么不去摘?
小故事:
新课导入
如图,在△ABC中,AB=c,BC=a,AC=b,(a≤b≤c)有关系a2
+b2
=c2时,这个三角形一定是直角三角形吗?
c
a
b
A
C
B
解析:由a2
+b2
=c2
,根据勾股定理的逆定理可知∠C=90°,这个三角形一定是直角三角形.
引入新课
反证法
若将上面的条件改为“在△ABC中,AB=c,BC=a,AC=b(a≤b≤c),a2
+b2
≠
c2”,请问这个三角形是否一定不是直角三角形呢?请说明理由.
c
a
b
A
C
B
探究:
(1)假设它是一个直角三角形;
(2)由勾股定理,一定有a2
+b2
=c2,与已知条件a2
+b2
≠
c2矛盾;
(3)因此假设不成立,即它不是一个直角三角形.
问题探究
这种证明方法与前面的证明方法不同,其步骤为:(1)先假设结论的反面是正确的;
(2)然后通过逻辑推理,得出与基本事实、已证的定理、定义或已知条件相矛盾;
(3)从而说明假设不成立,进而得出原结论正确。
探究发现
像这样的证明方法叫“反证法”.
例1
写出下列各结论的反面:
(1)a∥b;
(2)a≥0;
(3)b是正数;
(4)a⊥b.
a<0
b是0或负数
a不垂直于b
a不平行于b
典例精析
例2
在△ABC中,AB≠AC,求证:∠B
≠
∠
C.
A
B
C
证明:假设 ,
则 (
)
这与 矛盾.
假设不成立.
∴ .
∠B
=
∠C
AB=AC
等角对等边
已知AB≠AC
∠B
≠
∠
C
小结:
反证法的步骤:假设结论的反面成立→逻辑推理得出矛盾→肯定原结论正确
证明:假设a与b不止一个交点,不妨假设有两个交点A和A',
因为两点确定一条直线,即经过点A和A’的直线有且只有一
条,这与已知两条直线矛盾,假设不成立.
所以两条直线相交只有一个交点.
小结:根据假设推出结论除了可以与已知条件矛盾以外,还可以与我们学过的基本事实、定理矛盾.
例3
求证:两条直线相交只有一个交点.
已知:如图,两条相交直线a,b.
求证:a与b只有一个交点.
a
b
A
●
A'
●
分析:想从已知条件“两条相交直线a,b”出发,经过推理,得出结论“a,b只有一个交点”是很困难的,因此可以考虑用反证法.
例4
求证:在一个三角形中,至少有一个内角小于或等于60°.
已知:△ABC.
求证:△ABC中至少有一个内角小于或等于60°.
证明:假设 ,
即 ,
∴ ,
这与 矛盾.假设不成立.
∴ .
△ABC中没有一个内角小于或等于60°
∠A>60°,∠B>60°,∠C>60°
三角形的内角和为180°
△ABC中至少有一个内角小于或等于60°
点拨:至少的反面是没有!
∠A+∠B+∠C>60°+60°+60°=180°
1.试说出下列命题的反面:
(1)a是实数;
(2)a大于2;
(3)a小于2;
(4)至少有2个;
(5)最多有一个;
(6)两条直线平行;
2.用反证法证明“若a2≠
b2,则a
≠
b”的第一步是
.
3.用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步
.
a不是实数
a小于或等于2
a大于或等于2
没有两个
一个也没有
两直线相交
假设a=b
假设这个三角形是等腰三角形
当堂练习
4.命题“三角形中最多只有一个内角是直角”的结论的否定是(
)
A.有两个内角是直角
B.有三个内角是直角
C.至少有两个内角是直角
D.没有一个内角是直角
5.否定“自然数a,b,c中恰有一个偶数”时,正确的反设为(
)
A.a,b,c都是奇数
B.
a,b,c都是偶数
C.
a,b,c中至少有两个偶数
D.
a,b,c中都是奇数或至少有两个偶数
C
D
6.已知:a是整数,2能整除a2.
求证:2能整除a.
证明:假设命题的结论不成立,即“2不能整除a”,因为a是整数,故a是奇数.
不妨设a=2n+1(n是整数),
∴a2=(2n+1)2=4n2+4n+1=2(2n2+2n)+1,
∴a2是奇数,则2不能整除a2
,这与已知矛盾.
∴假设不成立,故2能整除a.
原词语
否定词
原词语
否定词
等于
任意的
是
至少有一个
都是
至多有一个
大于
至少有n个
小于
至多有n个
对所有x成立
对任何x
不成立
7.准确地作出反设(即否定结论)是非常重要的,下面是一些常见的关键词的否定形式.
?
不是
不都是
不大于
不小于
一个也没有
至少有两个
至多有(n-1)个
至少有(n+1)个
存在某个x不成立
存在某个x成立
不等于
某个
反证法
概念
课堂小结
反证法证明的思路:假设命题不成立→正确的推理,得出矛盾→肯定待定命题的结论.
证明步骤
课后作业
1、完成本课时教材对应习题;
2、完成同步练习册本课时对应习题。
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
