江西省萍乡市2020-2021年度高三第一学期数学期中复习试卷(理科)(PDF版无答案)
文档属性
| 名称 | 江西省萍乡市2020-2021年度高三第一学期数学期中复习试卷(理科)(PDF版无答案) |
|
|
| 格式 | |||
| 文件大小 | 203.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-23 00:00:00 | ||
图片预览

文档简介
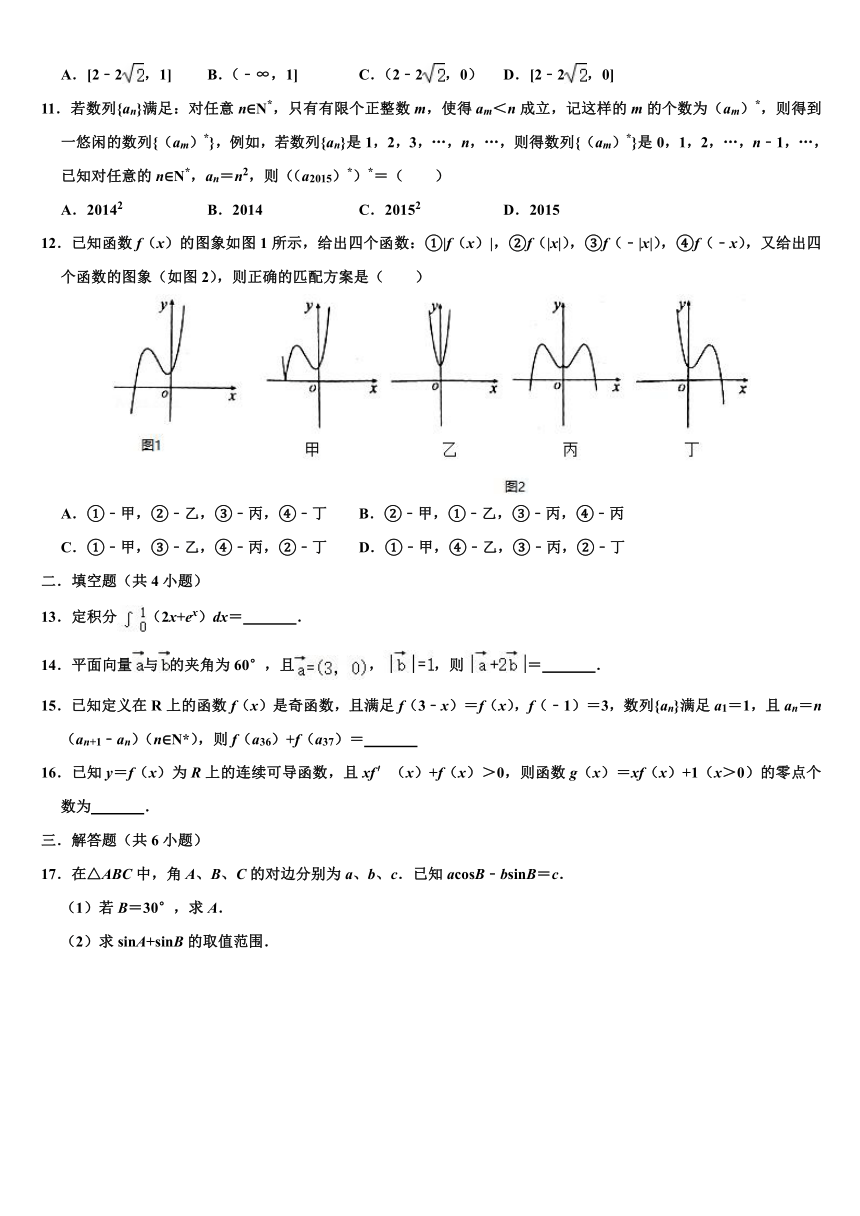
江西省萍乡市 2020-2021 年度高三上学期期中复习试卷(理科)
一.选择题(共12小题)
1.若集合A={x|y=2x},集合 ,则A∩B=( )
A.(0,+∞) B.(1,+∞) C.[0,+∞) D.(﹣∞,+∞)
2.已知等差数列{an}的前n项和为Sn,a1=﹣3,2a4+3a7=9,则S7的值等于( )
A.21 B.1 C.﹣42 D.0
3.已知函数f(x)是定义在R上的偶函数,且f(x)在[0,+∞)上单调递增,若f(2)=3,则满足f(x+1)<3
的x的取值范围是( )
A.(﹣∞,﹣2)∪(0,2) B.(﹣2,2) C.(﹣∞,﹣3)∪(0,1) D.(﹣3,1)
4.已知集合A={x|x2﹣x﹣2<0},B={x||x|>1},则A∩B=( )
A.(﹣2,﹣1) B.(﹣1,1) C.(0,1) D.(1,2)
5.已知 ,且 ,则tan =( )
θ
A.2 B. C.3 D.
6.函数f(x)= 的部分图象大致是( )
A. B. C. D.
7.如图,O为△ABC的外心,AB=4,AC=2,∠BAC为钝角,M是边BC的中点,则 的值( )
A. B.12 C.6 D.5
8.已知实数x,y满足约束条件 ,目标函数z=ax+by(a>0且b>0)的最大值为2,
则 + 的最小值为( )
A. + B. + C.3+2 D.5+6
9.在△ABC中,角A,B,C的对边分别是a,b,c,且A,B,C成等差,b=1,则a+c的取值范围是( )
A.(1,2] B.(0,2] C.(1, ] D.(0, ]
10.已知函数f(x)= ,若f(x)≥ax恒成立,则实数a的取值范围是( )
A.[2﹣2 ,1] B.(﹣∞,1] C.(2﹣2 ,0) D.[2﹣2 ,0]
11.若数列{an}满足:对任意n N*,只有有限个正整数m,使得am<n成立,记这样的m的个数为(am)*,则得到
一悠闲的数列{(am)*},例如∈
,若数列{an}是1,2,3,…,n,…,则得数列{(am)*}是0,1,2,…,n﹣1,…,
已知对任意的n N*,an=n2,则((a2015)*)*=( )
A.20142 ∈
B.2014 C.20152 D.2015
12.已知函数f(x)的图象如图1所示,给出四个函数: |f(x)|, f(|x|), f(﹣|x|), f(﹣x),又给出四
个函数的图象(如图2),则正确的匹配方案是( )① ② ③ ④
A. ﹣甲, ﹣乙, ﹣丙, ﹣丁 B. ﹣甲, ﹣乙, ﹣丙, ﹣丙
C.①
﹣甲,②
﹣乙,③
﹣丙,④
﹣丁 D.②
﹣甲,①
﹣乙,③
﹣丙,④
﹣丁
二.填空①
题(共③
4小题) ④ ② ① ④ ③ ②
13.定积分 (2x+ex)dx= .
14.平面向量 与 的夹角为60°,且 , ,则 = .
15.已知定义在R上的函数f(x)是奇函数,且满足f(3﹣x)=f(x),f(﹣1)=3,数列{an}满足a1=1,且an=n
(an+1﹣an)(n N*),则f(a36)+f(a37)=
16.已知y=f(x)∈
为R上的连续可导函数,且xf′(x)+f(x)>0,则函数g(x)=xf(x)+1(x>0)的零点个
数为 .
三.解答题(共6小题)
17.在△ABC中,角A、B、C的对边分别为a、b、c.已知acosB﹣bsinB=c.
(1)若B=30°,求A.
(2)求sinA+sinB的取值范围.
18.直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB=2,E为BB1延长线上的一点,
D1E⊥面D1AC.
(1)若H是BB1的中点,证明:DH∥D1E;
(2)求三棱锥A﹣CDE的体积;
(3)求二面角E﹣AC﹣D1的大小.
19.每年的12月4日为我国“法制宣传日”.天津市某高中团委在2019年12月4日开展了以“学法、遵法、守法”
为主题的学习活动.已知该学校高一、高二、高三的学生人数分别是480人、360人、360人.为检查该学校组织
学生学习的效果,现采用分层抽样的方法从该校全体学生中选取10名学生进行问卷测试.具体要求:每位被选中
的学生要从10个有关法律、法规的问题中随机抽出4个问题进行作答,所抽取的4个问题全部答对的学生将在全
校给予表彰.
(1)求各个年级应选取的学生人数;
(2)若从被选取的10名学生中任选3人,求这3名学生分别来自三个年级的概率;
(3)若被选取的10人中的某学生能答对10道题中的7道题,另外3道题回答不对,记X表示该名学生答对问题
的个数,求随机变量X的分布列及数学期望.
20.已知{an}为等差数列,前n项和为Sn(n N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4﹣
2a1,S11=11b4. ∈
(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{an?bn}的前n项和为Tn(n N*).
∈
21.已知函数f (x)=ex﹣ax2,g(x)=xlnx﹣x2+(e﹣1)x+1,且曲线y=f(x)在x=1处的切线方程为y=bx+1.
(1)求a,b的值;
(2)求函数f(x)在[0,1]上的最小值:
(3)证明:当x>0时,g(x)≤f( x).
22.已知函数f(x)=e|x|+|x﹣a|是偶函数.
(Ⅰ)求曲线y=f(x)在x=1处的切线方程;
(Ⅱ)求不等式f(x)≥x的解集.
一.选择题(共12小题)
1.若集合A={x|y=2x},集合 ,则A∩B=( )
A.(0,+∞) B.(1,+∞) C.[0,+∞) D.(﹣∞,+∞)
2.已知等差数列{an}的前n项和为Sn,a1=﹣3,2a4+3a7=9,则S7的值等于( )
A.21 B.1 C.﹣42 D.0
3.已知函数f(x)是定义在R上的偶函数,且f(x)在[0,+∞)上单调递增,若f(2)=3,则满足f(x+1)<3
的x的取值范围是( )
A.(﹣∞,﹣2)∪(0,2) B.(﹣2,2) C.(﹣∞,﹣3)∪(0,1) D.(﹣3,1)
4.已知集合A={x|x2﹣x﹣2<0},B={x||x|>1},则A∩B=( )
A.(﹣2,﹣1) B.(﹣1,1) C.(0,1) D.(1,2)
5.已知 ,且 ,则tan =( )
θ
A.2 B. C.3 D.
6.函数f(x)= 的部分图象大致是( )
A. B. C. D.
7.如图,O为△ABC的外心,AB=4,AC=2,∠BAC为钝角,M是边BC的中点,则 的值( )
A. B.12 C.6 D.5
8.已知实数x,y满足约束条件 ,目标函数z=ax+by(a>0且b>0)的最大值为2,
则 + 的最小值为( )
A. + B. + C.3+2 D.5+6
9.在△ABC中,角A,B,C的对边分别是a,b,c,且A,B,C成等差,b=1,则a+c的取值范围是( )
A.(1,2] B.(0,2] C.(1, ] D.(0, ]
10.已知函数f(x)= ,若f(x)≥ax恒成立,则实数a的取值范围是( )
A.[2﹣2 ,1] B.(﹣∞,1] C.(2﹣2 ,0) D.[2﹣2 ,0]
11.若数列{an}满足:对任意n N*,只有有限个正整数m,使得am<n成立,记这样的m的个数为(am)*,则得到
一悠闲的数列{(am)*},例如∈
,若数列{an}是1,2,3,…,n,…,则得数列{(am)*}是0,1,2,…,n﹣1,…,
已知对任意的n N*,an=n2,则((a2015)*)*=( )
A.20142 ∈
B.2014 C.20152 D.2015
12.已知函数f(x)的图象如图1所示,给出四个函数: |f(x)|, f(|x|), f(﹣|x|), f(﹣x),又给出四
个函数的图象(如图2),则正确的匹配方案是( )① ② ③ ④
A. ﹣甲, ﹣乙, ﹣丙, ﹣丁 B. ﹣甲, ﹣乙, ﹣丙, ﹣丙
C.①
﹣甲,②
﹣乙,③
﹣丙,④
﹣丁 D.②
﹣甲,①
﹣乙,③
﹣丙,④
﹣丁
二.填空①
题(共③
4小题) ④ ② ① ④ ③ ②
13.定积分 (2x+ex)dx= .
14.平面向量 与 的夹角为60°,且 , ,则 = .
15.已知定义在R上的函数f(x)是奇函数,且满足f(3﹣x)=f(x),f(﹣1)=3,数列{an}满足a1=1,且an=n
(an+1﹣an)(n N*),则f(a36)+f(a37)=
16.已知y=f(x)∈
为R上的连续可导函数,且xf′(x)+f(x)>0,则函数g(x)=xf(x)+1(x>0)的零点个
数为 .
三.解答题(共6小题)
17.在△ABC中,角A、B、C的对边分别为a、b、c.已知acosB﹣bsinB=c.
(1)若B=30°,求A.
(2)求sinA+sinB的取值范围.
18.直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB=2,E为BB1延长线上的一点,
D1E⊥面D1AC.
(1)若H是BB1的中点,证明:DH∥D1E;
(2)求三棱锥A﹣CDE的体积;
(3)求二面角E﹣AC﹣D1的大小.
19.每年的12月4日为我国“法制宣传日”.天津市某高中团委在2019年12月4日开展了以“学法、遵法、守法”
为主题的学习活动.已知该学校高一、高二、高三的学生人数分别是480人、360人、360人.为检查该学校组织
学生学习的效果,现采用分层抽样的方法从该校全体学生中选取10名学生进行问卷测试.具体要求:每位被选中
的学生要从10个有关法律、法规的问题中随机抽出4个问题进行作答,所抽取的4个问题全部答对的学生将在全
校给予表彰.
(1)求各个年级应选取的学生人数;
(2)若从被选取的10名学生中任选3人,求这3名学生分别来自三个年级的概率;
(3)若被选取的10人中的某学生能答对10道题中的7道题,另外3道题回答不对,记X表示该名学生答对问题
的个数,求随机变量X的分布列及数学期望.
20.已知{an}为等差数列,前n项和为Sn(n N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4﹣
2a1,S11=11b4. ∈
(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{an?bn}的前n项和为Tn(n N*).
∈
21.已知函数f (x)=ex﹣ax2,g(x)=xlnx﹣x2+(e﹣1)x+1,且曲线y=f(x)在x=1处的切线方程为y=bx+1.
(1)求a,b的值;
(2)求函数f(x)在[0,1]上的最小值:
(3)证明:当x>0时,g(x)≤f( x).
22.已知函数f(x)=e|x|+|x﹣a|是偶函数.
(Ⅰ)求曲线y=f(x)在x=1处的切线方程;
(Ⅱ)求不等式f(x)≥x的解集.
同课章节目录
