人教版七上数学单元卷(二):第二章 整式的加减 习题课件(26张PPT)
文档属性
| 名称 | 人教版七上数学单元卷(二):第二章 整式的加减 习题课件(26张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 762.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-21 00:00:00 | ||
图片预览







文档简介
单元卷(二) 整式的加减
测试范围:第二章
选择题
填空题
解答题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
一、选择题(每小题3分,共30分)
1.在式子ab,-6, , , ,- ,m2+2m-1,-p3q中,整式有( )
A.5个 B.6个
C.7个 D.8个
B
2.下列选项中,两个单项式属于同类项的是( )
A.a3与b3 B.3x2y与-4x2yz
C.x2y与-xy2 D.-2a2b与ba2
3.“a与b的平方的和”用式子表示正确的是( )
A.a2+b B.(a+b)2
C.a+b2 D.a2+b2
D
C
4.下列计算结果正确的是( )
A.2x+3y=5xy B.5a2+3a2=8a4
C.3xy-5yx=-2xy D.4a2b-5ab2=-a2b
5.下列去括号正确的是( )
A.x-(-2x2+x3)=x+2x2-x3 B.-(a+b)=-a+b
C.2(a+b)=2a-2b D.-x-(y-z)=-x-y-z
C
A
6.下列说法正确的是( )
A.-3πa2b的系数是-3 B. xy2的次数是2
C.-2x3+3x2-x的次数是6 D.a2-2a-3的常数项是-3
7.某超市一商品的进价为m元,将其价格提高50%作为零售价,半年后又以六折的价格促销,则此时这一商品的价格为( )
A.m元 B.0.9m元
C.0.92m元 D.1.04m元
D
B
8.若a-b=-1,则式子(a-b)2-3a+3b的值是( )
A.4 B.3
C.2 D.-2
9.长方形的一边长是4x+y,另一边比它短x-y,则长方形的周长是( )
A.7x+y B.7x+3y
C.14x+2y D.14x+6y
A
D
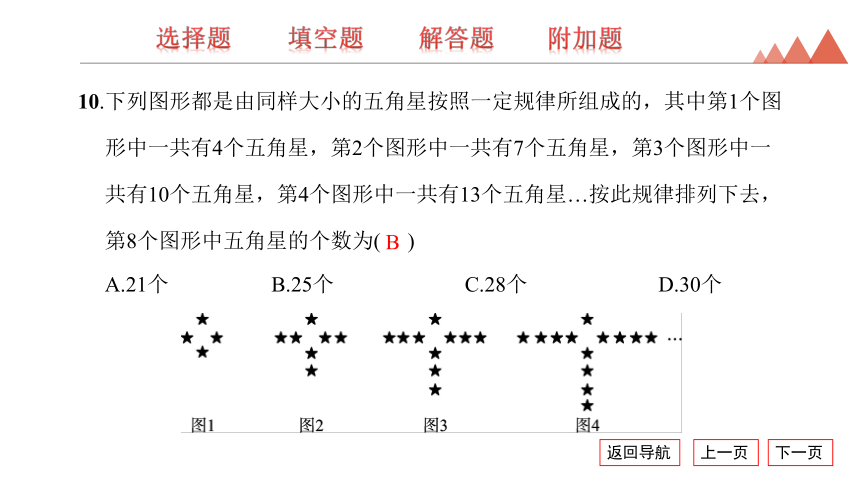
10.下列图形都是由同样大小的五角星按照一定规律所组成的,其中第1个图形中一共有4个五角星,第2个图形中一共有7个五角星,第3个图形中一共有10个五角星,第4个图形中一共有13个五角星…按此规律排列下去,第8个图形中五角星的个数为( )
A.21个 B.25个 C.28个 D.30个
B
二、填空题(每小题3分,共24分)
11.当a=-4,b=1时,式子 的值等于_______.
12.计算:-a-(-a+2a)=_______.
13.已知3x2yn-1是关于x,y的五次单项式,则n=_______.
14.体育委员带了500元钱去买体育用品,已知一个足球a元,一个篮球b元,则式子500-3a-2b表示的意义为__________________________________.
12
-2a
4
买了3个足球和2个篮球后还剩的钱数
15.已知一个多项式与3x2+9x的和等于5x2+4x-1,则这个多项式是_____________________.
16.若a+b=2010,c+d=-5,则式子(a-2c)-(2d-b)=_______.
17.某校计划组织七年级师生去绍兴鲁迅故居研学.若学校租用30座的客车x辆,则有15人无法乘坐;若租用45座的客车,则可少租用2辆,且最后一辆车还没坐满.那么乘坐最后一辆45座客车的人数是______________人.(用含x的式子表示)
2x2-5x-1
2020
(-15x+150)
18.按一定规律排列的一列数依次为:- , ,- , ,…(a≠0),按此规律排列下去,这列数中的第n个数是______________.(n为正整数)
解析:第1个数为 ,第2个数为 ,第3个数为
,第4个数为 ,…所以这列数中的第n个数是
.
三、解答题(共66分)
19.(8分)化简:
(1)2(2a-3b)+3(2b-3a);
(2)4x2-(2x2+x-1)+(2-x2+3x).
解:(1)原式=4a-6b+6b-9a=-5a.
(2)原式=4x2-2x2-x+1+2-x2+3x=x2+2x+3.
20.(10分)先化简,再求值:
(1)(-x2+4x+3)-(3-4x-2x2),其中x=-2;
解:(1)原式=-x2+4x+3-3+4x+2x2=x2+8x,
当x=-2时,原式=(-2)2+8×(-2)=4-16=-12.
(2)-3[b-(3a2-3ab)]-[b+2(4a2-4ab)]-(-a)2,其中a=2,b=-1.
(2)原式=-3b+9a2-9ab-b-8a2+8ab-a2=-4b-ab,
当a=2,b=-1时,原式=4+2=6.
21.(8分)已知-3x2ym+1+x3y-3x4-1是五次四项式,且单项式3x2ny3-m与多项式的次数相同,求m,n的值.
解:因为-3x2ym+1+x3y-3x4-1是五次四项式,
所以2+m+1=5,解得m=2.
因为单项式3x2ny3-m与多项式的次数相同,
所以2n+3-m=5,即2n+3-2=5,解得n=2.
22.(8分)如图是一个长为a,宽为b的长方形,两个阴影图形都是一对底边长为1,且底边在长方形对边上的平行四边形.
(1)用含字母a,b的式子表示长方形中空白部分的面积S;
解:(1)S=ab-a-b+1.
(2)当a=3,b=2时,求长方形中空白部分的面积.
(2)当a=3,b=2时,S=6-3-2+1=2.
23.(8分)某客运中心有两种客车共100辆,其中甲种客车每辆有42个座位,乙种客车有x辆,每辆有22个座位.
(1)乙种客车共有_______个座位,甲种客车共有_____________个座位;
(2)该客运中心的客车共有多少个座位?
22x
(4200-42x)
解:该客运中心的客车共有座位22x+(4200-42x)=(4200-20x)(个).
24.(12分)已知A=ax2-x-1(a为常数),B=3x2-2x+2.
(1)当a= 时,化简B-2A;
解:(1)当a=2(1)时,B-2A=3x2-2x+2-2(ax2-x-1)=(3-2a)x2+4=2x2+4.
(2)在(1)的条件下,若B-2A-2C=0,求C;
(3)若A与B的和中不含x2项,求a的值.
(2)因为B-2A-2C=0,B-2A=2x2+4,
所以2x2+4-2C=0,所以C=x2+2.
(3)A+B=ax2-x-1+3x2-2x+2=(a+3)x2-3x+1,
因为A与B的和中不含x2项,
所以a+3=0,所以a=-3.
25.(12分)某服装厂生产一种夹克和T恤,夹克每件定价200元,T恤每件定价60元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款.现某客户要到该服装厂购买夹克30件、T恤x件(x>30).
(1)若该客户按方案①购买,夹克需付款_______元,T恤需付款______________元(用含x的式子表示);若该客户按方案②购买,夹克需付款_______元,T恤需付款______________元(用含x的式子表示);
6000
60(x-30)
4800
48x
(2)按方案①购买夹克和T恤共需付款______________元(用含x的式子表示),按方案②购买夹克和T恤共需付款______________元(用含x的式子表示);
(4200+60x)
(4800+48x)
(3)若两种优惠方案可同时使用,当x=40时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并说明理由.
解:先按方案①购买夹克30件,再按方案②购买T恤10件更为省钱.理由如下:
当x=40时,按方案①购买所需费用为30×200+60×(40-30)=6600(元),
按方案②购买所需费用为30×200×80%+60×40×80%=6720(元),
先按方案①购买夹克30件所需费用为6000元,
再按方案②购买T恤10件的费用为60×80%×10=480(元),
则总费用为6000+480=6480(元).
因为6720>6600>6480,
所以先按方案①购买夹克30件,再按方案②购买T恤10件的购买方案更省钱.
附加题(10分)
在数学活动课上,同学们利用如图所示的程序进行计算,计算按箭头指向循环进行.如:当初始输入x的值为5,即x=5时,第1次计算的结果为16;第2次计算的结果为8;第3次计算的结果为4…
(1)当初始输入x的值为1时,第1次计算的结果为_______;
(2)当初始输入x的值为4时,第3次计算的结果为_______;
4
4
(3)当初始输入x的值为3时,依次计算得到的所有结果中,有多少个不同的值?求第20次计算的结果.
解:当x=3时,第1次计算的结果为3x+1=10;第2次计算的结果为 =5;第3次计算的结果为3x+1=16;第4次计算的结果为 =8;第5次计算的结果为
=4;第6次计算的结果为 =2;第7次计算的结果为 =1;第8次计算的结果为3x+1=4;…可以发现,从第5次开始,结果都是4,2,1三个数循环,所以一共有7个不同的值.因为(20-4)÷3=5……1,所以第20次计算的结果为4.
测试范围:第二章
选择题
填空题
解答题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
一、选择题(每小题3分,共30分)
1.在式子ab,-6, , , ,- ,m2+2m-1,-p3q中,整式有( )
A.5个 B.6个
C.7个 D.8个
B
2.下列选项中,两个单项式属于同类项的是( )
A.a3与b3 B.3x2y与-4x2yz
C.x2y与-xy2 D.-2a2b与ba2
3.“a与b的平方的和”用式子表示正确的是( )
A.a2+b B.(a+b)2
C.a+b2 D.a2+b2
D
C
4.下列计算结果正确的是( )
A.2x+3y=5xy B.5a2+3a2=8a4
C.3xy-5yx=-2xy D.4a2b-5ab2=-a2b
5.下列去括号正确的是( )
A.x-(-2x2+x3)=x+2x2-x3 B.-(a+b)=-a+b
C.2(a+b)=2a-2b D.-x-(y-z)=-x-y-z
C
A
6.下列说法正确的是( )
A.-3πa2b的系数是-3 B. xy2的次数是2
C.-2x3+3x2-x的次数是6 D.a2-2a-3的常数项是-3
7.某超市一商品的进价为m元,将其价格提高50%作为零售价,半年后又以六折的价格促销,则此时这一商品的价格为( )
A.m元 B.0.9m元
C.0.92m元 D.1.04m元
D
B
8.若a-b=-1,则式子(a-b)2-3a+3b的值是( )
A.4 B.3
C.2 D.-2
9.长方形的一边长是4x+y,另一边比它短x-y,则长方形的周长是( )
A.7x+y B.7x+3y
C.14x+2y D.14x+6y
A
D
10.下列图形都是由同样大小的五角星按照一定规律所组成的,其中第1个图形中一共有4个五角星,第2个图形中一共有7个五角星,第3个图形中一共有10个五角星,第4个图形中一共有13个五角星…按此规律排列下去,第8个图形中五角星的个数为( )
A.21个 B.25个 C.28个 D.30个
B
二、填空题(每小题3分,共24分)
11.当a=-4,b=1时,式子 的值等于_______.
12.计算:-a-(-a+2a)=_______.
13.已知3x2yn-1是关于x,y的五次单项式,则n=_______.
14.体育委员带了500元钱去买体育用品,已知一个足球a元,一个篮球b元,则式子500-3a-2b表示的意义为__________________________________.
12
-2a
4
买了3个足球和2个篮球后还剩的钱数
15.已知一个多项式与3x2+9x的和等于5x2+4x-1,则这个多项式是_____________________.
16.若a+b=2010,c+d=-5,则式子(a-2c)-(2d-b)=_______.
17.某校计划组织七年级师生去绍兴鲁迅故居研学.若学校租用30座的客车x辆,则有15人无法乘坐;若租用45座的客车,则可少租用2辆,且最后一辆车还没坐满.那么乘坐最后一辆45座客车的人数是______________人.(用含x的式子表示)
2x2-5x-1
2020
(-15x+150)
18.按一定规律排列的一列数依次为:- , ,- , ,…(a≠0),按此规律排列下去,这列数中的第n个数是______________.(n为正整数)
解析:第1个数为 ,第2个数为 ,第3个数为
,第4个数为 ,…所以这列数中的第n个数是
.
三、解答题(共66分)
19.(8分)化简:
(1)2(2a-3b)+3(2b-3a);
(2)4x2-(2x2+x-1)+(2-x2+3x).
解:(1)原式=4a-6b+6b-9a=-5a.
(2)原式=4x2-2x2-x+1+2-x2+3x=x2+2x+3.
20.(10分)先化简,再求值:
(1)(-x2+4x+3)-(3-4x-2x2),其中x=-2;
解:(1)原式=-x2+4x+3-3+4x+2x2=x2+8x,
当x=-2时,原式=(-2)2+8×(-2)=4-16=-12.
(2)-3[b-(3a2-3ab)]-[b+2(4a2-4ab)]-(-a)2,其中a=2,b=-1.
(2)原式=-3b+9a2-9ab-b-8a2+8ab-a2=-4b-ab,
当a=2,b=-1时,原式=4+2=6.
21.(8分)已知-3x2ym+1+x3y-3x4-1是五次四项式,且单项式3x2ny3-m与多项式的次数相同,求m,n的值.
解:因为-3x2ym+1+x3y-3x4-1是五次四项式,
所以2+m+1=5,解得m=2.
因为单项式3x2ny3-m与多项式的次数相同,
所以2n+3-m=5,即2n+3-2=5,解得n=2.
22.(8分)如图是一个长为a,宽为b的长方形,两个阴影图形都是一对底边长为1,且底边在长方形对边上的平行四边形.
(1)用含字母a,b的式子表示长方形中空白部分的面积S;
解:(1)S=ab-a-b+1.
(2)当a=3,b=2时,求长方形中空白部分的面积.
(2)当a=3,b=2时,S=6-3-2+1=2.
23.(8分)某客运中心有两种客车共100辆,其中甲种客车每辆有42个座位,乙种客车有x辆,每辆有22个座位.
(1)乙种客车共有_______个座位,甲种客车共有_____________个座位;
(2)该客运中心的客车共有多少个座位?
22x
(4200-42x)
解:该客运中心的客车共有座位22x+(4200-42x)=(4200-20x)(个).
24.(12分)已知A=ax2-x-1(a为常数),B=3x2-2x+2.
(1)当a= 时,化简B-2A;
解:(1)当a=2(1)时,B-2A=3x2-2x+2-2(ax2-x-1)=(3-2a)x2+4=2x2+4.
(2)在(1)的条件下,若B-2A-2C=0,求C;
(3)若A与B的和中不含x2项,求a的值.
(2)因为B-2A-2C=0,B-2A=2x2+4,
所以2x2+4-2C=0,所以C=x2+2.
(3)A+B=ax2-x-1+3x2-2x+2=(a+3)x2-3x+1,
因为A与B的和中不含x2项,
所以a+3=0,所以a=-3.
25.(12分)某服装厂生产一种夹克和T恤,夹克每件定价200元,T恤每件定价60元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款.现某客户要到该服装厂购买夹克30件、T恤x件(x>30).
(1)若该客户按方案①购买,夹克需付款_______元,T恤需付款______________元(用含x的式子表示);若该客户按方案②购买,夹克需付款_______元,T恤需付款______________元(用含x的式子表示);
6000
60(x-30)
4800
48x
(2)按方案①购买夹克和T恤共需付款______________元(用含x的式子表示),按方案②购买夹克和T恤共需付款______________元(用含x的式子表示);
(4200+60x)
(4800+48x)
(3)若两种优惠方案可同时使用,当x=40时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并说明理由.
解:先按方案①购买夹克30件,再按方案②购买T恤10件更为省钱.理由如下:
当x=40时,按方案①购买所需费用为30×200+60×(40-30)=6600(元),
按方案②购买所需费用为30×200×80%+60×40×80%=6720(元),
先按方案①购买夹克30件所需费用为6000元,
再按方案②购买T恤10件的费用为60×80%×10=480(元),
则总费用为6000+480=6480(元).
因为6720>6600>6480,
所以先按方案①购买夹克30件,再按方案②购买T恤10件的购买方案更省钱.
附加题(10分)
在数学活动课上,同学们利用如图所示的程序进行计算,计算按箭头指向循环进行.如:当初始输入x的值为5,即x=5时,第1次计算的结果为16;第2次计算的结果为8;第3次计算的结果为4…
(1)当初始输入x的值为1时,第1次计算的结果为_______;
(2)当初始输入x的值为4时,第3次计算的结果为_______;
4
4
(3)当初始输入x的值为3时,依次计算得到的所有结果中,有多少个不同的值?求第20次计算的结果.
解:当x=3时,第1次计算的结果为3x+1=10;第2次计算的结果为 =5;第3次计算的结果为3x+1=16;第4次计算的结果为 =8;第5次计算的结果为
=4;第6次计算的结果为 =2;第7次计算的结果为 =1;第8次计算的结果为3x+1=4;…可以发现,从第5次开始,结果都是4,2,1三个数循环,所以一共有7个不同的值.因为(20-4)÷3=5……1,所以第20次计算的结果为4.
