22.8多边形的内角和与外角和

(共19张PPT)
知识与技能:
经历探索多边形内角和与外角和公式的过程，进一步发展学生的说理能力和简单的推力能力。
过程与方法:
会应用多边形内角和与外角和公式解决简单问题。
情感态度与价值观:
培养学生良好的合作精神和合作意识，在与人交流的过程中，充分发挥学生的主体性和创造性。
观察与思考：
请你用线把从不同的方向看到的物体轮廓图与下面对应的平面图形连结起来。
在平面内，由三条不在同一直线上的线段首尾顺次相接组成平面图形叫做三角形。
在平面内，由四条不在同一直线上的线段首尾顺次相接组成的平面图形叫做四边形。
在平面内，由5条不在同一直线上的线段首尾顺次相接组成的平面图形叫做五边形。
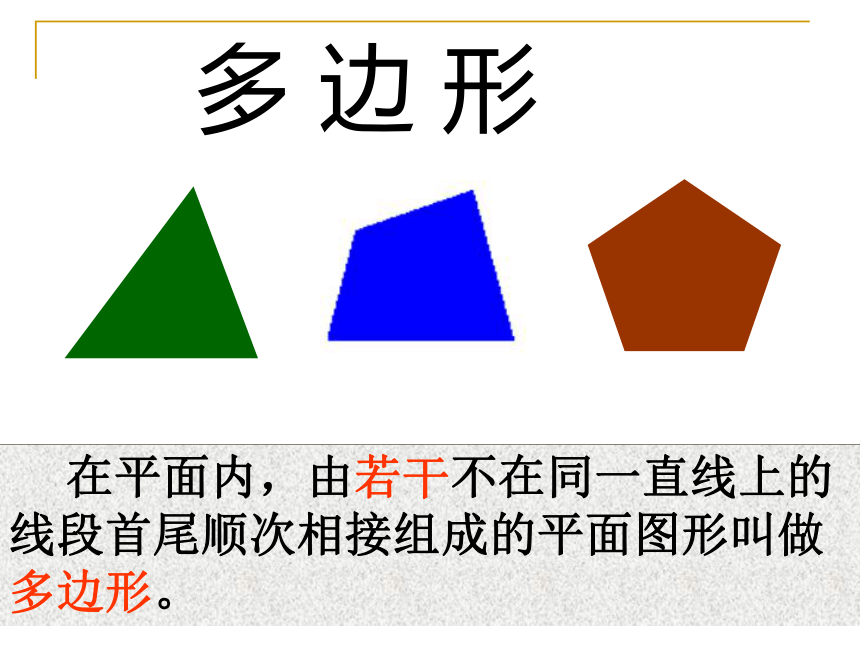
多 边 形
在平面内，由若干不在同一直线上的线段首尾顺次相接组成的平面图形叫做多边形。
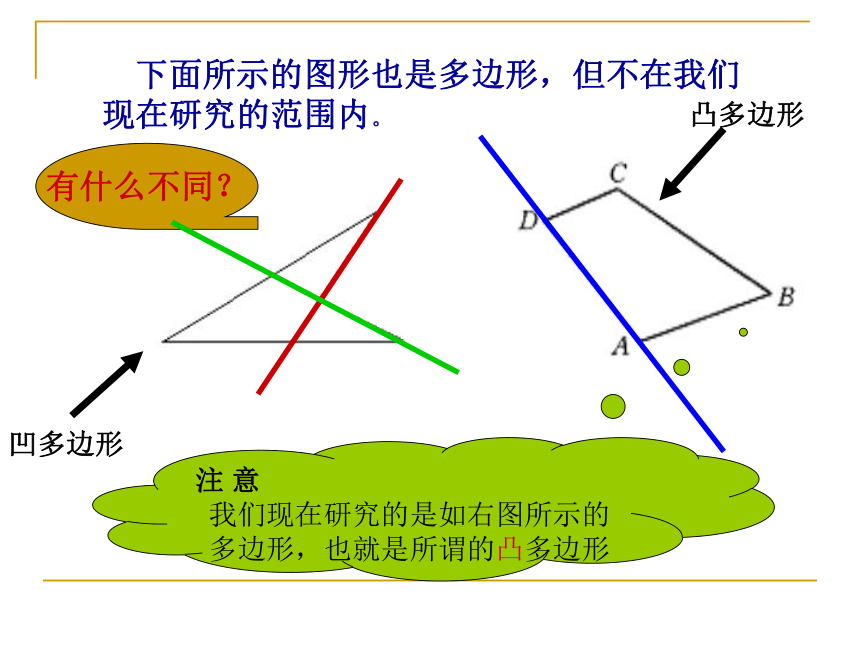
下面所示的图形也是多边形，但不在我们现在研究的范围内。
注 意
我们现在研究的是如右图所示的多边形，也就是所谓的凸多边形
有什么不同？
凹多边形
凸多边形
E
D
C
B
A
顶点
内角
边
外角
对角线
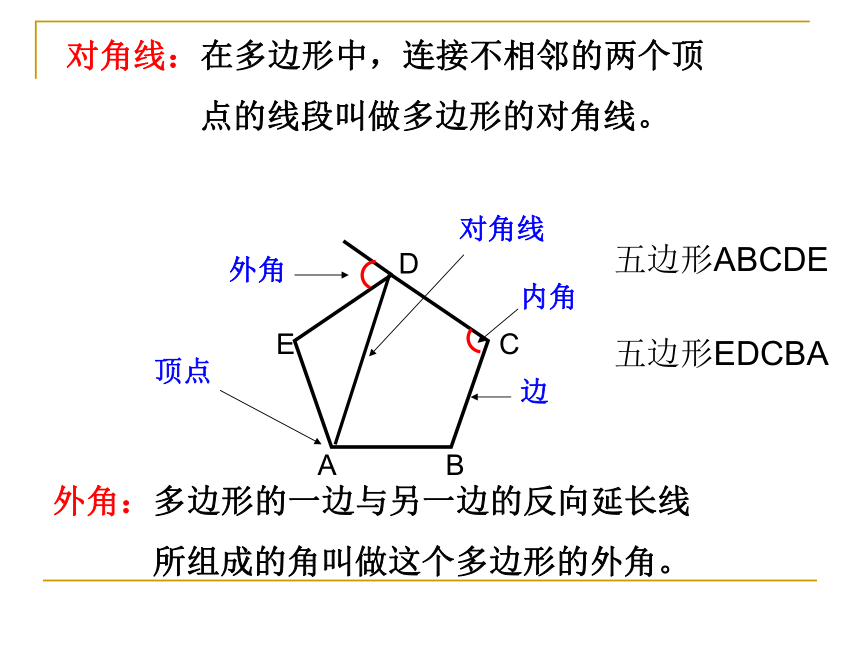
对角线：在多边形中，连接不相邻的两个顶
点的线段叫做多边形的对角线。
外角：多边形的一边与另一边的反向延长线
所组成的角叫做这个多边形的外角。
五边形ABCDE
五边形EDCBA
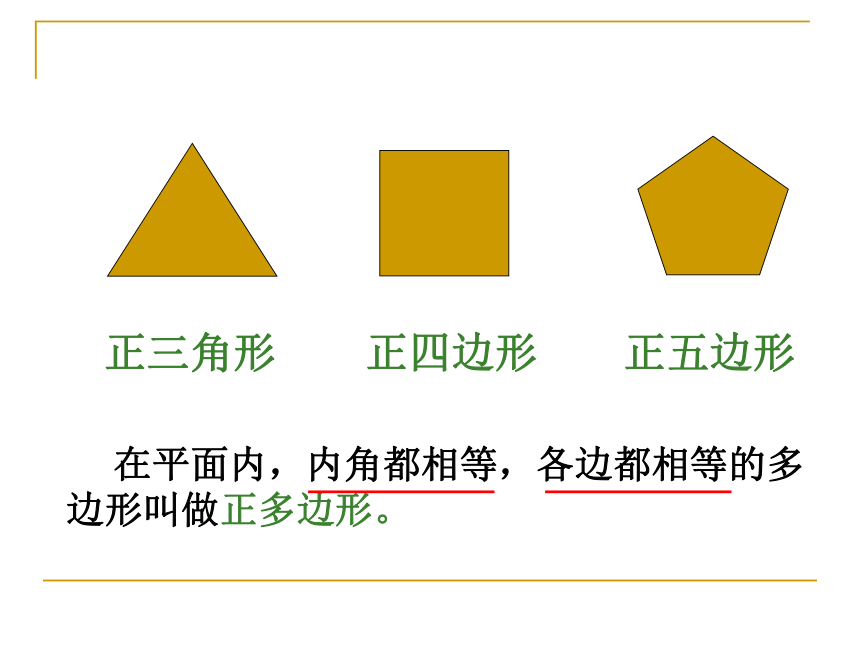
正三角形
正四边形
正五边形
在平面内，内角都相等，各边都相等的多边形叫做正多边形。
大家谈谈
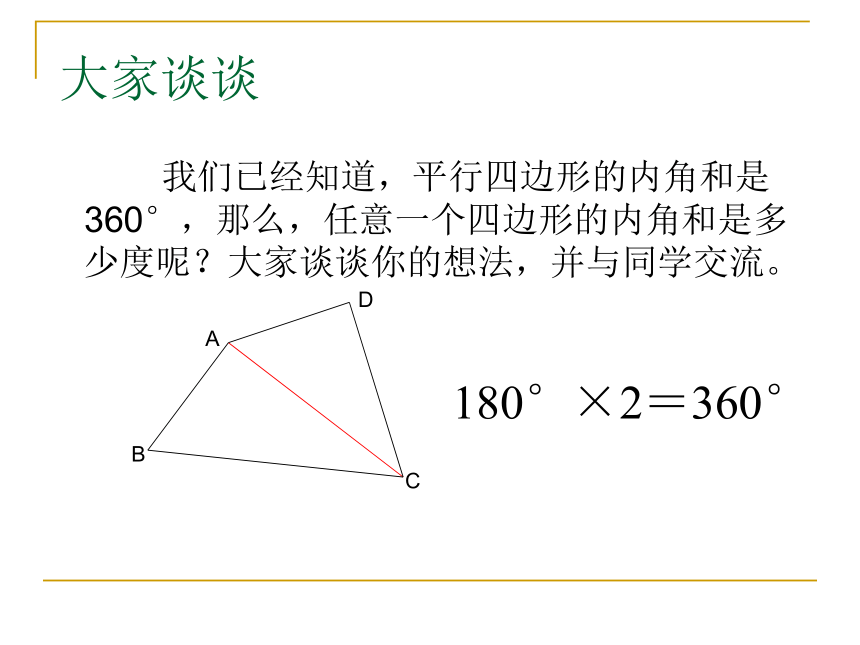
我们已经知道，平行四边形的内角和是360°，那么，任意一个四边形的内角和是多少度呢？大家谈谈你的想法，并与同学交流。
A
B
C
D
180°×2＝360°
我们分析出任意四边形的内角和等于360°所用已知知识是
化未知为已知
那么我们能不能再利用三角形的内角和，来分析五边形的内角和，以及六边形，n边形的内角和？
问题解决过程体现了什么数学思想？
三角形内角和是180度。
探索：五边形的内角和
1 .从顶点A可以画几条对角线？分别是哪几条？
2. 这样五边形被分成了几个三角形？
3. 五边形的内角和是多少度？
A
B
D
C
E
探索六边形的内角和
请你认真地想一想，你能通过怎样的方法把多边形转化为三角形？
A
B
C
D
E
F
被分得三角形个数
六边形的内角和
4
4×180°
这种探索方法你掌握了吗？请完成下表
多边形的边数 3 4 5 6 7 … n
分成的三角形个数 1 2 …
多边形的内角和 180° 360 ° …
3
4
5
n-2
900 °
(n-2) ×180 °
720 °
540 °
n 边形的内角和为：（n－2）×180°
那么对于正多边形来说,会不会出现特殊情况呢？
因为正多边形的每个角相等,所以知道
正多边形的边数,就可以求出每一个内角的度数.
（n－2）×180°/ n
做一做：根据多边形的一个内角与同它相邻的一个外角的和等于180° （互为补角）
图形 边数 内角和与外角和总值 内角和 外角和
3
1×180°
4
5
n边形
2×180°
3×180°
3×180°
4×180°
5×180°
2× 180°
=360°
2× 180°
=360°
2× 180°
=360°
n
n×180°
(n-2)×180°
2× 180°
=360°
例1 已知一个多边形，它的内角和与外角和相等，请说明这个多边形是几边形。
解：设多边形的边数为n，则它的内角和等于（n-2）×180 ，外角和等于360 ，由
（n-2）·180 = 360
解得 n = 4
所以，这个多边形是四边形。
一、填空题
十二边形的内角和是（ ）。
正六边形的一个内角等于（ ）。
一个多边形当边数增加1时，它的内角和增加（ ）。
1800
120
180
二、选择题
1、从 n边形的一个顶点出发作对角线，把这个多边形分
成三角形的个数是（ ）。
A、n B、n-1 C、n-2 D、n-3
2、n边形所有外角的个数是（ ）。
A、n B、2n C、3n D、不能确定
3、一个多边形每个外角都是30 ，这个多边形（ ）。
A、十边形 B、十一边形 C、十二边形 D、十三边形
C
B
C
归纳与总结 ：
一、多边形的内角和等于 (n-2) ×180°
二、多边形的内角和等于 360°
数学解题思想：“化未知为已知 ”
作业：
1.教材P86 习题 第3题
2.探究：请你尝试用其它方法得出多边形内角和公式？
谢 谢！