人教版数学九年级上册24.1.4圆周角 课件(16张)
文档属性
| 名称 | 人教版数学九年级上册24.1.4圆周角 课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 204.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-21 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
24.1圆周角
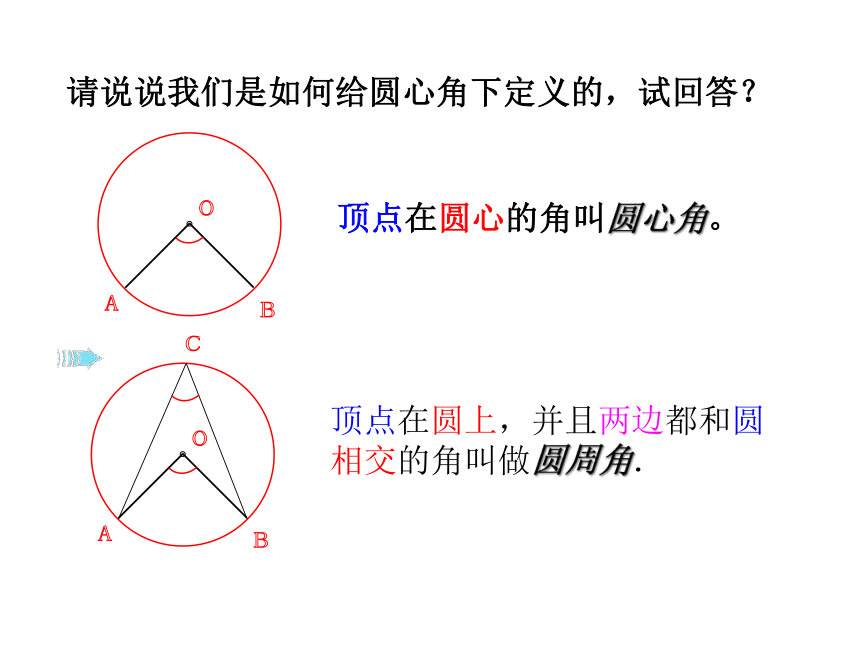
请说说我们是如何给圆心角下定义的,试回答?
o
A
B
顶点在圆心的角叫圆心角。
o
A
B
C
顶点在圆上,并且两边都和圆相交的角叫做圆周角.
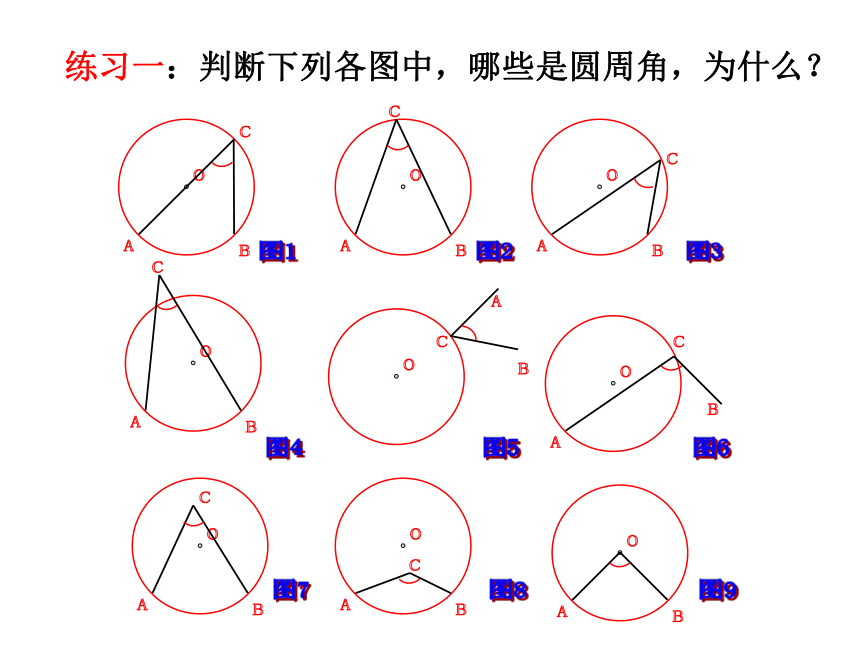
练习一:判断下列各图中,哪些是圆周角,为什么?
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
C
C
C
C
C
C
C
C
图1
图2
图3
图4
图5
图6
图7
图8
图9
探究
·
C
D
A
B
O
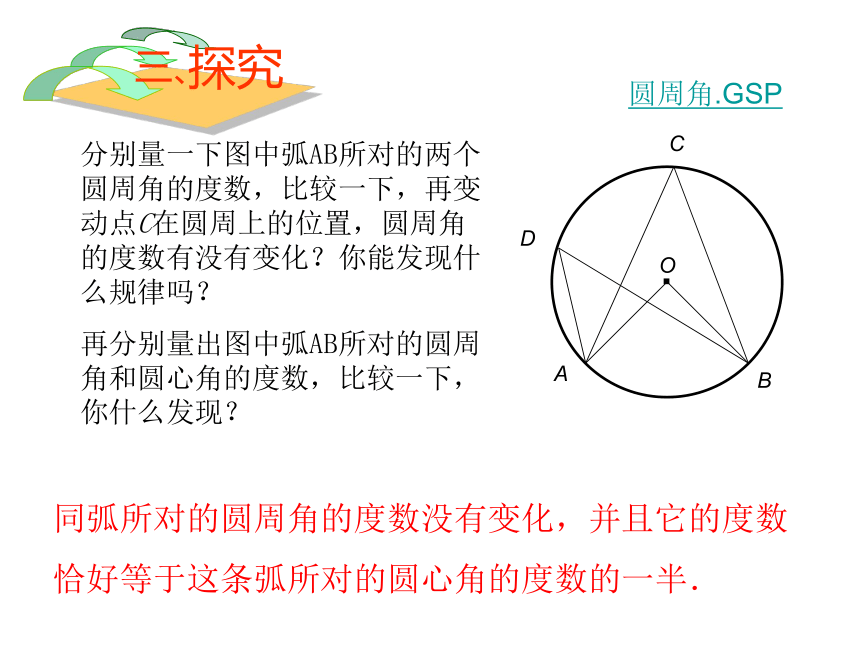
同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半.
三、
分别量一下图中弧AB所对的两个圆周角的度数,比较一下,再变动点C在圆周上的位置,圆周角的度数有没有变化?你能发现什么规律吗?
再分别量出图中弧AB所对的圆周角和圆心角的度数,比较一下,你什么发现?
圆周角.GSP
为了进一步探究上面的发现,如图在⊙O任取一个圆周角∠BAC,将圆对折,使折痕经过圆心O和∠BAC的顶点A.由于点A的位置的取法可能不同,这时折痕可能会:
(1)在圆周角的一条边上;
·
C
O
A
B
四、同弧所对圆周角与圆心角的关系
即
∵OA=OC,
∴∠A=∠C.
又∠BOC=∠A+∠C
∴∠BOC=2∠A
(2)在圆周角的内部.
圆心O在∠BAC的内部,作直径AD,利用(1)的结果,有
·
C
O
A
B
D
(3)在圆周角的外部.
圆心O在∠BAC的外部,作直径AD,利用(1)的结果,有
·
C
O
A
B
D
定理
在同圆或等圆中,同弧或等弧所对的圆
周角相等,都等于这条弧所对的圆心角
的一半.
定
理
·
A
B
C
D
E
O
·
A
B
C1
O
C2
C3
半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
推
论
1.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
A
B
C
D
1
2
3
4
5
6
7
8
∠1
=
∠4
∠5
=
∠8
∠2
=
∠7
∠3
=
∠6
练习
方法点拔:由同弧来找相等的圆周角
2、求圆中角X的度数
B
A
O
.
70°
x
A
O
.
X
120°
练习:
600
B
P
例题
1、在⊙O中,∠CBD=30°
,∠BDC=20°,求∠A
1、在⊙O中,∠CBD=30°
,∠BDC=20°,求∠A
2、如图,在⊙O中,AB为直径,CB
=
CF,
弦CG⊥AB,交AB于D,交BF于E
求证:BE=EC
例题
⌒
⌒
1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
3.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。
2.半圆或直径所对的圆周角都相等,都等于90°
90°的圆周角所对的弦是圆的直径
小结:
谢
谢
24.1圆周角
请说说我们是如何给圆心角下定义的,试回答?
o
A
B
顶点在圆心的角叫圆心角。
o
A
B
C
顶点在圆上,并且两边都和圆相交的角叫做圆周角.
练习一:判断下列各图中,哪些是圆周角,为什么?
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
C
C
C
C
C
C
C
C
图1
图2
图3
图4
图5
图6
图7
图8
图9
探究
·
C
D
A
B
O
同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半.
三、
分别量一下图中弧AB所对的两个圆周角的度数,比较一下,再变动点C在圆周上的位置,圆周角的度数有没有变化?你能发现什么规律吗?
再分别量出图中弧AB所对的圆周角和圆心角的度数,比较一下,你什么发现?
圆周角.GSP
为了进一步探究上面的发现,如图在⊙O任取一个圆周角∠BAC,将圆对折,使折痕经过圆心O和∠BAC的顶点A.由于点A的位置的取法可能不同,这时折痕可能会:
(1)在圆周角的一条边上;
·
C
O
A
B
四、同弧所对圆周角与圆心角的关系
即
∵OA=OC,
∴∠A=∠C.
又∠BOC=∠A+∠C
∴∠BOC=2∠A
(2)在圆周角的内部.
圆心O在∠BAC的内部,作直径AD,利用(1)的结果,有
·
C
O
A
B
D
(3)在圆周角的外部.
圆心O在∠BAC的外部,作直径AD,利用(1)的结果,有
·
C
O
A
B
D
定理
在同圆或等圆中,同弧或等弧所对的圆
周角相等,都等于这条弧所对的圆心角
的一半.
定
理
·
A
B
C
D
E
O
·
A
B
C1
O
C2
C3
半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
推
论
1.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
A
B
C
D
1
2
3
4
5
6
7
8
∠1
=
∠4
∠5
=
∠8
∠2
=
∠7
∠3
=
∠6
练习
方法点拔:由同弧来找相等的圆周角
2、求圆中角X的度数
B
A
O
.
70°
x
A
O
.
X
120°
练习:
600
B
P
例题
1、在⊙O中,∠CBD=30°
,∠BDC=20°,求∠A
1、在⊙O中,∠CBD=30°
,∠BDC=20°,求∠A
2、如图,在⊙O中,AB为直径,CB
=
CF,
弦CG⊥AB,交AB于D,交BF于E
求证:BE=EC
例题
⌒
⌒
1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.
3.在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。
2.半圆或直径所对的圆周角都相等,都等于90°
90°的圆周角所对的弦是圆的直径
小结:
谢
谢
同课章节目录
