人教版 九年级九年级数学 24.2 点和圆、直线和圆的位置关系 突破训练(Word版 含答案)
文档属性
| 名称 | 人教版 九年级九年级数学 24.2 点和圆、直线和圆的位置关系 突破训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 499.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 22:01:11 | ||
图片预览




文档简介
人教版 九年级九年级数学 24.2 点和圆、直线和圆的位置关系 突破训练
一、选择题
1. 下列说法中,正确的是( )
A.垂直于半径的直线是圆的切线
B.经过半径的外端且垂直于这条半径的直线是圆的切线
C.经过半径的端点且垂直于这条半径的直线是圆的切线
D.到圆心的距离等于直径的直线是圆的切线
2. 已知半径为10的⊙O和直线l上一点A,且OA=10,则直线l与⊙O的位置关系是( )
A.相切 B.相交 C.相离 D.相切或相交
3. 2020·武汉模拟 在Rt△ABC中,∠BAC=90°,AB=8,AC=6,以点A为圆心,4.8为半径的圆与直线BC的公共点的个数为( )
A.0 B.1 C.2 D.不能确定
4. 如图,AB为⊙O的切线,切点为A,连接AO,BO,BO与⊙O交于点C,延长BO与⊙O交于点D,连接AD.若∠ABO=36°,则∠ADC的度数为( )
A.54° B.36° C.32° D.27°
5. 在平面直角坐标系中,⊙O的圆心在原点处,半径为2,则下列各点在⊙O上的是( )
A.(1,1) B.(-1,)
C.(-2,-1) D.(2,-2)
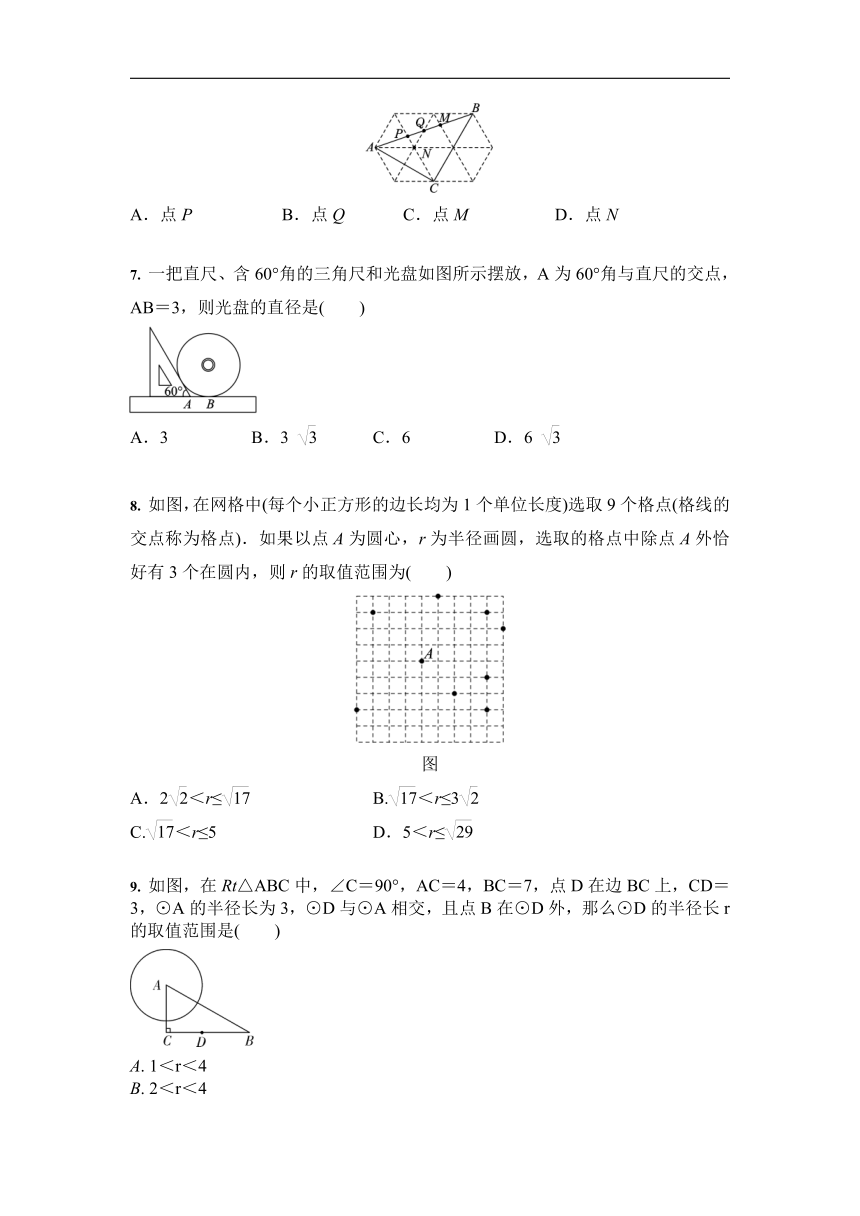
6. 如图,在正三角形网格中,△ABC的顶点都在格点上,点P,Q,M是AB与网格线的交点,则△ABC的外心是( )
A.点P B.点Q C.点M D.点N
7. 一把直尺、含60°角的三角尺和光盘如图所示摆放,A为60°角与直尺的交点,AB=3,则光盘的直径是( )
A.3 B.3 C.6 D.6
8. 如图,在网格中(每个小正方形的边长均为1个单位长度)选取9个格点(格线的交点称为格点).如果以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
图
A.2<r≤ B.<r≤3
C.<r≤5 D.5<r≤
9. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
A. 1<r<4
B. 2<r<4
C. 1<r<8
D. 2<r<8
10. 如图,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在⊙O外、⊙O内、⊙O上,则原点O的位置应该在( )
图
A.点A与点B之间靠近点A
B.点A与点B之间靠近点B
C.点B与点C之间靠近点B
D.点B与点C之间靠近点C
二、填空题
11. 如图,AB是⊙O的直径,O是圆心,BC与⊙O相切于点B,CO交⊙O于点D,且BC=8,CD=4,那么⊙O的半径为________.
12. 如图,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC,垂足为E,要使DE是⊙O的切线,则图中的线段应满足的条件是____________.
13. 如图0,PA,PB分别切⊙O于点A,B,PA=6,CD切⊙O于点E,分别交PA,PB于C,D两点,则△PCD的周长是________.
14. 在周长为26π的⊙O中,CD是⊙O的一条弦,AB是⊙O的切线,且AB∥CD,若AB和CD之间的距离为18,则弦CD的长为________.
15. 如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D.若BD=-1,则∠ACD=________°.
16. 已知l1∥l2,l1,l2之间的距离是3 cm,圆心O到直线l1的距离是1 cm,如果圆O与直线l1,l2有三个公共点,那么圆O的半径为________cm.
17. 在Rt△ABC中,∠C=90°,AC=6,BC=8.若以C为圆心,R为半径所作的圆与斜边AB只有一个公共点,则R的取值范围是______________.
三、解答题
18. 2018·邵阳 如图所示,AB是⊙O的直径,C为⊙O上一点,过点B作BD⊥CD,垂足为D,连接BC,BC平分∠ABD.
求证:CD为⊙O的切线.
19. 如图,在△ABC中,AB=AC,∠BAC=120°,点O在BC上,⊙O经过点A,C,且交BC于点D,直径EF⊥AC于点G.
(1)求证:AB是⊙O的切线;
(2)若AC=8,求BD的长.
20. 如图,AC是⊙O的直径,PA切⊙O于点A,PB切⊙O于点B,且∠APB=60°.
(1)求∠BAC的度数;
(2)若PA=1,求点O到弦AB的距离.
21. 已知:如图,在Rt△ABC中,∠C=90°,AC=8,AB=10.点P在AC上,AP=2.若⊙O的圆心在线段BP上,且⊙O与AB,AC分别切于点D,E.求:
(1)△BAP的面积S;
(2)⊙O的半径.
22. 如图所示,P为正比例函数y=x图象上的一个动点,⊙P的半径为3,设点P的坐标为(x,y).
(1)求⊙P与直线x=2相切时,点P的坐标;
(2)请直接写出⊙P与直线x=2相交、相离时,x的取值范围;
(3)求当原点O在⊙P上时,圆心P的坐标.
人教版 九年级九年级数学 24.2 点和圆、直线和圆的位置关系 突破训练-答案
一、选择题
1. 【答案】B
2. 【答案】D [解析] 若OA⊥l,则圆心O到直线l的距离就是OA的长,等于半径,所以直线l与⊙O相切;
若OA与直线l不垂直,根据垂线段最短,可知圆心O到直线l的距离小于10,即小于半径,所以直线l与⊙O相交.
3. 【答案】B
4. 【答案】D [解析] ∵AB为⊙O的切线,
∴∠OAB=90°.
∵∠ABO=36°,∴∠AOB=90°-∠ABO=54°.
∴∠ADC=∠AOB=27°.故选D.
5. 【答案】B [解析] A项,点(1,1)到圆心的距离是,<2,故在圆内;B项,点(-1,)到圆心的距离为2,2=2,故在圆上;C项,点(-2,-1)到圆心的距离为,>2,故在圆外;D项,点(2,-2)到圆心的距离为2 ,2 >2,故在圆外.
故选B.
6. 【答案】B [解析] 由题意可知∠BCN=60°,∠ACN=30°,∴∠ACB=∠ACN+∠BCN=90°,
∴△ABC是直角三角形,
∴△ABC的外心是斜边AB的中点.
∵Q是AB的中点,
∴△ABC的外心是点Q.
7. 【答案】D [解析] 设光盘的圆心为O,连接OA,OB,则OB⊥AB,∠OAB=×(180°-60°)=60°.
∵AB=3,∴OA=6,OB=3 ,
∴光盘的直径是6 .故选D.
8. 【答案】B [解析] 如图,∵AD=2 ,AE=AF=,AB=3 ,
∴AB>AE=AF>AD,
∴当<r<3 时,以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.
9. 【答案】B 【解析】连接AD,则AD===5,∵⊙A与⊙D相交,∴3-r<5<3+r,解得2<r<8,又∵点B在⊙D外,∴r 解图
10. 【答案】C [解析] 如图.
二、填空题
11. 【答案】6 [解析] 因为BC是⊙O的切线,所以∠OBC=90°.设⊙O的半径为x,则OB=x,OC=x+4.在Rt△OBC中,由勾股定理,得x2+82=(x+4)2,解得x=6.∴⊙O的半径为6.
12. 【答案】BD=CD或AB=AC(答案不唯一)
[解析] (1)连接OD.要使DE是⊙O的切线,结合DE⊥AC,只需OD∥AC,根据O是AB的中点,只需BD=CD即可;
(2)根据(1)中探求的条件,要使BD=CD,则连接AD,由于∠ADB=90°,只需AB=AC,根据等腰三角形的三线合一即可.
13. 【答案】12 [解析] ∵PA,PB分别切⊙O于A,B两点,CD切⊙O于点E,∴PB=PA=6,CA=CE,DB=DE,∴△PCD的周长=PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=12.
14. 【答案】24 【解析】设AB切⊙O于点E,如解图,连接EO并延长交CD于点M,∵C⊙O=26π=2πr,∴r=13,∵AB∥CD,且AB与CD之间的距离为18,∴OM=18-r=5,∵AB为⊙O的切线,∴∠CMO=∠AEO=90°,∴在Rt△CMO中,CM==12,∴CD=2CM=24.
解图
15. 【答案】112.5 [解析] 如图,连接OC.∵CD是⊙O的切线,∴OC⊥CD.∵BD=-1,OA=OB=OC=1,∴OD=,∴CD===1,∴OC=CD,∴∠DOC=45°.∵OA=OC,∴∠OAC=∠OCA,∴∠OCA=∠DOC=22.5°,
∴∠ACD=∠OCA+∠OCD=22.5°+90°=112.5°.
16. 【答案】2或4 [解析] 设圆O的半径为r cm如图①所示,r-1=3,得r=4;如图②所示,r+1=3,得r=2.
17. 【答案】R=4.8或6三、解答题
18. 【答案】
证明:连接OC.∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,∴OC⊥CD,∴CD为⊙O的切线.
19. 【答案】
解:(1)证明:连接OA,如图所示.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∵OA=OC,∴∠OAC=∠C=30°,
∴∠OAB=120°-30°=90°,
即AB⊥OA.
又∵OA是⊙O的半径,
∴AB是⊙O的切线.
(2)∵直径EF⊥AC,
∴AG=CG=AC=4.
∵∠OAC=30°,
∴OG=OA.
在Rt△AOG中,由勾股定理,得OG2+AG2=OA2,∴OG2+42=(2OG)2,
∴OG= ,
∴OA=2OG= .
∵∠OAB=90°,∠B=30°,
∴BO=2OA=2OD,
∴BD=BO-OD=OD=OA= .
20. 【答案】
解:(1)∵PA切⊙O于点A,PB切⊙O于点B,∴PA=PB,∠PAC=90°.
∵∠APB=60°,
∴△APB是等边三角形,∴∠BAP=60°,
∴∠BAC=90°-∠BAP=30°.
(2)过点O作OD⊥AB于点D,如图所示,则AD=BD=AB.
由(1)得△APB是等边三角形,
∴AB=PA=1,∴AD=.
在Rt△AOD中,∵∠BAC=30°,
∴OD=OA.
由勾股定理,得OA2=OD2+AD2,
即(2OD)2=OD2+()2,
∴OD=,即点O到弦AB的距离为.
21. 【答案】
解:(1)∵∠C=90°,AC=8,AB=10,
∴在Rt△ABC中,由勾股定理,得BC=6,
∴△BAP的面积S=AP·BC=×2×6=6.
(2)连接OD,OE,OA.设⊙O的半径为r,
则S△BAP=AB·r+AP·r=6r,
∴6r=6,解得r=1.
故⊙O的半径是1.
22. 【答案】
解:(1)当⊙P在直线x=2的左侧与该直线相切时,
∵圆心P到直线x=2的距离等于半径3,
∴2-x=3,∴x=-1,
此时y=-,P(-1,-).
当⊙P在直线x=2的右侧与该直线相切时,
∵圆心P到直线x=2的距离等于半径3,
∴x-2=3,
∴x=5,此时y=,P(5,).
综上可得,当⊙P与直线x=2相切时,点P的坐标为(-1,-)或(5,).
(2)当-1<x<5时,⊙P与直线x=2相交;
当x<-1或x>5时,⊙P与直线x=2相离.
(3)当点O在⊙P上时,OP=3.
由勾股定理可得(x-0)2+(y-0)2=32.
又∵y=x,∴x1=,x2=-.
代入y=x可得y1=,y2=-.
∴当原点O在⊙P上时,圆心P的坐标为(,)或(-,-).
一、选择题
1. 下列说法中,正确的是( )
A.垂直于半径的直线是圆的切线
B.经过半径的外端且垂直于这条半径的直线是圆的切线
C.经过半径的端点且垂直于这条半径的直线是圆的切线
D.到圆心的距离等于直径的直线是圆的切线
2. 已知半径为10的⊙O和直线l上一点A,且OA=10,则直线l与⊙O的位置关系是( )
A.相切 B.相交 C.相离 D.相切或相交
3. 2020·武汉模拟 在Rt△ABC中,∠BAC=90°,AB=8,AC=6,以点A为圆心,4.8为半径的圆与直线BC的公共点的个数为( )
A.0 B.1 C.2 D.不能确定
4. 如图,AB为⊙O的切线,切点为A,连接AO,BO,BO与⊙O交于点C,延长BO与⊙O交于点D,连接AD.若∠ABO=36°,则∠ADC的度数为( )
A.54° B.36° C.32° D.27°
5. 在平面直角坐标系中,⊙O的圆心在原点处,半径为2,则下列各点在⊙O上的是( )
A.(1,1) B.(-1,)
C.(-2,-1) D.(2,-2)
6. 如图,在正三角形网格中,△ABC的顶点都在格点上,点P,Q,M是AB与网格线的交点,则△ABC的外心是( )
A.点P B.点Q C.点M D.点N
7. 一把直尺、含60°角的三角尺和光盘如图所示摆放,A为60°角与直尺的交点,AB=3,则光盘的直径是( )
A.3 B.3 C.6 D.6
8. 如图,在网格中(每个小正方形的边长均为1个单位长度)选取9个格点(格线的交点称为格点).如果以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
图
A.2<r≤ B.<r≤3
C.<r≤5 D.5<r≤
9. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
A. 1<r<4
B. 2<r<4
C. 1<r<8
D. 2<r<8
10. 如图,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在⊙O外、⊙O内、⊙O上,则原点O的位置应该在( )
图
A.点A与点B之间靠近点A
B.点A与点B之间靠近点B
C.点B与点C之间靠近点B
D.点B与点C之间靠近点C
二、填空题
11. 如图,AB是⊙O的直径,O是圆心,BC与⊙O相切于点B,CO交⊙O于点D,且BC=8,CD=4,那么⊙O的半径为________.
12. 如图,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC,垂足为E,要使DE是⊙O的切线,则图中的线段应满足的条件是____________.
13. 如图0,PA,PB分别切⊙O于点A,B,PA=6,CD切⊙O于点E,分别交PA,PB于C,D两点,则△PCD的周长是________.
14. 在周长为26π的⊙O中,CD是⊙O的一条弦,AB是⊙O的切线,且AB∥CD,若AB和CD之间的距离为18,则弦CD的长为________.
15. 如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D.若BD=-1,则∠ACD=________°.
16. 已知l1∥l2,l1,l2之间的距离是3 cm,圆心O到直线l1的距离是1 cm,如果圆O与直线l1,l2有三个公共点,那么圆O的半径为________cm.
17. 在Rt△ABC中,∠C=90°,AC=6,BC=8.若以C为圆心,R为半径所作的圆与斜边AB只有一个公共点,则R的取值范围是______________.
三、解答题
18. 2018·邵阳 如图所示,AB是⊙O的直径,C为⊙O上一点,过点B作BD⊥CD,垂足为D,连接BC,BC平分∠ABD.
求证:CD为⊙O的切线.
19. 如图,在△ABC中,AB=AC,∠BAC=120°,点O在BC上,⊙O经过点A,C,且交BC于点D,直径EF⊥AC于点G.
(1)求证:AB是⊙O的切线;
(2)若AC=8,求BD的长.
20. 如图,AC是⊙O的直径,PA切⊙O于点A,PB切⊙O于点B,且∠APB=60°.
(1)求∠BAC的度数;
(2)若PA=1,求点O到弦AB的距离.
21. 已知:如图,在Rt△ABC中,∠C=90°,AC=8,AB=10.点P在AC上,AP=2.若⊙O的圆心在线段BP上,且⊙O与AB,AC分别切于点D,E.求:
(1)△BAP的面积S;
(2)⊙O的半径.
22. 如图所示,P为正比例函数y=x图象上的一个动点,⊙P的半径为3,设点P的坐标为(x,y).
(1)求⊙P与直线x=2相切时,点P的坐标;
(2)请直接写出⊙P与直线x=2相交、相离时,x的取值范围;
(3)求当原点O在⊙P上时,圆心P的坐标.
人教版 九年级九年级数学 24.2 点和圆、直线和圆的位置关系 突破训练-答案
一、选择题
1. 【答案】B
2. 【答案】D [解析] 若OA⊥l,则圆心O到直线l的距离就是OA的长,等于半径,所以直线l与⊙O相切;
若OA与直线l不垂直,根据垂线段最短,可知圆心O到直线l的距离小于10,即小于半径,所以直线l与⊙O相交.
3. 【答案】B
4. 【答案】D [解析] ∵AB为⊙O的切线,
∴∠OAB=90°.
∵∠ABO=36°,∴∠AOB=90°-∠ABO=54°.
∴∠ADC=∠AOB=27°.故选D.
5. 【答案】B [解析] A项,点(1,1)到圆心的距离是,<2,故在圆内;B项,点(-1,)到圆心的距离为2,2=2,故在圆上;C项,点(-2,-1)到圆心的距离为,>2,故在圆外;D项,点(2,-2)到圆心的距离为2 ,2 >2,故在圆外.
故选B.
6. 【答案】B [解析] 由题意可知∠BCN=60°,∠ACN=30°,∴∠ACB=∠ACN+∠BCN=90°,
∴△ABC是直角三角形,
∴△ABC的外心是斜边AB的中点.
∵Q是AB的中点,
∴△ABC的外心是点Q.
7. 【答案】D [解析] 设光盘的圆心为O,连接OA,OB,则OB⊥AB,∠OAB=×(180°-60°)=60°.
∵AB=3,∴OA=6,OB=3 ,
∴光盘的直径是6 .故选D.
8. 【答案】B [解析] 如图,∵AD=2 ,AE=AF=,AB=3 ,
∴AB>AE=AF>AD,
∴当<r<3 时,以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.
9. 【答案】B 【解析】连接AD,则AD===5,∵⊙A与⊙D相交,∴3-r<5<3+r,解得2<r<8,又∵点B在⊙D外,∴r
10. 【答案】C [解析] 如图.
二、填空题
11. 【答案】6 [解析] 因为BC是⊙O的切线,所以∠OBC=90°.设⊙O的半径为x,则OB=x,OC=x+4.在Rt△OBC中,由勾股定理,得x2+82=(x+4)2,解得x=6.∴⊙O的半径为6.
12. 【答案】BD=CD或AB=AC(答案不唯一)
[解析] (1)连接OD.要使DE是⊙O的切线,结合DE⊥AC,只需OD∥AC,根据O是AB的中点,只需BD=CD即可;
(2)根据(1)中探求的条件,要使BD=CD,则连接AD,由于∠ADB=90°,只需AB=AC,根据等腰三角形的三线合一即可.
13. 【答案】12 [解析] ∵PA,PB分别切⊙O于A,B两点,CD切⊙O于点E,∴PB=PA=6,CA=CE,DB=DE,∴△PCD的周长=PC+CD+PD=PC+CE+DE+PD=PC+CA+DB+PD=PA+PB=12.
14. 【答案】24 【解析】设AB切⊙O于点E,如解图,连接EO并延长交CD于点M,∵C⊙O=26π=2πr,∴r=13,∵AB∥CD,且AB与CD之间的距离为18,∴OM=18-r=5,∵AB为⊙O的切线,∴∠CMO=∠AEO=90°,∴在Rt△CMO中,CM==12,∴CD=2CM=24.
解图
15. 【答案】112.5 [解析] 如图,连接OC.∵CD是⊙O的切线,∴OC⊥CD.∵BD=-1,OA=OB=OC=1,∴OD=,∴CD===1,∴OC=CD,∴∠DOC=45°.∵OA=OC,∴∠OAC=∠OCA,∴∠OCA=∠DOC=22.5°,
∴∠ACD=∠OCA+∠OCD=22.5°+90°=112.5°.
16. 【答案】2或4 [解析] 设圆O的半径为r cm如图①所示,r-1=3,得r=4;如图②所示,r+1=3,得r=2.
17. 【答案】R=4.8或6
18. 【答案】
证明:连接OC.∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,∴OC⊥CD,∴CD为⊙O的切线.
19. 【答案】
解:(1)证明:连接OA,如图所示.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∵OA=OC,∴∠OAC=∠C=30°,
∴∠OAB=120°-30°=90°,
即AB⊥OA.
又∵OA是⊙O的半径,
∴AB是⊙O的切线.
(2)∵直径EF⊥AC,
∴AG=CG=AC=4.
∵∠OAC=30°,
∴OG=OA.
在Rt△AOG中,由勾股定理,得OG2+AG2=OA2,∴OG2+42=(2OG)2,
∴OG= ,
∴OA=2OG= .
∵∠OAB=90°,∠B=30°,
∴BO=2OA=2OD,
∴BD=BO-OD=OD=OA= .
20. 【答案】
解:(1)∵PA切⊙O于点A,PB切⊙O于点B,∴PA=PB,∠PAC=90°.
∵∠APB=60°,
∴△APB是等边三角形,∴∠BAP=60°,
∴∠BAC=90°-∠BAP=30°.
(2)过点O作OD⊥AB于点D,如图所示,则AD=BD=AB.
由(1)得△APB是等边三角形,
∴AB=PA=1,∴AD=.
在Rt△AOD中,∵∠BAC=30°,
∴OD=OA.
由勾股定理,得OA2=OD2+AD2,
即(2OD)2=OD2+()2,
∴OD=,即点O到弦AB的距离为.
21. 【答案】
解:(1)∵∠C=90°,AC=8,AB=10,
∴在Rt△ABC中,由勾股定理,得BC=6,
∴△BAP的面积S=AP·BC=×2×6=6.
(2)连接OD,OE,OA.设⊙O的半径为r,
则S△BAP=AB·r+AP·r=6r,
∴6r=6,解得r=1.
故⊙O的半径是1.
22. 【答案】
解:(1)当⊙P在直线x=2的左侧与该直线相切时,
∵圆心P到直线x=2的距离等于半径3,
∴2-x=3,∴x=-1,
此时y=-,P(-1,-).
当⊙P在直线x=2的右侧与该直线相切时,
∵圆心P到直线x=2的距离等于半径3,
∴x-2=3,
∴x=5,此时y=,P(5,).
综上可得,当⊙P与直线x=2相切时,点P的坐标为(-1,-)或(5,).
(2)当-1<x<5时,⊙P与直线x=2相交;
当x<-1或x>5时,⊙P与直线x=2相离.
(3)当点O在⊙P上时,OP=3.
由勾股定理可得(x-0)2+(y-0)2=32.
又∵y=x,∴x1=,x2=-.
代入y=x可得y1=,y2=-.
∴当原点O在⊙P上时,圆心P的坐标为(,)或(-,-).
同课章节目录
