人教版八年级数学上册 第十四章 整式的混合运算 学案(含答案)
文档属性
| 名称 | 人教版八年级数学上册 第十四章 整式的混合运算 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 138.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 23:12:04 | ||
图片预览



文档简介
整式的混合运算(习题)
例题示范
例1:先化简再求值:,其中,.
【过程书写】
解:原式
当,时,
原式
例2:若,,则=_______________.
【思路分析】
观察所求式子,根据同底数幂的乘法,,我们需要求出,的值;
观察已知条件,由,,可求出;
代入,求得,即.
例3:若是一个完全平方式,则m=________.
【思路分析】
完全平方公式是由首平方,尾平方,二倍的乘积组成,观察式子结构,首尾两项是平方项.
将,9写成平方的形式,,故应为二倍的乘积.
对比完全平方公式的结构,完全平方公式有两个.
因此,所以.
巩固练习
计算:
①;
②;
③;
④;
⑤.
化简求值:
①,其中a=1,b=2.
②,其中x=2,y=1.
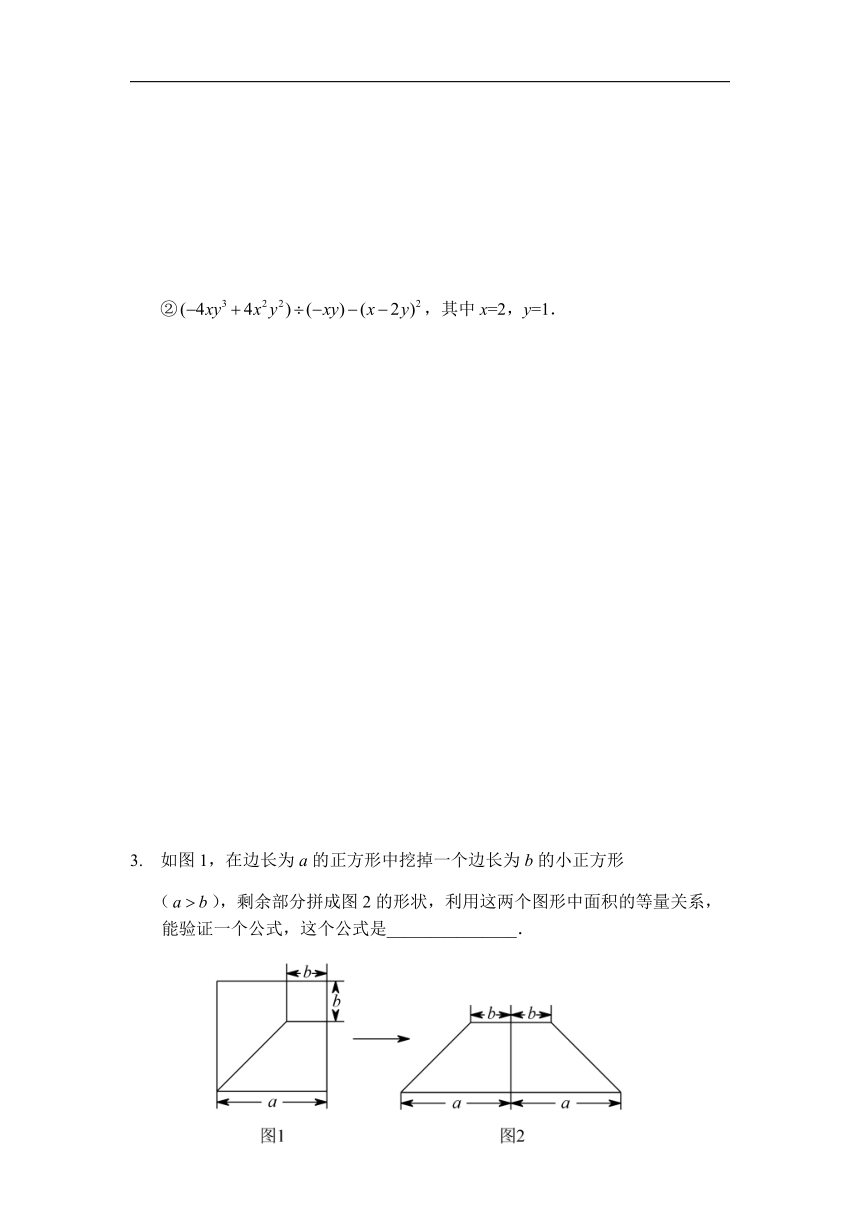
如图1,在边长为a的正方形中挖掉一个边长为b的小正方形
(),剩余部分拼成图2的形状,利用这两个图形中面积的等量关系,能验证一个公式,这个公式是_______________.
若的展开式中不含x2项,则m=_____.
若的展开式中不含x4项,则a=______.
(1)若,则______;若,则______.
(2)若,,则______,______.
(3)若,,则___________.
若,,则________;
若,,则___________.
若,则_____________;
若,则_______.
要使成为一个完全平方式,则m=_____.
要使成为一个完全平方式,则m=_____.
实验表明,人体内某种细胞的形状可近似地看作球,它的直径约为0.000
001
56米,其中0.000
001
56米用科学记数法可表示为___________________米.
思考小结
比较有理数运算与整式运算的异同点:
有理数运算
整式运算
运算法则
有理数加法口诀:
同号相加_________,异号相加_________.
有理数减法法则:
减去一个数等于____
这个数的________.
有理数乘法法则:
两个有理数相乘,同号得___,异号得___,并把______相乘;任何数与0相乘,都得____;几个有理数相乘,因数都不为0时,积的符号由_______的个数决定,当_____为奇数个时积为___,当______为偶数个时积为________,并把
绝对值相乘.
有理数除法法则:
除以一个数等于_____这个数的_______.
幂的运算法则:
加减运算法则:
合并同类项:
系数_____,字母和字母的指数_______.
乘除运算口诀:
单×单:
______乘以______,______乘以______.
单×多:
根据____________,转化为单×单.
多×多:握手原则.
单单:系数除以系数,字母除以字母.
多单:借用乘法分配律.
公式、技巧
①归类组合;
②凑整分解;
③裂项相消;
④倒序相加;
⑤错位相减.
①平方差公式:
_____________________;
②完全平方公式:
_____________________,
_____________________.
【参考答案】
巩固练习
①9a;
②-1;
③-16a4;
④1
275;
⑤4
①0;
②-4
6
(1)4,64
(2)256,16
(3)ab
;8
81;27
思考小结
合并,抵消,加上,相反数,正,负,绝对值,0,负因数,负因数,负,负因数,正,乘以,倒数;
,,,,相加,不变,系数,系数,字母,字母,乘法分配律,,,
例题示范
例1:先化简再求值:,其中,.
【过程书写】
解:原式
当,时,
原式
例2:若,,则=_______________.
【思路分析】
观察所求式子,根据同底数幂的乘法,,我们需要求出,的值;
观察已知条件,由,,可求出;
代入,求得,即.
例3:若是一个完全平方式,则m=________.
【思路分析】
完全平方公式是由首平方,尾平方,二倍的乘积组成,观察式子结构,首尾两项是平方项.
将,9写成平方的形式,,故应为二倍的乘积.
对比完全平方公式的结构,完全平方公式有两个.
因此,所以.
巩固练习
计算:
①;
②;
③;
④;
⑤.
化简求值:
①,其中a=1,b=2.
②,其中x=2,y=1.
如图1,在边长为a的正方形中挖掉一个边长为b的小正方形
(),剩余部分拼成图2的形状,利用这两个图形中面积的等量关系,能验证一个公式,这个公式是_______________.
若的展开式中不含x2项,则m=_____.
若的展开式中不含x4项,则a=______.
(1)若,则______;若,则______.
(2)若,,则______,______.
(3)若,,则___________.
若,,则________;
若,,则___________.
若,则_____________;
若,则_______.
要使成为一个完全平方式,则m=_____.
要使成为一个完全平方式,则m=_____.
实验表明,人体内某种细胞的形状可近似地看作球,它的直径约为0.000
001
56米,其中0.000
001
56米用科学记数法可表示为___________________米.
思考小结
比较有理数运算与整式运算的异同点:
有理数运算
整式运算
运算法则
有理数加法口诀:
同号相加_________,异号相加_________.
有理数减法法则:
减去一个数等于____
这个数的________.
有理数乘法法则:
两个有理数相乘,同号得___,异号得___,并把______相乘;任何数与0相乘,都得____;几个有理数相乘,因数都不为0时,积的符号由_______的个数决定,当_____为奇数个时积为___,当______为偶数个时积为________,并把
绝对值相乘.
有理数除法法则:
除以一个数等于_____这个数的_______.
幂的运算法则:
加减运算法则:
合并同类项:
系数_____,字母和字母的指数_______.
乘除运算口诀:
单×单:
______乘以______,______乘以______.
单×多:
根据____________,转化为单×单.
多×多:握手原则.
单单:系数除以系数,字母除以字母.
多单:借用乘法分配律.
公式、技巧
①归类组合;
②凑整分解;
③裂项相消;
④倒序相加;
⑤错位相减.
①平方差公式:
_____________________;
②完全平方公式:
_____________________,
_____________________.
【参考答案】
巩固练习
①9a;
②-1;
③-16a4;
④1
275;
⑤4
①0;
②-4
6
(1)4,64
(2)256,16
(3)ab
;8
81;27
思考小结
合并,抵消,加上,相反数,正,负,绝对值,0,负因数,负因数,负,负因数,正,乘以,倒数;
,,,,相加,不变,系数,系数,字母,字母,乘法分配律,,,
