苏科版九年级上册数学 2.3 确定圆的条件学案(含答案)
文档属性
| 名称 | 苏科版九年级上册数学 2.3 确定圆的条件学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 99.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 00:00:00 | ||
图片预览


文档简介
确定圆的条件
【知识梳理】
1、条件:不在同一条直线上的三个点确定一个圆。
2、三角形的外接圆:
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆。
外接圆的圆心是三角形的三边的垂直平分线的交点,这个点叫做三角形的外心。这个三角形叫做圆的内接三角形。
3、三角形的外接圆有且只有一个,而圆的内接三角形有无数个。
4、钝角三角形外心在三角形外部、锐角三角形外心在其内部、直角三角形外心在三角形上(在斜边的中点上,且半
径为斜边的一半)
5、三角形的外心的性质:三角形的外心到各个顶点的距离相等
例题训练
例1.经过一点作圆可以作
个圆;经过两点作圆可以作
个圆,这些圆的圆心在这两点的
上;经过
的三点可以作
个圆,并且只能作
个圆。
例2.一个三角形能画
个外接圆,一个圆中有
个内接三角形。
例3.
三角形的外心是三角形的
的圆心,它是三角形的
的交点,它到
的距离相等。
例4.
Rt⊿ABC中,∠C=900,AC=6cm,BC=8cm,则其外接圆的半径为
。
例5.已知AB=7cm,则过点A,B,且半径为3cm的圆有(
)
A
0个
B
1个
C
2个
D
无数个
例6.等边三角形的边长为a,则其外接圆的半径为
.
例7.
如图,平原上有三个村庄A,B,C,现计划打一水井P,使水井到三个村庄的距离相等。在图中画出水井P的位置。
.A
.B
C.
例8.在Rt△ABC中,∠C=90°,若AC=6,BC=8.求Rt△ABC的外接圆的半径和面积。
巩固练习
一、选择题
1.可以作圆,且只可以作一个圆的条件是
(
)
A.已知圆心的位置
B.已知圆的半径大小
C.过三个点
D.过不在同一条直线上的三个点
2.三角形的外心是
(
)
A.三条边高的交点
B.三个角的平分线的交点
C.三边垂直平分线的交点
D.三边中线的交点
3.A、B、C是平面内的三点,AB=3,BC=3,AC=6,下列说法正确的是
(
)
A.可以画一个圆,使A、B、C都在圆上
B.可以画一个圆,使A、B在圆上,C在圆外
C.可以画一个圆,使A、C在圆上,B在圆外
D.可以画一个圆,使B、C在圆上,A在圆内
4.△ABC内接于☉O,OD
AC于点D,如果COD=600,那么B的度数为
(
)
A.
300
B.600
C.600或1200
D.300或1500
二、填空题
5.三角形的外心是_______的圆心,它是________的交点,它到______的距离相等.
6.△ABC是直径为10
cm的⊙O的内接等腰三角形,如果此等腰三角形的底边BC=8
cm,则△ABC的面积为_______.
7.如图,以点P为圆心的圆弧与x轴交于A,B两点,点P的坐标为(4,2),点A的坐标为(2,0),则点B的坐标为________.
第7题
8.如图,在平面直角坐标系中,已知一圆弧过正方形网格的格点A、B、C,已知A点的坐标为(-3,5),则该圆弧所在圆的圆心坐标为________.
三、解答题
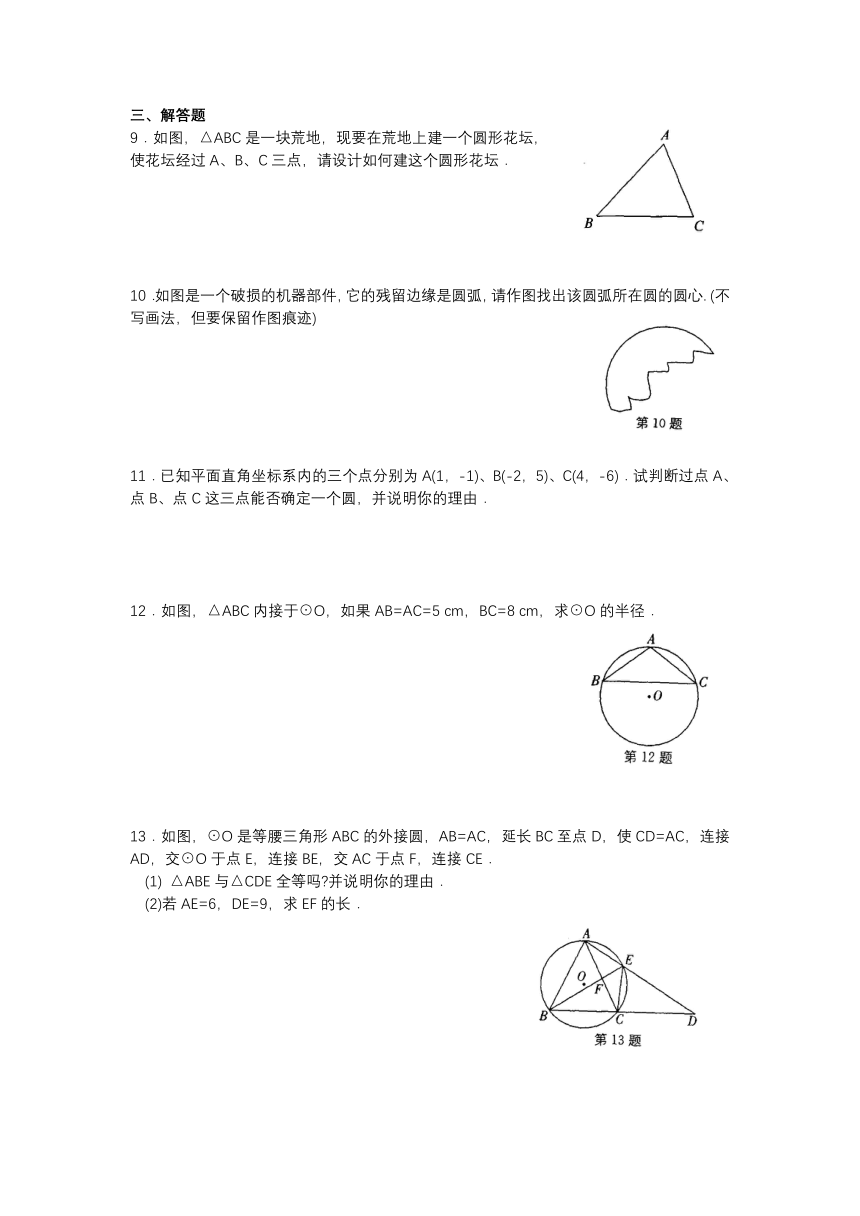
9.如图,△ABC是一块荒地,现要在荒地上建一个圆形花坛,
使花坛经过A、B、C三点,请设计如何建这个圆形花坛.
10.如图是一个破损的机器部件,它的残留边缘是圆弧,请作图找出该圆弧所在圆的圆心.
(不写画法,但要保留作图痕迹)
11.已知平面直角坐标系内的三个点分别为A(1,-1)、B(-2,5)、C(4,-6).试判断过点A、点B、点C这三点能否确定一个圆,并说明你的理由.
12.如图,△ABC内接于☉O,如果AB=AC=5
cm,BC=8
cm,求☉O的半径.
13.如图,☉O是等腰三角形ABC的外接圆,AB=AC,延长BC至点D,使CD=AC,连接AD,交☉O于点E,连接BE,交AC于点F,连接CE.
(1)
△ABE与△CDE全等吗?并说明你的理由.
(2)若AE=6,DE=9,求EF的长.
14.如图,△ABC是等边三角形,D是弧BC上任一点,请判断BD、CD和DA间的关系.
15.(2010.绍兴)如图,⊙O是正三角形ABC的外接圆,点P在劣弧AB上,∠ABP=22°,则∠BCP的度数为______.
巩固练习答案:
1.D
2.C
3.B
4.C
5.其外接圆
三边垂直平分线-三角形三个顶点
6.8
cm2或
32
cm2
7.(6,0)
8.(-l,0)
9.作出△ABC的外接圆即为圆形花坛,图略.
10.如图所示点拨:过圆弧上任意三点作两条不同的弦,再分别作出这两条弦的垂直平分线,且相交于点O.
则点O即为该圆弧所在圆的圆心
11.设过点A、点B的直线解析式为y=kx+b,
A(1,-1)、B(-2.5),
解得.
即y=-2x+1.
当x=4时,y=-7≠-6,点C不在直线AB上.
即点A、点B、点C这三点不在同一直线上.
过点A、点B、点C这三点能确定一个圆
12.☉O的半径为cm
13.(1)全等
四边形ABCE内接于☉O,
DEC=
ABC,DCE=
BAE.
AB=AC.
ABC=
ACB.
又
ACB=
AEB,CD=AC,AEB=
ABC,AB=CD.
AEB=
CED.
△ABE
△CDE
(2)由△ABE
△CDE
,得
ABE=D,BE=DE=9.
又CD=AC,
CAD=D.CAD=ABE.
又AEF=BEA,
△AFE≌△BAE.
又BE=9,AE=6,
EF=4
14.
DB+CD=DA.
15.38
【知识梳理】
1、条件:不在同一条直线上的三个点确定一个圆。
2、三角形的外接圆:
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆。
外接圆的圆心是三角形的三边的垂直平分线的交点,这个点叫做三角形的外心。这个三角形叫做圆的内接三角形。
3、三角形的外接圆有且只有一个,而圆的内接三角形有无数个。
4、钝角三角形外心在三角形外部、锐角三角形外心在其内部、直角三角形外心在三角形上(在斜边的中点上,且半
径为斜边的一半)
5、三角形的外心的性质:三角形的外心到各个顶点的距离相等
例题训练
例1.经过一点作圆可以作
个圆;经过两点作圆可以作
个圆,这些圆的圆心在这两点的
上;经过
的三点可以作
个圆,并且只能作
个圆。
例2.一个三角形能画
个外接圆,一个圆中有
个内接三角形。
例3.
三角形的外心是三角形的
的圆心,它是三角形的
的交点,它到
的距离相等。
例4.
Rt⊿ABC中,∠C=900,AC=6cm,BC=8cm,则其外接圆的半径为
。
例5.已知AB=7cm,则过点A,B,且半径为3cm的圆有(
)
A
0个
B
1个
C
2个
D
无数个
例6.等边三角形的边长为a,则其外接圆的半径为
.
例7.
如图,平原上有三个村庄A,B,C,现计划打一水井P,使水井到三个村庄的距离相等。在图中画出水井P的位置。
.A
.B
C.
例8.在Rt△ABC中,∠C=90°,若AC=6,BC=8.求Rt△ABC的外接圆的半径和面积。
巩固练习
一、选择题
1.可以作圆,且只可以作一个圆的条件是
(
)
A.已知圆心的位置
B.已知圆的半径大小
C.过三个点
D.过不在同一条直线上的三个点
2.三角形的外心是
(
)
A.三条边高的交点
B.三个角的平分线的交点
C.三边垂直平分线的交点
D.三边中线的交点
3.A、B、C是平面内的三点,AB=3,BC=3,AC=6,下列说法正确的是
(
)
A.可以画一个圆,使A、B、C都在圆上
B.可以画一个圆,使A、B在圆上,C在圆外
C.可以画一个圆,使A、C在圆上,B在圆外
D.可以画一个圆,使B、C在圆上,A在圆内
4.△ABC内接于☉O,OD
AC于点D,如果COD=600,那么B的度数为
(
)
A.
300
B.600
C.600或1200
D.300或1500
二、填空题
5.三角形的外心是_______的圆心,它是________的交点,它到______的距离相等.
6.△ABC是直径为10
cm的⊙O的内接等腰三角形,如果此等腰三角形的底边BC=8
cm,则△ABC的面积为_______.
7.如图,以点P为圆心的圆弧与x轴交于A,B两点,点P的坐标为(4,2),点A的坐标为(2,0),则点B的坐标为________.
第7题
8.如图,在平面直角坐标系中,已知一圆弧过正方形网格的格点A、B、C,已知A点的坐标为(-3,5),则该圆弧所在圆的圆心坐标为________.
三、解答题
9.如图,△ABC是一块荒地,现要在荒地上建一个圆形花坛,
使花坛经过A、B、C三点,请设计如何建这个圆形花坛.
10.如图是一个破损的机器部件,它的残留边缘是圆弧,请作图找出该圆弧所在圆的圆心.
(不写画法,但要保留作图痕迹)
11.已知平面直角坐标系内的三个点分别为A(1,-1)、B(-2,5)、C(4,-6).试判断过点A、点B、点C这三点能否确定一个圆,并说明你的理由.
12.如图,△ABC内接于☉O,如果AB=AC=5
cm,BC=8
cm,求☉O的半径.
13.如图,☉O是等腰三角形ABC的外接圆,AB=AC,延长BC至点D,使CD=AC,连接AD,交☉O于点E,连接BE,交AC于点F,连接CE.
(1)
△ABE与△CDE全等吗?并说明你的理由.
(2)若AE=6,DE=9,求EF的长.
14.如图,△ABC是等边三角形,D是弧BC上任一点,请判断BD、CD和DA间的关系.
15.(2010.绍兴)如图,⊙O是正三角形ABC的外接圆,点P在劣弧AB上,∠ABP=22°,则∠BCP的度数为______.
巩固练习答案:
1.D
2.C
3.B
4.C
5.其外接圆
三边垂直平分线-三角形三个顶点
6.8
cm2或
32
cm2
7.(6,0)
8.(-l,0)
9.作出△ABC的外接圆即为圆形花坛,图略.
10.如图所示点拨:过圆弧上任意三点作两条不同的弦,再分别作出这两条弦的垂直平分线,且相交于点O.
则点O即为该圆弧所在圆的圆心
11.设过点A、点B的直线解析式为y=kx+b,
A(1,-1)、B(-2.5),
解得.
即y=-2x+1.
当x=4时,y=-7≠-6,点C不在直线AB上.
即点A、点B、点C这三点不在同一直线上.
过点A、点B、点C这三点能确定一个圆
12.☉O的半径为cm
13.(1)全等
四边形ABCE内接于☉O,
DEC=
ABC,DCE=
BAE.
AB=AC.
ABC=
ACB.
又
ACB=
AEB,CD=AC,AEB=
ABC,AB=CD.
AEB=
CED.
△ABE
△CDE
(2)由△ABE
△CDE
,得
ABE=D,BE=DE=9.
又CD=AC,
CAD=D.CAD=ABE.
又AEF=BEA,
△AFE≌△BAE.
又BE=9,AE=6,
EF=4
14.
DB+CD=DA.
15.38
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
