人教版 八年级数学上册13.1 轴对称 突破训练(Word版 含答案)
文档属性
| 名称 | 人教版 八年级数学上册13.1 轴对称 突破训练(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 442.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-20 00:00:00 | ||
图片预览



文档简介
人教版
八年级数学13.1
轴对称
突破训练
一、选择题
1.
方程=3的解是( )
A.
-
B.
C.
-4
D.
4
2.
小明用15元买售价相同的软面笔记本,小丽用24元买售价相同的硬面笔记本(两人的钱恰好用完),已知每本硬面笔记本比软面笔记本贵3元,且小明和小丽买到相同数量的笔记本.设软面笔记本每本售价为x元,根据题意可列出的方程为
( )
A.=
B.=
C.=
D.=
3.
如图,已知直线MN是线段AB的垂直平分线,垂足为N,AM=5
cm,△MAB的周长为16
cm,那么AN的长为
( )
A.3
cm
B.4
cm
C.5
cm
D.6
cm
4.
分式方程+=1的解为( )
A.x=-1
B.x=1
C.x=2
D.x=-2
5.
若方程+=6的解是x=2,则m的值为( )
A.2
B.-2
C.2.4
D.-2.4
6.
如图,DE是△ABC中AB边的垂直平分线,若BC=6,AC=8,则△BCE的周长为( )
A.10
B.12
C.14
D.16
7.
如图,△ABC和△AB′C′关于直线l对称,下列结论中,错误的是( )
A.△ABC≌△AB′C′
B.∠BAC′=∠B′AC
C.l垂直平分点C,C′的连线
D.直线BC和B′C′的交点不在直线l上
8.
对于△ABC,嘉淇用尺规进行如下操作:
如图,(1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点D;
(2)作直线AD交BC边于点E.
根据嘉淇的操作方法,可知线段AE是( )
A.△ABC的高线
B.△ABC的中线
C.边BC的垂直平分线
D.△ABC的角平分线
9.
图中序号(1)(2)(3)(4)对应的四个三角形都是由△ABC进行了一次变换之后得到的,其中是通过轴对称变换得到的是
( )
A.(1)
B.(2)
C.(3)
D.(4)
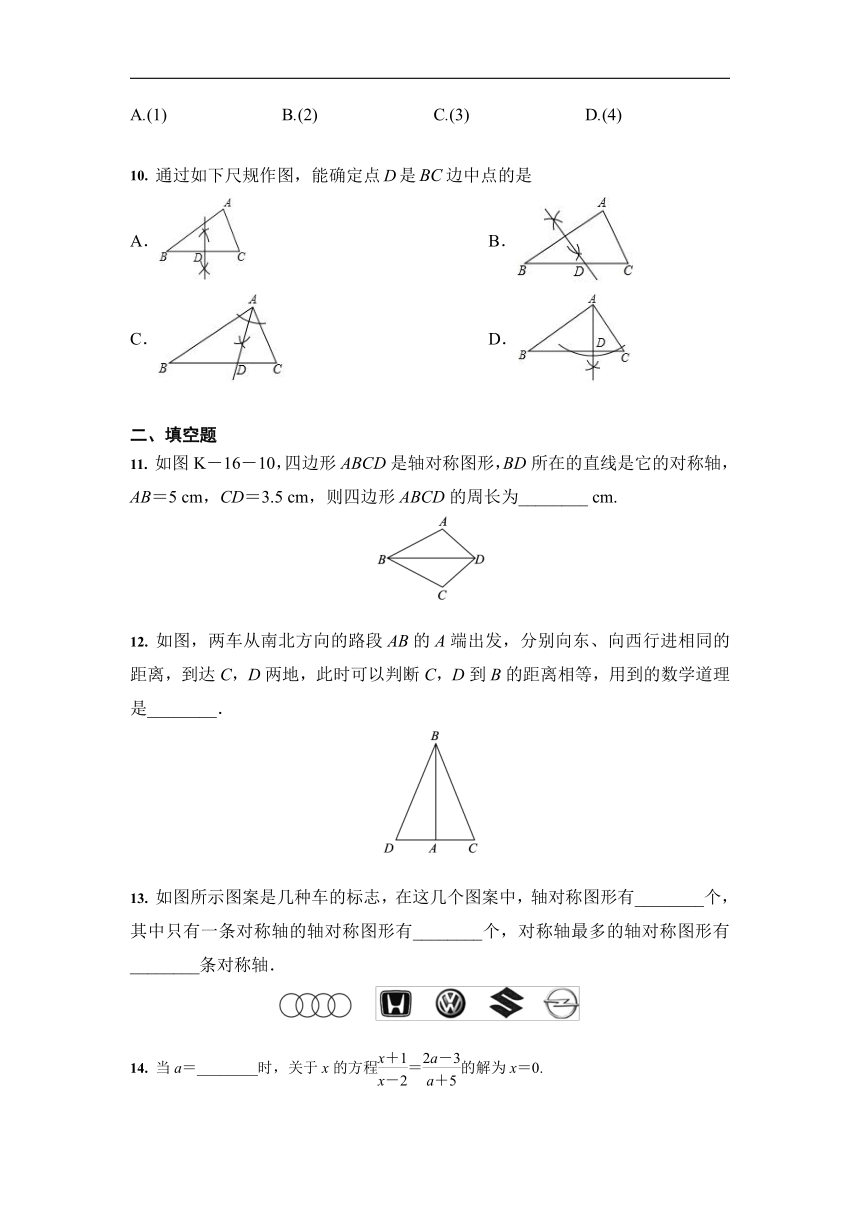
10.
通过如下尺规作图,能确定点是边中点的是
A.
B.
C.
D.
二、填空题
11.
如图K-16-10,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=5
cm,CD=3.5
cm,则四边形ABCD的周长为________
cm.
12.
如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地,此时可以判断C,D到B的距离相等,用到的数学道理是________.
13.
如图所示图案是几种车的标志,在这几个图案中,轴对称图形有________个,其中只有一条对称轴的轴对称图形有________个,对称轴最多的轴对称图形有________条对称轴.
14.
当a=________时,关于x的方程=的解为x=0.
15.
如图,点P在∠AOB内,M,N分别是点P关于OA,OB的对称点,连接MN交OA于点E,交OB于点F.若△PEF的周长是20
cm,则MN的长是________cm.
16.
当a=________时,关于x的方程-=1的解与方程=3的解相同.
三、解答题
17.
如图,在四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A.求证:点A在线段CD的垂直平分线上.
18.
阅读材料,并完成下列问题:
观察分析下列方程:
①x+=3,②x+=5,③x+=7.
由①,得方程的解为x=1或x=2,
由②,得方程的解为x=2或x=3,
由③,得方程的解为x=3或x=4.
(1)观察上述方程及其解,可猜想关于x的方程x+=a+的解为 ;?
(2)请利用你猜想的结论,解关于x的方程=a+.
19.
某企业有九个生产车间,现在每个车间原有的成品一样多,每个车间每天生产的成品也一样多,有A,B两组检验员,其中A组有8名检验员.他们先用两天将第一、二两个车间的成品检验完毕后,再去检验第三、四两个车间的所有成品,又用去了三天时间;同时,用这五天时间,B组检验员也检验完余下的五个车间的成品.如果每名检验员的检验速度一样快,每个车间原有的成品为a件,每个车间每天生产b件成品.
(1)用含a,b的式子表示B组检验员检验的成品总数;
(2)求B组检验员的人数.
20.
整体换元法阅读下列材料,回答问题:
方程-=-的解为x=1;
方程-=-的解为x=2;
方程-=-的解为x=3;
……
(1)请你观察上述方程及其解的特征,写出能反映上述方程一般规律的方程,并写出这个方程的解;
(2)根据(1)中所得的结论,写出一个解为x=-5的分式方程.
人教版
八年级数学13.1
轴对称
突破训练-答案
一、选择题
1.
【答案】D 【解析】本题考查解分式方程,原方程两边同时乘以x-1,得2x+1=3(x-1),解得x=4,把x=4代入x-1=3≠0,所以x=4是原分式方程的根.
2.
【答案】A [解析]本题考查了由实际问题抽象出分式方程,正确找出等量关系是解题关键.直接利用“小明和小丽买到相同数量的笔记本”,得=,故选A.
3.
【答案】A
4.
【答案】A [解析]
方程两边同时乘x(x-1),得x(x-5)+2(x-1)=x(x-1).
解得x=-1.
当x=-1时,x(x-1)≠0,
故x=-1是原方程的解.
5.
【答案】C
6.
【答案】C [解析]
∵DE是△ABC中AB边的垂直平分线,∴AE=BE.∵BC=6,AC=8,∴△BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC=14.
7.
【答案】D
8.
【答案】A
9.
【答案】A
10.
【答案】A
【解析】作线段的垂直平分线可得线段的中点.
由此可知:选项A符合条件,故选A.
二、填空题
11.
【答案】17
12.
【答案】线段垂直平分线上的点与这条线段两个端点的距离相等
13.
【答案】3 2 2
14.
【答案】±1 [解析]
去分母,得x-a=a(x+1).
整理,得(a-1)x=-2a.
当a=1时,0·x=-2,该方程无解.
当a≠1时,x=-.若x=-1,则原分式方程无解,此时-1=-,解得a=-1.
综上可知,当a=±1时原分式方程无解.
故答案为±1.
15.
【答案】20
16.
【答案】解:(1)方程两边同乘(9x-3),
得2(3x-1)+3x=1.解得x=.
检验:当x=时,9x-3=0,
所以x=不是原方程的解.
所以原分式方程无解.
(2)方程两边同乘(x-1)(x+2),
得x(x-1)=2(x+2)+(x-1)(x+2).
解得x=-.
检验:当x=-时,(x-1)(x+2)≠0.
所以原分式方程的解为x=-.
(3)方程两边同乘x(x+1)(x-1),得
三、解答题
17.
【答案】
证明:连接AC.
∵点A在线段BC的垂直平分线MN上,
∴AB=AC.
∵AB=AD,∴AC=AD.
∴点
A在线段CD的垂直平分线上.
18.
【答案】
解:(1)x=a或x=
(2)=a+,
则=a+,
即x+=a+,
变形为(x-1)+=(a-1)+,
所以x-1=a-1或x-1=,
解得x=a或x=.
19.
【答案】
解:(1)B组检验员检验的成品总数为(5a+25b)件.
(2)∵每名检验员的检验速度一样,
∴=,
解得a=4b.
即每名检验员的速度为==b.
B组检验员的人数为==12.
答:B组检验员的人数为12人.
20.
【答案】
解:(1)分式方程中的四个分母都可看作是未知数与一个整数的差,这四个整数左边两个连续,右边两个连续,左右两边不连续,但只间隔一个整数,每个分式的分子都是1,方程的解正好是中间被省略的那个整数,
即-=-,方程的解是x=n(n为整数).
(2)将n=-5代入上式,可得所求分式方程为
-=-.
八年级数学13.1
轴对称
突破训练
一、选择题
1.
方程=3的解是( )
A.
-
B.
C.
-4
D.
4
2.
小明用15元买售价相同的软面笔记本,小丽用24元买售价相同的硬面笔记本(两人的钱恰好用完),已知每本硬面笔记本比软面笔记本贵3元,且小明和小丽买到相同数量的笔记本.设软面笔记本每本售价为x元,根据题意可列出的方程为
( )
A.=
B.=
C.=
D.=
3.
如图,已知直线MN是线段AB的垂直平分线,垂足为N,AM=5
cm,△MAB的周长为16
cm,那么AN的长为
( )
A.3
cm
B.4
cm
C.5
cm
D.6
cm
4.
分式方程+=1的解为( )
A.x=-1
B.x=1
C.x=2
D.x=-2
5.
若方程+=6的解是x=2,则m的值为( )
A.2
B.-2
C.2.4
D.-2.4
6.
如图,DE是△ABC中AB边的垂直平分线,若BC=6,AC=8,则△BCE的周长为( )
A.10
B.12
C.14
D.16
7.
如图,△ABC和△AB′C′关于直线l对称,下列结论中,错误的是( )
A.△ABC≌△AB′C′
B.∠BAC′=∠B′AC
C.l垂直平分点C,C′的连线
D.直线BC和B′C′的交点不在直线l上
8.
对于△ABC,嘉淇用尺规进行如下操作:
如图,(1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点D;
(2)作直线AD交BC边于点E.
根据嘉淇的操作方法,可知线段AE是( )
A.△ABC的高线
B.△ABC的中线
C.边BC的垂直平分线
D.△ABC的角平分线
9.
图中序号(1)(2)(3)(4)对应的四个三角形都是由△ABC进行了一次变换之后得到的,其中是通过轴对称变换得到的是
( )
A.(1)
B.(2)
C.(3)
D.(4)
10.
通过如下尺规作图,能确定点是边中点的是
A.
B.
C.
D.
二、填空题
11.
如图K-16-10,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=5
cm,CD=3.5
cm,则四边形ABCD的周长为________
cm.
12.
如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地,此时可以判断C,D到B的距离相等,用到的数学道理是________.
13.
如图所示图案是几种车的标志,在这几个图案中,轴对称图形有________个,其中只有一条对称轴的轴对称图形有________个,对称轴最多的轴对称图形有________条对称轴.
14.
当a=________时,关于x的方程=的解为x=0.
15.
如图,点P在∠AOB内,M,N分别是点P关于OA,OB的对称点,连接MN交OA于点E,交OB于点F.若△PEF的周长是20
cm,则MN的长是________cm.
16.
当a=________时,关于x的方程-=1的解与方程=3的解相同.
三、解答题
17.
如图,在四边形ABCD中,AB=AD,BC边的垂直平分线MN经过点A.求证:点A在线段CD的垂直平分线上.
18.
阅读材料,并完成下列问题:
观察分析下列方程:
①x+=3,②x+=5,③x+=7.
由①,得方程的解为x=1或x=2,
由②,得方程的解为x=2或x=3,
由③,得方程的解为x=3或x=4.
(1)观察上述方程及其解,可猜想关于x的方程x+=a+的解为 ;?
(2)请利用你猜想的结论,解关于x的方程=a+.
19.
某企业有九个生产车间,现在每个车间原有的成品一样多,每个车间每天生产的成品也一样多,有A,B两组检验员,其中A组有8名检验员.他们先用两天将第一、二两个车间的成品检验完毕后,再去检验第三、四两个车间的所有成品,又用去了三天时间;同时,用这五天时间,B组检验员也检验完余下的五个车间的成品.如果每名检验员的检验速度一样快,每个车间原有的成品为a件,每个车间每天生产b件成品.
(1)用含a,b的式子表示B组检验员检验的成品总数;
(2)求B组检验员的人数.
20.
整体换元法阅读下列材料,回答问题:
方程-=-的解为x=1;
方程-=-的解为x=2;
方程-=-的解为x=3;
……
(1)请你观察上述方程及其解的特征,写出能反映上述方程一般规律的方程,并写出这个方程的解;
(2)根据(1)中所得的结论,写出一个解为x=-5的分式方程.
人教版
八年级数学13.1
轴对称
突破训练-答案
一、选择题
1.
【答案】D 【解析】本题考查解分式方程,原方程两边同时乘以x-1,得2x+1=3(x-1),解得x=4,把x=4代入x-1=3≠0,所以x=4是原分式方程的根.
2.
【答案】A [解析]本题考查了由实际问题抽象出分式方程,正确找出等量关系是解题关键.直接利用“小明和小丽买到相同数量的笔记本”,得=,故选A.
3.
【答案】A
4.
【答案】A [解析]
方程两边同时乘x(x-1),得x(x-5)+2(x-1)=x(x-1).
解得x=-1.
当x=-1时,x(x-1)≠0,
故x=-1是原方程的解.
5.
【答案】C
6.
【答案】C [解析]
∵DE是△ABC中AB边的垂直平分线,∴AE=BE.∵BC=6,AC=8,∴△BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC=14.
7.
【答案】D
8.
【答案】A
9.
【答案】A
10.
【答案】A
【解析】作线段的垂直平分线可得线段的中点.
由此可知:选项A符合条件,故选A.
二、填空题
11.
【答案】17
12.
【答案】线段垂直平分线上的点与这条线段两个端点的距离相等
13.
【答案】3 2 2
14.
【答案】±1 [解析]
去分母,得x-a=a(x+1).
整理,得(a-1)x=-2a.
当a=1时,0·x=-2,该方程无解.
当a≠1时,x=-.若x=-1,则原分式方程无解,此时-1=-,解得a=-1.
综上可知,当a=±1时原分式方程无解.
故答案为±1.
15.
【答案】20
16.
【答案】解:(1)方程两边同乘(9x-3),
得2(3x-1)+3x=1.解得x=.
检验:当x=时,9x-3=0,
所以x=不是原方程的解.
所以原分式方程无解.
(2)方程两边同乘(x-1)(x+2),
得x(x-1)=2(x+2)+(x-1)(x+2).
解得x=-.
检验:当x=-时,(x-1)(x+2)≠0.
所以原分式方程的解为x=-.
(3)方程两边同乘x(x+1)(x-1),得
三、解答题
17.
【答案】
证明:连接AC.
∵点A在线段BC的垂直平分线MN上,
∴AB=AC.
∵AB=AD,∴AC=AD.
∴点
A在线段CD的垂直平分线上.
18.
【答案】
解:(1)x=a或x=
(2)=a+,
则=a+,
即x+=a+,
变形为(x-1)+=(a-1)+,
所以x-1=a-1或x-1=,
解得x=a或x=.
19.
【答案】
解:(1)B组检验员检验的成品总数为(5a+25b)件.
(2)∵每名检验员的检验速度一样,
∴=,
解得a=4b.
即每名检验员的速度为==b.
B组检验员的人数为==12.
答:B组检验员的人数为12人.
20.
【答案】
解:(1)分式方程中的四个分母都可看作是未知数与一个整数的差,这四个整数左边两个连续,右边两个连续,左右两边不连续,但只间隔一个整数,每个分式的分子都是1,方程的解正好是中间被省略的那个整数,
即-=-,方程的解是x=n(n为整数).
(2)将n=-5代入上式,可得所求分式方程为
-=-.
